- Учителю
- Урок математики в 11 классе по теме 'Показательная функция'
Урок математики в 11 классе по теме 'Показательная функция'
Открытый урок по математике в 11 классе
Тема: «Показательная функция»
Учитель математики Кузьмина Н.А.
2014
МОКУ Малиновская СОШ отделение №2
20.11.2014
«Да, путь познания не гладок!
Но знаем мы со школьных лет
Загадок больше, чем отгадок
И поискам предела нет!»
Пифагор (2 слайд)
Тема: «Показательная функция»
Цели:
- образовательные
-
обеспечить в начале урока определение обучающимися темы урока;
-
сформулировать определение показательной функции;
-
построить ее график;
-
по графику определить свойства показательной функции;
-
вывести алгоритм решения показательных уравнений;
-
научить применять алгоритм при решении показательных уравнений;
-
осуществить контроль и взаимоконтроль знаний учащихся, и их коррекцию.
- воспитательные
-
воспитывать навыки культуры труда;
-
воспитывать эстетический вкус;
-
в целях подготовки к выпускному государственному экзамену, использовать материалы демоверсий ЕГЭ по математике.
- развивающие
-
развивать чувство ответственности и навыки самостоятельного труда и взаимоконтроля;
-
развивать логическое мышление;
-
вырабатывать умение прогнозировать, классифицировать и обобщать;
-
продолжить развивать умение читать свойства функции по графику.
Тип урока: урок открытия новых знаний
Методы: наглядный, словесный, графический, условно-символический, комментируемое управление с места
Оборудование, наглядность: ноутбук, слайдовая презентация (36 слайдов), плакат с формулами по теме «Свойства степеней», классная доска, учебник «Алгебра и начала анализа» под редакцией Колмогорова А. Н., сборник материалов ЕГЭ математика, практикум авторов Л.Д. Лаппо, М.А. Попов изд. «Экзамен» Москва 2014г, чертёжные инструменты.
Формы организации учебной деятельности: индивидуальная, фронтальная, диалог, работа с текстом слайда, с учебником.
Учебный предмет: математика
Уровень образования школьников: 10 классов
Форма учебной работы: классно-урочная
Используемые технологии:
Информационно - коммуникационная
Элементы проблемного обучения
Идеи технологии С.Н. Лысенковой «опережающее обучение при комментируемом управлении с места»
Межпредметные связи:
-
С историей (презентация)
-
С физикой (презентация)
-
С биологией (презентация)
План урока
-
Организационно-психологический момент
-
Актуализация знаний
-
Историческая справка
-
Изучение теоретического материала
-
Закрепление теоретического материала
-
Самостоятельная работа
-
Коррекция знаний
-
Подведение итогов урока. Рефлексия
-
Домашнее задание
-
Определение перспективы на следующие уроки
Ход урока:
-
Организационно-психологический момент. Мотивация
(Цель этапа: включение учащихся в учебную деятельность)
Приветствует обучающихся, создает эмоциональный настрой на урок. Сегодня мы начинаем изучать новую тему, название которой вы определите в процессе нашей совместной работы.
-
Актуализация знаний и фиксирование затруднения в пробном действии (Цель этапа: актуализация знаний, повторение ранее изученного материала, обсуждение незнакомой ситуации)
Ответьте на вопросы: (3 слайд)
1.Как называется выражение ar ?
2. В этом выражении а - это …?, r - это …?
3.Дать определение степени числа а > 0 с рациональным показателем r .
Устно: (4 слайд)
1.Назовите основания степеней: (1/22)5 и 74
2.Назовите показатели степеней: 5 и 32
3.Вычислите: 52; 23; (1/3)2; 4-2; 7-2;(1/3)-3
4.Представьте число в виде степени: 49; 16; 1/5; 1/9
5. Представьте число 81 в виде степени с разными основаниями
Вывод: эти знания и умения необходимы вам как для изучения новой темы, так и для подготовки к ЕГЭ.
Звучат сообщения 2-х учащихся - «Исторические сведения о степенях»:
-
Истоки понятия степени находятся в глубокой древности. Дошедшие до нас глиняные плитки древних вавилонян содержат записи таблиц квадратов, кубов и их обратных значений. (5 слайд)
-
В Древнем Вавилоне математика зародилась задолго до нашей эры. Вавилоняне умели решать уравнения второй степени и некоторые виды уравнений третьей степени при помощью специальных таблиц. (6 слайд)
-
Дробные показатели степени и наиболее простые правила действий над степенями с дробными показателями ввел в 14 веке французский епископ города Лизье в Нормандии Николай Орезм (1323 -1382гг). (7 слайд)
-
В 15 веке француз Никола Шюке (1445-1500гг.) в работе «Наука о числах в трех книгах» рассматривал степени с отрицательными и нулевыми показателями. (8 сл)
-
Немецкий математик Михаэль Штифель (1486-1567гг.) ввел название «показатели» (exponenten) и дал определение а0=1, при а≠0. (9 слайд)
-
Способы записи степеней менялись с течением времени, и только французский ученый Рене Декарт в своей «Геометрии» ввел современные обозначения степени, за исключением второй степени, которую он записывал как произведение двух множителей (А×А вместо А2). (10 слайд)
-
Завершили введение современного изображения степени англичане Джон Валлис и Исаак Ньютон в 17 веке. (11 слайд)
Работа с обучающимися по определению темы урока.
-
Ответьте на вопросы. (12 слайд)
-
Что это у = хn ? А это что у = ах?
Необходимо определить сходство и отличие этих функций!
На основании вывода назовите тему урока!
«Современная математика как раскидистый дуб, раскинула такие могучие ветви, что ни один математик, даже «самый маститый» уже не в силах изучить всю математику, а лишь избирает какую-нибудь ее ветвь» Маркушевич А.И.
А мы с вами сегодня избрали такую «ветвь», как ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ! (13 слайд)
Называется тема урока «Показательная функция» и записывается в тетради. (14 слайд)
-
Выявление места и причины затруднения
(Цель этапа: осознание учащимися того, в чем именно состоит недостаточность их знаний)
-
Построение проекта выхода из затруднения
(Цель этапа: постановка целей урока, выбор способа и средств их реализации)
Работа с обучающимися по определению целей урока: (15 слайд)
-
Дать определение показательной функции
-
Познакомиться с ее графиком
-
С помощью графика определить ее свойства
-
Вывести алгоритм решения показательных уравнений
-
Закрепить знания на практике
-
Реализация построенного проекта и решение исходной задачи
(Цель этапа: построение учащимися нового знания и формирование умений его применять при решении задач)
Итак, попробуйте сформулировать определение показательной функции.
(учащиеся отвечают, учитель, если нужно корректирует определение).
(На слайде появляется определение, учащиеся дополняют нго недостающими элементами)
- Добавить недостающие моменты в определение функции: (16 слайд) Функция, заданная формулой у = ах, где …, называется показательной функцией с основанием …
Возможные варианты:
-
а) а - любое число; б) а > 0; в) а < 0; г) а > 0, а ≠ 1
-
1) х; 2) а; 3) у.
На экране (17 слайд) появляются графики функций, совместно с учащимися определяются их особенности , по графикам (которые демонстрируются) учащиеся определяют свойства функции. Ученики делают чертеж в тетрадях.

Свойства показательной функции: (18 слайд)
-
D(y) =R
-
E(y) = (0;∞)
-
При а>1 функция возрастает; при
0<a<1 - убывает
-
Непрерывная
-
При любых действительных значениях х и у:
ахay = ax+y ; ах/ay = ax-y; (ах)y = axy ; ( ab)x = axbx; ( a/b)x = ax/bx.
Сравните свойства показательной функции и свойства степеней с рациональным показателем (плакат). Вывод: они одинаковы.
Определить и обосновать поведение функции по заданной формуле:(19 слайд) (1 и 2 примеры с записью в тетрадях и на доске, 3 и 4 - устно)
-
у = 4х (возрастает, т.к. а=4>1); у = (0,2)х (убывает, т.к. а = 0,2<1) ;
-
у = ( 1/3)х (убывает, т.к. а = 0,2<1); у = (1,7)х (возрастает, т.к. а = 1,7>1).
Практическое применение показательной функции: Показательная функция имеет важное значение в науке и технике. Многие явления природы можно выразить посредством показательной функции. Например, процесс распада радиоактивного вещества (радий, радон, уран), охлаждение тела, изменение атмосферного давления с изменением высоты, рост колонии живых организмов и др.
-
Процесс распада радиоактивного вещества (20-21 слайды)
Закон поглощения света при прохождении его в глубине рек, озер, морей, океанов; через пластины из различных материалов (исследование глубин, промышленное производство)
-
Закон поглощения света (22 слайд)
-
Изучение поведения морских животных (23слайд)
Переход к новой теме осуществляется через проблемную ситуацию, которая возникает при решении уравнения, которое обучающимся еще не известен.
Задание: (24 слайд)
Решите уравнения (устно): 1) х5 = 32 (Решение: х = 5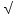 32 Ответ: 2)
32 Ответ: 2)
2)2х = 32
Не можете? Почему? Предложите план решения (АЛГОРИТМ)
(2х = 25; х=5 Ответ: 5)
АЛГОРИТМ РЕШЕНИЯ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ: (25 слайд)
-
ЛЕВУЮ И ПРАВУЮ ЧАСТИ ПОКАЗАТЕЛЬНОГО УРАВНЕНИЯ ПРИВЕСТИ К СТЕПЕНЯМ С ОДИНАКОВЫМ ОСНОВАНИЕМ;
-
ОПУСТИТЬ ОСНОВАНИЯ И ПРИРАВНЯТЬ ПОКАЗАТЕЛИ СТЕПЕНЕЙ;
-
РЕШИТЬ ПОЛУЧЕННОЕ УРАВНЕНИЕ
-
Первичное закрепление с проговариванием во внешней речи
(Цель этапа: усвоение учащимися нового способа действий)
Решите уравнения: (учащиеся работают у доски) (26 слайд)
-
5х = 25
Решение: 5х = 52
х = 2
Ответ: 2
-
25х = 1/5
Решение: 52х = 5-1
2х = -1
х = - 1/2
Ответ: - ½
-
Учебник Стр. 231 № 460 (а,б) Решите уравнения: (при комментируемом управлении с места) (27 слайд)
а) 4х = 64; (ответ: 3) б) (1/3)х = 27 (ответ: -3)
Я предлагаю вам выполнить некоторые задания ЕГЭ по теме нашего урока. (Материалы сборника ЕГЭ по математике, практикум, авторы Л.Д.Лаппо, М.А.Попов, 2014г) (у доски)
-
Стр. 20 Вариант 3 Задание В5
Решите уравнение: 35х-1 = 27 (5х-1=3; 5х=4; х=0,8)
-
Стр.23 Вариант 4 Задание В5
Решите уравнение: (¼)1-2х = 64 (2х-1 = 3; 2х=4; х=2)
Физминутка (гимнастика для глаз) (28-29 слайд)
-
Самостоятельная работа с взаимопроверкой по эталону(30 слайд)
(Цель этапа: обеспечение усвоения алгоритма решения показательного уравнения)
I вариант
1) решить уравнения: 3х = 9
2) 2х+1 = 4
3) определить поведение функции у = (1,3)х
II вариант
1) решить уравнения: 2х = 16
-
3х-1 = 9
-
определить поведение функции у = (0,98)х
-
Эталон решения: (31 слайд)
I вариант
1) 3х = 9 Решение: 3х = 32 х = 2 Ответ: 2
2) 2х+1 = 4 Решение: 2х+1 = 22 х+1 = 2 х = 1 Ответ: 1
-
Функция возрастает, т.к. основание а = 1,3 > 1.
II вариант
1) 2х = 16 Решение: 2х = 24 х = 4 Ответ: 4
2) 3х-1 = 9 Решение: 3х-1 = 32 х-1 = 2 х = 1 Ответ: 1
3) Функция убывает, т.к. основание а = 0,98 < 1.
8. Коррекция знаний (индивидуально)
Желающие могут исправить свои результаты на следующем уроке или на консультации.
9. Подведение итогов урока. Выставление оценок за урок.
Какова была тема урока? Какие цели ставили? Что нового узнали? Существуют ли другие методы решения показательных уравнений?
Все ли из заданных уравнений можно решить по алгоритму? Ответ обоснуйте!(32сл)
-
5-х = 1/25 (да)
-
6х = 36 (да)
-
3х+2 - 3х+1 + 3х = 21 (нет)
-
22х + 3.2х - 80= 0 (нет)
10. Рефлексия учебной деятельности на уроке (Цель этапа: самооценка учащимися результатов своей учебной деятельности) (33 слайд)
1.На уроке я работал(а) активно/ пассивно
2.Своей работой на уроке я доволен/недоволен
3.Урок для меня показался коротким/длинным/нормальным
4.За урок я устал/не устал
5.Мое настроение стало лучше/ стало хуже/ не изменилось
6.Материал урока мне был понятен / не понятен
полезен / бесполезен
интересен / скучен
легким / трудным
10. Домашнее задание (34 слайд) п. 35, № 460 (в,г), 462(а,б) Выучить определение, уметь строить график функции, знать свойства функции, алгоритм решения уравнений .
И наш урок я хочу закончить такими словами: (35-36 слайды)
Да, надо математику любить
И не считать ученье за мученье!
Все в жизни пригодиться, ты учись,
Учись и не жалей на то мгновенья!
Спасибо за урок!