Конспект урока геометрии №9 на тему: Прямоугольник (по учебнику Атанасян Л.С., 8 класс)

Урок 9 ПРЯМОУГОЛЬНИК.

Цели: дать определение прямоугольника, изучить свойства прямоугольника.

Ход урока

I. Проверка домашнего задания.

1. Ответить на вопросы учащихся.АВС - равнобедренный.

ВАС = ВСА = х°,

ВСА = DАС = х°, как внутренние накрест лежащие при ВС || АD и секущей АС, ВАD = СDА = 2х°.

Из прямоугольного АСD САD + СDА = 90°, х + 2х = 90°, х = 30°.

В трапеции А = D = 60°, В = С = 120°.

2. Выполнить задания (устно):

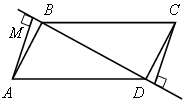
1) Найдите углы выпуклого четырехугольника, если их градусные меры пропорциональны числам 1, 2, 3, 4.2) Докажите, что расстояния АМ и СN от вершин А и С параллелограмма АВСD до прямой ВD равны.

3) Найдите углы параллелограмма АВСD, если А = 3В.

II. Изучение нового материала. учебник стр. 108-109

1. Определение прямоугольника.

2. Так как прямоугольник - параллелограмм, то какими свойствами он обладает?

3. Каким особенным свойством обладает прямоугольник?

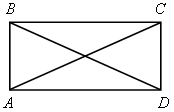
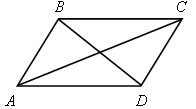
4. Доказательство теоремы о равенстве диагоналей прямоугольника.

5. Будет ли верно обратное утверждение? Докажите.

6. В параллелограмме АВСD А = 90°. Докажите, что АВСD - прямоугольник.

7. АС - диагональ прямоугольника АВСD, САD = 35°. Чему равен АСD?

8. Определите периметр прямоугольника, если две его стороны 5 см и 8 см.

9. АВСD - прямоугольник. Докажите, что АОВ равнобедренный.

III. Решение задач. № 400.

1. В прямоугольнике АВСD биссектриса угла D пересекает сторону АВ в точке М.

1) Докажите, что АDМ - равнобедренный.

2) Найдите периметр прямоугольника, если сторона АВ оказалась разбита на отрезки длиной 3 см и 5 см. Сколько решений имеет задача?

Решение

АD = 3, Р_АВСD = 22 АD = 5, Р_АВСD = 26

IV. Итоги урока.

Свойства прямоугольника

Любой прямоугольник является параллелограммом, значит, обладает всеми его свойствами:

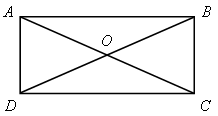
АВСD -

прямоугольник

АВ || CD, ВC || АD,

АВ = СD, ВС = АD,

АО = ОС, ВО = ОD

Кроме того, у прямоугольника имеются свои свойства:

Признаки прямоугольника

АВСD - параллелограмм А = В = C = D = 90°

АВСD - прямоугольник

АВСD - параллелограмм и АС = ВD

АВСD - прямоугольник

Д/з: вопросы 12, 13, с. 115; задачи №№ 403, 413 (а), 401 (а).

Доказать признак прямоугольника: четырехугольник, у которого есть три прямых угла, является прямоугольником.