- Учителю
- Урок- консультация по математике для 11 класса «Решение задач на сплавы, смеси»
Урок- консультация по математике для 11 класса «Решение задач на сплавы, смеси»
Акмолинская область
Зерендинский район
Зерендинская средняя школа №1
Урок - консультация в 11 классе
по теме «Задачи на смеси и сплавы»
Подготовила: учитель математики
Белогурова Н.С.
с. Зеренда
2013-2014 учебный год
Урок - консультация в 11 классе по теме «Задачи на смеси и сплавы»
Цели: закрепить умение рассуждать и решать задачи на дроби и проценты, составлять по задаче уравнения и решать его, научить решать задачи на смеси и сплавы арифметическим способом.
I. Организационный момент.
Задачи, которые мы будем решать, относятся к традиционным задачам математики. Они охватывают большой круг ситуаций: смешение товаров разной цены, жидкостей с различным содержанием соли, кислот разной концентрации, сплавление металлов с различным содержанием некоторого металла. Когда-то они имели исключительно практическое значение. В настоящее время эти задачи часто встречаются в тестах на выпускных экзаменах и на вступительных экзаменах в вузы.
Мы рассмотрим задачи на смешение, которые можно решить не только алгебраически, то есть с помощью уравнения, но и арифметическим способом.
Для успешной работы нам понадобится повторить основные понятия этой темы.
II. Устный счёт
1. Концентрация вещества в смеси - это часть, которую составляет масса вещества в смеси от массы смеси. Нахождение части от целого. В химии вы называли эту величину массовой долей вещества.
Концентрация вещества может быть указана и числом и %.
2. Объясните значение высказываний:
а) Концентрация раствора 3 %;
(В 100 г раствора содержится 3 г вещества).
в) Молоко имеет 1,5 % жирности;
(В100 г молока содержится 1,5 г жира).
с) золотое кольцо имеет 583 пробу?
(В1 г кольца содержит 583 миллиграмма золота).
Сколько сахара содержится в 200 г 10%- го сахарного сиропа?
Теперь давайте попробуем решить устно несколько задач.
3. К одной части сахара прибавили 4 части воды. Какова концентрация полученного раствора?
(1: 5 ·100 = 20 %)
4. Килограмм соли растворили в 9 л воды. Какова концентрация раствора?
(1 : 10 ·100 = 10%)
III. Разбор задач
Следующие задачи мы решим с вами с помощью уравнения.
I Задачи на сушку грибов, ягод.
Важно помнить, что количество тв. вещ-ва в свежих и сухих грибах, ягодах и т.д. постоянное, изменяется количество воды.
№1. Свежие абрикосы содержат 80 % воды по массе, а курага (сухие абрикосы) - 12 % воды. Сколько понадобится килограммов свежих абрикосов, чтобы получить 10 кг кураги?
Решение: Составим таблицу:
Свежие абрикосы
Курага
Масса, кг
Х кг
10 кг
вода
80 %
12 %
Тв. вещ., %
20 %
88 %
Тв. вещ., кг
х∙0,2
10∙0,88
Количество тв. вещ-ва в свежих и сухих абрикосов постоянное, изменяется количество воды.
Составим уравнение: 0,2х=10∙0,88
Х=44
Ответ: 44 кг.
№ 2 Свежие грибы по весу содержат 90% воды, а сухие 12% воды. Сколько получится сухих грибов из 22 кг свежих?
2,2=0,88х
Ответ:2,5 кг.
№ 3. Свежесрезанные грибы содержат 90% воды. После длительного хранения 120 кг грибов на складе содержание воды в них уменьшилось до 84%. Какой стала масса грибов после хранения?
120∙0,1=0,16х
Х= 75
Ответ: 75 кг
II Задачи на смешение двух растворов, решаемые алгебраически.
№1. В каких пропорциях нужно смешать раствор 50 % и 70 % кислоты, чтобы получить раствор 65 % кислоты?
Для решения задачи я попрошу вас заполнить таблицу, которая находится у вас на столе.
Концентрация
Масса раствора ( г )
Масса кислоты ( г )
I раствор
50
х
0,5х
II раствор
70
у
0,7у
смесь
65
х+у
0,65(х+у)
Заполняем 1-й столбик. Здесь мы указываем концентрацию растворов.
Заполняем 2-й столбик. Здесь мы указываем массу каждого раствора. Предположим, что первого раствора нужно взять х г, а второго у г. Считаем, что при смешении нет потерь массы, то есть масса смеси равна сумме масс смешиваемых растворов.
Тогда масса смеси будет (х + у) г.
Теперь заполним 3-й столбик. Найдем количество чистой кислоты в 1-ом растворе. Это 0,5х г, во втором растворе 0,7у г, а в смеси будет 0,65(х + у) г кислоты.
По условию задачи составим и решим уравнение.
0,65 (х + у) = 0,5 х + 0,7 у,
65 х - 50 х = 70 у - 65 у,
15 х = 5 у,
3 х = 1 у,
х : у = 1 : 3.
Нужно взять: 1 часть раствора 50% кислоты и 3 части раствора 70% кислоты
Ответ: 50% раствора кислоты -1 часть, 70% раствора кислоты - 3 части.
А теперь я хочу предложить вам схему решения этой задачи арифметическим методом, который позволяет решить ее практически устно. Запишем концентрацию каждого раствора кислоты и концентрацию смеси так:
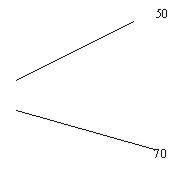
![]()
Вычислим, на сколько концентрация первого раствора кислоты меньше, чем концентрация смеси и на сколько концентрация второго раствора кислоты больше, чем концентрация смеси и запишем результат по линиям:
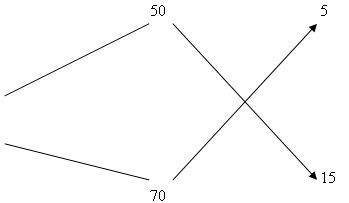
Таким образом, 5 частей нужно взять 50% раствора кислоты и 15 частей 70% раствора кислоты, то есть отношение взятых частей ![]() . Окончательно получаем: 50% раствора кислоты-1 часть, 70% раствора кислоты-3 части. Сравните полученные результаты. Делаем вывод: получили один и тот же ответ, но времени затратили гораздо меньше.
. Окончательно получаем: 50% раствора кислоты-1 часть, 70% раствора кислоты-3 части. Сравните полученные результаты. Делаем вывод: получили один и тот же ответ, но времени затратили гораздо меньше.
Этот метод решения назвали «правило креста». «Правилом креста» называют диагональную схему правила смешения для случаев с двумя растворами. Слева на концах отрезков записывают исходные массовые доли растворов (обычно слева вверху - большая), на пересечении отрезков - заданная, а справа на их концах записываются разности между исходными и заданной массовыми долями. Получаемые массовые части показывают, в каком отношении надо слить исходные растворы.
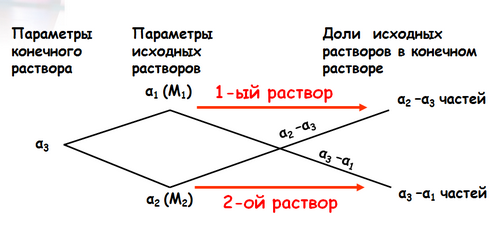
№2. В каких пропорциях нужно сплавить золото 375 пробы с золотом 750 пробы, чтобы получить золото 500 пробы?
И так составляем схему.
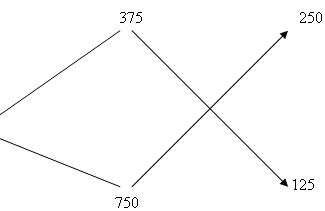
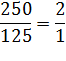 Чтобы получить золото 500 пробы нужно взять: 2 части золота 375 пробы и 1 часть золота750 пробы.
Чтобы получить золото 500 пробы нужно взять: 2 части золота 375 пробы и 1 часть золота750 пробы.
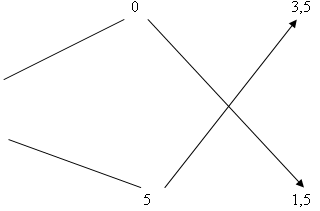
№3. Морская вода содержит 5 % соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5 %?
![]()
![]()
Откуда х=70 кг.
Или нужно взять 7 частей пресной воды и 3 части морской воды. По условию нам известно, что морской воды 30 кг и это 3 части нового раствора. Значит, на одну часть приходится 10 кг. Следовательно, 7частей пресной воды - это 70 кг.
Ответ: нужно добавить 70 кг пресной воды.
IV Задачи для самостоятельного решения
Следующие задачи решить удобным для вас способом.
№4. Имеется два сплава с разным содержанием меди. В первом сплаве содержится 40%, а во втором - 70% меди. В каком отношении надо взять первый и второй сплавы, чтобы из них получить новый сплав, содержащий 60% меди?
Решение: пусть X - масса сплава, 40% содержанием меди, Y - масса сплава с 60% содержанием меди. 0,4X - масса меди в первом сплаве, 0,7Y - масса меди во втором сплаве, 0,6(X +Y) - масса меди в новом сплаве. Составим уравнение: 0,4X+0,7Y=0,6(X +Y). Решив уравнение, имеем, что X: Y=1:2.
Ответ: необходимо взять одну часть 40% сплава и две части 70% сплава.
№5. В куске сплава меди и цинка количество меди увеличили на 40%, а количество цинка уменьшила на 40%. В результате общая масса куска сплава увеличилась на 20%. Определите процентное содержание меди и цинка в первоначальном куске сплава.
Решение: пусть X - масса меди в сплаве, Y - масса цинка в сплаве. Если количество меди увеличить на 40%, то масса меди составит 1,4 X, если уменьшить на 40% количество цинка, то масса цинка составит 0,6 Y. Масса всего куска увеличится на 20%, а значит будет составлять 1,2(X +Y). Составим уравнение: 1,4 X+0,6 Y=1,2(X +Y). Решив уравнение, имеем:
X: Y=3:1. Процентное содержание меди: 0,75=75%, цинка 0,25=25%.
Ответ: 75% меди и 25% цинка в сплаве.
№6. Смешали 30%-ный и 50%-ный раствор азотной кислоты и получили 45%-ный раствор. Найдите отношение массы 30% раствора к массе 50% раствора.
Решение: пусть X - масса 30% раствора азотной кислоты, Y - масса 50% раствора азотной кислоты. 0,3X - масса азота в первом растворе, 0,5Y - масса азота во втором растворе, 0,45(X +Y) - масса азота в новом растворе. Составим уравнение: 0,3X+0,5Y=0,45(X +Y). Решив уравнение, имеем, что X: Y=1:3.
Ответ: необходимо смешать одну часть 30% раствора и три части 50% раствора.
№7. Соединили два сплава с содержанием меди 40% и 60% и получили сплав, содержащий 45% меди. Найдите отношение массы сплава с 40% содержанием меди к массе сплава с 60% содержанием меди.
Решение: пусть X - масса сплава, 40% содержанием меди, Y - масса сплава с 60% содержанием меди. 0,4X - масса меди в первом сплаве, 0,6Y - масса меди во втором сплаве, 0,45(X +Y) - масса меди в новом сплаве. Составим уравнение: 0,4X+0,6Y=0,45(X +Y). Решив уравнение, имеем, что X: Y=3:1.
Ответ: необходимо взять три части 40% сплава и одну часть 60% сплава.
№8 Имеются два сплава, в одном из которых содержится 20%, в другом 30% олова. Сколько нужно взять первого и второго сплава, чтобы получить 10 кг нового сплава, содержащего 27% олова?
Ответ: 3 кг , 7 кг.
№9 Имеются два сплава, в одном из которых содержится 40%, а во втором 20% серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы получить сплав, содержащий 32% серебра?
![]()
№10 Имеются два сплава, в одном из которых содержится 10%, а в другом - 20% меди. Сколько нужно взять первого и второго сплавов, чтобы получить 15 кг нового сплава, содержащего 14% меди?
Ответ: 9 кг и 6 кг.
№ 11 Имеются два сплава, в одном из которых содержится 30%, а в другом - 50% золота. Сколько кг второго сплава нужно добавить к 10 кг первого, чтобы получить сплав, содержащий 42% золота?
Ответ: 15 кг.
№12 Из молока, жирность которого 5%, делают творог, жирностью 0,5%. Определить, сколько творога получается из 1 тонны молока?
Ответ: 300 кг.
№13 При смешивании растворов, содержащих 25% и 60% кислоты, получился раствор, содержащий 39% кислоты. Определить в какой пропорции были смешаны растворы?
Ответ: 3 : 2.
№ 14. Какое количество воды надо добавить к 100 граммам 70%-ной уксусной эссенции, чтобы получить 5% раствор уксуса?
Ответ: 1300 гр.
№15. Морская вода содержит 5% соли. Сколько килограммов пресной воды надо добавить к 40 кг морской воды, чтобы содержание соли в последней составляло 2%.
Ответ: 60 кг.
№16. Кусок сплава меди с оловом весом 2 кг содержит 45% меди. Сколько чистого олова надо прибавить к этому куску, чтобы получившийся новый сплав имел 40% меди?
Ответ: 1,5 кг.
№17 Сколько чистого спирта надо прибавить к 735 г 16%-ного раствора йода в спирте, чтобы получить 10%-ный раствор?
Ответ: 441 г.
№18 . Кусок сплава меди и цинка массой в 36 кг содержит 45% меди. Какую массу меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 60% меди?
36∙0,45+х=0,6∙36+х
Ответ: 13,5 кг.
V. Самостоятельная работа. (решить арифметическим способом задачи)
1. Сколько граммов 75% - ного раствора кислоты надо добавить к 30 г 15%-ного раствора кислоты, чтобы получить 50%- ный раствор кислоты?
2. При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?
VI.Домашнее задание. (разложены карточки на парты с домашнем заданием)
1.Сколько граммов воды надо добавить к 180 г сиропа, содержащего 25% сахара, чтобы получить сироп, концентрация которого равна 20%?
2. Имеется кусок сплава цинка с железом общей массой 24 кг, содержащий 20% цинка. Сколько килограммов чистого железа надо добавить к этому куску сплава, чтобы получившийся сплав содержал 15% цинка?
3. Составить задачу на смешение и решить ее алгебраическим способом. Какие это могут быть задачи? На смешение товаров разной цены, жидкостей с различным содержанием соли, кислот разной концентрации, сплавление металлов с различным содержанием некоторого металла. Запишите условие задачи, приведите схему решения и решите ее. Несколько лучших задач мы рассмотрим на доске.
Подведем итог урока.
8