Предмет: математика

Класс: 5

Тема: «Сравнение обыкновенных дробей»

Тип урока: ОНЗ

Учебник: Мерзляк А.Г., Полонский В.Б. Математика. 5 класс

Автор урока: Л.Б. Васильева учитель математики МБОУ «Ривзаводская СОШ»

Максатихинского района Тверской области.

Основные цели:

Метапредметные:

1) тренировать умение фиксировать шаги по построению нового знания, умение работать в парах, умение адекватно оценивать свою деятельность;

2) сформировать мотивацию к учебной деятельности как одно из средств развития и социализации личности учащихся.

Предметные:

1) сформировать умение строить алгоритмы на примере алгоритма сравнения обыкновенных дробей.

Материалы к занятию:

Демонстрационный материал: 1) задание на актуализацию знаний; 2) задание на устный счёт (тема урока); образец для проверки; 3) задание для пробного действия; 4) эталон.

Раздаточный материал: 1) ножницы, цветные шаблоны; 2) задание на первичное закрепление во внешней речи; 3) основа для выполнения самостоятельной работы; 4) рабочие тетради на печатной основе.

Ход урока

1. Мотивация к учебной деятельности.

− Доброе утро, ребята.

− Скажите, пожалуйста, что нового вы узнали на предыдущих уроках? (Мы узнали, что такое доли и обыкновенные дроби, как записать и как прочитать дробь, как изобразить дробь на координатном луче.)

− Сегодня вы продолжите знакомство с обыкновенными дробями, а значит, будете открывать новые знания, как вы будете это делать? (Мы выясним, что мы не знаем и сами найдем новые знания.)

2. Актуализация знаний и фиксирование индивидуального затруднения в пробном действии.

− Но для того, чтобы работа была успешной, начнем урок с повторения.

− Расположи ответы примеров в порядке возрастания.

Учащиеся самостоятельно выполняют задание.

− Сравните свои результаты с образцом:

4 12 30 36 40 54 68 108 2100

− Какими знаниями вы воспользовались, чтобы выполнить задание? (Устными способами умножения и деления натуральных чисел, правилом сравнения натуральных чисел.)

− Какое слово вы получили? (Сравнение.)

− Вы умете сравнивать натуральные числа? (Да, умеем.)

− Тогда сравнению, каких чисел будет посвящен урок? (Сравнению дробей.)

Тема фиксируется на доске.

− Что надо повторить, если вы так определили тему урока? (Что такое дроби, какие способы сравнения дробей мы знаем.)

На доске ряд дробей: .

− На какие группы можно разбить все дроби? (Дроби, у которых одинаковые числители, дроби, у которых одинаковые знаменатели.)

На доске:

− Назовите знаменатели дробей первой группы. (3, 5, 6.)

− Что показывает знаменатель дроби? (Знаменатель показывает, на сколько равных частей разделено целое.)

− Назовите числители дробей второй группы. (11, 4, 3.)

− Что показывает числитель дроби? (Числитель показывает, сколько равных частей целого взято.)

− Что можно использовать для сравнения дробей? (Модно использовать числовой луч.)

− Что в сейчас повторили? (Что такое дробь, что показывают знаменатель и числитель дроби, как можно сравнить дроби.)

− Какое следующее задание вы будете выполнять, чтобы узнать, что вы не знаете? (Пробное задание.)

− Посмотрите на две группы дробей и скажите, в каком порядке в той и другой группе расположены дроби. Ответ обоснуйте. Время выполнения 10 сек.

− У кого нет ответа?

− Что вы не можете сделать? (Я не могу определить, в какой последовательности расположены дроби.)

− У кого есть обоснованный ответ?

− Что вы не можете сделать? (Я не могу дать обоснованный ответ.)

− Что надо сделать, если возникло затруднение? (Надо остановиться и подумать, почему возникло затруднение.)

3. Выявление причины затруднения.

- Какое задание вы должны были выполнить? (Надо было определить для каждой группы дробей, в какой последовательности они стоят.)

- Почему возникли затруднения? (Не знаем способа сравнения дробей.)

4. Построение проекта выхода из затруднения.

− Сформулируйте цель вашей деятельности. (Узнать способ сравнения дробей.)

− Какие дроби входят в каждую группу? (В первую группу входят дроби с одинаковыми числителями, а во вторую с одинаковыми знаменателями.)

− По какому признаку будем сравнивать дроби? (По одинаковым числителям или одинаковым знаменателям.)

− Уточните цель вашей деятельности. (Построить правило сравнения дробей с одинаковыми числителями и правило сравнения дробей с одинаковыми знаменателями.)

− Открывать знания вы будете в группах. Какие правила надо выполнять, чтобы работа в группах была успешной? (В группе должен быть организатор, все должны работать на конечный результат, если что-то не понял, переспроси, несогласие высказывай вежливо, один говорит, остальные слушают.)

− Первая, третья и пятая группы будут работать с первой группой дробей, а вторая, четвертая и шестая - со второй группой дробей.

− Сколько кругов должно быть у каждой группы (По три круга.)

− На сколько равных частей должны быть разбиты круги у 1, 3, 5 групп? (На 3, 5 и 6 равных частей.)

− На сколько равных частей должны быть разбиты круги у 2, 4, 6 групп? (На 12 равных частей.)

− По какому плану вы будете работать? (Разделим круги на необходимое количество равных частей, возьмем то количество частей, которое соответствует числителям дробей, сравним, взятые части, сделаем вывод, сформулируем правило.)

− Какое правило будут формулировать 1, 3 и 5 группы. (Правило сравнения дробей с одинаковыми числителями.)

− Какое правило будут формулировать 2, 4 и 6 группы. (Правило сравнения дробей с одинаковыми знаменателями.)

5. Реализация проекта выхода из затруднения.

На столах у групп 1, 3, 5 лежит по три круга один разделен (пунктирными линиями) на 3 равные части, второй - на 5, третий - на 6.) У групп 2, 4, и 6 - по три круга, которые разделены на 12 равных частей.

Учащиеся работают по реализации плана самостоятельно.

Одна из нечетных групп и одна их четных групп озвучивают ход своей работы и полученные выводы.

Вывод 1:

Из двух дробей с одинаковыми числителями та дробь больше (меньше), знаменатель, которой меньше (больше).

Вывод 2:

Из двух дробей с одинаковыми знаменателями та дробь больше (меньше), числитель, которой больше (меньше).

На доске фиксируется общий алгоритм сравнения дробей:

АЛГОРИТМ СРАВНЕНИЯ ДРОБЕЙ

Рассмотреть дроби

Да

Нет

Больше (меньше) та дробь, у которой больше (меньше) числитель

Больше (меньше) та дробь, у которой меньше (больше) знаменатель

− Теперь вы сможете ответить на вопрос пробного действия: в каком порядке в группах расположены дроби? (В порядке убывания.)

− Обоснуйте свой ответ. (В первой группе дроби с одинаковыми числителями, а знаменатели расположены в порядке возрастания, значит, сами дроби расположены в порядке убывания. Во второй группе дроби с одинаковыми знаменателями, а числители расположены в порядке убывания, значит, и сами дроби расположены в порядке убывания.)

6. Первичное закрепление во внешней речи.

− Что теперь необходимо сделать? ( Надо научиться использовать алгоритм сравнения дробей.)

Работа в парах.

− Сравнить дроби, проговаривая алгоритм сравнения:

и ; и ;

и ; и .

После выполнения работы учащиеся проверяют по образцу:

> ; < ;

< ; > .

− У каких пар возникли затруднения?

− При сравнении, каких дробей?

− Какой шаг алгоритма нарушили?

− У каких пар не возникло затруднений?

7. Самостоятельная работа с самопроверкой по эталону.

− А теперь проверьте, как каждый из вас понял, применения алгоритма сравнения дробей.

Сравнить дроби:

и ; и ;

и ; и .

После выполнения задания, учащиеся сопоставляют свои работы с эталоном для самопроверки

- У кого задание вызвало затруднение?

- В чём причина возникшего затруднения?

- У кого задание выполнено правильно?

8.Включение в систему знаний.

− Расположите дроби в порядке возрастания:

Я Е И У А Ч Щ С

− Какое слово получили? (УЧАЩИЕСЯ.)

− Расположите дроби в порядке убывания:

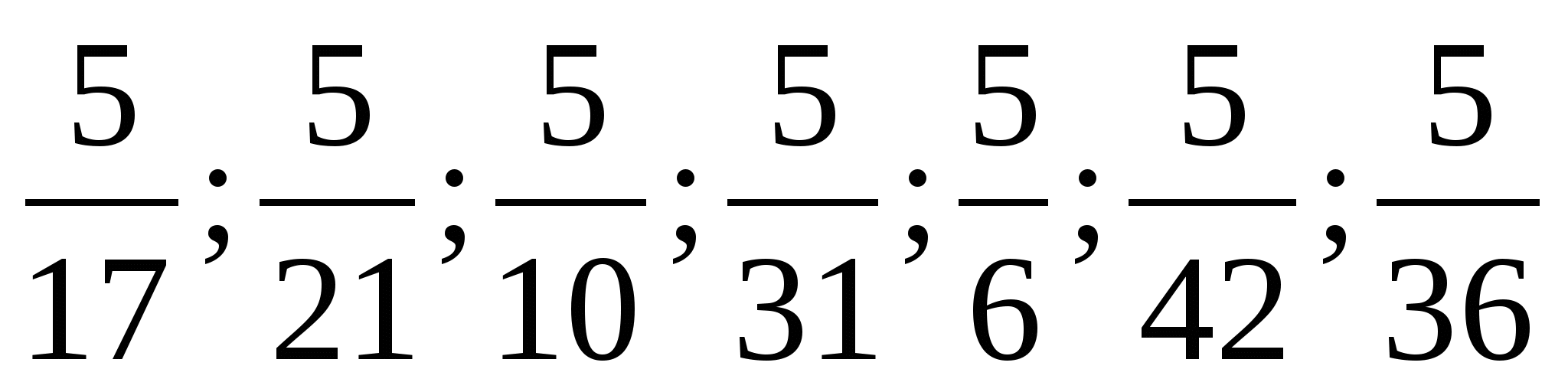
Л О О Д М Ы Ц

− Какое слово получили? (МОЛОДЦЫ.)

− К каким учащимся можно отнести это определение? (Учащимся нашего класса.)

− Почему? (Ответы детей.)

Дальше можно продолжить работу в рабочих тетрадях с печатной основой (автор Т.М. Ерина). Задания с цветными карандашами.

9.Рефлексия деятельности на уроке.

− Что нового вы сегодня узнали? (Мы узнали правила сравнения обыкновенных дробей с одинаковыми числителями или с одинаковыми знаменателями.)

− Что вы создали? (Мы создали алгоритм сравнения обыкновенных дробей.)

− Как вы это делали? (Ответы детей.)

− Оцените свою деятельность на уроке: большой палец вверх, если вы поняли, как сравнивать дроби и в самостоятельной работе не допустили ошибок, или вниз, если вы поняли, как сравнивать дроби, но в самостоятельной работе ошибки были.

Домашнее задание: &. 26, задание на сравнение обыкновенных дробей;

творческое задание:

1) Изобразить портрет трёх дробей с одинаковыми знаменателями.

</ 2) Изобразить портрет трёх дробей с одинаковыми числителями.

~ 6 ~