Содержание

1. Введение 2

2. Основная часть 4

2.1. Виды бантиков 4

2.1.1. Простой бантик 4

2.1.2. Сложный бантик 4

2.1.2. Трехъярусный бантик 5

2.2. Виды коробок 5

2.2.1. Куб 5

2.2.2. Прямоугольный параллелепипед 5

2.2.3. Цилиндр 5

2.2.4. Конус 6

2.3. Формула длины ленты, связывающая форму коробки и бантика 6

3. Заключение 7

4. Список литературы 8

5. Приложения 9

1. Введение

Актуальность исследования. Я не в первый раз участвую в различных дистанционных олимпиадах, но во Всероссийской дистанционной эвристической олимпиаде «Эйдос» по математике участвовала в первый раз. Мне очень понравилась эта олимпиада, потому что математика - мой любимый предмет. Именно эта математическая олимпиада не похожа на другие, в которых я принимала участие. Известно, что математика - точная наука. Но при выполнении заданий этой олимпиады, понимаешь, что исследования открывают путь в необычный мир, полный загадок, и как приятно сделать эти открытия самой! Чувствуешь себя не просто ученицей, а учёным - исследователем. Я поняла, что не всё можно решить с помощью формул и правил, а необходимо пользоваться своей фантазией, рассуждением и подбором. Самым трудным для меня было правильно сформулировать мысль, чтобы её поняли, и она прозвучала красиво, а также выбрать наиболее точные и максимально интересные ответы, так как в ходе работы у меня появилось несколько решений. В каждом задании я открывала для себя какую-нибудь интересную особенность, углубляла и дополняла свои знания. Эта олимпиада - ключ от дверей в мир идей. Она доставляет эстетическое удовольствие. В своей работе я покажу решение одного из заданий, а именно «Формулу бантика», за которое мне присуждено звание Лауреата ХХII - ой Всероссийской дистанционной эвристической олимпиады «Эйдос» по математике. На первый взгляд, вроде бы такая мелочь, как длина подарочной ленты и что может быть проще? А оказывается это можно развить в интереснейшую тему. Решение этой задачи дает возможность не просто вести сухие математические вычисления, оно развивает художественные навыки и логическое мышление. Это задание творческого характера. Я получила удовольствие от его выполнения. Сразу представила новогодний праздник, кучу подарков, так как олимпиада проходила в преддверии Нового года, при этом испытывала такое радостное возбуждение, что сразу забыла про усталость, которая накопилась при выполнении предыдущих заданий. Это задание меня очень заинтересовало, и после завершения олимпиады я продолжила свое исследование. Для этого я самостоятельно изучила неизвестные мне ранее формулы геометрии, а также формулу для вычисления погрешности.

Цель исследования - разработать проект оформления подарочной коробки и рассчитать длину ленты для её украшения.

Гипотеза. Существует формула, связывающая длину подарочной ленты от формы бантика и коробки.

Объект исследования - праздничная упаковка.

Предмет исследования - праздничные коробки и банты различной формы.

Проблема исследования заключается в выявлении связи длины подарочной ленты от формы коробки и бантика.

Задачи исследования - в соответствии с целью и проблемой исследования я поставила следующие задачи:

1. Найти какие по форме и строению банты могут украсить праздничную коробку;

2. Указать способы опоясывания коробки лентой;

3. Определить, как будет зависеть длина ленты для бантика, в зависимости от его формы;

4. Определить, как будет зависеть длина подарочной ленты от размеров коробки с подарком;

5. Вывести формулу, которая в дальнейшем позволила бы легко определить нужную длину ленты для упаковок подарков различной формы.

Методы исследования: сбор, изучение, анализ и обобщение экспериментального материала

2. Основная часть

Красивая новогодняя упаковка - это украшение любого подарка, возможность придать ему определенную загадочность, продлить время предвкушения чуда до того момента, когда сам подарок окажется в руках адресата, а декоративные ленты, бантики придают подарку более нарядный вид. [Приложение № 1]

Сегодня я постараюсь выбрать оформление подарочной коробки и рассчитать длину ленты , которая будет ее украшать.

2.1. Виды бантиков

Бант - главное украшение подарочной упаковки. Объемный и сверкающий, геометрической формы или устремленный в разные стороны, однотонный или пестрый, словно павлиний хвост, он придает подарку неповторимый облик.

2.1.1. Простой бантик

Простой бантик имеет 2 кольца-окружности (), узелок () и 2 хвостика (). Известно, что длина окружности равна . Примем, что , а , получим (). Пусть R=3 см, тогда необходимая длина ленты для такого банта равна 66 см. (). Такой бант можно сделать с четырьмя, шестью кольцами и т.д. Тогда формула банта будет выглядеть так:

• 2 кольца - L=22R;

• 4 кольца - L=С+22R;

• 6 колец, где - L= 2C+22R

2.1.2. Сложный бантик

Ленточку сворачиваем в несколько колец. Кольца должны быть равны диаметру бантика. Разглаживаем кольца, по краям делаем надрезы в виде треугольника. Полученные треугольники располагаем посередине, скрепляем ленточки стиплером и поочередно расправляем кольца с каждой стороны банта в разные стороны. В распушенный бантик посередине аккуратно проденем ленточку, опояшем коробку и под бантом прикрепим её стиплером, поправим кольца бантика так, чтобы не видно было места скрепления. Бантик: L = 2dn, где d - диаметр банта, n- количество колец, например: диаметр кольца равен 4 см и необходимо 6 таких колец, тогда L = 246=48 см, т.е. на такой бант необходимо будет 48 см. ленты.

2.1.2. Трехъярусный бантик

Д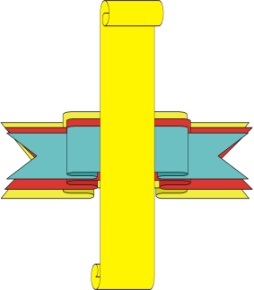ля создания такого банта нужно взять 3 разных по ширине () и цвету отрезка ленты, но равных по длине. Длина каждого отрезка должна быть равна величине банта (d). Сложить друг на друга, края отрезков отрезать в виде треугольника, посередине бантик скрепим стиплером (в дальнейшем, когда будет необходимо прикрепить бантик к коробке необходимо сверху скрепления частей (посередине) провести еще одной лентой, которой в дальнейшем перевяжем подарочную коробку.) В данном случае бантик будет состоять из 3 отрезков ленты разной ширины, но одинаковой длины. L= 3С, где С - длина банта. Представим, что мы хотим сделать такой бантик длиной 8 см., тогда нам будет необходимо взять 3 отрезка ленты по 8 см. разной ширины и разных цветов, всего 24 сантиметра.

Существуют ещё и другие виды бантиков. [Приложение № 2]

2.2. Виды коробок

Коробки бывают разных форм, в виде куба, прямоугольного параллелепипеда, цилиндра, конуса, и т.д. Рассмотрим некоторые из них.

2.2.1. Куб

Коробка имеет форму куба, значит, у нее все стороны равны . Длина ленты для коробки будет равна: , где - сторона коробки. Бантик можно взять любой и добавить формулу банта к формуле коробки. Например: бантик в данном случае взяли классический из 2 колец. L₁ - длина ленты для коробки, L₂ - длина ленты для банта. L = L₁ + L ₂ =22R + 4, если R = 3 см, =13 см, тогда для украшения коробки потребуется 108 см. ленты.

2.2.2. Прямоугольный параллелепипед

Чтобы украсить коробку такого вида примем высоту коробки за с, стороны основания - а. Пусть, , тогда , затем прибавим формулу того бантика, который хотим применить, например сложный, тогда .

2.2.3. Цилиндр

L = 2d +2h, пусть d = 1/2 h, где d -диаметр основания коробки, h - высота коробки, пусть d =1/2 h, тогда L = 3h. Коробку в форме цилиндра украсим простым бантом.

2.2.4. Конус

Коробку в виде конуса перевязать бантом не возможно, т.к. он будет съезжать, но нам очень хочется украсить ее бантом. Для этого необходимо сделать отдельно, какой захотите бантик, и прикрепить к коробке при помощи стиплера, скотча или клея ПВА, в зависимости от того из какого материала она сделана.

2.3. Формула длины ленты,

связывающая форму коробки и бантика

На Новый год сбылась моя мечта, мне родители подарили новые колонки для компьютера. Довольная своим подарком я решили украсить коробку из-под колонок, которая имеет форму прямоугольного параллелепипеда, сложным бантиком из яркой атласной ленты. [Приложение №3] Вспомнив свою работу, я вывела формулу длины ленты и сравнила ее с реально использованной лентой.

Для вычисления длины подарочной ленты я воспользуюсь формулой .

Размеры коробки , и , где , , , тогда , .

Для украшения моей коробки я сделала сложный бантик (п.2.1.2) с семью кольцами. , тогда , L=170+196=366 см.

Сравним полученный результат с фактической длиной ленты, использованной мною.

Формула, по которой я считала погрешность , где - приближенное значение, т.е. полученное по формуле, - точное значение. Из полученного результата вижу, что мою формулу для расчета длины ленты можно использовать на практике.

3. Заключение

Практическая значимость работы, на мой взгляд, заключается в следующем:

1. Рассмотрены различные формы подарочных упаковок и бантиков.

2. Выведена формула длины ленты для подарков различной формы.

3. Проведён социологический опрос команды МОУ «Средняя общеобразовательная школа № 8 с углублённым изучением отдельных предметов» г. Когалыма, участников ХХII-ой Всероссийской дистанционной эвристической олимпиады «Эйдос» по математике (6-7 класс, всего 17 человек), которая заняла 2 - е место из 12 команд-участников. [Приложение №4]

Результаты социологического опросаИсходя из результатов социологического опроса, видим, что задача №5 «Формула бантика» наиболее предпочтительна и является одной из самых творческих задач.

Результаты измерений рефлексии 5 задания «Формула бантика»

среди участников олимпиады 6- 7 классы МОУ «Средняя школа №8»

(средний бал по десятибалльной шкале)

1. В данной работе я рассмотрела только некоторые частные случаи форм коробок, бантов и способов упаковки.

2. Я вывела формулу упаковки подарка. Эту идею с формой коробки и бантика можно развивать бесконечно. Если мне не удастся стать юристом, то я могу работать в магазине и красиво упаковывать подарки. Спасибо «Эйдосу» за помощь в выборе моей будущей профессии. Желаю, чтобы все олимпиады были такими же интересными и не ординарными.

Удачи мне, всем моим друзьям и соперникам!

4. Список литературы

1. М. Д. Аксенова. Энциклопедия для детей. Математика. Т. 11. Издательский центр «Аванта +», 2001.

2. В.А. Гусев, А.Г. Мордкович. Математика: Алгебра: Геометрия: Приложения: Справочные материалы: Учебное пособие для учащихся-М.: Просвещение.1986.

3. Геометрия в таблицах. 7-11кл.: справочное пособие/автор составитель Л.И. Звавич, А.Р. Рязановский.-12-е изд., стереотип.-М.: Дрофа, 2007.

4. SuperCook.ru

</ 5. Приложения