- Учителю
- Методические рекомендации по подготовке к дифференцированному зачету по дисциплине ЕН. 03 Теория вероятностей и математическая статистика по специальности СПО 230115 Програм
Методические рекомендации по подготовке к дифференцированному зачету по дисциплине ЕН. 03 Теория вероятностей и математическая статистика по специальности СПО 230115 Програм
Департамент образования Ямало-Ненецкого автономного округа
Государственное бюджетное образовательное учреждение
среднего профессионального образования
«Ноябрьский колледж профессиональных и информационных технологий»
Ямало-Ненецкого автономного округа
Методические рекомендации для обучающихся
по подготовке к дифференцированному зачету
по дисциплине
ЕН.03 Теория вероятностей и математическая статистика
по специальности СПО
230115 Программирование в компьютерных системах
(углубленной подготовки)
2013 г.
Методические рекомендации составлены с целью оказания помощи обучающимся при подготовке к дифференцированному зачету по дисциплине ЕН.03 Теория вероятностей и математическая статистика по специальности среднего профессионального образования 230115 Программирование в компьютерных системах (углубленной подготовки).
Рекомендации содержат общие положения о дифференцированном зачете; требования к сформированности общих и профессиональных компетенций, предъявляемых ФГОС; типовые задания для оценки освоения учебной дисциплины, указаны основные правила и требования к организации экзамена; расписаны критерии оценки, определяющие уровень сформированности знаний и умений.
Организация-разработчик: ГБОУ СПО «Ноябрьский колледж профессиональных и информационных технологий» ЯНАО
Разработчик: Каргина Н.Ю. - к.п.н., преподаватель высшей квалификационной категории ГБОУ СПО «Ноябрьский колледж профессиональных и информационных технологий» ЯНАО
Разделы содержания
С.
Введение
1. Общие методические указания по организации деятельности обучающихся в период подготовки к дифференцированному зачету
2. Результаты освоения дисциплины подлежащие оцениванию на дифференцированном зачете
3. Типовые задания для оценки освоения дисциплины
4. Условия организации и проведения дифференцированного зачета
5. Список рекомендуемой литературы
6. Список использованной литературы
Введение
Методические рекомендации для обучающихся по подготовке к дифференцированному зачету разработаны на основе Федерального государственного образовательного стандарта, рабочей программы дисциплины ЕН.03 Теория вероятностей и математическая статистика по специальности СПО 230115 Программирование в компьютерных системах (углубленной подготовки).
Итоговый контроль направлен на проверку конкретных результатов обучения, выявление степени овладения обучающимися системой знаний, умений и навыков, полученных в процессе изучения дисциплины ЕН.03 Теория вероятностей и математическая статистика.
Итоговый контроль - это контроль интегрирующий, он позволяет судить об общих достижениях обучающихся. При подготовке к нему происходит более углубленное обобщение и систематизация усвоенного материала, что позволяет знания и умения поднять на новый уровень. А это, в свою очередь, будет способствовать формированию общих и профессиональных компетенций. При систематизации и обобщении знаний и умений обучающихся проявляется в большей степени и развивающий эффект обучения, поскольку на этом этапе особенно интенсивно формируются и систематизируются интеллектуальные умения и навыки.
Итоговый контроль по дисциплине ЕН.03 Теория вероятностей и математическая статистика предусмотрен в виде зачетной контрольной работы.
Дифференцированный зачет проводится с целью контроля и оценки результатов освоения учебной дисциплины ЕН.03 Теория вероятностей и математическая статистика по специальности СПО 230115 Программирование в компьютерных системах (углубленной подготовки) в соответствии с требованиями ФГОС.
-
Общие методические указания
по организации деятельности обучающихся
в период подготовки к дифференцированному зачету
Дифференцированный зачет осуществляется после успешного прохождения обучающимися полного комплекса текущего и промежуточного контроля. Дифференцированный зачет проводится в виде выполнения контрольной работы.
Успешность сдачи зачетной контрольной работы зависит от нескольких факторов. Основной из них - активность, системность и целенаправленность учебной деятельности в течение семестра. Это относится ко всем без исключения обучающимся. Следующий по важности фактор - выбор правильной методики подготовки.
Рекомендации для подготовки к зачетной контрольной работе:
-
Обеспечьте дома удобное место для занятий.
-
Распределите материал для подготовки по количеству времени, оставшемуся до сдачи экзамена.
-
Определите для себя наиболее сложные вопросы и выделите время для возврата к ним в ходе подготовки.
-
Соблюдайте технику безопасности за персональным компьютером.
-
Приучайте себя контролировать режим подготовки, не допускайте перегрузок.
-
Делайте короткие перерывы, проводите гимнастику для глаз.
2. Результаты освоения дисциплины подлежащие оцениванию на дифференцированном зачете
2.1. Учебная дисциплина способствует формированию следующих знаний и умений
Таблица 2.1.
Результаты обучения (освоенные умения,
усвоенные знания)
Формы и методы контроля и
оценки результатов обучения
умения:
- применять стандартные методы и модели к решения вероятностных и статистических задач;
Практическая работа
Оценка выполнения самостоятельной работы
Наблюдение, анализ и оценка оптимальности метода решения вероятностных и статистических задач
Тестирование
Исследовательская работа
- пользоваться расчетными формулами и таблицами, графиками при решении статистических задач;
Практическая работа
Наблюдение и оценка во время проведения практических занятий
Оценка выполнения самостоятельной работы
Исследовательская работа
- пользоваться расчетными формулами и таблицами, графиками при решении статистических задач.
Практическая работа
Наблюдение, анализ и оценка умений применения пакета прикладных статистических программ
Оценка выполнения самостоятельной работы
Исследовательская работа
знания:
- основные понятия комбинаторики;
Тестирование
Анализ и оценка выполнения индивидуальных заданий
Дифференцированный зачет
- основы теории вероятностей и математической статистики;
Тестирование
Анализ и оценка выполнения индивидуальных заданий, исследовательских проектов
Дифференцированный зачет
- основные понятия теории графов.
Тестирование
Анализ и оценка выполнения индивидуальных заданий, исследовательских проектов
Дифференцированный зачет
-
Типовые задания для оценки освоения дисциплины
3.1. Выполнение тестовых заданий
3.1.1 Инструкция для обучающегося
Выполните задания. Решение должно быть полным, записывайте ход решения задачи и все необходимые математические выкладки. Полученный ответ следует округлять до двух значащих цифр. Во время выполнения заданий можно использовать калькулятор, ПК без выхода в Интернет.
Время выполнения зачетной работы - два часа (120 минут).
Алгоритм решения типовой задачи на непосредственный подсчет вероятности случайного события сводится к следующему:
-
Определение общего числа возможных исходов
 ;
; -
Анализ и расчет количества исходов, благоприятствующих случайному событию, т.е. таких, в которых данное событие обязательно произойдет;
3. Определение искомой вероятности события по формуле.
-
Варианты заданий
Вариант 1
1. Каждый из девяти человек обменялся рукопожатиями с восемью остальными. Сколько было рукопожатий?
2. В шахматном кружке 12 юношей и 8 девушек. Для участия в соревнованиях из них нужно составить команду, в которую должны войти 9 юношей и 3 девушки. Сколькими способами это можно сделать?
3. Из урны, содержащей первоначально 20 белых и 10 черных шаров, пропал один какой-то шар. После этого из неё наугад извлекают шар. Какова вероятность того, что это будет белый шар?
4. Из общего числа 1000 лотерейных билетов 100 билетов - выигрышные. Какова вероятность того, что из 5 купленных билетов хотя бы один окажется выигрышным?
5. Из урны, содержащей 6 белых, 4 черных и 2 оранжевых шара, наугад одновременно извлекают 3 шара. Какова вероятность того, что это будет шары одного цвета?
6. При каждом выстреле, независимо от остальных выстрелов, стрелок попадает в мишень с вероятностью 0,8. Ему разрешено стрелять до первого попадания. Какова вероятность того, что стрелок произведет ровно три выстрела?
7. Круговая мишень состоит из трёх зон. Вероятность попадания в эти зоны при одном выстреле соответственно равны 0,1; 0,35; 0,4. Найти вероятность попадания в первую или третью зоны.
8. Вероятность попадания в цель при одном выстреле равна 0,7. Выстрелы производят по одному до первого попадания. Определить вероятность того, что придется производить четвёртый выстрел.
9. Три студента сдают экзамен. Вероятность того, что отдельный студент сдаст экзамен на «отлично», равна для первого студента - 0,7, для второго - 0,6, для третьего - 0,2. Какова вероятность того, что экзамен будет сдан на «отлично» только одним студентом?
10. По заданной матрице построить сетевой график ( аijэлемент матрицы есть длительность работы от i до j в днях). Найти длину критического пути, указать экономию времени.
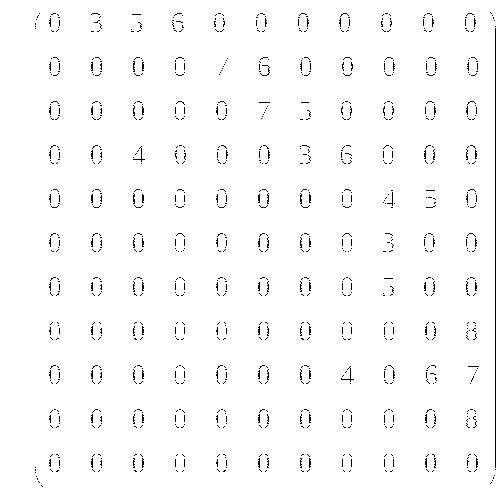
Вариант 2
1. Каждый из десяти человек обменялся рукопожатиями с девятью остальными. Сколько было рукопожатий?
2. В шахматном кружке 10 юношей и 6 девушек. Для участия в соревнованиях из них нужно составить команду, в которую должны войти 9 юношей и 3 девушки. Сколькими способами это можно сделать?
3. Из урны, содержащей первоначально 30 белых и 10 черных шаров, пропал один какой-то шар. После этого из неё наугад извлекают шар. Какова вероятность того, что это будет белый шар?
4. Из общего числа 1000 лотерейных билетов 10 билетов - выигрышные. Какова вероятность того, что из 5 купленных билетов хотя бы один окажется выигрышным?
5. Из урны, содержащей 6 белых, 7 черных и 1 оранжевых шара, наугад одновременно извлекают 3 шара. Какова вероятность того, что это будет шары одного цвета?
6. При каждом выстреле, независимо от остальных выстрелов, стрелок попадает в мишень с вероятностью 0,8. Ему разрешено стрелять до первого попадания. Какова вероятность того, что стрелок произведет ровно 2 выстрела?
7. Круговая мишень состоит из трёх зон. Вероятность попадания в эти зоны при одном выстреле соответственно равны 0,1; 0,35; 0,4. Найти вероятность попадания в первую или вторую зоны.
8. Вероятность попадания в цель при одном выстреле равна 0,7. Выстрелы производят по одному до первого попадания. Определить вероятность того, что придется производить третий выстрел.
9. Три студента сдают экзамен. Вероятность того, что отдельный студент сдаст экзамен на «отлично», равна для первого студента - 0,7, для второго - 0,6, для третьего - 0,2. Какова вероятность того, что экзамен будет сдан на «отлично» двумя студентами?
10. По заданной матрице построить сетевой график ( аijэлемент матрицы есть длительность работы от i до j в днях). Найти длину критического пути, указать экономию времени.
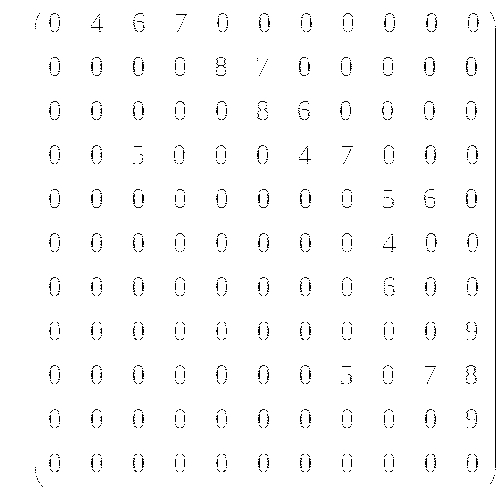
Вариант 3
1. Каждый из 11 человек обменялся рукопожатиями с 10 остальными. Сколько было рукопожатий?
2. В шахматном кружке 12 юношей и 6 девушек. Для участия в соревнованиях из них нужно составить команду, в которую должны войти 7 юношей и 2 девушки. Сколькими способами это можно сделать?
3. Из урны, содержащей первоначально 20 белых и 30 черных шаров, пропал один какой-то шар. После этого из неё наугад извлекают шар. Какова вероятность того, что это будет белый шар?
4. Из общего числа 1000 лотерейных билетов 50 билетов - выигрышные. Какова вероятность того, что из 5 купленных билетов хотя бы один окажется выигрышным?
5. Из урны, содержащей 4 белых, 9 черных и 2 оранжевых шара, наугад одновременно извлекают 3 шара. Какова вероятность того, что это будет шары одного цвета?
6. При каждом выстреле, независимо от остальных выстрелов, стрелок попадает в мишень с вероятностью 0,8. Ему разрешено стрелять до первого попадания. Какова вероятность того, что стрелок произведет ровно 5 выстрелов?
7. Круговая мишень состоит из трёх зон. Вероятность попадания в эти зоны при одном выстреле соответственно равны 0,1; 0,35; 0,4. Найти вероятность попадания во вторую или третью зоны.
8. Вероятность попадания в цель при одном выстреле равна 0,7. Выстрелы производят по одному до первого попадания. Определить вероятность того, что придется производить пятый выстрел.
9.Три студента сдают экзамен. Вероятность того, что отдельный студент сдаст экзамен на «отлично», равна для первого студента - 0,7, для второго - 0,6, для третьего - 0,2. Какова вероятность того, что экзамен будет сдан на «отлично» хотя бы одним студентом?
10. По заданной матрице построить сетевой график ( аijэлемент матрицы есть длительность работы от i до j в днях). Найти длину критического пути, указать экономию времени.

Вариант 4
1. Каждый из 12 человек обменялся рукопожатиями с 11 остальными. Сколько было рукопожатий?
2. В шахматном кружке 17 юношей и 4 девушек. Для участия в соревнованиях из них нужно составить команду, в которую должны войти 9 юношей и 3 девушки. Сколькими способами это можно сделать?
3. Из урны, содержащей первоначально 10 белых и 23 черных шаров, пропал один какой-то шар. После этого из неё наугад извлекают шар. Какова вероятность того, что это будет белый шар?
4. Из общего числа 1000 лотерейных билетов 25 билетов - выигрышные. Какова вероятность того, что из 5 купленных билетов хотя бы один окажется выигрышным?
5. Из урны, содержащей 3 белых, 9 черных и 2 оранжевых шара, наугад одновременно извлекают 3 шара. Какова вероятность того, что это будет шары одного цвета?
6. При каждом выстреле, независимо от остальных выстрелов, стрелок попадает в мишень с вероятностью 0,8. Ему разрешено стрелять до первого попадания. Какова вероятность того, что стрелок произведет ровно 4 выстрела?
7.Круговая мишень состоит из трёх зон. Вероятность попадания в эти зоны при одном выстреле соответственно равны 0,2; 0,35; 0,4. Найти вероятность попадания в первую или третью зоны.
8. Вероятность попадания в цель при одном выстреле равна 0,8. выстрелы производят по одному до первого попадания. Определить вероятность того, что придется производить пятый выстрел.
9. Три студента сдают экзамен. Вероятность того, что отдельный студент сдаст экзамен на «отлично», равна для первого студента - 0,7, для второго - 0,6, для третьего - 0,2. Какова вероятность того, что экзамен будет сдан на «отлично» ни одним студентом?
10. По заданной матрице построить сетевой график ( аijэлемент матрицы есть длительность работы от i до j в днях). Найти длину критического пути, указать экономию времени.

3.1.3 Критерии оценивания:
Время выполнения задания - 2 часа
Максимальное количество за правильное выполнение заданий - 100 баллов.
К![]()
У =
количество баллов, набранных обучающимися
максимальное количество баллов в заданиях
Если
КУ от 0,81 до 1,0
81 - 100 баллов
- «отлично»
КУ от 0,71 до 0,8
71 - 80 баллов
- «хорошо»
КУ от 0,61 до 0,7
60 - 70 баллов
- «удовлетворительно»
КУ менее 0,6
менее 60 баллов
- «неудовлетворительно»
4. Условия организации и проведения дифференцированного зачета
4.1. Условия проведения дифференцированного зачета
Дифференцированный зачет проводится в виде выполнения контрольной работы. Дифференцированный зачет проводится одновременно для всей учебной группы. Количество вариантов задания для сдающего зачет - каждому 1/4.
Время выполнения задания - 2 часа.
4.2. Оборудование: бумага, ручки, персональный компьютер.
5. Список рекомендуемой литературы:
Основная:
1. Горелов, Г.В., Кацко, И. А. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel: учебник для ССзуов. - Ростов н/Д: Феникс, 2009.
2. Омельченко, В.П., Курбатова, Э.В. Математика: учебное пособие. - Ростов н/Д.: Феникс, 2012.
3. Пехлецкий, И.Д. Математика - М.: Академия, 2010.
Дополнительная:
1. Акимов, О.Е. Дискретная математика: логика, группы, графы. - М.: Лаборатория базовых знаний, 2009.
2. Гарнаев, А.Ю. Самоучитель VBA. - СПб.: БХВ-Петербург, 2010.
3. Гмурман, В.Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 2010.
4. Калинина, В.Н., Панкин, В.Ф. Математическая статистика. - М.: Высшая школа, 2009.
Сайты в сети Интернет:
-
Онлайн библиотека [Электронный ресурс] - Режим доступа: .
-
Компьютерные электронные книги [Электронный ресурс] - Режим доступа: .
6. Список литературы
Нормативная литература:
-
ФГОС среднего профессионального образования по специальности 230115 Программирование в компьютерных системах (Утверждён приказом Министерства образования и науки РФ 23.06.2010 г. № 696).
-
Рабочая программа учебной дисциплины ЕН.03 Теория вероятностей и математическая статистика (углубленной подготовки).
Основная литература:
1. Горелов, Г.В., Кацко, И. А. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel: учебник для ССзуов. - Ростов н/Д: Феникс, 2009.
2. Ерусалимский, Я.М. Дискретная математика: теория, задачи, приложения. - М: Вузовская книга, 2009.
3. Кочетков, Е.С., Смерчинская, С.О., Соколов В.В. Теория вероятностей и математическая статистика: учебник. - М.: ФОРУМ: ИНФРА-М, 2010.
4. Омельченко, В.П., Курбатова, Э.В. Математика: учебное пособие. - Ростов н/Д.: Феникс, 2012.
5. Пехлецкий, И.Д. Математика - М.: Академия, 2010.
Сайты в сети Интернет:
-
Онлайн библиотека [Электронный ресурс] - Режим доступа: http://www.vbbooks.ru.
-
Интернет университет информационных технологий [Электронный ресурс] - Режим доступа: http: //www.intuit.ru.
-
Компьютерные электронные книги [Электронный ресурс] - Режим доступа: http://www.compebook.ru.