- Учителю
- Конспект урока на тему Арифметическая прогрессия (9 класс)
Конспект урока на тему Арифметическая прогрессия (9 класс)
11


Урок «Арифметическая прогрессия»
Цели урока: 1) образовательная: повторение материала по данным темам, формулы п-го члена и применение ее для нахождения первого члена, разности прогрессии и др.;
2) воспитательная: воспитание чувства коллективизма, личной ответственности перед товарищами по команде;
3) развивающая: развитие памяти, любознательности, активности.
Задачи учителя на уроке:
![]() проконтролировать знания основных формул арифметической прогрессии;
проконтролировать знания основных формул арифметической прогрессии;
![]() оценить умения решать ключевые задачи по данной теме;
оценить умения решать ключевые задачи по данной теме;
![]() проверить навыки учащихся по применению своих знаний в ходе решения
нестандартных задач;
проверить навыки учащихся по применению своих знаний в ходе решения
нестандартных задач;
![]() развить представления учащихся об использовании арифметической
прогрессии в окружающей их жизни;
развить представления учащихся об использовании арифметической
прогрессии в окружающей их жизни;
![]() продолжить работу над развитием логического мышления, умением
анализировать, сопоставлять и обобщать полученные знания.
продолжить работу над развитием логического мышления, умением
анализировать, сопоставлять и обобщать полученные знания.
Тип урока: урок-соревнование
Задача учащихся на уроке: устранить проблемы в знаниях.
Методы обучения: словесные, наглядно-иллюстративные, метод эвристической беседы, поисковый метод обучения, групповой метод, метод сотрудничества.
Ход урока
I. Организационный момент
Сегодня мы проведем урок-соревнование между командами. Все члены команды-победительницы получат оценку «5». Победители в личном первенстве также получат «5». Отвечает тот, кто первым поднимет руку.
Учитель. На сегодняшнем уроке вам нужно показать, как вы умеете применять полученные знания при решении задач.
II. Историческая справка (8 мин).
Представление, приветствие команд и домашнее задание.
К оманды
готовили выступление из истории прогрессий.
оманды
готовили выступление из истории прогрессий.
1. Арифметические прогрессии в древности
В клинописных табличках вавилонян, в египетских
пирамидах (П в. до н. э.) встречаются примеры
арифметических прогрессий. Вот пример задачи из
египетского папируса Ахмеса (около 2000 лет до н. э.):
«Пусть тебе сказано: раздели 10 мер ячменя между
10 человеками, разность же между каждым человеком
и его соседом равна ![]() меры.»
меры.»
Вот формула, которой пользовались египтяне:
а = ![]()
А в одном из древнегреческих папирусов приводится следующая задача:
«Имеется 7 домов, в каждом доме по 7 кошек, каждая кошка съедает по 7 мышей, каждая мышь съедает 7 колосьев, каждый из которых, если посеять зерно, дает 7 мер зерна. Нужно посчитать сумму мер зерна».
2. Понятие числовой последовательности возникло и развивалось задолго до создания учения о функциях.
На связь между прогрессиями первым обратил внимание великий АРХИМЕД
(ок. 287-212 гг. до н.э), он вычислял степени числа 10![]() для
нахождения числа песчинок, чтобы целиком заполнить известную в те
времена Вселенную.
для
нахождения числа песчинок, чтобы целиком заполнить известную в те
времена Вселенную.
3 .
Некоторые формулы, относящиеся к прогрессиям, были известны
.
Некоторые формулы, относящиеся к прогрессиям, были известны
китайским и индийским ученым. Например, Ариабхатта (V в.) знал формулы
для общего члена и суммы арифметической прогрессии. Слово «прогрессия»
(лат. progressiо) означает «движение вперед» (как и слово «прогресс»), встречается
впервые у римского автора Боэция. В XVII в., например, Джон Грегорн употребляет
вместо прогрессии термин «ряд»; другой видный английский математик Джон Валлис применяет для бесконечных рядов термин «бесконечные прогрессии».
4. Формула суммы членов арифметической прогрессии была доказана ученым Диофантом (III в.). Правило отыскания суммы членов арифметической прогрессии встречается в «Книге абака» Фибоначчи (1202г.). (Леонардо Пизанский).
В своей книге «Наука о числах» (1484) Н. Шюке дал общее правило для суммирования любой конечной геометрической прогрессии.
5. Сведения, связанные с прогрессиями, впервые встречаются в дошедших до нас документах Древней Греции. Уже в V в. до н. э. греки знали следующие прогрессии и их суммы:
1) 1 + 2 + 3 + … + п = ![]()
2) 2 + 4 + 6 + ... + 2п = п (п + 1).
6. Германия. Гаусс Карл Фридрих
(30.04.1777 - 23.02.1855) - знаменитый немецкий математик родился 30 апреля 1777 г. В раннем детстве он уже обнаружил выдающиеся способности к математике. Около трех лет от роду он уже умел считать и выполнять элементарные вычисления. Однажды, при расчетах своего отца, который был водопроводным мастером, его трехлетний сын заметил ошибку в вычислениях. Расчет был проверен, и число, указанное мальчиком было верно. В 1784г. Карл пошел в школу. Известна ещё одна интересная история о Карле Гауссе. В 7 лет, как и еще сотня таки же мальчиков, он поступил в школу. Поскольку в ней обучались начинающие, никто из мальчиков не слышал об арифметической прогрессии. Учитель дал детям длинную задачу на сложение первых ста натуральных чисел, ответ которой он сам мог найти по формуле за несколько секунд. Через минуту Карл уже решил задачу. Остальные дети пыхтели над задачей целый час. Ему никто не показывал способ решения данного задания и для ребенка найти этот способ мгновенно не так уж и просто. Это открыло Гауссу дверь в науку, через которую он пошел к бессмертию. Среди ученых Карл Гаусс носит имя "Король математики".
7. Список терминов, связанных с именем Гаусса.
Алгоритм Гаусса (вычисления даты пасхи). Гаусс (единица магнитной индукции).
Дискриминанты Гаусса. Гауссова кривизна. Интерполяционная
формула Гаусса. Лента Гаусса.
Малая планета № 1001 (Gaussia). Метод Гаусса (решения систем
линейных уравнений). Метод Гаусса-Жордана. Метод Гаусса-Зейделя.
Нормальное или Гауссово распределение. Прямая Гаусса. Пушка Гаусса.
Ряд Гаусса. Теорема Гаусса - Ванцеля. Фильтр Гаусса.
Формула Гаусса - Бонне.
8. Англия XVIII век. В XVIII в. в английских учебниках появились обозначения арифметической и геометрической прогрессий:
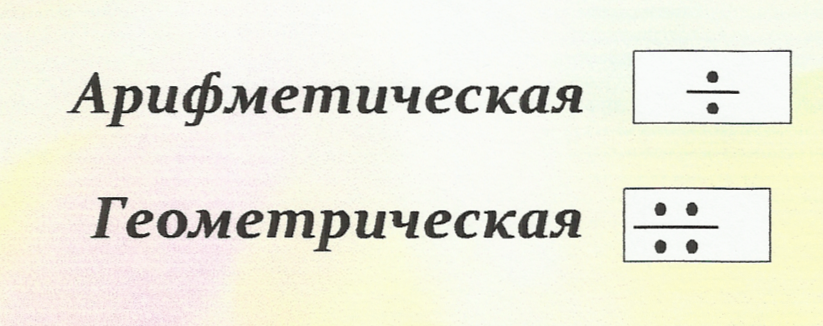
9 .
Задача-легенда (Начало нашей эры.)
.
Задача-легенда (Начало нашей эры.)
Индийский царь Шерам позвал к себе изобретателя
шахматной игры, своего подданного Сету, чтобы наградить его
за остроумную выдумку. Сета, издеваясь над царем, потребовал
за первую клетку шахматной доски 1 зерно, за вторую − 2 зерна,
за третью − 4 зерна и т. д.
Обрадованный царь приказал выдать такую «скромную»
награду. Однако оказалось, что царь не в состоянии выполнить
желание Сеты, так как нужно было выдать количество зерен,
равное сумме геометрической прогрессии
1, 2, 2![]() ,
2
,
2![]() , ...,
2
, ...,
2![]() .
.
Ее сумма равна 2![]() − 1 =
8 446 744 073 709 551 615. Такое количество зерен пшеницы можно
собрать лишь с площади в 2000 раз большей поверхности Земли.
− 1 =
8 446 744 073 709 551 615. Такое количество зерен пшеницы можно
собрать лишь с площади в 2000 раз большей поверхности Земли.
10. В настоящее время мы рассматриваем прогрессии как частные случаи числовых последовательностей.
Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и др.
Команды получают баллы за это задание.
- Теперь нам предстоит повторить тему «Арифметическая прогрессия».
III. Знатоки правил и определений
Члены команд по очереди отвечают на теоретические вопросы по данной теме. Каждая команда отвечает на вопросы. Капитан поручает членам команды отвечать на вопросы.
1. Определение арифметической прогрессии.
2. Примеры арифметической прогрессии.
3. Какое число называют разностью арифметической прогрессии?
4. Свойство членов арифметической прогрессии.
5. Как выражается любой член арифметической прогрессии, начиная со второго, через предыдущий и последующий?
6. Формула п-го члена арифметической прогрессии.
7. Формула суммы п первых членов арифметической прогрессии (I).
8. Формула суммы п первых членов арифметической прогрессии (II).
Если ученик, которому капитан поручил ответить, не знает ответа на вопрос, отвечает команда, но 0,5 балла команда теряет.
Повторение основных формул (3 мин)
1) d = a![]() a
a![]() ; 2)
а
; 2)
а![]() =
а
=
а![]() + (n
-1) d;
+ (n
-1) d; ![]()
3) S![]() =
=![]() 4)
S
4)
S![]() =
=
![]()
Повторение. Разгадать кроссворд.
Вам предстоит разгадать кроссворд. За каждый верный ответ - один балл. В клетке с цифрой букву не пишут, ответы дают в именительном падеже.
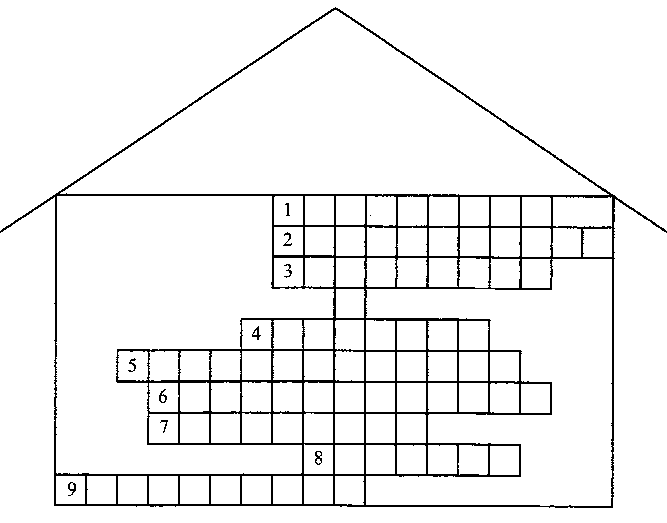
Вопросы:
1. Один из способов задания последовательности. (Описание)
2. Член последовательности стоящий перед любым ее членом, начиная со второго.
(Предыдущий)
3. Последовательность, в которой конечное число членов. (Конечная.)
4. Закончите предложение: «п-й член арифметической прогрессии задается с помощью …
(формулы)».
5 . Название этой формулы в переводе с латинского означает «возвращаться». (Рекуррентная)
6. Последовательность, в которой каждый следующий член больше предыдущего. (Возрастающая)
7. Число, показывающее, на сколько любой член арифметической прогрессии меньше или больше предыдущего. (Разность)
8. Число, указывающее порядковый номер любого члена последовательности. (Индекс.)
9. Последовательность, в которой каждый следующий член меньше предыдущего. (Убывающая.)
-
9
у
б
ы
в
а
ю
щ
а
я
IV. Проверка домашнего задания.
- Внимание на экран. Найдите ошибки, допущенные в домашнем задании, и объясните их. За полный ответ вы получите 2 балла.
1. Найдите первый член и разность арифметической прогрессии
(![]() ),
если
),
если ![]()
Решение: Условия задают систему уравнений: 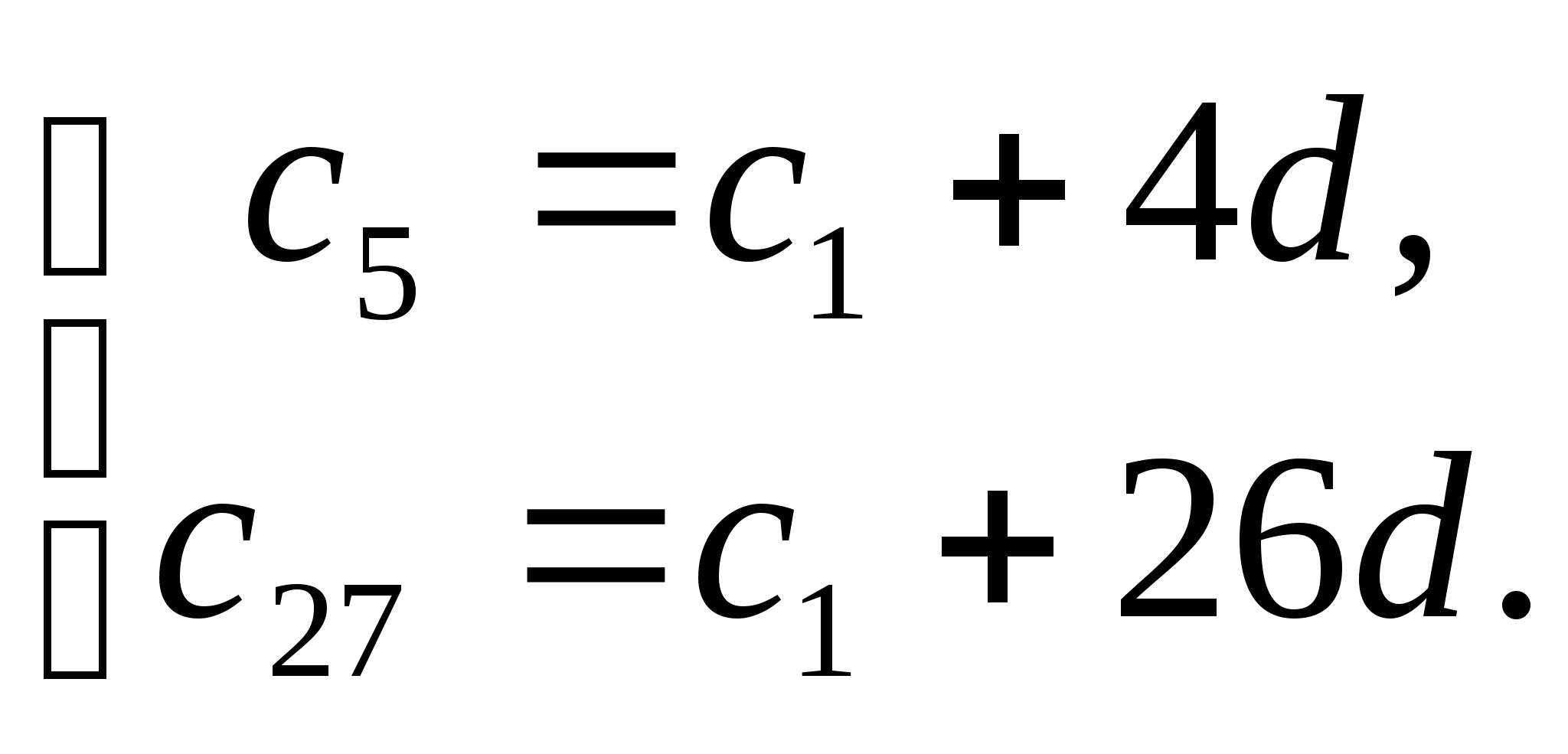
Подставляя данные для ![]() и
и
![]() ,
получаем:
,
получаем: 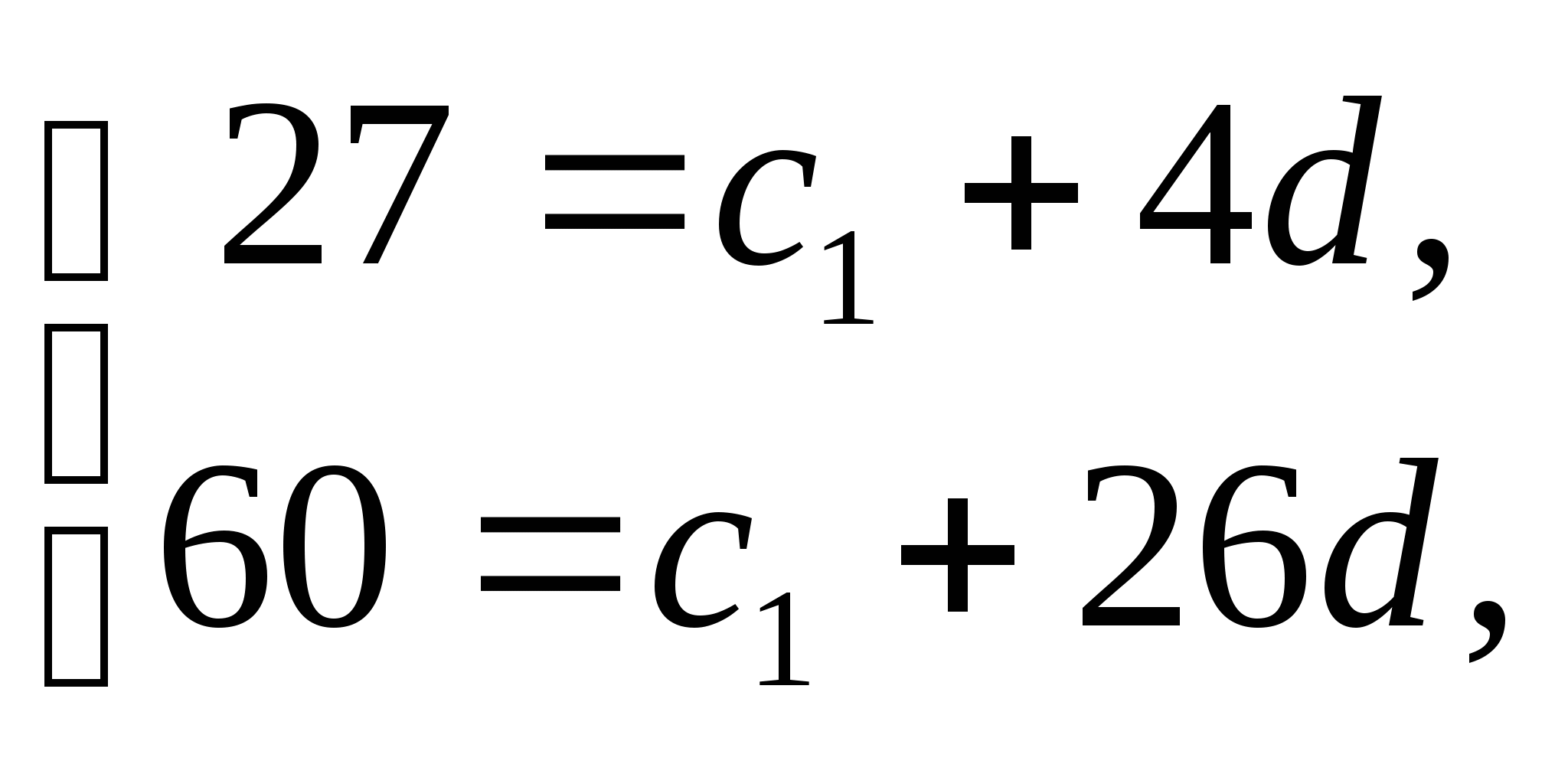 откуда:
откуда:
- 33 = 22d
d = - 1,5
![]() + 4d =
27,
+ 4d =
27,
![]() + 4 ·
1,5 = 27,
+ 4 ·
1,5 = 27,
![]() + 6 =
27,
+ 6 =
27,
![]() = 27
+ 6,
= 27
+ 6,
![]() = 33.
= 33.
Допущенные ошибки: 1) при вычитании 4d - 26d = 22d
потерян знак «-», в результате неверно найдено d; 2) при переносе
слагаемого 6 в выражении ![]() + 6 =
27 потерян знак «-».
+ 6 =
27 потерян знак «-».
Верный ответ: d = 1,5; ![]()
V. Устный счет.
Три сильных ученика - капитаны команд получают карточки индивидуальными заданиями и решения записывают на доске, затем решения закрываются.
А применимы ли прогрессии сейчас?
Карточка №1
Задача. Курс воздушных ванн начинают с 15 мин. в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. Сколько дней следует принимать ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1 час 45 минут?
Дано: (а![]() ) -
арифметическая прогрессия, а
) -
арифметическая прогрессия, а![]() =
15мин, d = 10 мин, а
=
15мин, d = 10 мин, а![]() =
1ч 45 мин = 105 мин.
=
1ч 45 мин = 105 мин.
Найти: п.
Решение: а![]() =
а
=
а![]() +
d ∙(п - 1).
+
d ∙(п - 1).
15 + (п - 1) ∙ 10 = 105,
10 п = 100,
п = 10.
Ответ: 10 дней следует принимать ванны.
Карточка №2
Задача. При хранении бревен строевого леса их укладывают так, как показано на рисунке. Сколько бревен находится в одной кладке, если в ее основание положить 12 бревен?

Дано: (а![]() ) -
арифметическая прогрессия, а
) -
арифметическая прогрессия, а![]() =
12, а
=
12, а![]() =
11, а
=
11, а![]() =
1.
=
1.
Найти: S![]() .
.
Решение: 1) а![]() =
а
=
а![]() +
d ∙(п - 1), где d = а
+
d ∙(п - 1), где d = а![]() -
а
-
а![]() =
1.
=
1.
12 + (-1) ∙ (п - 1) = 1,
12 - п + 1 = 1,
п = 12.
2) Найдем S![]() .
S
.
S![]() =
=
![]() S
S![]() =
=
![]()
Ответ: 78 бревен в одной кладке.
Карточка №3.
Задача. Свободно падающее тело проходит в первую секунду 4,9 м, а в каждую следующую секунду на 9,8 м больше, чем в предыдущую. Найдите глубину шахты, если свободно падающее тело достигло дна шахты через 5 секунд после начала падения.
Дано: (а![]() ) -
арифметическая прогрессия, а
) -
арифметическая прогрессия, а![]() =
4,9м, d = 9,8м, п = 5.
=
4,9м, d = 9,8м, п = 5.
Найти: S![]() .
.
Решение: S![]() =
=
![]() S
S![]() =
=
![]()
Ответ: глубина шахты 122,5 м.
Карточка №4.
Задача. Величины углов выпуклого четырехугольника
образуют арифметическую прогрессию с разностью 42![]() .
Найдите эти углы.
.
Найдите эти углы.
Дано: (а![]() ) -
арифметическая прогрессия, d = 42
) -
арифметическая прогрессия, d = 42![]() , S
, S
![]() =
360
=
360![]() ,
п = 4.
,
п = 4.
Найти: а![]() ,
а
,
а![]() ,
a
,
a![]() , …,
а
, …,
а![]() .
.
Решение: S![]() =
=
![]()
![]() (а
(а![]() +
63) ∙ 4 = 360; а
+
63) ∙ 4 = 360; а![]() +
63 =90;
+
63 =90;
а![]() =
90 - 63 = 27; а
=
90 - 63 = 27; а![]() =
27
=
27![]() ;
а
;
а![]() =
27
=
27![]() +
42
+
42![]() =
69
=
69![]() ;
а
;
а![]() =
69
=
69![]() +
42
+
42![]() =
111
=
111![]() ;
;
а![]() =
111
=
111![]() +
42
+
42![]() =
153
=
153![]() .
.
Ответ: 27![]() ;
69
;
69![]() ;
111
;
111![]() ;
153
;
153![]() .
.
Карточка №5.
Задача. Студенты должны выложить плиткой 288 м![]() .
Приобретая опыт, студенты каждый последующий день, начиная со
второго, выкладывали на 2 м
.
Приобретая опыт, студенты каждый последующий день, начиная со
второго, выкладывали на 2 м![]() больше, чем в предыдущий. И запасов плитки им хватит ровно на 11
дней. Планируя, что производительность труда будет увеличиваться
таким же образом, бригадир определил, что для завершения работы
понадобиться еще 5 дней. Сколько м
больше, чем в предыдущий. И запасов плитки им хватит ровно на 11
дней. Планируя, что производительность труда будет увеличиваться
таким же образом, бригадир определил, что для завершения работы
понадобиться еще 5 дней. Сколько м![]() плитки
уложили в первый день?
плитки
уложили в первый день?
Дано: (а![]() ) -
арифметическая прогрессия, d = 2 м
) -
арифметическая прогрессия, d = 2 м![]() , п
= 11 + 5 = 16, S
, п
= 11 + 5 = 16, S![]() =
288.
=
288.
Найти: а![]() .
.
Решение: S![]() =
=
![]() S
S![]() =
=
![]()
![]()
(а![]() +
15) ∙ 16 = 288; а
+
15) ∙ 16 = 288; а![]() +
15 = 18; а
+
15 = 18; а![]() =
3.
=
3.
Ответ: в первый день выложили 3м![]() .
.
Цель индивидуальных заданий: проверить навыки учащихся при решении задач на применении основных формул арифметической прогрессии. Ученики решают задачи на отдельных листках в течение 5 - 7 мин., пока остальные выполняют проверочную работу.
(Беглый устный счет по карточкам. Одновременно несколько человек из каждой команды работают по карточкам.)
Задание 1. Вычислите. а) - 7 - (- 4,4); б) - 3,1 - (- 4);
в) - 2 - ![]() г)
г)
![]()
д) 3 - 4,2; е) 3 - 2,3;
Ответы: а) - 2,6; б) 0,9; в) - 2![]() ; г) -
11
; г) -
11![]() д) -
1,2; е) 0,7.
д) -
1,2; е) 0,7.
Задание 2. Найдите разность арифметической прогрессии.
а) 3, 7,11,…; б) - 3, - 5, - 7, …; в) 2, 2, 2, …; г) 9, 5, 1, …; д) - 7, - 2, 3, …;
е) ![]() ж) 3,
- 4, - 11, … .
ж) 3,
- 4, - 11, … .
Ответы: а) 4; б) - 2; в) 0; г) - 4; д) 5; е) 0,5; ж) - 7.
Задание 3. Найдите неизвестные члены арифметической прогрессии.
а) с![]() ,
14, с
,
14, с![]() ,
10, с
,
10, с![]() .
.
Решение. с![]()
![]()
Ответ: 16, 14, 12, 10, 8.
б) с![]() ,
с
,
с![]() ,
8, с
,
8, с![]() ,
12.
,
12.
Решение.![]()
Ответ: 4, 6, 8, 10, 12.
VI. Проверка знания учащимися основных понятий и умений объяснять их сущность.
а) Проверка знаний основных формул.
Цель: привлечь к работе «слабых».
На доске (компьютер) формулы с пропусками, ученики дописывают формулы
а![]() =
а
=
а![]() +
(п - 1) ∙ …; S
+
(п - 1) ∙ …; S![]() =
=
![]() а
а![]() =
=
![]() d =
а
d =
а![]() -
…
-
…
Проверка: а![]() =
а
=
а![]() + d
∙(п - 1), S
+ d
∙(п - 1), S![]() =
=
![]()
![]() п ≥
2; d = а
п ≥
2; d = а![]() -
а
-
а![]() .
.
б) Проверка умений пользоваться этими формулами.
На 2 варианта выполняется проверочная работа с кодированным ответом, ключевое слово «Прогрессио».
-
-
Решение:
-
а
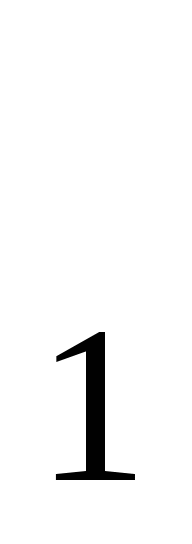 = 6 - 4 = 2;
= 6 - 4 = 2;
6) d = 2 - 6 = -4;
2) а
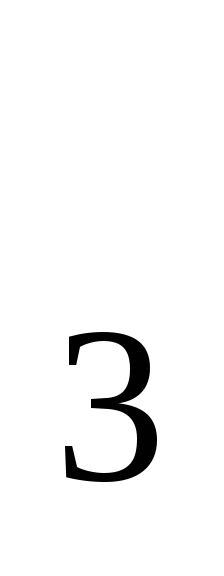 = а
= а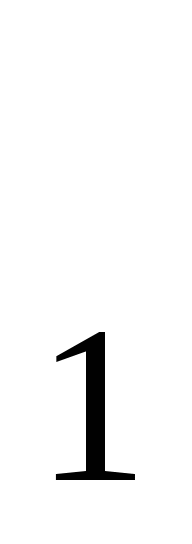 + 2d = 6 + 2∙(-4) = - 2 ;
+ 2d = 6 + 2∙(-4) = - 2 ;
7) d = 6 - 4 = 2;
3) а
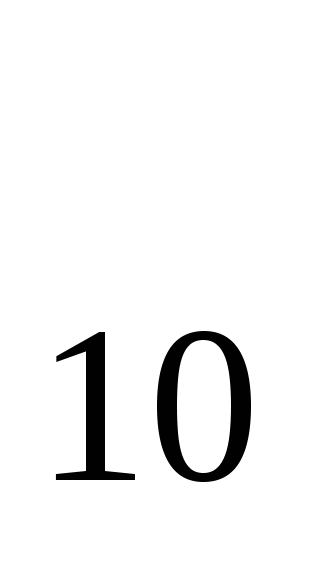 = а
= а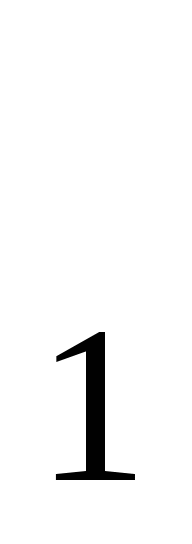 + 9d = 1 + 9·4 = 37;
+ 9d = 1 + 9·4 = 37;
10) а
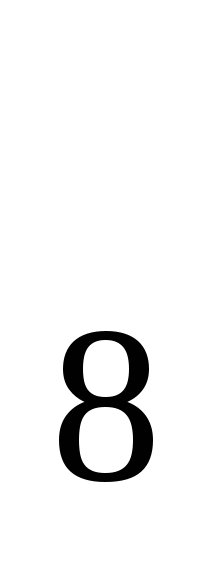 = а
= а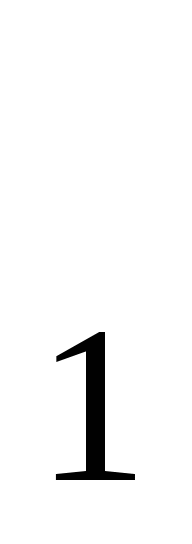 + 7d = 2 + 7·5 = 37;
+ 7d = 2 + 7·5 = 37;
4) S
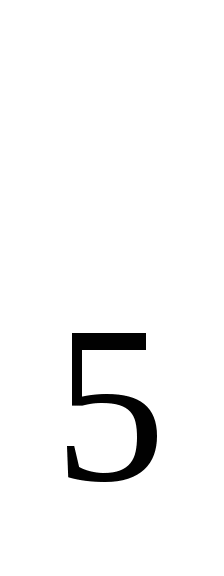 =
= 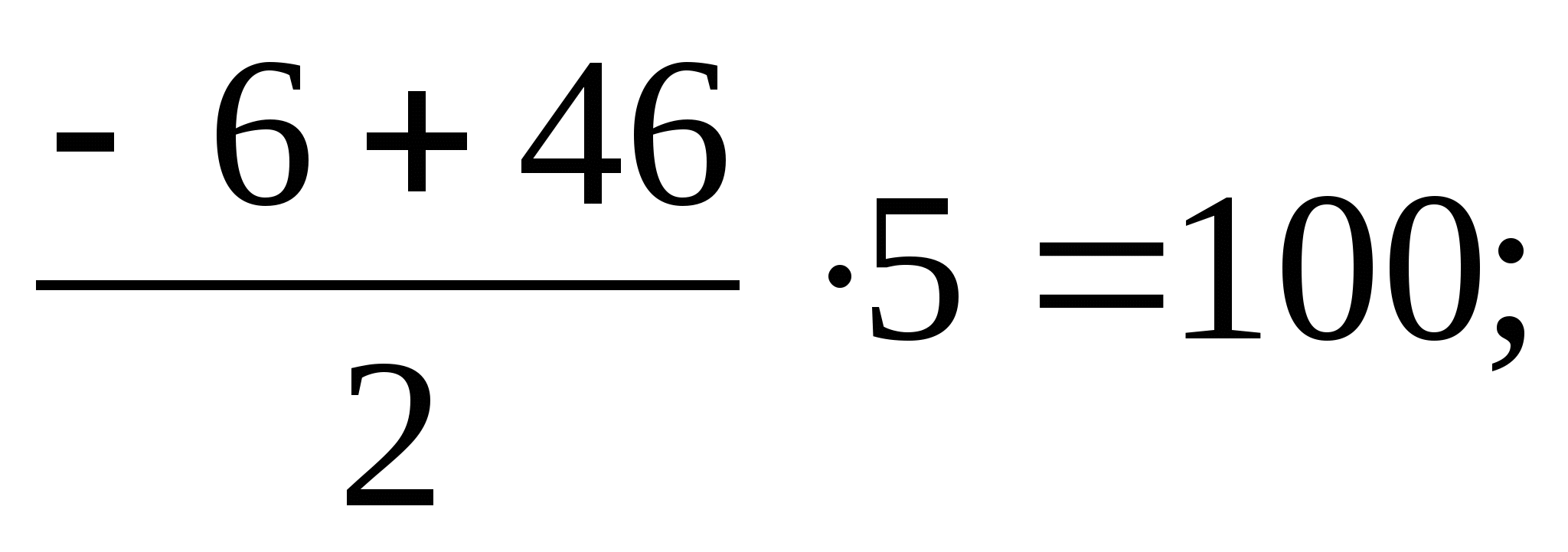
9) S
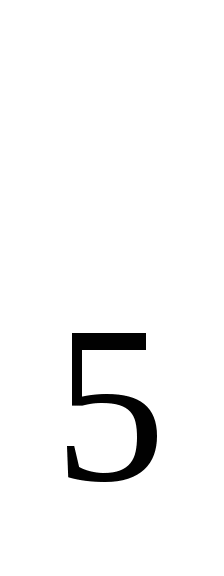 =
= 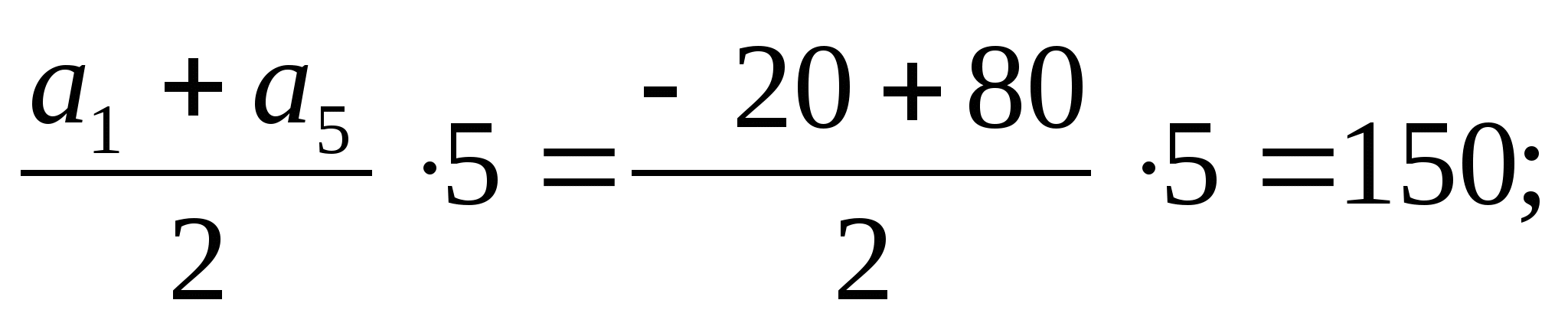
5) а
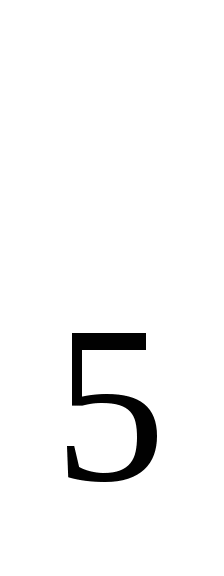 = а
= а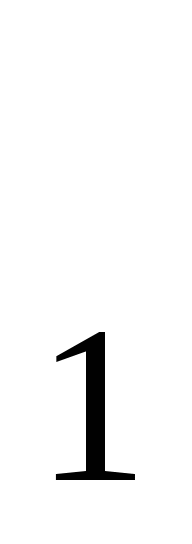 + 4d = 0,2 + 4∙(-0,3) = -1;
+ 4d = 0,2 + 4∙(-0,3) = -1;
S
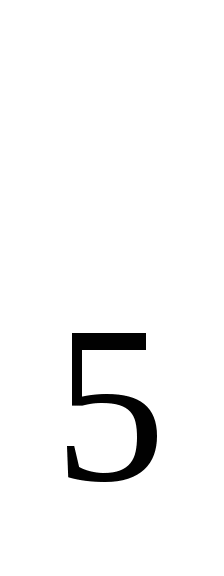 =
= 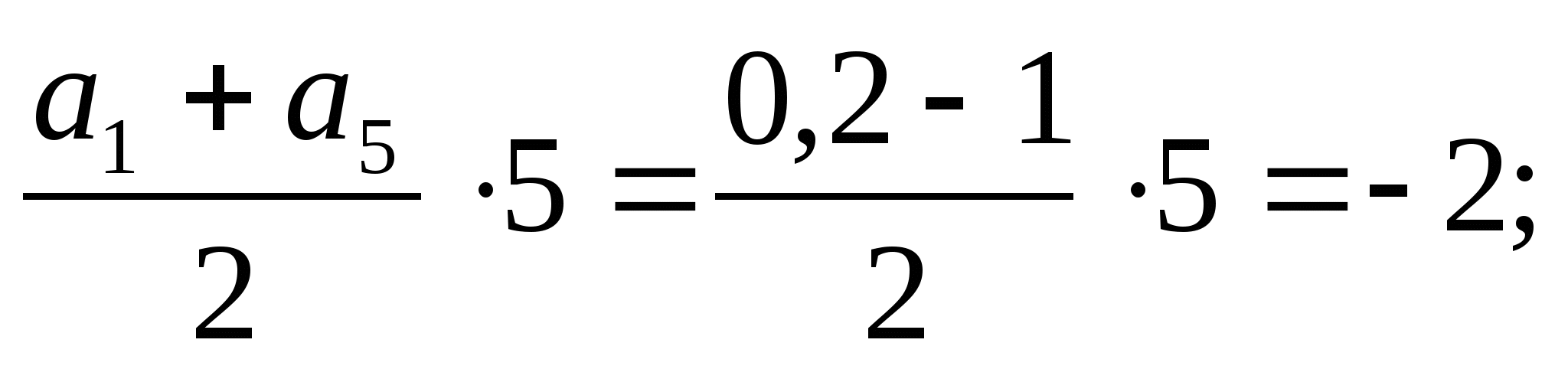
8) а
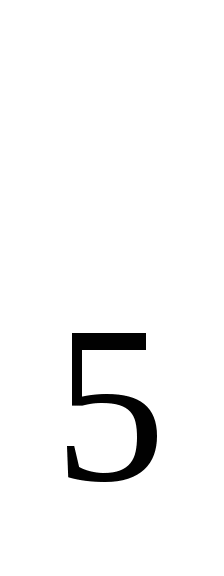 = а
= а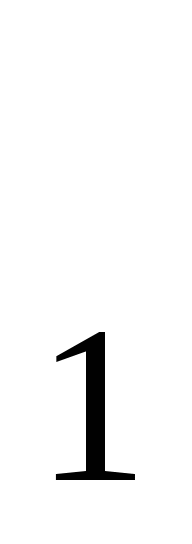 + 4d = 1 + 4∙0,3 = 2,2;
+ 4d = 1 + 4∙0,3 = 2,2;
S
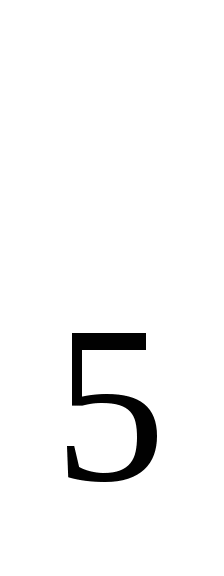 =
= 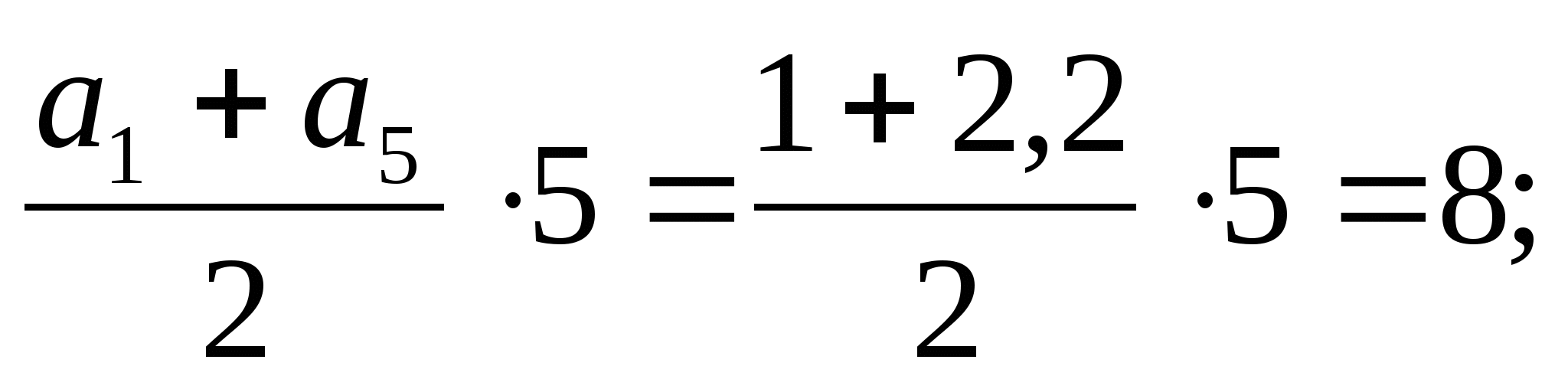
-
а
Проверка данной работы: самоконтроль «+».
VII. Дидактическая игра «Получи пятерку»
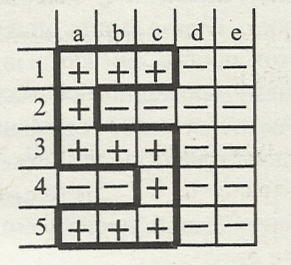
Все вы любите получать пятерки. Сейчас вам представится возможность мгновенно получить «5», для этого нужно принять участие в игре. Заполните таблицу, вписывая в каждую клетку знак «+» или «-». Будьте внимательны. Я буду читать некоторые утверждения. Если вы согласны - пишите «+», если не согласны - пишите «-».
1а. Последовательность, у которой конечное число членов, называется конечной. (+)
1b. Последовательность, у которой бесконечное число членов, называется бесконечной. (+)
1с. Арифметическая прогрессия - это последовательность. (+.)
1d. У возрастающей последовательности второй член меньше первого. (-)
1е. У убывающей последовательности второй член больше первого. (-)
2а. В арифметической прогрессии каждый член, начиная со второго, равен предыдущему, сложенному с одним и тем же числом. (+.)
2b. Последовательность нельзя задать описанием. (-.)
2с. В арифметической прогрессии каждый член, начиная со второго, равен предыдущему, сложенному с различными числами. (-.)
2d. Последовательность не бывает убывающей. (-.)
2е. Никакая последовательность не может быть задана рекуррентной формулой. (-.)
3а. п-й член арифметической прогрессии задается с помощью формулы. (+.)
3b. Чтобы найти разность арифметической прогрессии, надо от любого ее члена отнять предыдущий. (+.)
3с. Чтобы найти п-й член арифметической прогрессии, достаточно знать ее первый член и разность. (+.)
3d. Последовательность натуральных чисел, расположенных в порядке возрастания, не является арифметической прогрессией. (-.)
3е. Последовательность простых чисел является арифметической прогрессией. (-.)
4а. Чтобы найти n-й член арифметической прогрессии, надо из пятого члена вычесть первый.
(-.)
4b. Формула п-го члена арифметической прогрессии а
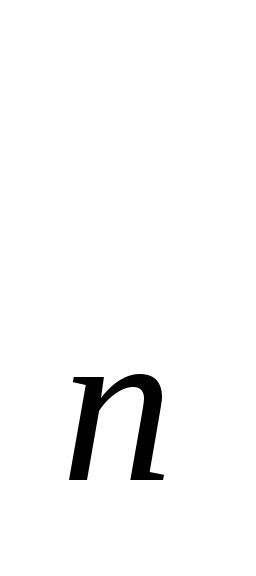 = а
= а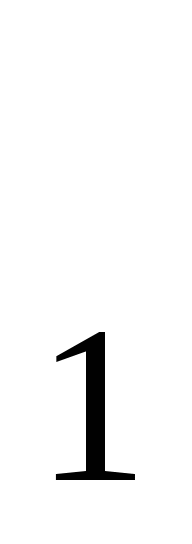 + d
+ d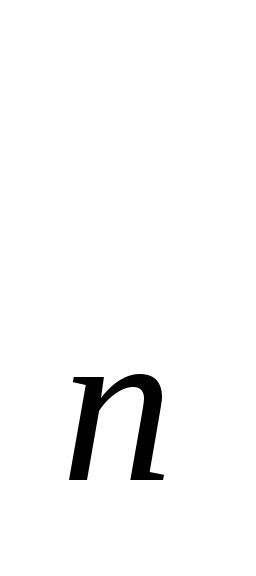 .
(−.)
.
(−.)
4с. Формула п-го члена арифметической прогрессии а
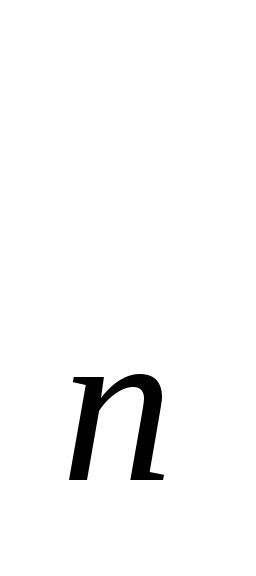 =
а
=
а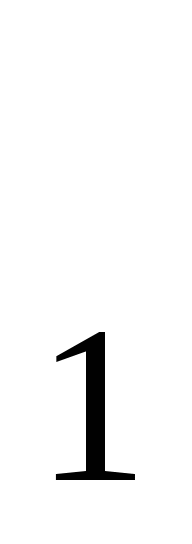 + (п −1)d. (+.)
+ (п −1)d. (+.)
4d. Последовательность положительных четных чисел, расположенных в порядке возрастания, не является арифметической прогрессией. (−.)
4е. Чтобы найти п-й член арифметической прогрессии, надо знать ее любые два члена. (−.)
5а. Последовательность положительных нечетных чисел, расположенных в порядке возрастания, является арифметической прогрессией. (+.)
5b. У возрастающей последовательности каждый следующий член больше предыдущего. (+.)
5с. У убывающей последовательности каждый следующий член меньше предыдущего. (+.)
5d. Для нахождения разности арифметической прогрессии надо знать ее первый и последний члены. (−.)
5е. Разность арифметической прогрессии обозначается а
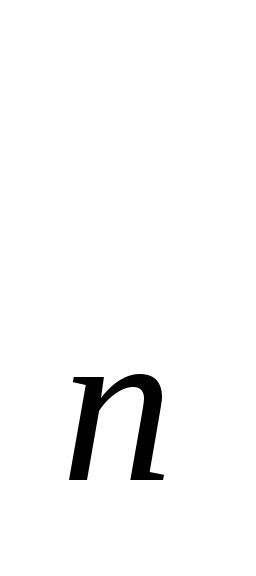 .
(−.)
.
(−.)
− Соедините красным цветом все «+». Что у вас получилось? У кого получилась цифра 5? Вы получаете пятерку!
(Верный ответ проектируется на экран.)
VIII. Подведение итогов урока
(Подведение итогов соревнования.)
Личное первенство: I место − … II место − …
Командное первенство:
I место − … II место − … III место − …
1. В течение урока мы повторили основные формулы арифметической прогрессии.
2. Решали задачи, решение которых облегчает знание формул арифметической прогрессии.Прогрессии мы с вами изучали
И много новых формул вы узнали
Различные задачи прорешали
И вот теперь настал тот час
И вы конечно же должны узнать,
А применимы ли прогрессии в жизни сейчас?
IX. Домашнее задание: а) найти задачи, связанные с арифметической, геометрической прогрессиями из различных областей: физики, медицины и т.д.
Все формулы мы с вами повторили.
Урок успешно завершили.
XI. Интересные факты:
1) Химия. При повышении температуры по арифметической прогрессии скорость химических реакций растет по геометрической прогрессии.
2) Геометрия. Вписанные друг в друга правильные треугольники образуют геометрическую прогрессию. Какие величины в треугольнике образуют геометрическую прогрессию?
3) Физика. И в физических процессах встречается эта закономерность. Нейтрон, ударяя по ядру урана, раскалывает его на две части. Получаются два нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывает их еще на 4 части и т.д. - это геометрическая прогрессия.
4) Биология. Микроорганизмы размножаются делением пополам, поэтому при благоприятных условиях, через одинаковый промежуток времени их число удваивается.
Указать количество бактерий, рожденных одной бактерией за 7 минут.
5) Экономика. Вклады в сбербанке ежегодно увеличиваются на одинаковый процент. Вклад составляет 1000 рублей при 4% годовых. Какую сумму получит вкладчик через 3 года?
6) Литература. Арифметическая прогрессия есть в литературе. Известный стихотворный размер - ямб обладает свойством: ударение ставится на 2, 4, 6, 8, … четные слоги. В то же время хорей: 1, 3, 5, 7… нечетные слоги. Налицо две яркие арифметические прогрессии.
В заключение вспомним строки А. С. Пушкина из романа «Евгений Онегин», сказанные о его герое: «…не мог он ямба от хорея, как мы ни бились, отличить». Ямб - «Мой дядя самых честных правил», то есть ударными являются 2-й, 4-й, 6-й, 8-й и так далее слоги. Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и с разностью, равной двум. Хорей - «Буря мглою небо кроет». Номера ударных слогов также образуют арифметическую прогрессию, но ее первый член равен единице, а разность по-прежнему равна двум: 1,3,5,7, …
Самопроверка знаний
Математический диктант (с самопроверкой) на карточках проводится в виде теста, как подготовка к итоговой аттестации в новой форме.
Математический диктант (с самопроверкой)
на карточках проводится в виде теста, как подготовка к итоговой аттестации в новой форме
1 вариант
1. Первый член арифметической прогрессии 2, разность 4. Укажите ее третий член.
А. 12 Б. 10 В. 8 Г. 14
2. Первый член арифметической прогрессии 5, второй 8. Укажите четвертый член.
А. 13 Б. 16 В. 14 Г. 11
3. Какое из чисел является членом арифметической прогрессии 2; 7; 12; …?
А. 21 Б. 22 В. 26 Г. 25
4. - 4; -1: - арифметическая прогрессия. Число 5 является членом данной арифметической прогрессии. Определите его номер.
А. 4 Б. 5 В. 3 Г. 6
5. Между числами 8 и 14 вставьте такое число, чтобы полученная последовательность чисел образовала арифметическую прогрессию.
А. 13 Б. 10 В. 12 Г. 11
6. Какая из следующих последовательностей может являться арифметической прогрессией?
А. 2; 4; 8; 16;… Б. -5; 5; -5; 5; … В. 1; 3; 5; 7; … Г. 1; 4; 9; 16; …
2 вариант
1. Первый член арифметической прогрессии 1, разность 3. Укажите ее третий член.
А. 9 Б. 6 В. 8 Г. 7
2. Первый член арифметической прогрессии 3, второй 7. Укажите четвертый член.
А. 15 Б. 16 В. 14 Г. 13
3. Какое из чисел является членом арифметической прогрессии 4; 10; 16; :?
А. 27 Б. 28 В. 29 Г. 30
4. - 6; -2: - арифметическая прогрессия. Число 6 является членом данной арифметической прогрессии. Определите его номер.
А. 5 Б. 6 В. 3 Г. 4
5. Между числами 7 и 13 вставьте такое число, чтобы полученная последовательность чисел образовала арифметическую прогрессию.
А. 9 Б. 10 В. 11 Г. 12
6. Какая из следующих последовательностей может являться арифметической прогрессией?
А. 1; 4; 9; 16; … Б. 3; -3; 3; -3; … В. 5; 3; 1; -1; -3;… Г. 1; 8; 27; 64; …
3 вариант
1. Первый член арифметической прогрессии 5, разность 4. Укажите ее третий член.
А. 12 Б. 11 В. 13 Г. 14
2. Первый член арифметической прогрессии 6, второй 3. Укажите четвертый член.
А. -3 Б. -2 В. -1 Г. 1
3. Какое из чисел является членом арифметической прогрессии 7; 11; 15; :?
А. 37 Б. 34 В. 36 Г. 35
4. - 8; -5;: - арифметическая прогрессия. Число 4 является членом данной арифметической прогрессии. Определите его номер.
А. 4 Б. 5 В. 3 Г. 6
5. Между числами 9 и 17 вставьте такое число, чтобы полученная последовательность чисел образовала арифметическую прогрессию.
А. 11 Б. 12 В. 13 Г. 14
6. Какая из следующих последовательностей может являться арифметической прогрессией?
А. 2; 4; 8; 16; … Б. -6; 6; -6; 6; … В. 1; 2; 4; 7; … Г. 4; 1; -2; -5; …
4 вариант
1. Первый член арифметической прогрессии 3, разность 5. Укажите ее третий член.
А. 13 Б. 12 В. 11 Г. 10
2. Первый член арифметической прогрессии 4, второй 1. Укажите четвертый член.
А. -3 Б. -4 В. -5 Г. -6
3. Какое из чисел является членом арифметической прогрессии 3; 8; 13; :?
А. 38 Б. 37 В. 36 Г. 35
4. - 7; -3: - арифметическая прогрессия. Число 9 является членом данной арифметической прогрессии. Определите его номер.
А. 4 Б. 6 В. 3 Г. 5
5. Между числами 7 и 15 вставьте такое число, чтобы полученная последовательность чисел образовала арифметическую прогрессию.
А. 10 Б. 11 В. 12 Г. 13
6. Какая из следующих последовательностей может являться арифметической прогрессией?
А. -2; 2; -2; 2; … Б. 5; 2; -1; -4; … В. 5; 3; 0; -4; … Г. 1; 8; 14; 19; …
Ответы к математическому диктанту заносятся учащимися в бланки ответов, которые перед самопроверкой сдаются учителю. Для самопроверки учащиеся дублируют свои ответы в тетрадях.
Бланк ответов к математическому диктанту:
-
Фамилия ______________ Вариант ___
Ответы:
1.
2.
3.
4.
5.
6.
-
Самопроверка осуществляется с помощью компьютера.
Ответы к математическому диктанту:
-
1 вариант
Ответы:
1. Б
2. В
3. Б
4. А
5. Г
6. В
2 вариант
Ответы:
1. Г
2. А
3. Б
4. Г
5. Б
6. В
3 вариант
Ответы:
1. В
2. А
3. Г
4. Б
5. В
6. Г
4 вариант
Ответы:
1. А
2. В
3. А
4. Г
5. Б
6. Б
</