Конспект урока по математике Сравнение целых чисел (6 класс)

Ход урока:

1). Организационный момент (слайд 1)

Приветствие;

Проверка готовности учащихся к уроку.

- Сегодня мы с вами познакомимся с новыми понятиями: положительные и отрицательный числа, модуль числа, правила сравнения двух рациональных чисел.

2). Актуализация знаний. Повторение пройденного материала.

Фронтальный опрос:

- Какую тему изучали на предыдущих уроках?

Положительные и отрицательные числа, координатная прямая, модуль числа, противоположные числа.

- Какую цель будем ставить перед собой?

Повторить положительные и отрицательные числа; определение координатной прямой; изображение точек на координатной прямой; модуля числа; нахождение модуля; противоположных чисел.

Повторим положительные и отрицательные числа (слайд №2)

- Приведите примеры положительных чисел.

- Приведите примеры отрицательных чисел.

- Чем отличаются друг от друга положительные и отрицательные числа?

- Что можно сказать про число 0?

- Как можно назвать все целые числа и все дроби?

Письменно на листочках (слайд № 3).

1. Из чисел 28; -17; 0; 21; -6 выпишите:

а) положительные числа;

б) отрицательные числа;

в) число, которое не относится ни к положительным, ни к отрицательным.

Проверить и подвести итог (слайд № 4):

Ответы:

а) 28; 21;

б) -17; -6;

в) 0.

• 5 "+" отметка 5,

• 4 "+" отметка 4 ,

• 3 "+" отметка 3.

Повторим про координатную прямую (слайд № 5).

- Дайте определение координатной прямой.

Письменно на листочках:

2. а) Запишите координаты отмеченных точек.

б) Отметьте на координатной прямой точки М(4); N(-3,5); Р(2,5);К(-2).

Проверить и подвести итог (слайд № 6):

Ответы:

а) А(-2); В(1,5);

С(5); D(-4,5); О(0);

б)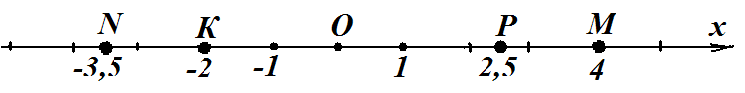

• 9 "+" отметка 5,

• 8-7 "+" отметка 4 ,

• 5-6 "+" отметка 3.

Повторим о противоположных числах, модуле числа (слайд № 7).

- Дайте определение противоположных чисел и приведите примеры.

- Что называется модулем числа а?

- Чему равен модуль положительного числа? Пример.

- Чему равен модуль отрицательного числа? Пример.

- Чему равен модуль 0?

Письменно на листочках (слайд № 8).

3. а) Запишите точки, которые имеют противоположные координаты.

б) Из данных чисел -2,6; 2,05; 2,2; -2,22; 2,53 выберите то, которое имеет наибольший модуль.

в) Вычисли: |-4|1,5; 34 - |- 16|; |+23|+|-8|.

Проверить и подвести итог (слайд № 9):

Ответы:

а) А(-3) и В(3);

б) -2,6;

в) 6; 18; 31.

• 5 "+" отметка 5,

• 4 "+" отметка 4 ,

• 3 "+" отметка 3.

Подведите итог своей работы, оцените себя.

Рефлексия:

- Кто думает, что материал предыдущих уроков усвоил хорошо?

- Кто считает, что надо ещё поработать над этим материалом?

- Кто удовлетворён своими результатами?

3). Изучение нового материала.

Учащимся предлагается записать число и тему урока в тетрадь: "Сравнение чисел" (слайд № 10).

- Знакома ли вам тема сегодняшнего урока?

- Какие числа мы умеем сравнивать?

Натуральные числа, десятичные и обыкновенные дроби.

Устно: сравнить числа :

• 15 и 28;

• 13 и 8;

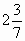• и ;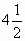

• 12 и 11;

• -8 и 6.

- Почему мы не можем сравнить последнюю пару чисел?

- Как называются эти числа?

- Все ли числа мы умеем сравнивать?

- Тогда сформулируйте цели и задачи урока (учитель может их записать на доске).

Решить последний пример поможет нам координатная прямая (слайд № 11). Замечаем, что по мере "продвижения" вправо от точки О положительные числа увеличиваются, а по мере "продвижения" влево к точке О числа уменьшаются до нуля. Сделайте вывод о расположении больших положительных чисел и меньших положительных чисел на координатной прямой.

• Из двух положительных чисел больше то, которое на координатной прямой расположено правее, меньше то - которое левее.

Во всех случаях правее на координатной прямой расположено большее число, левее - меньшее. Следовательно, для отрицательных чисел на координатной прямой, сохраняется тот же порядок, что и для положительных. Учащимся предлагается сформулировать правило рациональных чисел и записать его в тетрадь.

• Из двух рациональных чисел больше то, которое на координатной прямой расположено правее, меньше то - которое левее.

Теперь мы сможем сравнить последнюю пару чисел и объяснить почему.

4. Физкультминутка.

5. Закрепление изученного материала (слайд № 12).

1. Устно:

• № 233-236

2. Письменно:

• № 238, 240(а-е) - на доске и в тетрадях.

• № 239 - самостоятельно с последующей проверкой

Проверить и подвести итог (слайд № 13):

Ответы:

№ 238:

а) 5 > 0; в) 7 > 0; д) 8 > -7;

б) -5 < 0; г) -7 < 0; е) -3 < 100.

№ 240(а-е):

а) 728 < 800; в) -999 < 2; д) 725 > 0;

б) -296 < 1; г) 0 > -500; е) -600 < -5.

• все "+" отметка 5,

• 1-2 "-" отметка 4 ,

• 3 "-" отметка 3.

3. Выполните тест в тетради (слайд № 14).

1) Из двух целых чисел больше то, которое в ряду целых чисел расположено -

а) правее; б) левее.

2) Какое из чисел -3 и -12 на координатной прямой расположены правее числа -7:

а) -3; б) -12.

3) Сравнить модуль чисел -23 и 15:

а) >; б) <; в )=.

4) Сколько чисел расположено на координатной прямой между числами -3 и 1:

а) 0; б) 3; в )5; г) -3.

5) Какие из чисел -7 и 10 на координатной прямой расположены левее числа -6.

а) -7; б) 10; в) другой ответ.

Проверить и подвести итог:

Ответы:

1. а;

2. а;

3. а;

4. б;

5. а.

• 5 "+" отметка 5,

• 4 "+" отметка 4 ,

• 3 "+" отметка 3.

6. Домашнее задание (слайд № 15).

• Выучить правила на стр. 50;

• № 241 - 243;

• *Объясните с помощью ряда неотрицательных чисел, почему если для целых чисел a, b, c верны неравенства a > b и b > c, то верно неравенство a > c.

7. Подведение итогов (каждый учащийся выставляет себе оценку за работу на уроке).

Учитель оценивает работу учащихся на уроке и выставляет оценки, собирает тетради.