Урок по геометрии 'Пять красивых тел' (о правильных многогранниках 11 класс)

Чульчаева Эльза Шорваевна

Почетный работник общего образования

Российской Федерации

Тема урока:

«ПЯТЬ КРАСИВЫХ ТЕЛ ».

( о правильных многогранниках)

Цели урока:

1) обучающая:

систематизировать, обобщить, углубить знания, отработать навыки учащихся по теме: «Правильные многогранники»;

2) развивающая:

• развивать умения самостоятельно оценивать собственные знания;

• стимулировать деятельность учащихся к поиску новых знаний;

3) воспитательная:

• повысить интерес учащихся к изучаемой теме;

• воспитание многогранной, духовно развитой личности.

Ход урока:

/Видеосюжет/

Итак, тема сегодняшнего урока «Пять красивых тел». Мы должны выполнить следующую работу: (цели, задачи)

Эпиграфом к нашему уроку станут слова Л.Кэрролла:

Правильных многогранников вызывающе мало,

но этот весьма скромный по численности

отряд сумел пробраться в самые глубины

различных наук.

Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники, они всегда восхищали пытливые умы симметрией, простотой и мудростью своих форм.

Ребята, перед вами лежат модели многогранников. Выберите из них правильные. Как вы определили что они правильные? Сколько их?

Существует всего пять видов правильных многогранников. Вот они перед вами. Почему не существует правильного многогранника гранями, которого являются правильный шестиугольник, семиугольник? При каждой вершине многогранника должно быть не менее 3^х плоских углов. У правильного шестиугольника один угол равен , а три угла в вершине это 360⁰, это невозможно, т.к. сумма плоских углов < 360⁰, т.е. для правильных многогранников не существует.

Изучая любые многогранники, естественнее всего подсчитать, сколько у них граней, сколько ребер и вершин. Подсчитаем и мы число указанных элементов.

Обратите внимание на то, что на каждом столе лежат листы фиолетового и желтого цветов с заданиями. По мнению психологов, фиолетовый и желтый цвета активизируют интеллектуальную деятельность.

Таблица 1

Правильный многогранник

Число

Граней

Г

Вершин

В

Ребер

Р

Тетраэдр

4

4

6

Куб

6

8

12

Октаэдр

8

6

12

Додекаэдр

12

20

30

Икосаэдр

20

12

30

- Нет ли закономерности в возрастании чисел в каждом столбце?

Можно рассмотреть сумму чисел в двух столбцах, хотя бы в столбцах «грани» и «вершины»

Таблица 2

Правильный многогранник

Число

Граней и вершин

Г + В

Ребер

Р

Тетраэдр

4 + 4 = 8

6

Куб

6 + 8 = 14

12

Октаэдр

8 + 6 = 14

12

Додекаэдр

12 + 20 = 32

30

Икосаэдр

20 + 12 = 32

30

«Сумма числа граней и вершин равна числу ребер, увеличенному на 2».

Г + В = Р + 2

Итак, мы вместе «открыли» формулу, которая была подмечена уже Декартом в 1640 г, а позднее переоткрыта Эйлером (1752), имя которого с тех пор она и носит.

Эйлер 31 год посвятил России. А вы знаете, что 2008 год объявлен годом Эйлера? В мае в Элисте будет подведен итог по году Эйлера.

Домашнее задание состоит из двух частей:

1).Подберите несколько значений Г, В, Р, удовлетворяющих формуле Эйлера.

Для тех, кто особенно заинтересовался, есть еще одно задание.

2). Уважаемые ребята, постарайтесь изобразить этот многогранник.

И.Кеплер высказал такое замечание: «Среди правильных тел самое первое, начало и родитель остальных - куб, а его, если позволительно так сказать, супруга - октаэдр, ибо у октаэдра столько углов, сколько у куба граней».

Между правильными многогранниками есть двойственность. Центры граней одного служат вершинами другого и обратно. Тетраэдр двойственен тетраэдру. Октаэдр - кубу, и куб - октаэдру. Икосаэдр - додекаэдру, и додекаэдр - икосаэдру. Поэтому, построив додекаэдр, можно по центрам его граней построить икосаэдр.

А сейчас с помощью компьютера мы изобразим многогранники и увидим красоту двойственных тел.

1. Практическая работа на компьютерах/технологическая карта компьютерного эксперимента/

Релаксация./звучит музыка, учащиеся по развертке собирают правильный многогранник/

Уважаемые одиннадцатиклассники! Я прошу вас попытаться собрать многогранники по данной развертке. Прошу вас отнестись к этой работе достаточно серьезно, т.к. она, на мой взгляд, поможет вам немного отвлечься, но и вместе с тем результат деятельности - собранный многогранник - вернет вас к теме сегодняшнего разговора…

Спасибо, заканчиваем. Внимание, домашнее задание.

Домашнее задание: Склеить правильный многогранник по данной развертке.Для тех, кто особенно заинтересовался вычислить площадь поверхности и объем многогранника.

А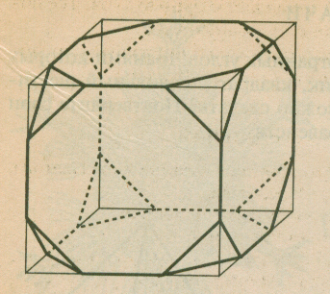 сейчас решим задачу, которая относится к третьей части ЕГЭ.

Задача: От куба отсечены 8 правильных треугольных пирамид плоскостями, проходящими через точки, делящие ребра куба на три равные части. Ребро куба равно а. Найдите объем оставшейся части куба.

Итак, ребята, мы узнали о двойственности правильных многогранников, провели компьютерный эксперимент, а теперь будет интересно узнать где встречаются правильные многогранники в природе.

Правильные многогранники - самые выгодные фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых кристаллов. Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она хорошо растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли (NaCl) имеют форму куба.

При производстве алюминия пользуются алюминиево - калиевыми квасцами (K[Al(SO₄)₂]12H₂O), монокристалл которых имеет форму правильного октаэдра.

Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра. В разных химических реакциях применяется сурьменистый сернокислый натрий (Na₅(SbO₄(SO₄)) - вещество, синтезированное учеными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.

Последний правильный многогранник - икосаэдр передает форму кристаллов бора (В). В свое время бор использовался для создания полупроводников первого поколения.

Правильные многогранники встречаются и в живой природе. Например, скелет одноклеточного организма феодарии по форме напоминает икосаэдр. Чем же вызвана такая природная геометризация феодарий? Тем, по-видимому, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объем при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.

Дорогие ребята! Прежде чем перейти к следующему этапу нашего урока, я хочу чтобы вы посмотрели еще один любопытный, на мой взгляд, видеосюжет.

Видеосюжет /Ступа Просветления/

«28 июля 1998 года в торжественной обстановке была открыта Ступа Просветления. Ступа Просветления в Элисте представляет собой величественное сооружение высотой 11метров. Каждая деталь монумента имеет свое символическое значение, так, квадратное основание символизирует землю, круглая часть - Бумба - стихию воды, золотые кольца - огонь, зонт - корона - воздух, капля на луне и солнце символизирует эфир, или пустоту - пятый элемент, из которого возникли четыре элемента жизни».

Как вы заметили, что каждая деталь Ступы имеет форму геометрической фигуры. И мне остается добавить, что Ступа Просветления - это действующее культовое сооружение, которое должно защищать Калмыкию, способствовать всяческому процветанию и дарить неисчислимые блага всем окружающим.

А теперь мы вернемся к правильным многогранникам.

Правильные многогранники иногда называют Платоновыми телами, поскольку они занимали видное место в философской картине мира, разрабатываемой великим мыслителем Древней Греции Платоном (ок.428 - ок.348 до н.э.)

Платон считал, что мир строится из четырех «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырех правильных многогранников. Итак, тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр - как самый обтекаемый - воду; куб - самая устойчивая из фигур - землю, а октаэдр - воздух. В наше время эту систему можно сравнить с четырьмя состояниями вещества - твердым, жидким, газообразным и плазменным. Пятый многогранник - додекаэдр - воплощал в себе «все сущее», символизировал весь мир и почитался главнейшим.

Я надеюсь, что этот видеосюжет не оставил у вас сомнений в том, что тела, о которых мы сегодня говорили действительно обладают особой красотой. Итак, о чем же мы говорили сегодня? Спасибо за урок!

Технологическая карта компьютерного эксперимента

шаги

действия

СОЗДАТЬ СЕТКУ

Выбрать в меню Графики/показать узлы сетки

Выбрать в меню Графики/спрятать оси.

На панели инструментов выбрать инструмент ЛИНИЯ

ИЗМЕНЕНИЕ СТИЛЯ И ЦВЕТА ЛИНИИ

А) Выбрать в меню Вид команду Стиль линии

Б) Выбрать в меню Вид команду Цвет линии

ПОСТРОЕНИЕ КУБА

Используя инструмент Линия, построить куб с длиной стороны 8 единиц.

Внимание: соблюдайте пунктирные линии. Для этого, после построения всех линий выбрать инструмент Выделения на панели инструментов и указав на линию изменить стиль линии.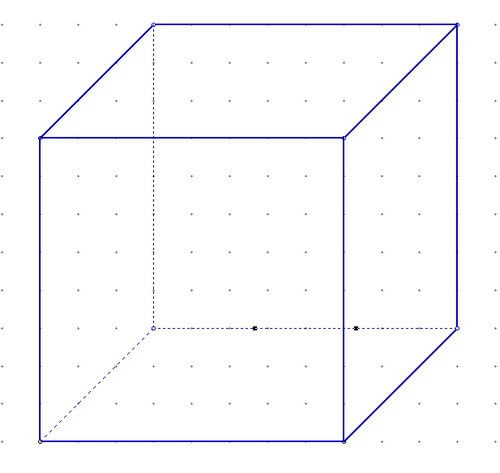

П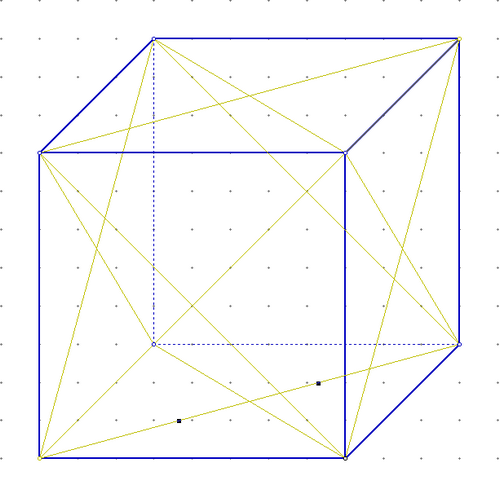ОСТРОЕНИЕ ДИАГОНАЛЕЙ ГРАНЕЙ

Н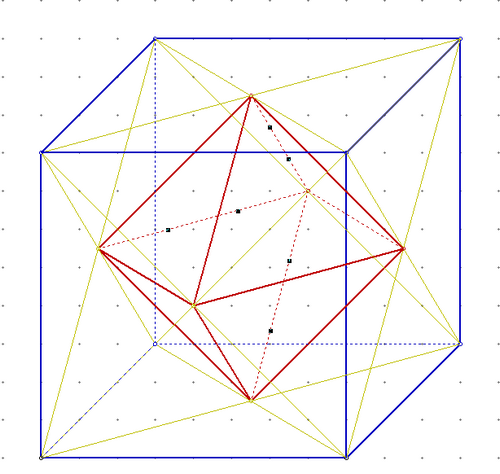а каждой из 6 граней построить диагонали.

Соединить точки пересечения диагоналей.

В результате получим

Октаэдр вписанный в куб .

Задания к уроку

1. Заполнить таблицу:

Таблица 1

Правильный многогранник

Число

Граней

Г

Вершин

В

Ребер

Р

Тетраэдр

Куб

Октаэдр

Додекаэдр

Икосаэдр

Таблица 2

Правильный многогранник

Число

Граней и вершин

Г + В

Ребер

Р

Тетраэдр

Куб

Октаэдр

Додекаэдр

Икосаэдр

З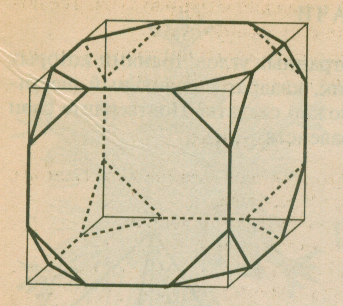адача: От куба отсечены 8 правильных треугольных пирамид плоскостями, проходящими через точки, делящие ребра куба на три равные части. Ребро куба равно а. Найдите объем оставшейся части куба.

Домашнее задание.