Разработка урока на тему 'Решение неравенств методом интервала'

Тема: «Решение неравенств методом интервалов».

План-конспект проведения урока. Алгебра 9 класс.
Тема. «Решение неравенств методом интегралов».
Тип урока: комбинированный.

Цели и задачи урока:

образовательные - ввести алгоритм решения неравенств методом интервалов, формировать навыки применения этого алгоритма в нестандартных ситуациях;
развивающие - развивать логическое мышление, способность самостоятельно решать учебные задачи;
воспитательные - прививать интерес к предмету, знакомить с медиаресурсами на уроках математики, развивать сознательное восприятие учебного материала
Оборудование:
-мультимедийный проектор;
-компьютер с необходимым программным обеспечением.

Ход урока.

1.Организационный момент.

2.Проверка домашнего задания.

3.Введение нового материала.

4. Решение задач на закрепление.

5.Дифференцированная самостоятельная работа.

6. Домашнее задание (краткие комментарии по выполнению). 7.Подведение итогов.

Ход урока.

1.Организационный момент. Презентация используемая на уроке выполнена в программе Microsoft Offise Power Point 2003.Работает по щелчку.

Слайды: Сообщение темы и цели урока.

Учитель: «Но прежде чем мы перейдём к нашей новой теме, давайте все вместе повторим прошлую тему. Для этого сейчас пойдут к доске следующие ученики для решения примеров из домашнего задания, а остальные ребята будут отвечать на мои вопросы.

2.Проверка домашнего задания:

четверо учащихся решают на доске № 116 (а, б, в, г);

Весь класс отвечает на вопросы учителя:

1. Какой вид имеет полное квадратное уравнение? (ах² + вх + с = 0)

2. Сколько корней имеет квадратное уравнение, если Д > 0? (2к)

Д < 0?(корней нет); Д = 0? (1к)

3. Назовите виды неполных квадратных уравнений (если в = 0, то ах² + с = 0; если с = 0, то ах² + вх = 0)

4. Теперь давайте повторим расположение графиков квадратичной функции:

а) Сначала скажите мне, как называется график квадратичной функции? (парабола);

б) Куда направлены ветви параболы, если: а > 0?(вверх); а <0?(вниз)

в) Сколько точек пересечения с осью абсцисс имеет парабола если при решении квадратного уравнения Д > 0? (2 точки); Д < 0? (нет точек пересечения ); Д = 0? (1точка).

3.Введение нового материала.

Рассмотрим функцию

f(х) = (х+2)(х-3)(х-5)

1. Областью определения этой функции является множество всех чисел: Д(f)=(- ∞;+∞)

2. Найдём нули функции:

х + 2 = 0 х - з = 0 х - 5 = 0

х = - 2 х = 3 х = 5

Они разбивают область определения на промежутки:

(- ∞; - 2), (-2; 3), (3; 5), (5; +∞)

Выражение (х+2)(х-3)(х-5) представляет собой произведение трёх множителей. Рассмотрим знак множителей на каждом исследуемом промежутке:

(- ∞; - 2)

(-2; 3)

(3; 5)

(5; +∞)

х + 2

-

+

+

+

х - з

-

-

+

+

х - 5

-

-

-

+

Произведение знаков

-

+

-

+

f(х) < 0

f(х) > 0

f(х) < 0

f(х) > 0

(Рисунок промежутков)

А теперь давайте разберём с вами конкретный пример:

Пример № 1. Решить неравенство (х+6)(х+1)(х-4) <0

Рассмотрим функцию f(х) =(х+6)(х+1)(х - 4)

1. Область определения данной функции Д(f)=(- ∞;+∞)

2. Найдём нули данной функции: х + 6 = 0; х + 1 = 0; х - 4 = 0.

х = - 6 х = - 1 х = 4

Определяем промежутки и знаки функции в каждом из них:

(- ∞; - 6)

(-6; -1)

(-1; 4)

(4; +∞)

х + 6

-

+

+

+

х + 1

-

-

+

+

х - 4

-

-

-

+

Произведение знаков

-

+

-

+

f(х) < 0

f(х) > 0

f(х) < 0

f(х) > 0

(Рисунок промежутков)

Решением данного неравенства является выбор промежутков, на которых функция принимает отрицательные значения. (f(х) < 0)

Ответ: х (- ∞; - 6) (-1; 4)

Учитель: «И ещё один момент, на который вам ребята необходимо обратить своё внимание: при решении неравенств методом интервалов, так же как и при решении любого вида неравенств, необходимо определить вид неравенства: строгое оно или нет. Давайте заполним следующую таблицу:

Строгое неравенство

Нестрогое неравенство

знаки

«» или « > »

« » или « »

скобки

Круглые

Квадратные

точки

Не закрашенные « ° »

Закрашенные « • »

4. Решение задач на закрепление. Работа у доски и в тетрадях Закрепление навыков в решении неравенств методом интервалов.
Работаем по учебнику «Алгебра 9». (двое учащихся)
№ 136 (в, г). Найдите множество решений неравенства.
в). (х+12)(3-х)>0
Решаем, используя алгоритм.
Выделим функцию f(х) = (х+12)(х-3)

1. Найдём D (?)= R

2. Нули функции (х+12)(х-3)=0

х = -12; х=3

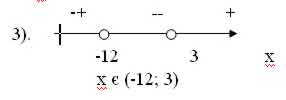
Ответ: х (-12; 3)

г). (6+х)(3х-1) 0

Решаем, используя алгоритм:
Выделим функцию
f(х) =(х+6)(3х-1)

1). Найдём D(?) = R
2).Нули функции (х+6)(х-1)=0
х₁ = - 6; х₂ =

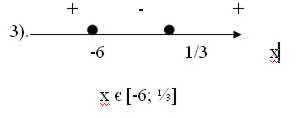
Ответ: [-6; ] .

5. Самостоятельная работа.

Самостоятельная работа проводится на листочках 7 минут. После выполнения самостоятельной работы учащимся предлагается записать ответы в тетрадь и сдать работы. Затем на слайде изображаются ответы для самопроверки.