Урок математики в 11 классе по теме Применение производной в исследовании функций

Муниципальное казённое общеобразовательное учреждение

«Средняя общеобразовательная школа №3 г.Облучье» имени Героя Советского Союза Юрия Владимировича Тварковского

УРОК-семинар

«Применение производной к исследованию функции»

11 класс

Разработала: учитель математики высшей квалификационной категории Кузнецова О.С.

2012 г

Урок-семинар по теме

«Применение производной к исследованию функций»

Урок-семинар «Применение производной к исследованию функций», завершающий изучение данной темы, является повторительно-обобщающим. Целью его проведения было и систематизировать и обобщить знания учащихся по теме, научить каждого старшеклассника мыслить и оперировать математическими знаниями, определяемыми документами стандарта не оставив при этом без внимания старшеклассников которым математика интересна как наука, требующая полета фантазии и оригинальности мышления.

На данном занятии был подведен итог по теме: «Применение производной к исследованию функции». Вопросы теории были подготовлены группами учащихся. Стандартный учебный материал был расширен проектной работой, выходом которой являлась презентация по теме «Нахождение множества значений наибольшего и наименьшего значений функций», нацеливающая выполнять эти задания с использованием монотонности функции.

Все задания семинара, начиная с подготовительного этапа, были составлены с учетом дифференциации и индивидуализации. Естественно, что материал, выходящий за рамки программы, разрабатывали учащиеся с ярко-выраженными познавательными потребностями.

Данный урок отличался от стандартного большей степенью самостоятельности учащихся, их высокой активностью, владением навыков работы с литературой, изменением организации этапов обучения. На первых этапах работы над темой «производная и ее применение» учащимся было сообщено, что итогом обучения будет не только контрольная работа, но и двухчасовой семинар.

Учащиеся прошли все этапы подготовки к семинару: подобрали литературу, получили консультации учителя, использовали рекомендации с алгоритмами «как работать с литературой», «как написать тезисы к докладу».

Учителем были разработаны дифференцированные задания рецензирование докладов, рекомендации по их оформлению.

Семинар помог раскрыть творческие способности учащихся.

Каждый ученик получил по 3 оценки за подготовку к семинару, за решение практических задач, за ответы на вопросы блиц-турнира, который был предложен в конце занятия.

Таким образом, учащиеся систематизировали знания по теме «Применение производной», а так же, не выходя за рамки учебника, познакомились с более рациональным, в некоторых случаях, способом определения множества значений функции с использованием монотонности. Данные знания помогут учащимся справиться с заданиями ЕГЭ.

Цели урока:

1. Обобщить и систематизировать знания учащихся по теме «Производная. Применение производной».

2. продолжить формирование у учащихся потребность мыслить, развивать свои способности.

3. Воспитывать чувство достоинства и взаимоуважения.

Оборудование: проектор, экран, готовые презентации, задания к блиц-турниру, оформленные в виде презентации.

Технологии: технология проектного обучения; информационно-коммуникационные технологии; технология проблемного обучения.

Ход урока

1. Подготовительный период.

1. Класс заранее разбивается на 6 групп (по уровню математических способностей).

2. За 6 уроков до семинара учащимся сообщаются задания, по которым каждая группа разрабатывает проект. Темы, предлагаемые для проектов:

а) Историческая справка.

б) Физический смысл производной.

в) Геометрический смысл производной.

г) Исследование и построение графиков функций.

д) Решение текстовых задач на экстремум.

е) Применение монотонности к исследованию функции на наибольшее и наименьшее значения.

Кроме проектных работ учащиеся выполняют практическую часть по общей теме.

Практическая часть домашнего задания.

Задания на «3».

1. Закон прямолинейного движения материальной точки задан зависимостью S(t) = 5t³ - 8t + 2, где S и t измеряются соответственно в метрах и секундах. Найти скорость и ускорение в момент времени t = 2с.

Ответ: 52 м/сек; 60 м/с².

2. Найти тангенс угла наклона касательной к графику функции у = х³ - 3х в точке М (0;0).

Ответ: - 3.

3. Составить уравнение касательной к графику функции у = х² - 2х + 5 в очке М (4; 13).

Ответ: у = 6х - 11.

4. Исследовать функцию и построить ее график у = х⁴ - 8х² + 8.

5. Найти наибольшее и наименьшее значения функции у = 12х - х³ на отрезке [- 1; 3].

Ответ. (16 и -11)

Задания на «4».

1. Вращение тела вокруг оси совершается по закону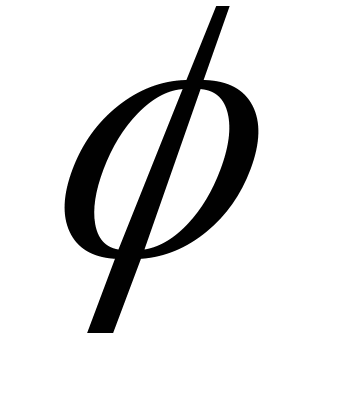(t)=2t² - 4t + 3. Найти угловую скорость W (t) рад/с вращения тела в момент времени t = 4 с.

Ответ: 12 рад/с.

2. Определить угол, который составляет с осью Ох касательная к графику функции у = 2х² в точках с абсциссами х₀ = 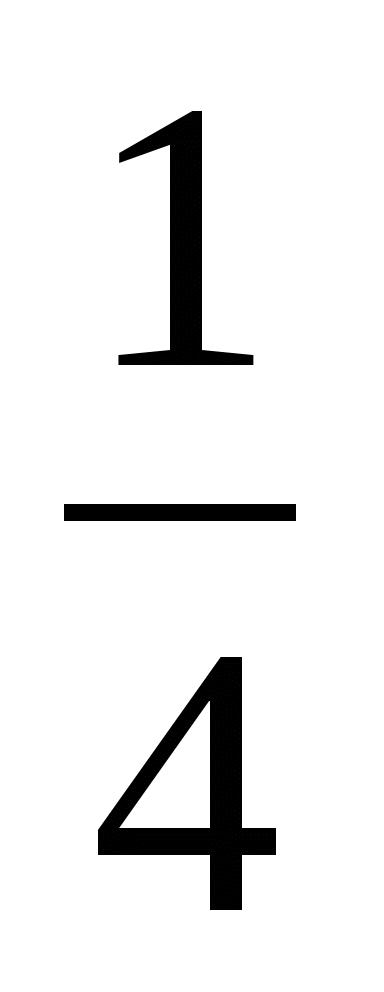и х₀ = 1.

Ответ: 45⁰; arctg 4.

3. Определите промежутки возрастания и убывания функции: f (t) = sin x - 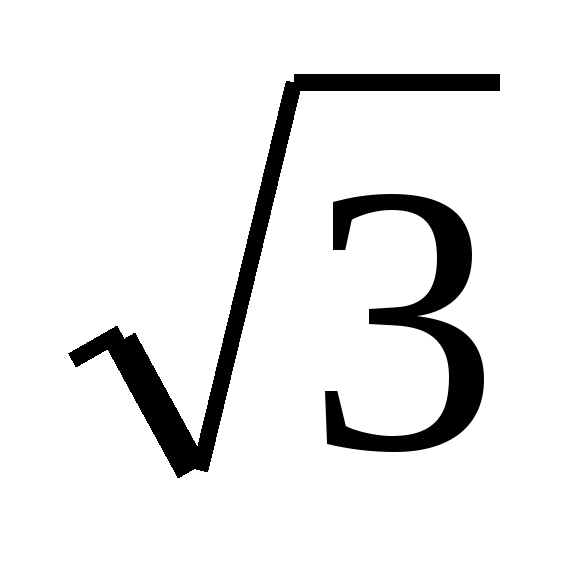cos x - x.

Ответ: убывает на [ + 2к; 2 + 2к],

возрастает на [2к; + 2к].

4. Исследуйте функцию на возрастание, убывание, экстремумы и постройте ее график f (х) = .

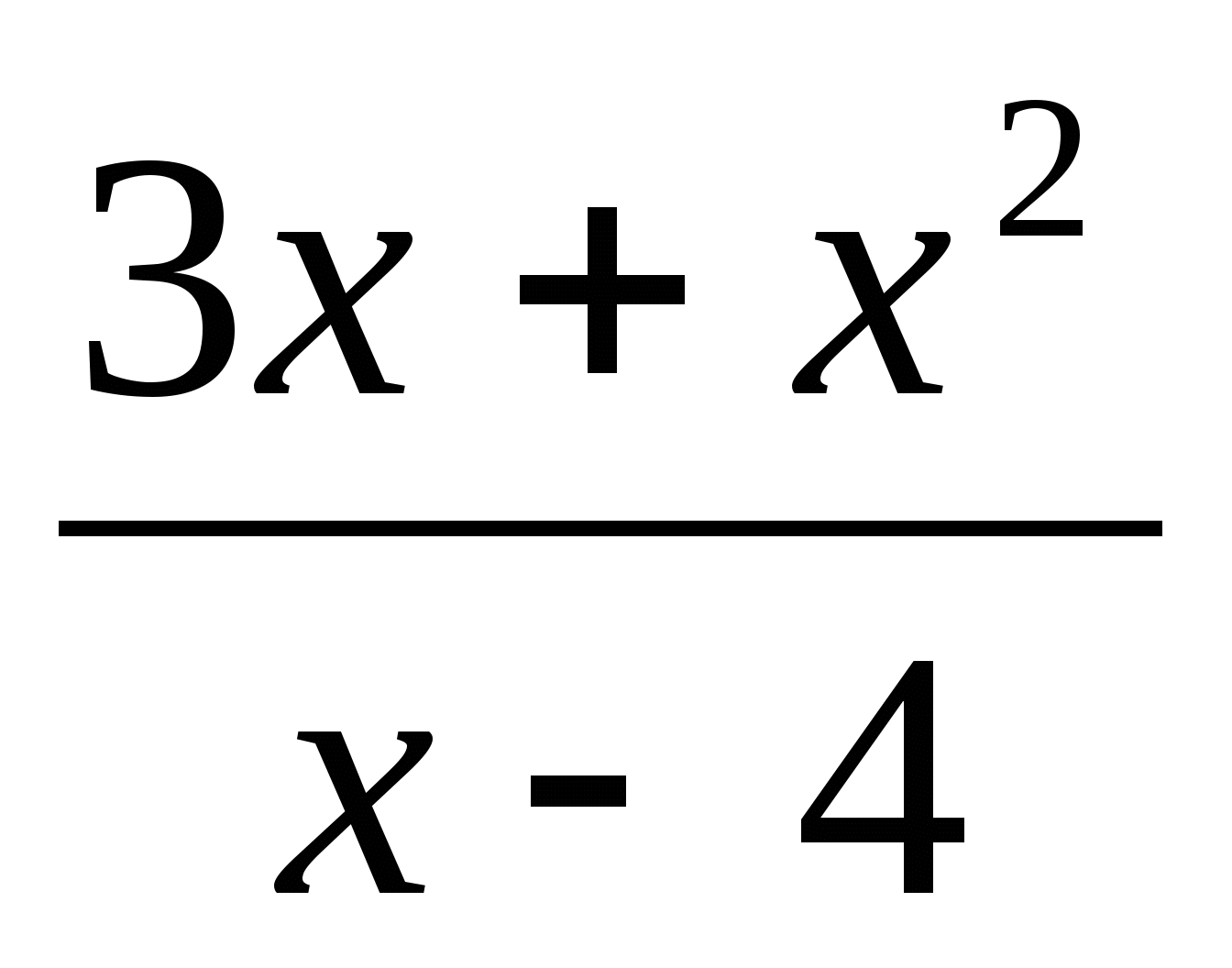5. Найти наибольшее и наименьшее значения функции у = 2х³ + 3х² + 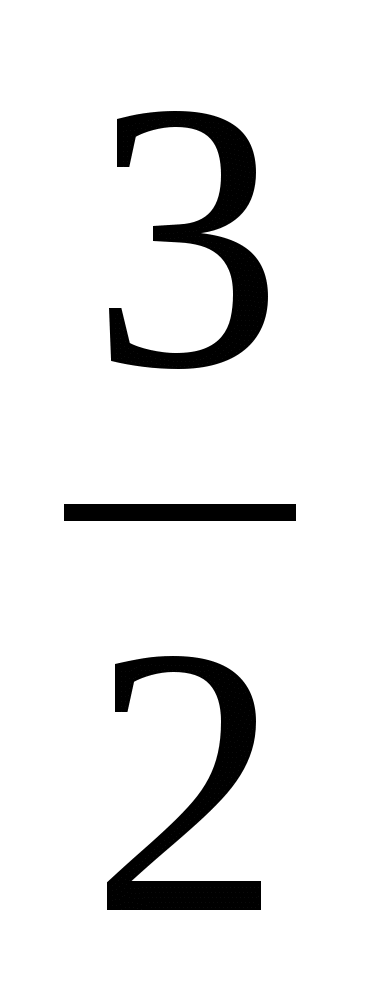х + 30 на отрезке [- 3; 3].

Ответ: 115,5 и - 1,5.

Задания на «5».

1. Существует ли производная в точке х = 0 у следующих функций?

а) у = х Ответы: а) нет

б) у = б) да

в) у = в) да

2. В каких точках касательная к графику функции у = 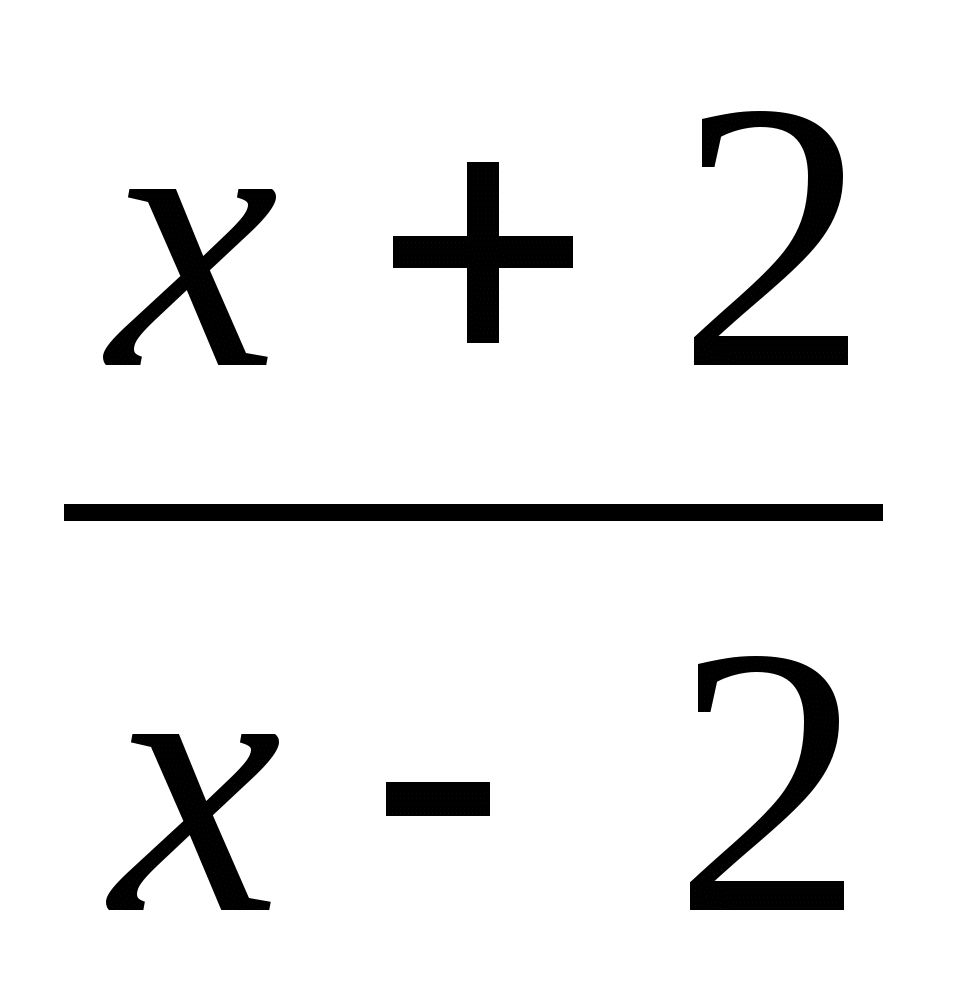образует с осью Ох угол в 135⁰?

Ответ: (о; - 1), (4; 3).

3. Под каким углом пересекается с осью Ох кривая у = ?

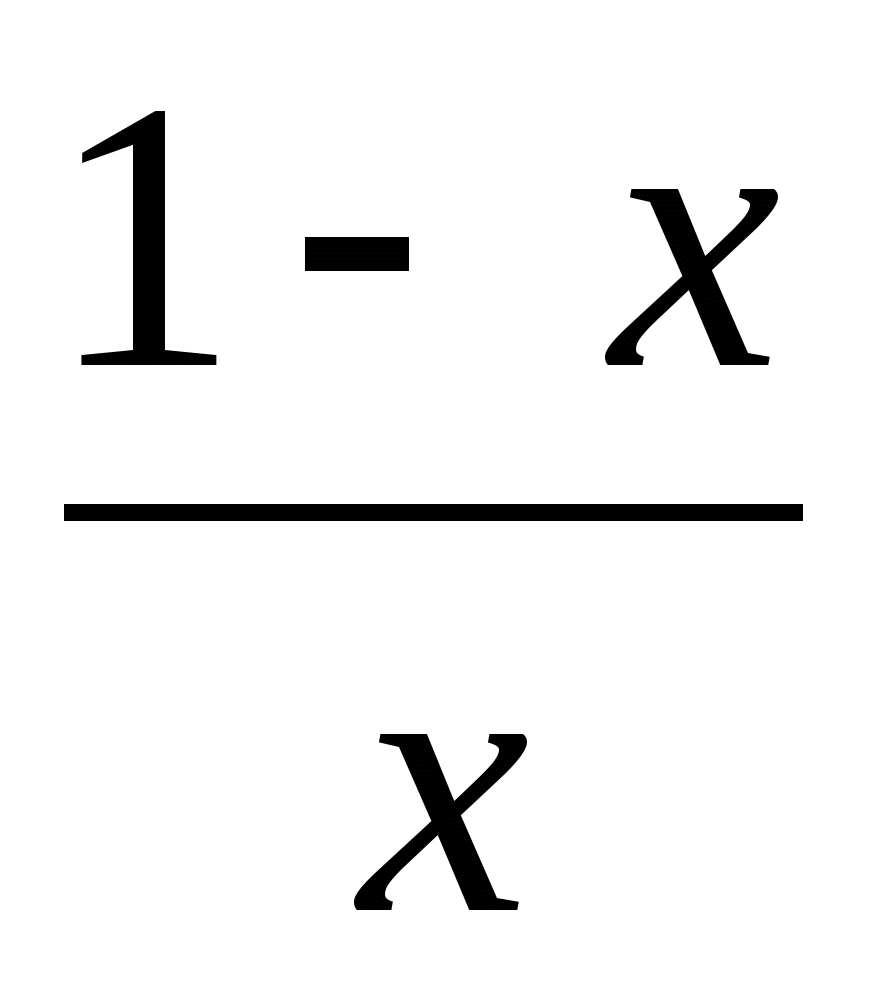Ответ: у = - 2х.

4. Исследуйте функцию на возрастание, убывание, экстремумы и постройте ее график f (х) = 2 + .

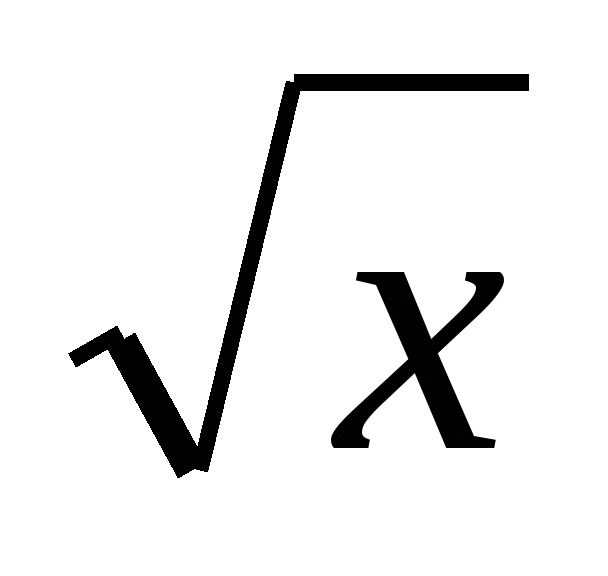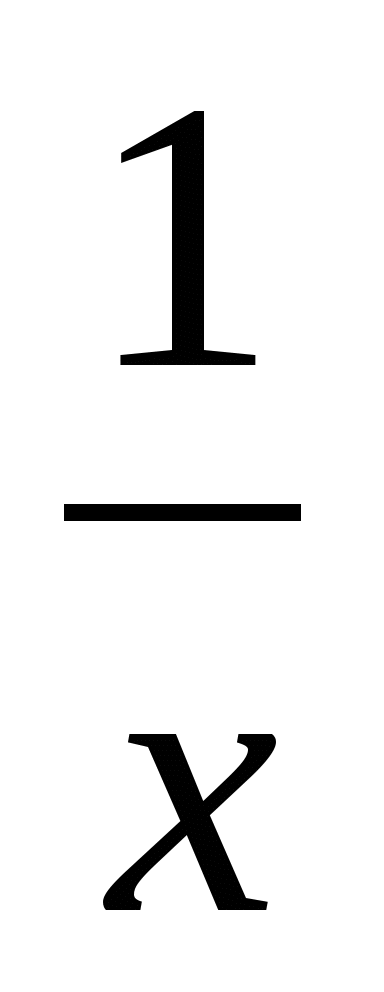5. Найти наибольшее и наименьшее значения функции у = 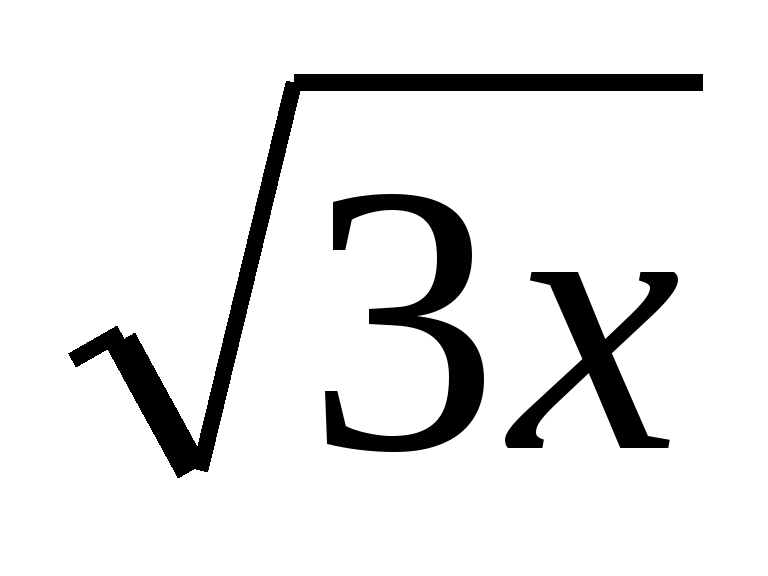+ sin 2x, на отрезке [0; ].

Ответ: и 0.

2. Организационный момент.

Учитель сообщает тему, цель урока. Учащиеся сидят по группам за столами, которые стоят таким образом, чтобы учащиеся могли видеть доску, экран проектора.

3. Актуализация опорных знаний.

Пять представителей от каждой группы готовятся у доски, излагая одну из задач, подобранных из различных учебных пособий и отвечают на вопросы:

1. Геометрический смысл производной.

2. Физический смысл производной.

3. Роль знака производной для определения возрастания и убывания функции на некотором промежутке.

4. Дать определение касательной, проведенной к графику функции. Записать уравнение касательной.

5. Нахождение наибольшего и наименьшего значений сложной функции с помощью монотонности.

Пока они готовятся, все учащиеся просматривают презентацию по исторической справке, делая соответствующие записи в тетрадях, а также презентацию «Применение монотонности при нахождении множества значений наибольшего и наименьшего значений функции». Заслушав план решения каждой задачи, записанной на доске, учащиеся делают вывод о том, что наиболее ёмкое применение производная находит при решении различных задач на исследование функции и построение графиков функций.

4. Решение задач по теме.

а) Учащиеся со слабой подготовкой (I, II группы) выполняют задания:

1. Вычислить производную функций:

а) у = х³ - 3х + - 5. Ответ: у´ = 3х² - 3 - .

б) у = sin x - 4 cos x + 6 e^x. Ответ: у´ = cos x + 4 sin x + 6 e^x.

в) у = (7х - 1)¹⁰⁰. Ответ: у´ = 707 · (7х - 1)⁹⁹.

2. Найти угловой коэффициент касательной к графику функции у = х³ - 3х² - 6х - 1 в точке с абсциссой х₀ = - 2. Ответ: 18.

3. Найти интервалы возрастания и убывания функции, точки экстремума у = 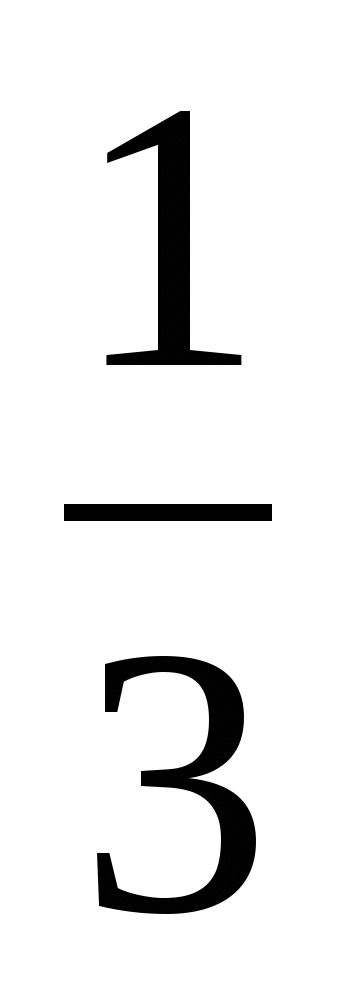х³ - х² - 3х + 5.

Ответ: f (x) , если х (- ; - 1] [3; + )

f (x) , если х [- 1; 3].

- 1 - точка max; 3 - точка min.

б) Учащиеся со средними способностями (III, IV группы) выполняют задания:

1. Найти f´(2), если f(x) = 4 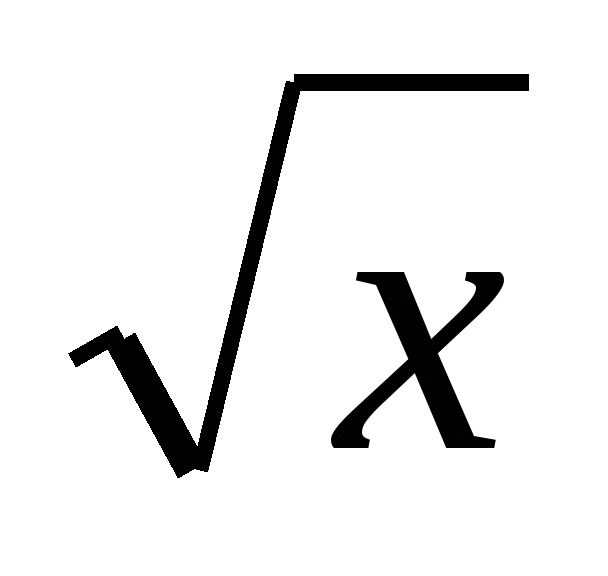- 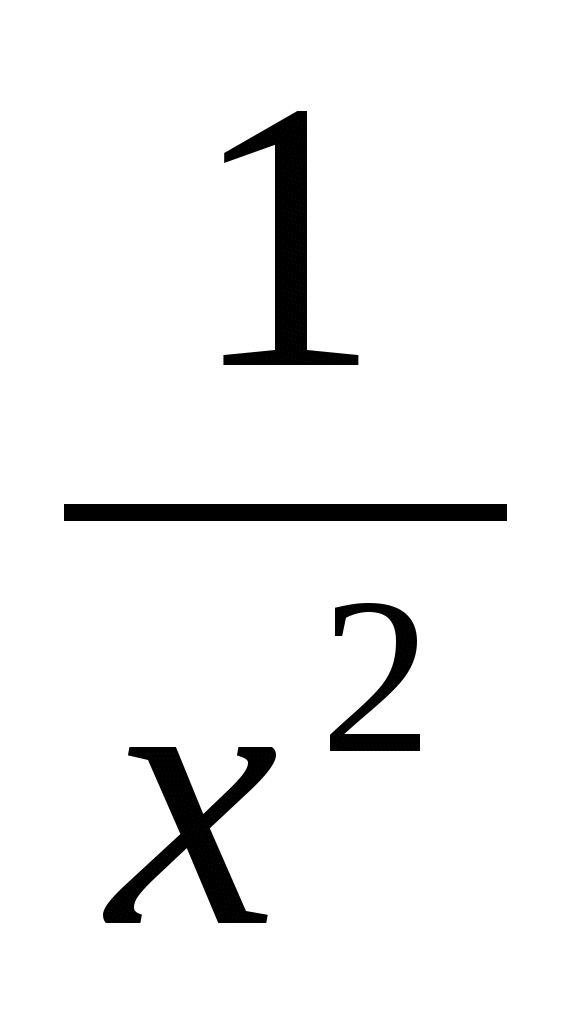+ 2х². Ответ: f´(2) = 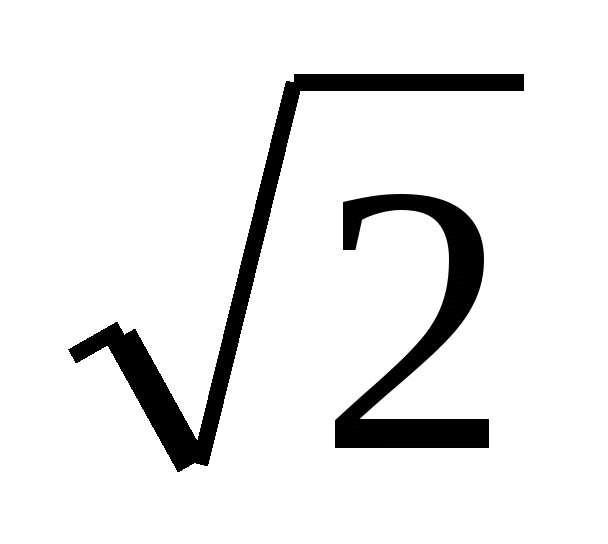+ 8,25.

2. Решить неравенство f´(х) > 0, если f (x) = 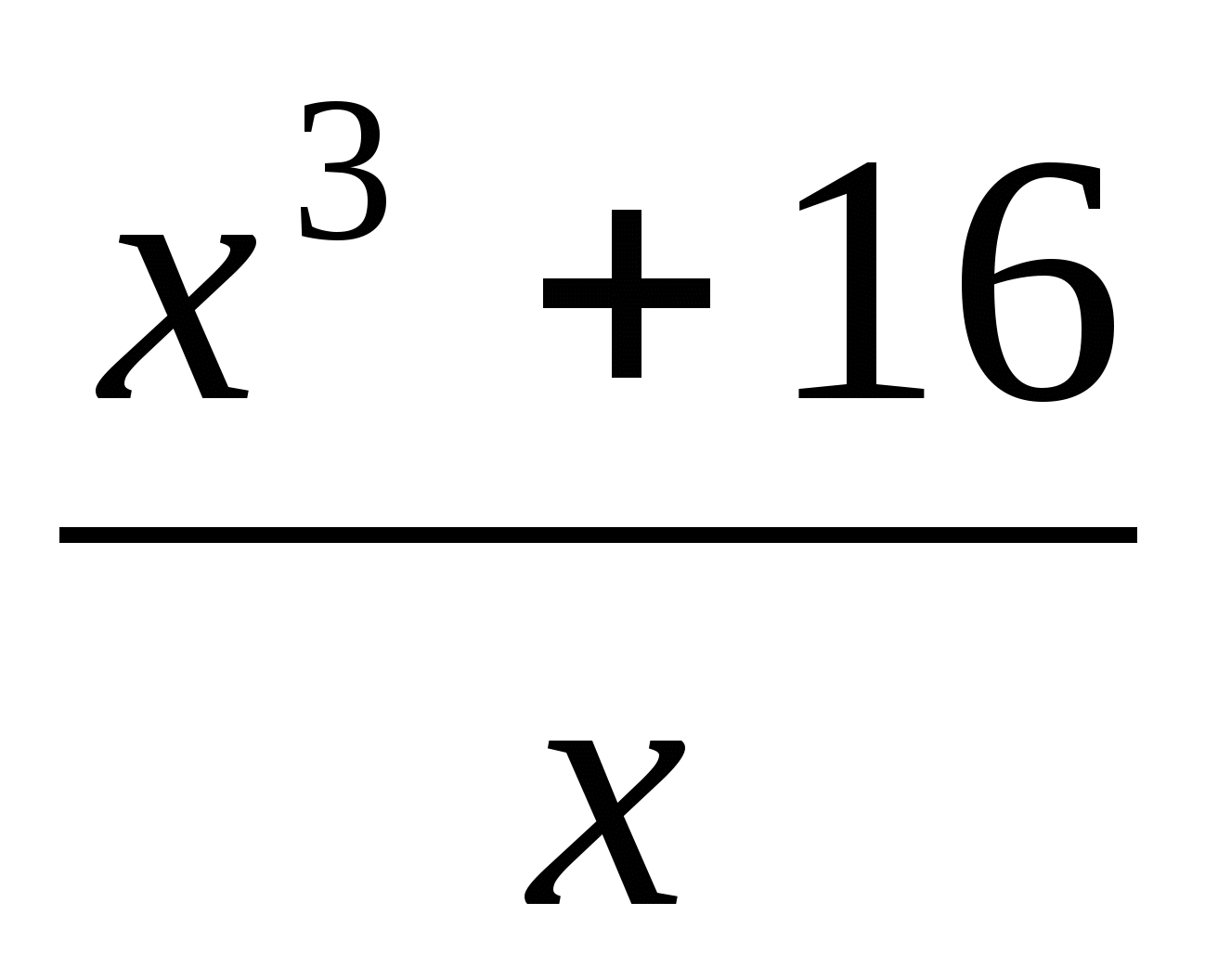. Ответ: х > 2.

3. Найти у´, если у = tg (3х - 1). Ответ: у´ = .

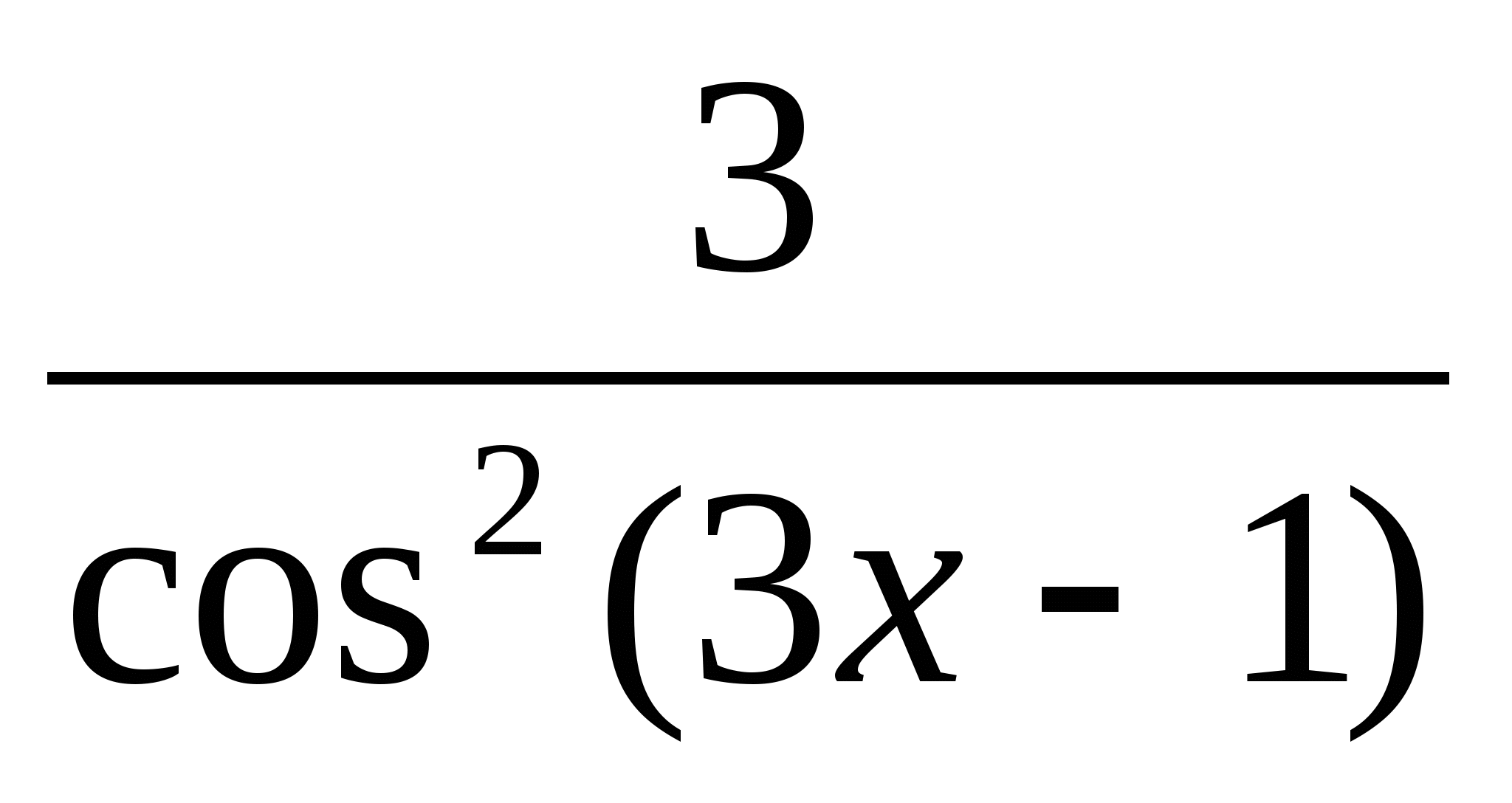4. Найти у´, если у = lg (sin x).

5. Составить уравнение касательной к графику функции у = 2х² - 2х + 1 в точке с абсциссой х₀ = 1. Ответ: у = 2х - 1.

6. Найти интервалы возрастания и убывания, точки экстремума функции f (x) = .

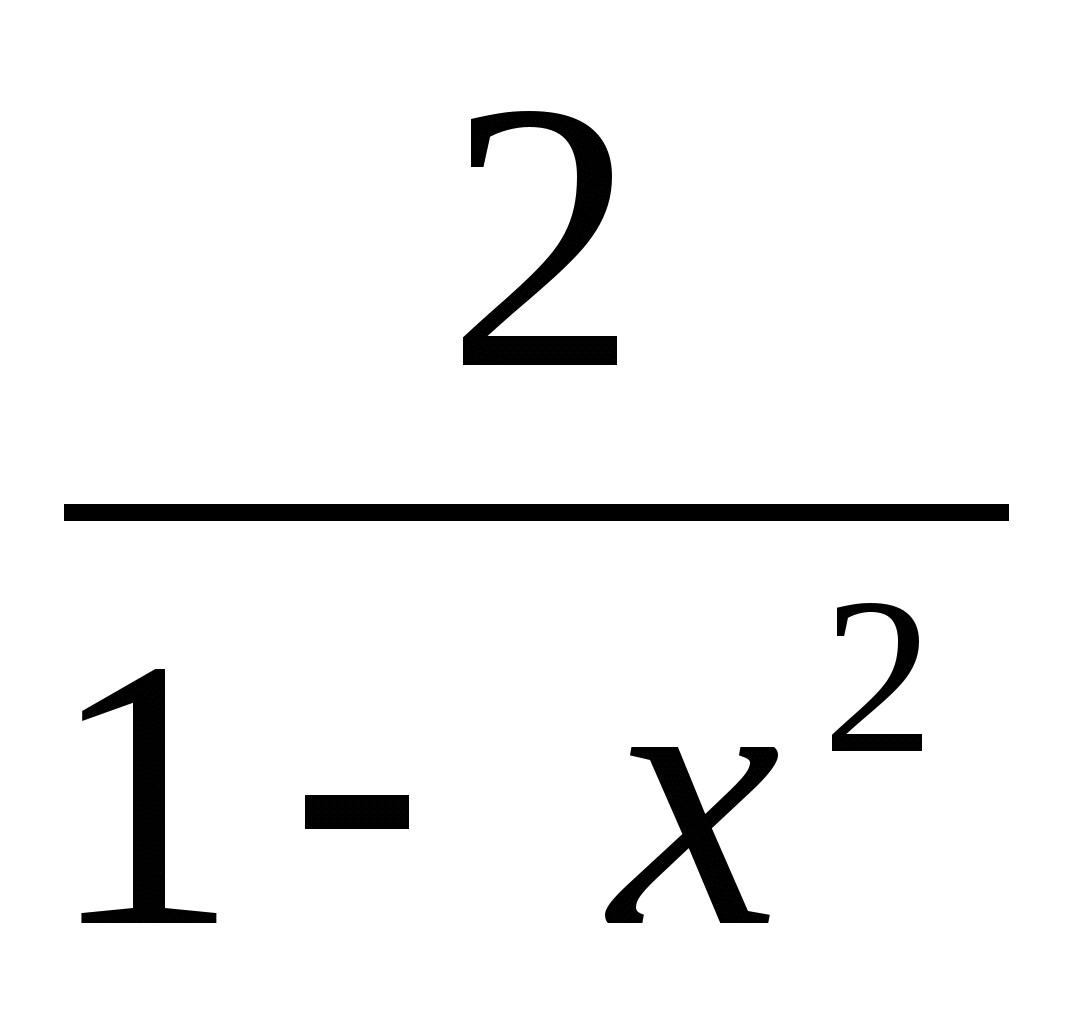Ответ: f (x) убывает, если х (- ; - 1) (- 1; 0]

f (x) возрастает, если х [0; 1) (1; + ).

0 - точка min.

в) Сильные учащиеся (IV, V группы) выполняют задания:

1. Найти у´, если у = 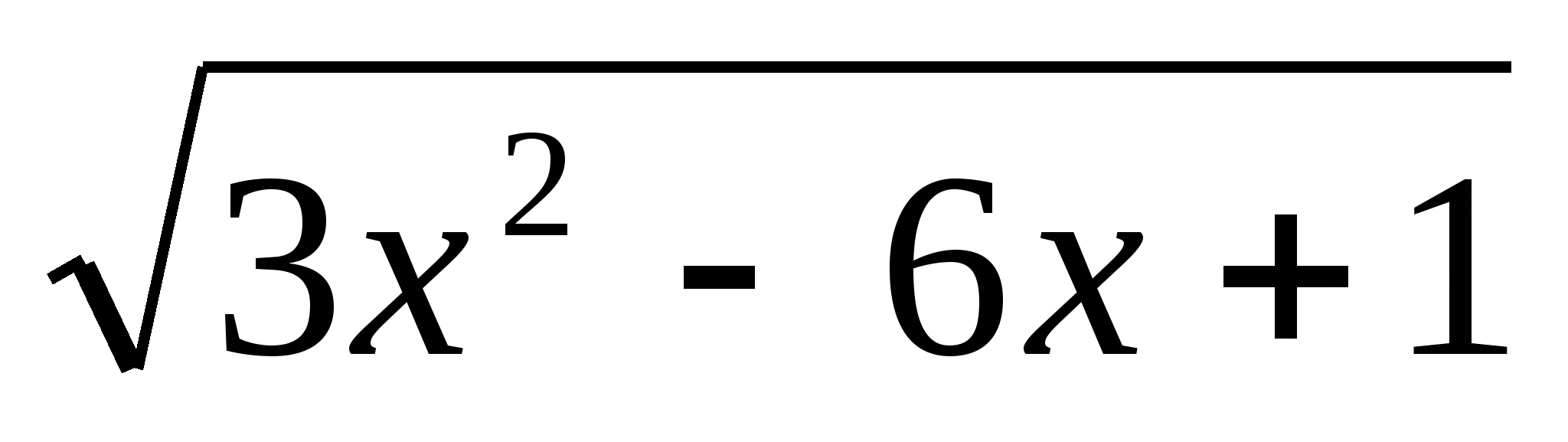. Ответ: у´= .

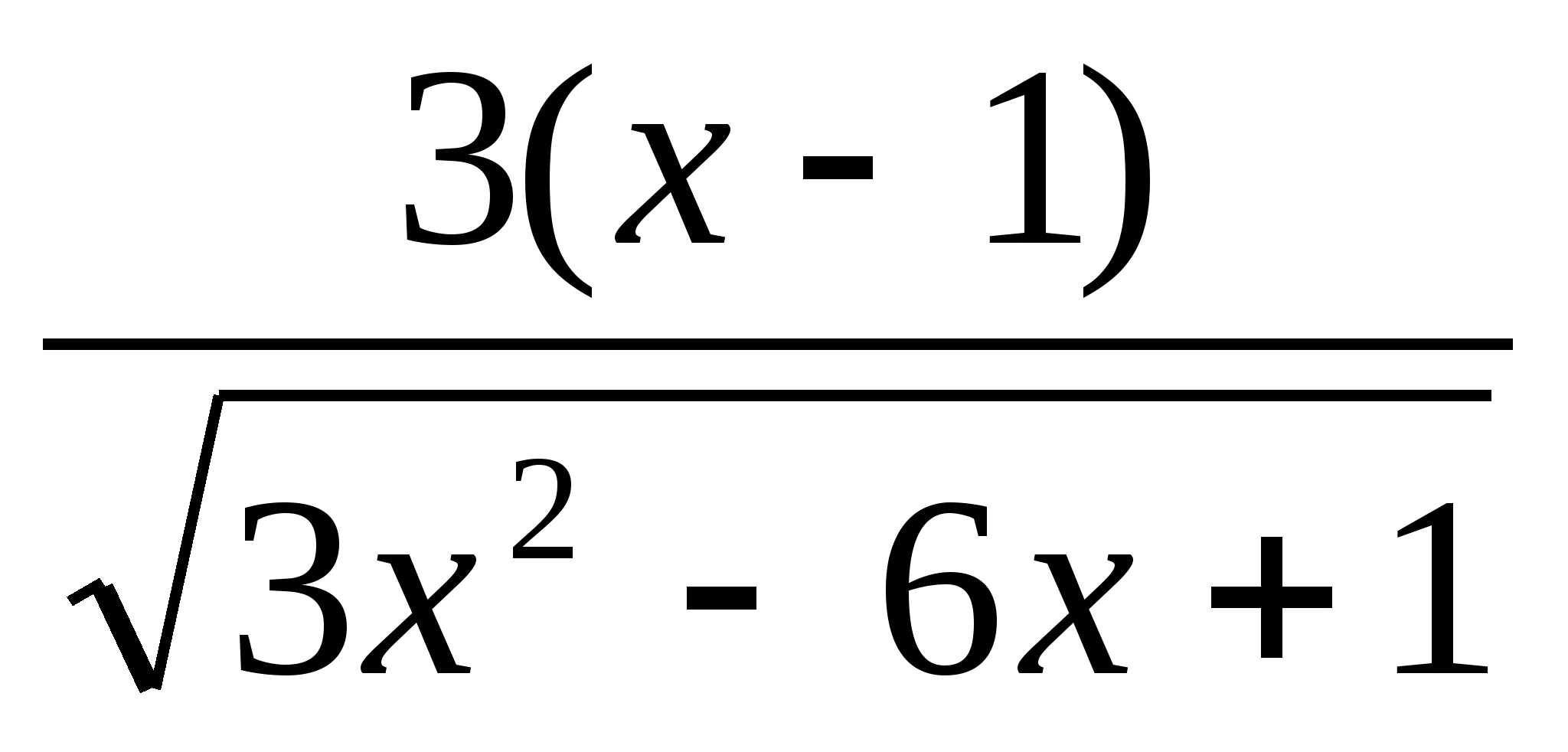2. Найти у´, если у = ctg⁴ х³. Ответ: у´= - .

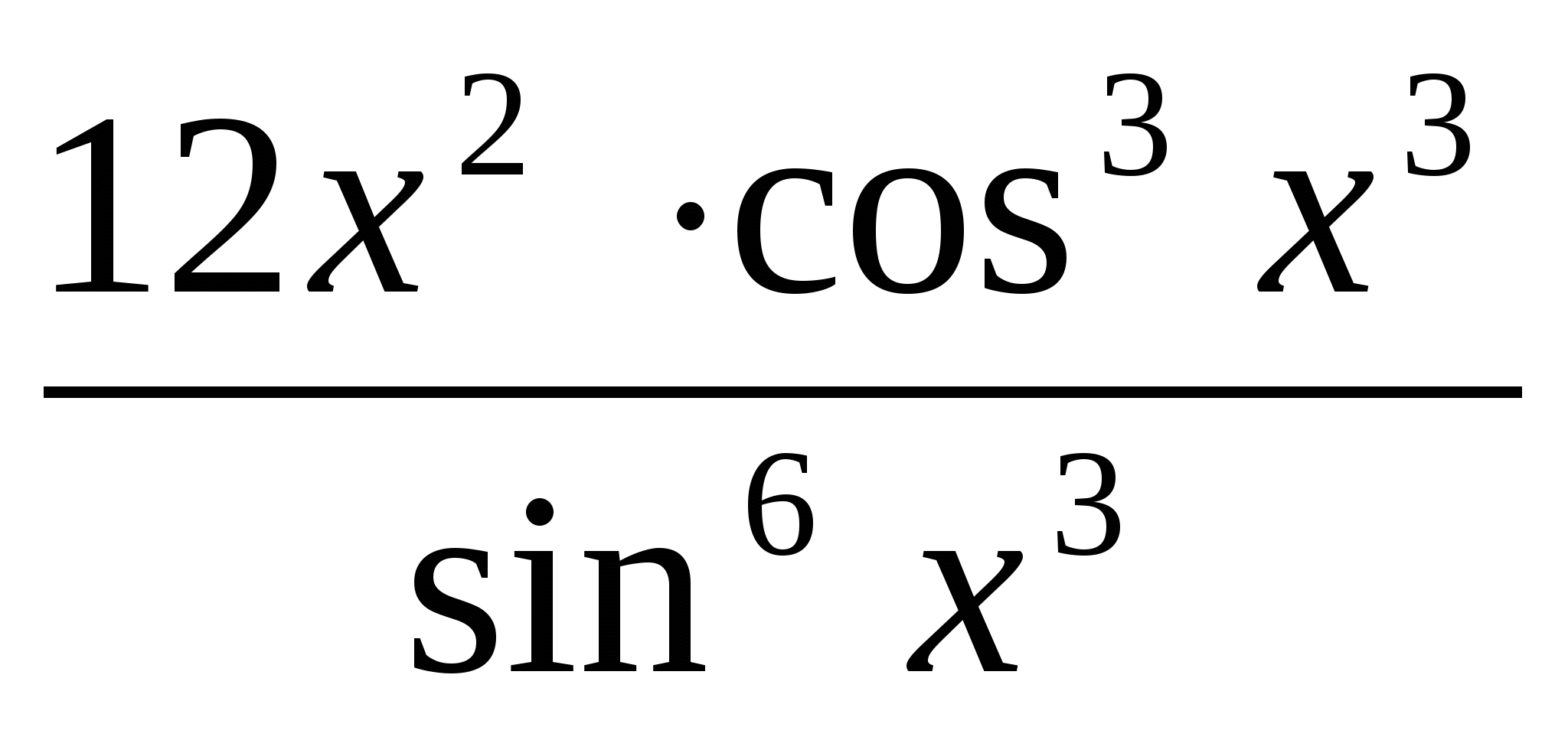3. Координата точки, движущейся вдоль оси Ох, изменяется по закону х (t) = - 4t² + 2t + 2. Найти, в какой момент времени скорость равна 1. Ответ: .

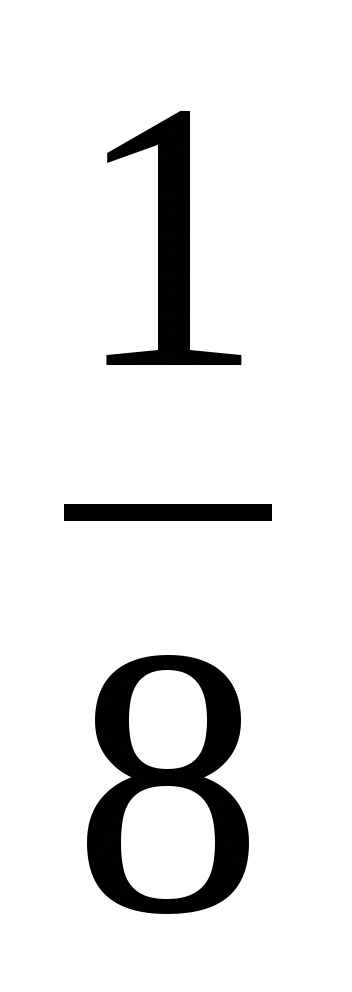4. Найти длину промежутка возрастания функции у = - 2х³ + 3х² + 36х + 1.

Ответ: Функция возрастает на интервале (-2; 3), длина которого равна 5.

5. При каком значении р функция у = - 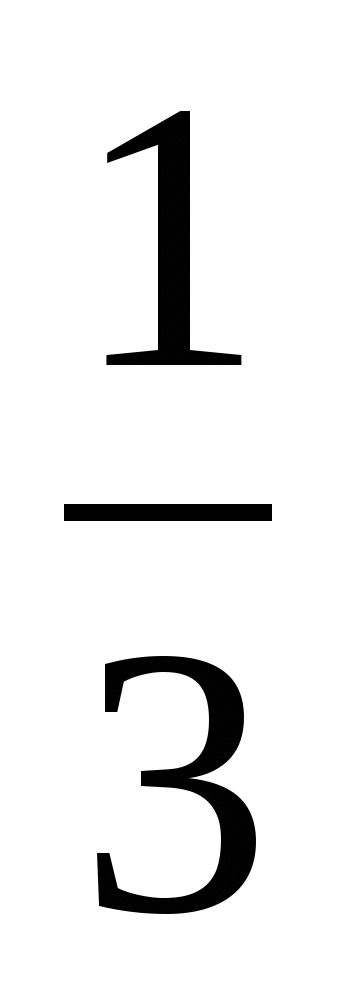х³ - 2х² + рх + 4х - 7 убывает на всей числовой прямой? Ответ: - 8.

Обсуждение задач происходит в группах, затем идет фронтальное обсуждение с учителем. Учащиеся работают в тетради с копиркой. По окончании работы сдают один лист учителю, другой оставляют для самопроверки.

Через проектор на экран проецируется таблица правильных ответов. Каждый учащийся выставляет себе баллы (за каждое верно выполненное задание - 1 балл).

г) В заключении семинара учащимся предлагается заработать дополнительную отметку, блеснув знаниями в блиц-турнире.

1. Какое значение принимает производная функции в точке А?

Ответы: у у = f(x)

а) f´ (x) > 0;

б) f´ (x) < 0;

в) f´ (x) = 0. А

0 1 х

2. Какое значение принимает производная функции в точке В?

Ответы: у

а) f´ (x) = 0; В

б) f´ (x) > 0;

в) f´ (x) < 0.

1 у = f(x)

0 х

3. Назовите промежуток убывания функции

Ответы: у

а) 0 < х < 2;

б) 0 х 2;

в) х > 2. у = f(x)

0

-1 1 2 3 4

4. Назовите промежуток возрастания функции

Ответы: у

а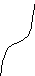) х < 0; у = f(x)

б) х > 0;

в) х - любое.

х

5. Назовите точки, в которых производная функции равна 0.

Ответы: у

а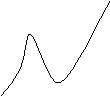) (; 1);

б) (0; 1);

в) (1; 0); 1

г) (0;0).

0 1 х

5. Подведение итогов.

В процессе работы на семинаре каждый ученик имеет возможность не только расширить и углубить свои знания, но и сравнивать уровень своих знаний с требованиями, предъявленными выпускнику школы.

Каждый ученик семинара получает 3 оценки: одну - за творческое выполнение домашнего задания, другую - за работу на семинаре, третью - за тест.

6. Домашнее задание:

Учащиеся получают индивидуальные разноуровневые карточки с заданиями.