- Учителю
- Научно исследовательская работа 'Оригометрия'
Научно исследовательская работа 'Оригометрия'
Введение
Для меня геометрия, и задачи по геометрии всегда вызывали и вызывают затруднения. Почему? Потому-то не всегда удается представить наглядно доказательство теоремы, увидеть и правильно построить чертеж. Доказательства некоторых теорем настолько сложные, что сначала приходилось вырезать модели фигур из бумаги, накладывать их друг на друга, сгибать, перегибать, чтобы понять доказательство теоремы и ли решение задачи. Японская пословица гласит: расскажи мне - я услышу, покажи мне - я запомню, дай мне сделать самому- я пойму!
Искусство оригами увлекло меня еще в раннем детстве. Я складывала фигурки из бумаги и обратила внимание, что искусство оригами сочетает в себе красивые формы и удивительно правильные линии. Оригами - это идеальный конструктор, который состоит из одной детали (листа), с помощью которой создается бесконечное разнообразие форм, складываются тысячи и тысячи разных фигурок. Мне стало интересно, насколько близко связано искусство оригами с математикой? Может быть, именно из-за этого мастера оригами говорят, что при складывании фигурок «голова работает руками» и очень успешно.
Оказалось, что есть наука, соединяющая две области: оригами и геометрию. Это оригаметрия. Оригаметрия - область очень молодая, и, наверное, поэтому мы пока не видели ни соответствующих программ, ни учебников, которые давали бы материал с помощью оригаметрии. Поэтому нашей задачей является изучение органического включения оригами в курс математики, в частности использование приемов сгибания бумаги для решения геометрической задачи.
Итак, возникла гипотеза, что применение техники оригами на уроках математики и геометрии помогает легче усвоить этот предмет.
Цель: доказать, что искусство оригами можно применять для доказательства теорем и для решения задач по геометрии.
Задачи:
1) Изучить литературу, подобрать задачи
2) Выполнить модели
3) Дать геометрическое обоснование оригамным действиям
Актуальность:
Тема оригами актуальна во все времена (им увлекались как в древности, так увлекаются и до сих пор), она интересна и занимательна. Кроме эстетического влияния, которое вносят в оригами японцы, оригами может помочь при выполнении геометрических построений.
Методы исследования: анализ литературы по теме, синтез, обобщение и аналогия, как организация практической деятельности по овладению оригамским методом решения задачи.
Практическая значимость исследовательской работы - овладение оригамским методом решения задач в процессе изучения геометрии.
Что же такое оригами?
Оригами - это японское искусство складывания бумаги, образовано от японского oru (складывать) и kami (бумага). Оригами - одно из самых доступных искусств, ведь для того, чтобы сложить фигурку требуется лишь листок бумаги. Родиной оригами является Япония. Объясняется это тем, что в этой стране процесс складывания удачно иллюстрировал некоторые мировоззренческие идеи философии Дзен. Немаловажным оказалось также сходство звучания японских слов "бумага" и "Бог" - "ками". Таким образом, у японцев возникала связь между религиозным ритуалом и складыванием фигурок из бумаги. В периоды Камакура (1185-1333) и Муромати (1333-1573) оригами выходит за пределы храмов и достигает императорского двора. Аристократия и придворные должны были обладать определенными навыками и в искусстве складывания. Записки, сложенные в форме бабочки, журавля, цветка или абстрактной геометрической фигуры, были символом дружбы или доброго пожелания для любимого человека. Различные знатные семьи использовали фигурки оригами как герб и печать. Сам термин оригами возник и закрепился только в 1880 году, когда данное искусство стало частью аристократического общества и вошло в число обязательных для японских семей. Япония, создавшая оригамную «азбуку», официально стала родиной оригами. Она задала некую классическую основу, от которой отталкивались остальные покорители искусства создания бумажных шедевров.
Не обошло стороной оригами и Россию, но сначала этот вид искусства был освоен детьми. Первым об оригами узнал юный наследник престола Николая II от учителя английского языка Чарльза Сиднея Гиббса, филолога из Кембриджа. Любовью к технике оригами отличался и великий русский писатель Лев Николаевич Толстой. В черновике к статье "Что такое искусство" он пишет: "Нынешней зимой одна мама научила меня делать из бумаги, складывая и выворачивая ее известным образом, петушков, которые, когда их дергаешь за хвост, махают крыльями. Выдумка эта от Японии. …как ни странно сказать, произведение такого петушка есть настоящее искусство
Новый поворот в истории оригами тесно связан со страшной трагедией, произошедшей 6 августа 1945 года, когда была сброшена атомная бомба на Хиросиму. Последствия чудовищного эксперимента были ужасны. Каждый, кто брался за оригами, знает историю Садако, девочки из Хиросимы, которая делала журавликов, веря, что это спасёт её от лучевой болезни. Кто-то сказал ей, что если она сделает 1000 журавликов, она поправится. Садако скоро поняла, что ей уже не станет лучше, она умрёт. И тогда она стала дарить журавликов другим больным. Каждый журавлик, которого делала Садако, был молитвой, молитвой о спасении человека. Девочка успела сложить 644 фигурки и умерла. Её подруги закончили остальных журавликов. Печальная история японской девочки подняла волну детской солидарности во всём мире. Япония стала получать миллионы посылок со всех континентов нашей планеты с бесценным грузом - бумажными журавликами. Так возникло движение «1000 журавликов» . Это движение вызвало интерес к японскому искусству оригами.
Появление авторских моделей и начало развития оригами, как направления современного искусства, связывают с именем знаменитого японского мастера Акиры Йошизавы. Во второй половине двадцатого века он уже активно пользуется придуманной им системой записи процесса складывания и извлекает из хорошо известных базовых форм множество новых моделей.
Министерство иностранных дел Японии отправляет Акиру Йошизаву в Европу, возложив на него почетную миссию: посредством оригами добиваться мира и дружбы со всеми странами.
Мощный толчок развитию отечественного оригами дает создание в 1989 и 1991 гг. двух общественных организаций - Московского и Петербургского центров оригами. Число отечественных изобретений, зарегистрированных в базе данных Петербургского центра оригами в 1998 г. превышает тысячу. Многие из этих работ вызывают должное восхищение у зарубежных оригамистов. В настоящее время организуются и олимпиады по оригами, что еще раз подтверждает значимость занятия оригами.
Многие предметы вокруг нас имеют форму, похожую на геометрические фигуры. Альбомный лист имеет форму прямоугольника. Если поставить круглый стакан на лист бумаги и обвести его карандашом, получится линия, изображающая окружность. Кольцо, обруч напоминают своей формой окружность, а арена цирка, дно стакана или тарелка имеют форму круга. Апельсин, футбольный мяч, арбуз похожи на шар. Шестигранный карандаш, египетские пирамиды - это тоже геометрические фигуры.
Геометрия - это наука о свойствах геометрических фигур: треугольника квадрата, круга, пирамиды сферы и др.
Слово «геометрия» греческое, в переводе на русский язык означает «землемерие». Принято считать, что геометрия зародилась в Древней Греции. Но греки переняли у египтян основы землемерия и превратили его в научную дисциплину путём установления общих закономерностей. Главным трудом по геометрии являются «Начала» древнегреческого учёного Евклида, составленные около 300 лет до н.э. Этот труд длительное время считался образцовым.
В 1877 году немецкий математик Феликс Клейн в своей «Эрлангерской программе» предложил классификацию различных разделов геометрии, которая используется и в наши дни: евклидова геометрия, проективная, аффинная, начертательная, многомерная, риманова, неевклидова геометрии, геометрия многообразий, топология.
Евклидова геометрия изучает простейшие геометрические формы: точки, прямые, отрезки, многоугольники, шары, пирамиды и др. Именно этот раздел геометрии изучается в школе.
Евклидова геометрия состоит из двух частей: планиметрии и стереометрии.
Планиметрия - это раздел геометрии, в котором изучаются геометрические фигуры на плоскости.
Стереометрия - это раздел геометрии, в котором изучаются фигуры в пространстве.
В наше время в Японии, США и других развитых странах обучение геометрии при помощи оригами практикуется во многих школах.
Если в прошлом математика применялась в довольно ограниченном числе областей жизни человека, будучи, следовательно, необходимой сравнительно небольшому числу специалистов, то в современную эпоху математика проникла во все те области, в которых практикуется рациональное мышление, и этот процесс, находящийся в постоянном развитии, требует соответствующей математической подготовки.
Простые базовые формы
Треугольник
Книга
Дверь

Воздушный змей
Средние базовые формы
Блин
Рыба
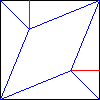
Двойной треугольник
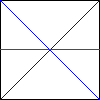
Двойной квадрат
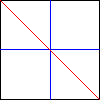
Видя эти формы мы понимаем, что на занятиях по математике при помощи оригами можно повторить следующие понятия:
- горизонтальные, вертикальные, наклонные линии;
- сложи квадрат разными способами, покажи смежные стороны, диагональ;
- квадраты;
- все виды треугольников.
В ходе изучения геометрии с использованием оригами знакомимся с основными геометрическими фигурами (треугольник, прямоугольник, квадрат, ромб, четырехугольник), понятиями (сторона угол, вершина угла, диагональ, центр фигуры), их свойствами и учимся основам техники оригами.
Работа по схемам, процесс складывания плоскостных фигур направлены на развитие восприятия, которое связано с различными операциями мышления. Складывая их в различных комбинациях, можно получить многогранники. Здесь особое место занимает метод решения задач на построение без помощи циркуля и линейки. Особая ценность этого метода в том, что он позволяет построить правильные многоугольники, построение которых с помощью циркуля и линейки затруднительно, а в некоторых случаях невозможно.
Виды и техники оригами
Простое оригами - стиль оригами, придуманный британским оригамистом Джоном Смитом, и который ограничен использованием только складок горой и долиной. Целью оригами является облегчение занятий неопытным оригамистам, а также людям с ограниченными двигательными навыками. Данное выше ограничение означает невозможность многих (но не всех) сложных приёмов, привычных для обычного оригами, что вынуждает к разработке новых методов, дающих сходные эффекты.
Модульное оригами
Одной из популярных разновидностей оригами является модульное оригами, в котором целая фигура собирается из многих одинаковых частей (модулей). Каждый модуль складывается по правилам классического оригами из одного листа бумаги, а затем модули соединяются путём вкладывания их друг в друга, появляющаяся при этом сила трения не даёт конструкции распасться. Одним из наиболее часто встречающихся объектов модульного оригами является кусудама, объёмное тело шарообразной формы. Традиционно их подвешивали над постелью больного, действительно поместив внутрь лечебные травы (КУСУДАМА и означает в переводе "лечебная трава"). Их не нюхали и не заваривали, но, странное дело, со временем больному становилось легче. Самое удивительное, что волшебные КУСУДАМЫ нередко помогают преодолеть лёгкий недуг и без всяких трав.
Складывание по развёртке
Развёртка (англ. creasepattern; паттерн складок) - один из видов диаграмм оригами, представляющий собой чертёж, на котором изображены все складки готовой модели. Складывание по развёртке сложнее складывания по традиционной схеме, однако, данный метод даёт не просто информацию, как сложить модель, но и как она была придумана - дело в том, что развёртки используются при разработке новых моделей оригами. Последнее также делает очевидным факт отсутствия для некоторых моделей иных диаграмм, кроме развёртки.
Мокрое складывание - техника складывания, разработанная Акирой Ёсидзавой и использующая смоченную водой бумагу для придания фигуркам плавности линий, выразительности, а также жесткости. Особенно актуален данный метод для таких негеометричных объектов, как фигурки животных и цветов - в этом случае они выглядят намного естественней и ближе к оригиналу.
Не всякая бумага подходит для мокрого складывания, а лишь та, в которую при производстве добавляют водорастворимый клей для скрепления волокон. Как правило, данным свойством обладают плотные сорта бумаги.
Киригами - вид оригами, в котором допускается использование ножниц и разрезание бумаги в процессе изготовления модели. Это основное отличие киригами от других техник складывания бумаги, что подчёркнуто в названии: (киру) - резать, (ками) - бумага.
Большинство людей помнит, как в детстве делали бумажные снежинки. Да и взрослые с восхищением и удивлением разворачивают бумажные снежинки, к тому же почти невозможно сделать один и тоже образец дважды. В дополнение к снежинкам можно вырезать различные цветы, паутинки и другие элементы декоративного оформления. Так вот эти бумажные Снежинки и декорации и есть первые шаги в изучении техники Киригами.
Чаще всего люди воспринимают оригами просто как способ изготовления бумажных игрушек и украшений интерьера, и мало кто задумывается о том, что это древнее искусство имеет тесную связь с математикой. Развернув фигурку оригами и посмотрев на складки, я увидел множество многоугольников, соединенных друг с другом. В сложенном виде оригами представляет собой многогранник, фигуру с множеством плоских поверхностей. Складывание самой простой фигуры оригами включает в себя решение простейших геометрических задач на построение, таких, как построение перпендикуляра к данной прямой, построение биссектрисы угла и т.д. Различные построения и фигуры оригами складываются, как правило, из квадратного листа бумаги. Таким образом, когда мы производим простейшее действие с листом бумаги, например, складываем его по вертикали или диагонали, мы уже решаем задачи на построение : строим перпендикуляр к прямой или биссектрису угла.
Возможности перегибания листа бумаги велики, что обеспечивает решение большого разнообразия задач.
В конце XX века возник новый термин «оригаметрия», обозначающий область геометрии, в которой задачи решаются только методом складывания.
Оригами обладает мощным потенциалом в решении планиметрических задач на построение. Например
1) построение биссектрисы угла;
2) построение высоты треугольника;
3) построение медианы.
При решении задач с помощью методов оригами роль прямых играют края листа и линии сгибов, образующиеся при его перегибании, а роль точек - вершины углов листа и точки пересечения линий сгибов друг с другом или с краями листов.
Любая оригамская задача состоит:
1. Из постановки задачи.
2. Из оригамского решения, проверки или способа построения.
3. Из математического обоснования, то есть доказательства того, что в результате действительно получается фигура с требуемыми свойствами.
Для построения теории оригаметрии используется система аксиом. Их предложил живущий в Италии японский математик Хумиани Хузита.Таких аксиом, с его точки зрения, всего шесть.
Аксиома 1. Существует единственный сгиб, проходящий через две данных точки.
Аксиома 2. Существует единственный сгиб, совмещающий две данные точки.
Аксиома 3. Существует единственный сгиб, совмещающий две данные прямые.
Аксиома 4. Существует единственный сгиб, проходящий через данную точку и перпендикулярный данной прямой.
Аксиома 5. Существует единственный сгиб, проходящий через данную точку и помещающий другую данную точку на данную прямую.
Аксиома 6. Существует единственный сгиб, помещающий каждую из двух данных точек на одну из двух данных пересекающихся прямых.
Доказательство теорем с помощью оригами.
Теорема 1.Суммауглов любого треугольника равна 180 градусов.
Доказательство. Возьмем лист бумаги, имеющий форму произвольного треугольника.
1) Проведем сгиб через одну из вершин треугольника, перпендикулярно противоположной стороне (высоту треугольника).
2) Совместим вершины треугольника с точкой у основания высоты треугольника.
3)Получаем, что углы 1, 2 и 3 треугольника совпали при наложении с развернутым углом, следовательно, сумма углов равна 180 градусов.
Теорема 2. Накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей, равны.
Доказательство. 1) Возьмем лист бумаги с двумя параллельными сторонами и секущей АВ. Сравним накрест лежащие углы- углы 1 и 2.
2) Совместим вершины накрест лежащих углов- точки А и В.
3)Углы 1 и 2 совпали при наложении, следовательно, угол 1 равен углу 2. Значит, накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей, равны.
Задача: Прямая, проходящая через середину биссектрисы AD треугольника АВС и перпендикулярная AD, пересекает сторону АС в точке М.Доказать, что MD //AB.
Решение: Возьмем лист бумаги, имеющий форму производного треугольника. Проведем биссектрису AD, согнув лист так, чтобы сторона АС совместилась со стороной АВ. Наметим середину АD, совместив точки А и D. Проведем ОМ, перпендикулярнуюAD. Согнем лист по линии MD.Для доказательства параллельности MD и АВ сравним углы 1 и 3, для этого согнем лист по AD и совместим точки А и D. Углы 1 и3 совпали, а они накрест лежащие ,следовательно, MD // AB.
Заключение.
Оригами и математика, словно две сестры, которые не терпят неточности и поспешности. Само оригами дает полет фантазии, а математика эту фантазию облачает в платье науки.
Японское искусство оригами очень широко вошло в нашу российскую жизнь и стало неотъемлемой частью для интеллектуального и познавательного развития. По результатам анкетирования в нашей школе как учителя, так и ученики считают, что оригами способствует в первую очередь развитию математических качеств (наблюдательность, внимание и произвольность, логическое и пространственное мышление, точность и аккуратность) человека. Это умение необходимо как на основных уроках - математика (геометрия, стереометрия), ИЗО, труд, так и на дополнительных элективных занятиях, кружках.(Приложение 4.)
В ходе изучения данной темы мы смогли прикоснуться к тайнам оригами, понять смысл математических принципов в бумажной пластике. Выполняя геометрические фигуры в технике оригами, учащиеся знакомятся с новыми геометрическими понятиями, основными определениями, и наглядно изучают закономерности поведения двухмерной плоскости в трехмерном пространстве. Значит оригами , действительно, помогает изучать математику.
Оригами - это семейный, коллективный досуг, сближающий, улучшающий психологический фон семьи и коллектива. Каждая фигура оригами - это своя история, своя легенда и множество вариантов применения в жизни.