Решение задач по геометрии ГИА 11 класс 2 часть

Задача №11.

Основанием прямой треугольной призмы служит прямоугольный треугольник с гипотенузой 13 см и катетом 5 см. Высота призмы равна радиусу окружности, вписанной в основание призмы. Найти объем призмы.

Решение.

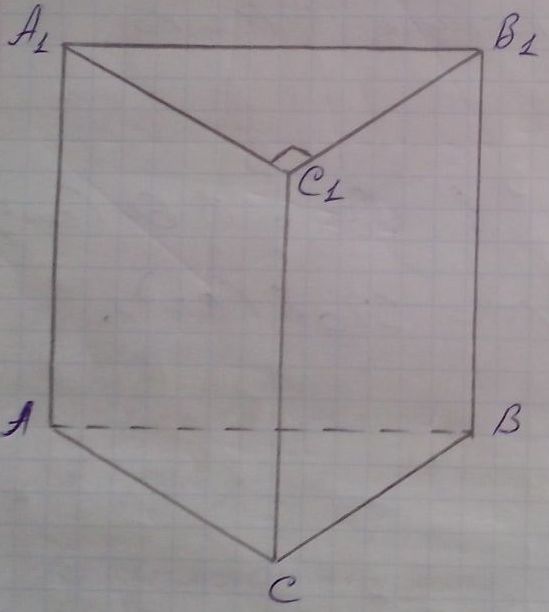
Пусть - прямая треугольная призма. ∆АВС - прямоугольный треугольник, ее основание, АСВ = 90º. По условию АВ = 13 см, АС = 5 см. , - высота призмы. По условию = r, где r - радиус окружности, вписанной в основание призмы.

Из ∆АВС, (АСВ = 90º), используя теорему Пифагора СВ = , СВ = . Радиус окружности, вписанной в ∆АВС , где - площадь треугольника, р - полупериметр треугольника, р = = , = , тогда ,

=2см.

Объем призмы V = , где - площадь основания призмы, = - высота призмы. V = 30 · 2 = 60 (см²).

Ответ: 60 см².

Задача №12.

Основанием прямой треугольной призмы служит прямоугольный треугольник с гипотенузой 17 см и катетом 8 см. Высота призмы равна радиусу окружности, описанной около основания призмы. Найти объем призмы.

Решение.

Пусть - прямая треугольная призма. ∆АВС - прямоугольный треугольник, ее основание, АСВ = 90º. По условию АВ = 17 см, АС = 8 см. , - высота призмы. По условию = R, где R - радиус окружности, описанной около основания призмы.

Построим точку М - середину гипотенузы АВ - это центр окружности, описанной около ∆АВС, R = МА = МВ =, R =

Из ∆АВС, (АСВ = 90º), используя теорему Пифагора СВ = , СВ = .

Объем призмы V = , где - площадь основания призмы, = - высота призмы. = V = 60 ·

Ответ: 510 см².

Задача 13. В правильной треугольной пирамиде радиус окружности, вписанной в основание, равен см. Апофема пирамиды равна 2см. Найдите объем пирамиды.

Решение.

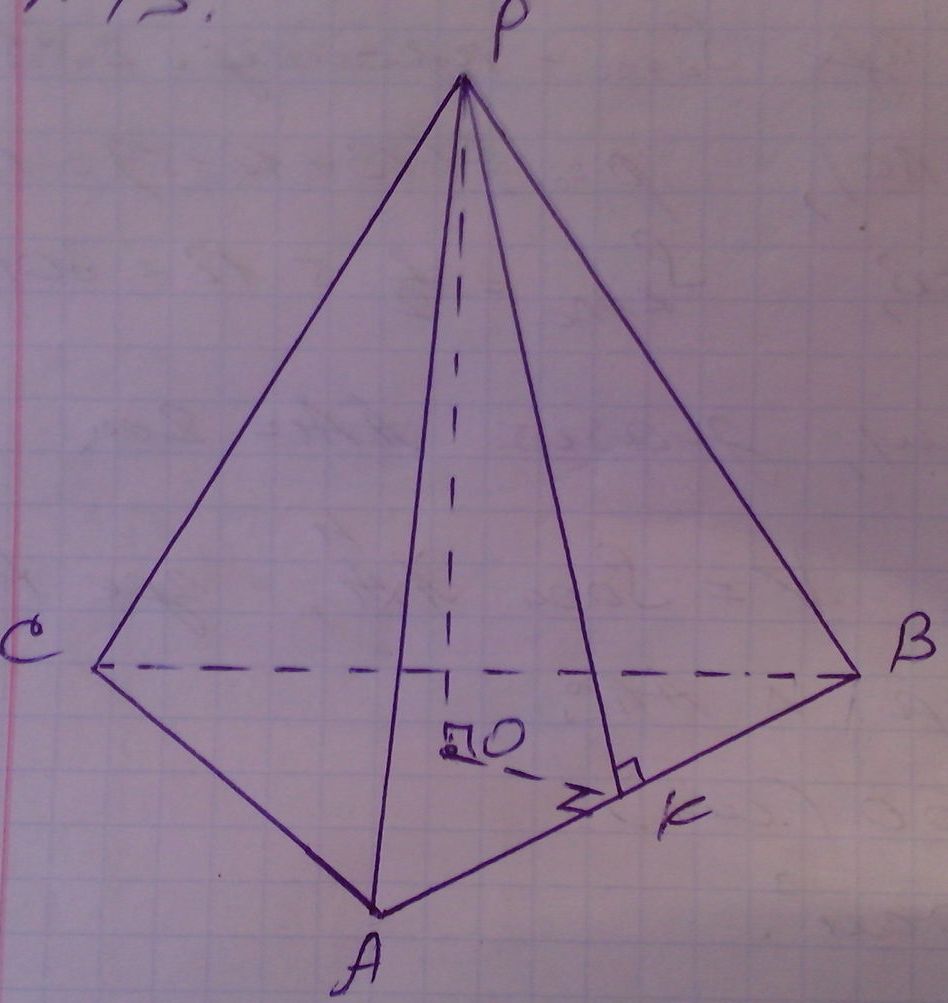
Пусть дана правильная треугольная пирамида РАВС, значит ее основание правильный треугольник АВС. Высота РО проходит через его центр, точку О. Точка О - центр вписанной окружности. Проведем апофему РКАВ, по условию РК = 2см. РО (АВС), ОК - проекция РК на плоскость основания. По теореме о трех перпендикулярах АВ ОК, значит ОК - радиус окружности, вписанной в ∆АВС, ОК = r = см по условию задачи. Так как ∆АВС - правильный, АВ = ВС = СА, то 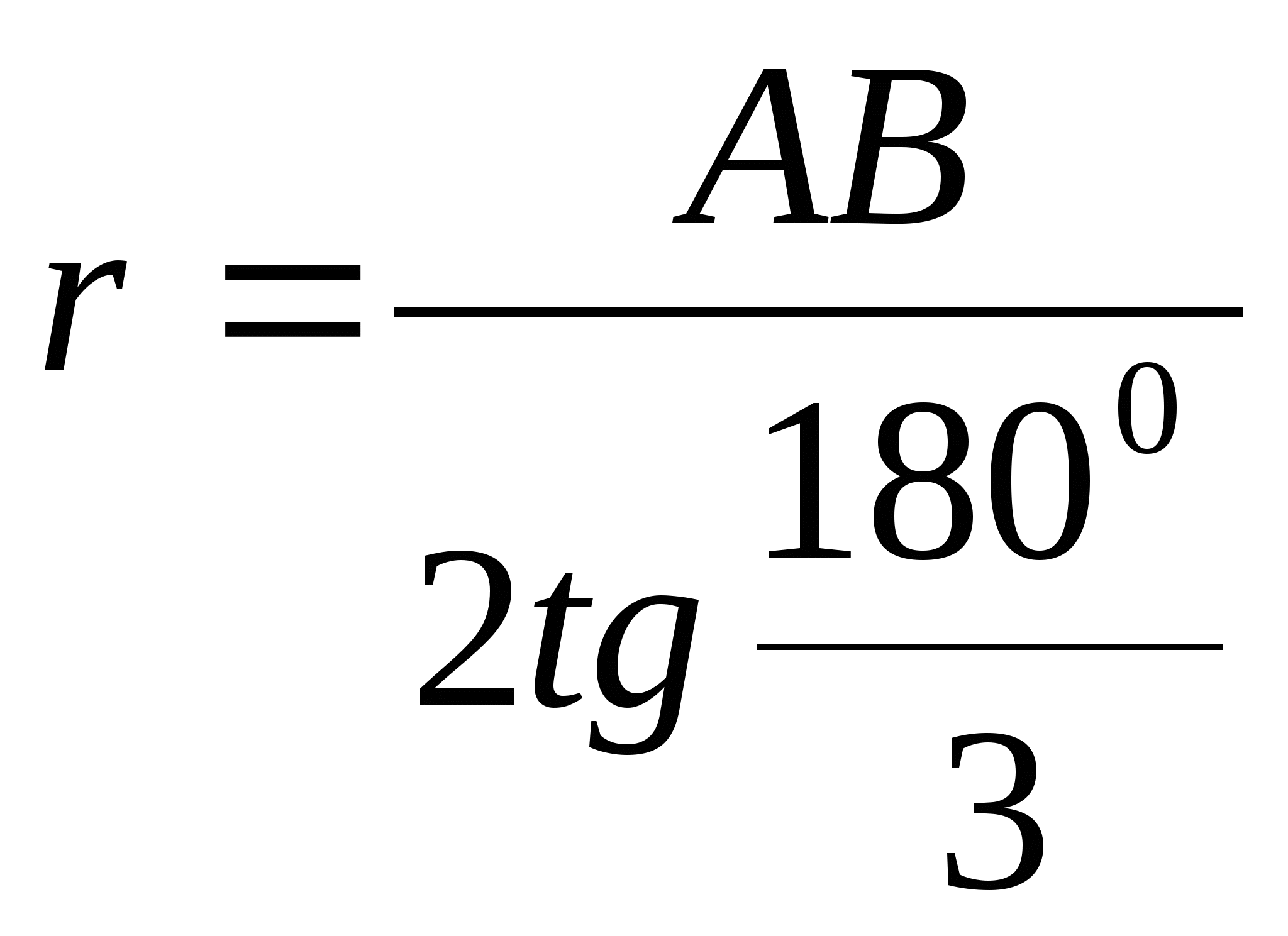, АВ = 2r∙tg60º, AB = 2·=6 (см).

Из ∆РОК (РОК = 90º), используя теорему Пифагора РО = , РО = = 5 (см).

Объем пирамиды V=, где - площадь основания, т.е. площадь правильного треугольника АВС, Н=РО=5см. , . V = .

Ответ: .

Задача 14. В правильной треугольной пирамиде боковое ребро равно см. Найдите объем пирамиды, если радиус окружности, описанной около основания, равен см.

Решение.

А

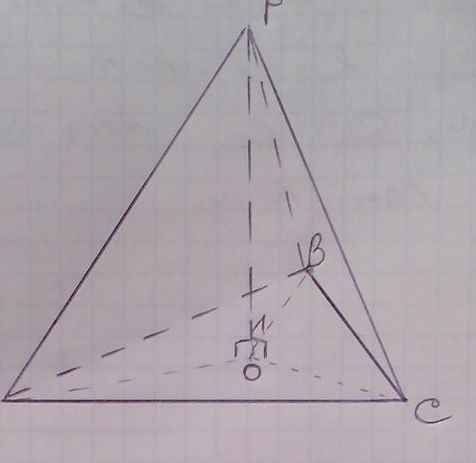
Пусть дана правильная треугольная пирамида РАВС, значит ее основание правильный треугольник АВС. Высота РО проходит через его центр, точку О. Точка О - центр описанной окружности, ОА = ОВ = ОС = R, где R - радиус описанной окружности. По условию задачи R = см. Боковые ребра правильной пирамиды равны, РА = РВ = РС и по условию задачи равны см.

Так как в основании пирамиды лежит правильный треугольник, то R = 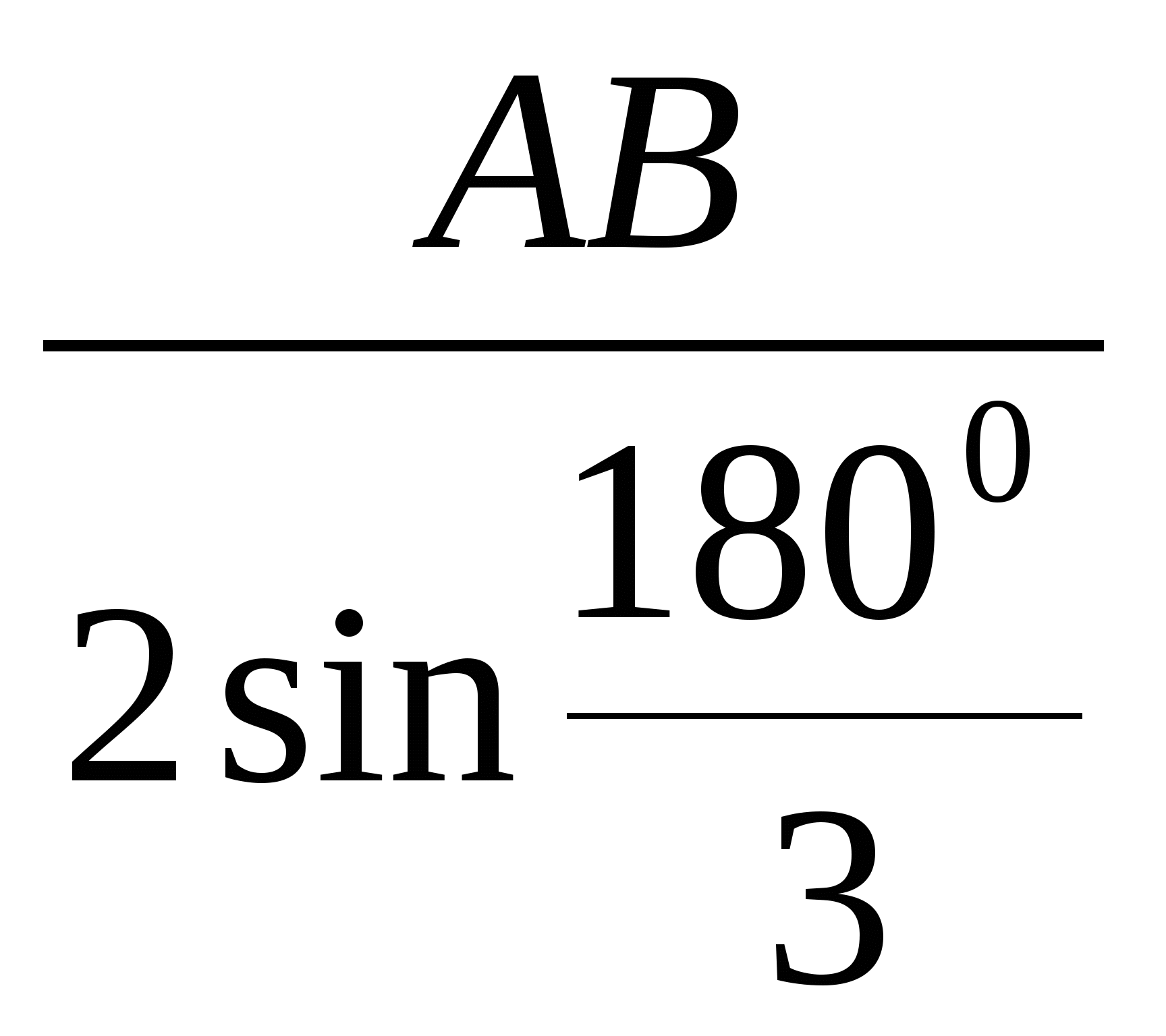= , откуда АВ = , АВ = ∙=6 (см).

Объем пирамиды V=, где - площадь основания, т.е. площадь правильного треугольника АВС, Н - высота, Н = РО.

, .

Из ∆РОА, (РОА = 90º), используя теорему Пифагора РО = , РО = = 5 (см).

V = .

Ответ: .

Задача 15. Основание прямой призмы - ромб с диагоналями 10 см и 24 см. Меньшая диагональ призмы равна 26см. Вычислите площадь полной поверхности призмы.

Решение.

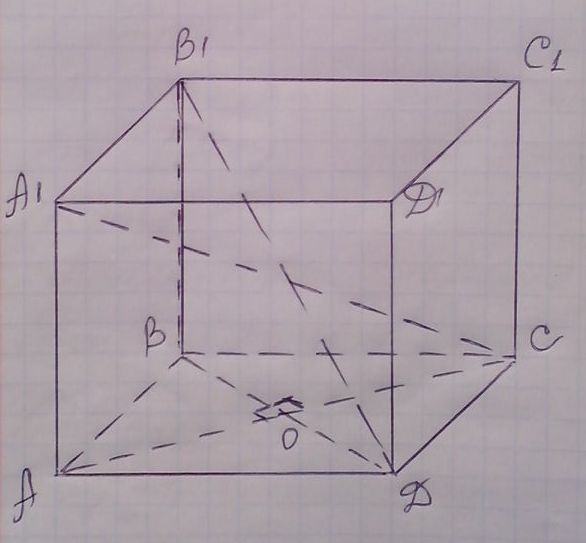
Пусть - прямая призма, ромб АВСД - ее основание. Точка О - точка пересечение диагоналей ромба, А - острый, АС - большая диагональ ромба, ВД - меньшая диагональ ромба, АС > ВД. , АС - проекция на плоскость основания, , ВД - проекция на плоскость основания. Так как АС > ВД, то > по свойству наклонных и их проекций, значит - меньшая диагональ призмы. По условию задачи АС = 24 см, ВД = 10 см, ВД = 26 см.

Площадь полной поверхности призмы , где площадь боковой поверхности призмы, площадь основания.

, . , где Р - периметр основания призмы, Н - высота, Н=ВВ. Рассмотрим ромб АВСД, по свойству диагоналей ромба АО = , АО = 12см, ВО = , ВО = 5 см. Из ∆АОВ, (АОВ = 90º), используя теорему Пифагора АВ = , АВ = = 13 (см). Периметр ромба Р = 4·13=52 (см).

Из ∆ВВД, (ВВД=90º), используя теорему Пифагора ВВ=, ВВ=. Тогда , .

Ответ: .

Задача 16. Основание прямой призмы - ромб с диагоналями 16 см и 30 см. Большая диагональ призмы равна 50 см. Вычислите площадь полной поверхности призмы.

Решение.

Пусть - прямая призма, ромб АВСД - ее основание. Точка О - точка пересечение диагоналей ромба, А - острый, АС - большая диагональ ромба, ВД - меньшая диагональ ромба, АС > ВД. , АС - проекция на плоскость основания, , ВД - проекция на плоскость основания. Так как АС > ВД, то > по свойству наклонных и их проекций, значит - большая диагональ призмы. По условию задачи АС = 30 см, ВД = 16 см, АС = 50 см.

Площадь полной поверхности призмы , где площадь боковой поверхности призмы, площадь основания.

, . , где Р - периметр основания призмы, Н - высота, Н=АА. Рассмотрим ромб АВСД, по свойству диагоналей ромба АО = , АО = 15 см, ВО = , ВО = 8 см. Из ∆АОВ, (АОВ = 90º), используя теорему Пифагора АВ = , АВ = = 17 (см). Периметр ромба Р = 4·17 = 68 (см).

Из ∆ААС, (ААс=90º), используя теорему Пифагора АА=, АА=. Тогда , .

Ответ: .

Задача 17. Полная поверхность прямоугольного параллелепипеда, основанием которого служит квадрат, равна 264см². Найдите сторону основания параллелепипеда, если его высота равна 8 см.

Решение.

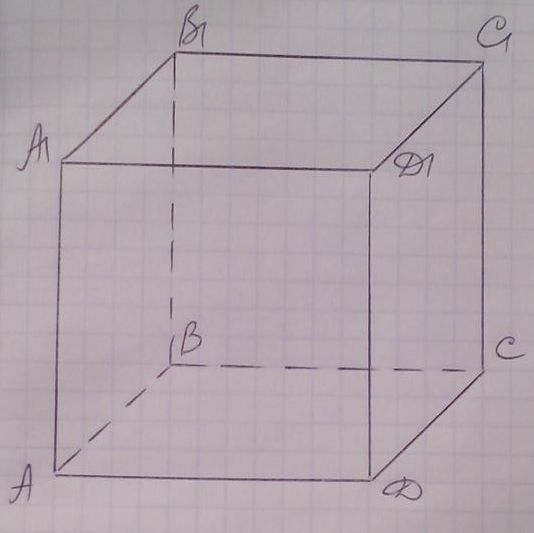
Пусть - прямоугольный параллелепипед, боковые ребра перпендикулярны основанию и равны, АА Основание квадрат АВСД. У параллелепипеда все грани - равные прямоугольники, поэтому площадь полной поверхности параллелепипеда , где - площадь боковой поверхности, - площадь основания.

По условию 264 см², высота АА=8 см. = 4АВ∙ АА, =АВ², тогда 4АВ∙ АА + 2 АВ² = 4АВ·8 + 2АВ² = 264 см². Получим уравнение 2АВ² + 32АВ - 264 = 0, АВ² + 16АВ - 132 = 0, АВ = (см) или АВ = (см), так как по условию задачи АВ>0, то АВ = 6 см.

Ответ: 6 см.

Задача №18.

В прямоугольном параллелепипеде его измерения относятся как 1:2:3. Полная поверхность параллелепипеда равна 352 см². Найдите его измерения.

Решение.

Пусть - прямоугольный параллелепипед, боковые ребра перпендикулярны основанию и равны, АА Основание прямоугольник АВСД. У параллелепипеда противоположные грани - равные прямоугольники, поэтому площадь полной поверхности параллелепипеда , где - площадь боковой поверхности, - площадь основания.

По условию измерения прямоугольного параллелепипеда АД:ДС:АА=1:2:3. Пусть х - коэффициент пропорциональности, тогда АД = 1х, ДС = 2х, АА= 3х.

, , по условию Тогда 22х² = 352, х=4 (х>0). Тогда АД = 4 см, ДС=2·4=8 см, АА=3·4=12 см.

Ответ: 4см, 8см, 12см.

Задача №19.

Длина линии пересечения сферы и плоскости равна 10πсм. Радиус сферы равен 13 см. Найдите расстояние от центра сферы до плоскости сечения.

Решение.

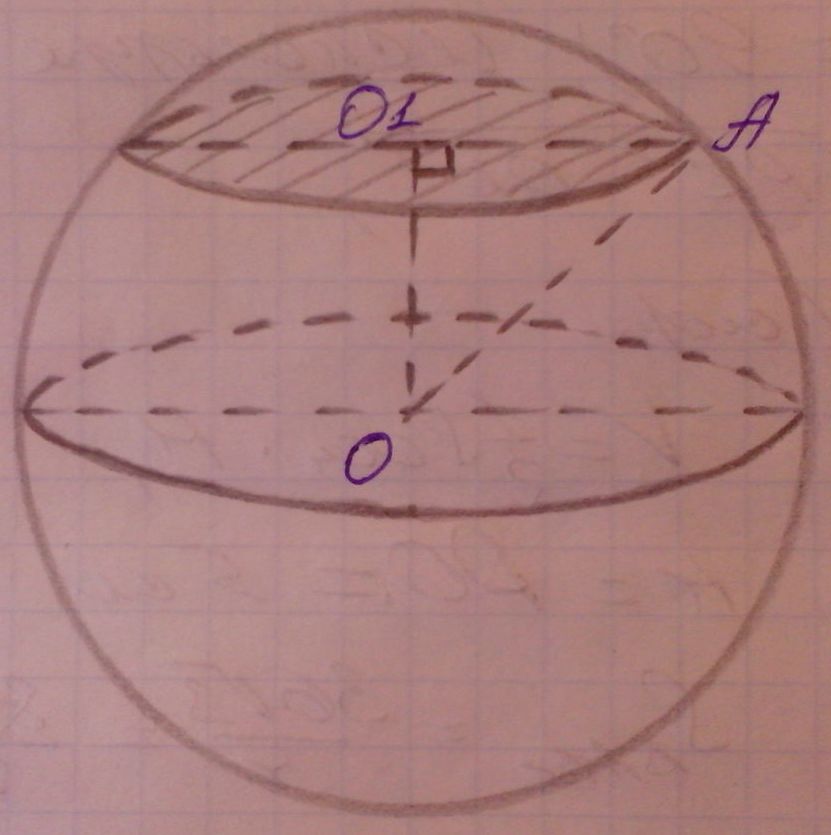
Пусть дана сфера с центром в точке О. Сечение сферы плоскостью - окружность с центром в точке О. Так как центр О этой окружности есть основание опущенного перпендикуляра ОО на плоскость сечения, то ОО - расстояние от центра сферы до заданной плоскости сечения.

По условию длина окружности С = 2πОА, где ОА - радиус окружности с центром в О, 2πОА = 10π, ОА = 5 см.

Проведем радиус сферы ОА = R, где А - точка, принадлежащая окружности сечения. По условию ОА = 13 см.

Из ∆ООА (ООА = 90º), используя теорему Пифагора ОО = , ОО =(см).

Ответ: 12 см.

Задача №20.

Площадь сечения шара плоскостью равна 64πсм². Радиус шара равен 17 см. Найдите расстояние от центра шара до плоскости сечения.

Решение.

Пусть дан шар с центром в точке О. Сечение шара плоскостью - круг с центром в точке О. Так как центр О этого круга есть основание опущенного на него перпендикуляра ОО, то ОО - расстояние от центра шара до заданного сечения. По условию площадь сечения .

Проведем радиус ОА = R, где А - точка, принадлежащая окружности сечения. По условию ОА = 17 см.

Площадь сечения , где r = ОА - радиус круга с центром в О. По условию , значит , ОА²=64, ОА= 5 см (ОА>0).

Из ∆ООА (ООА = 90º), используя теорему Пифагора ОО = , ОО =(см).

Ответ: 15 см.