Решение иррациональных уравнений (10 класс)

Урок алгебры и начала анализа

в 10 классе

Учитель:

Семендяева Людмила Вячеславовна

ГБОУ ЛНР

«Ровеньковская общеобразовательная школа №8»

Основные цели:

-обобщить и систематизировать знания и умения решать иррациональные уравнения различного вида и различными способами.

-развивать у учащихся внимание и аккуратность

-воспитывать усидчивость и трудолюбие

Одной из задач данного урока является повторение пройденного по теме "Иррарациональные уравнения" материала, подготовка учащихся к контрольной работе по данной теме.

1. Организационный момент.

2. Проверка домашнего задания:

а) Раздать карточки учащимся, которые садятся на первые парты, с индивидуальным заданием.

В этих карточках- часть домашней работы (для слабых учащихся).

Карточка №1 Карточка №2 Карточка №3

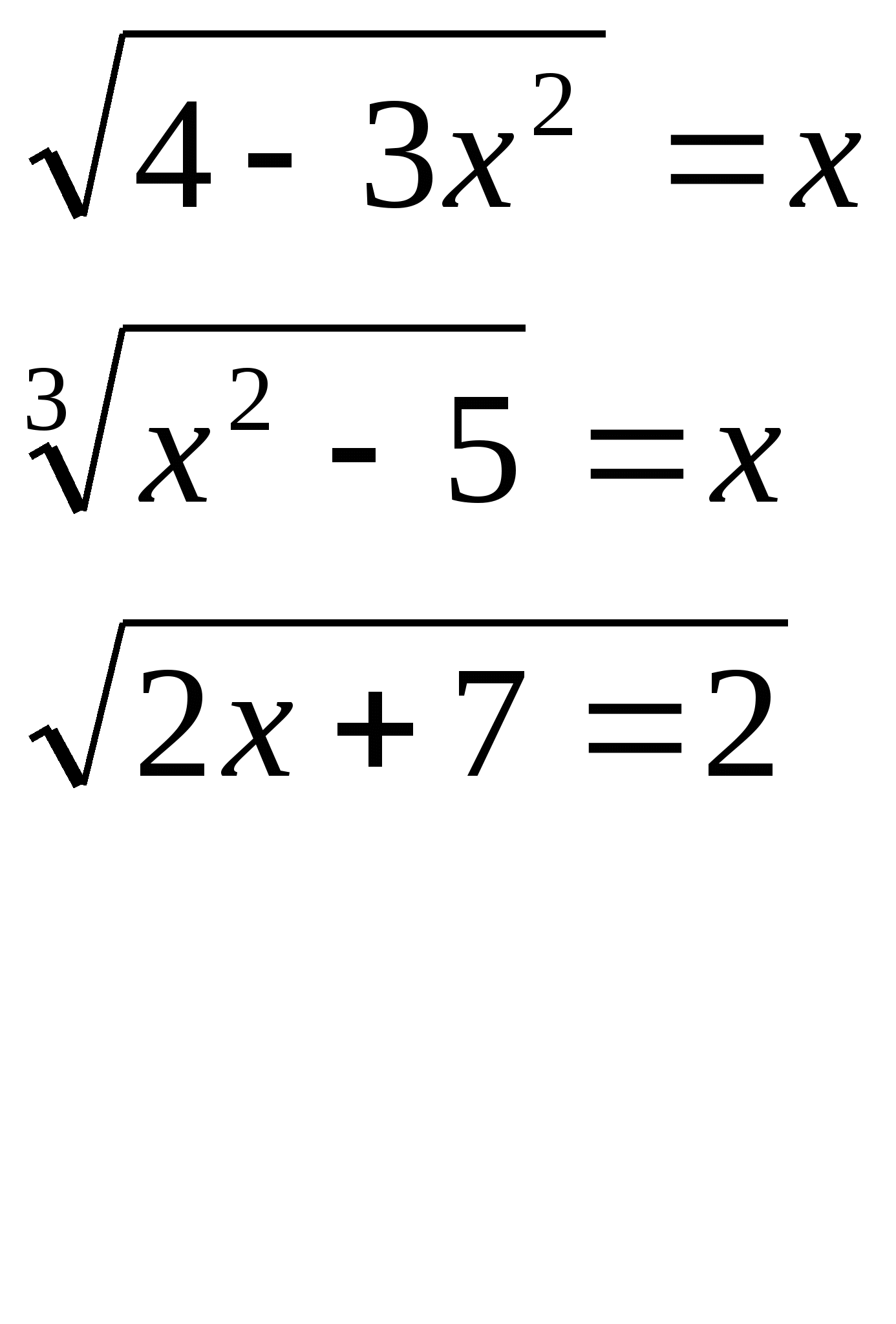
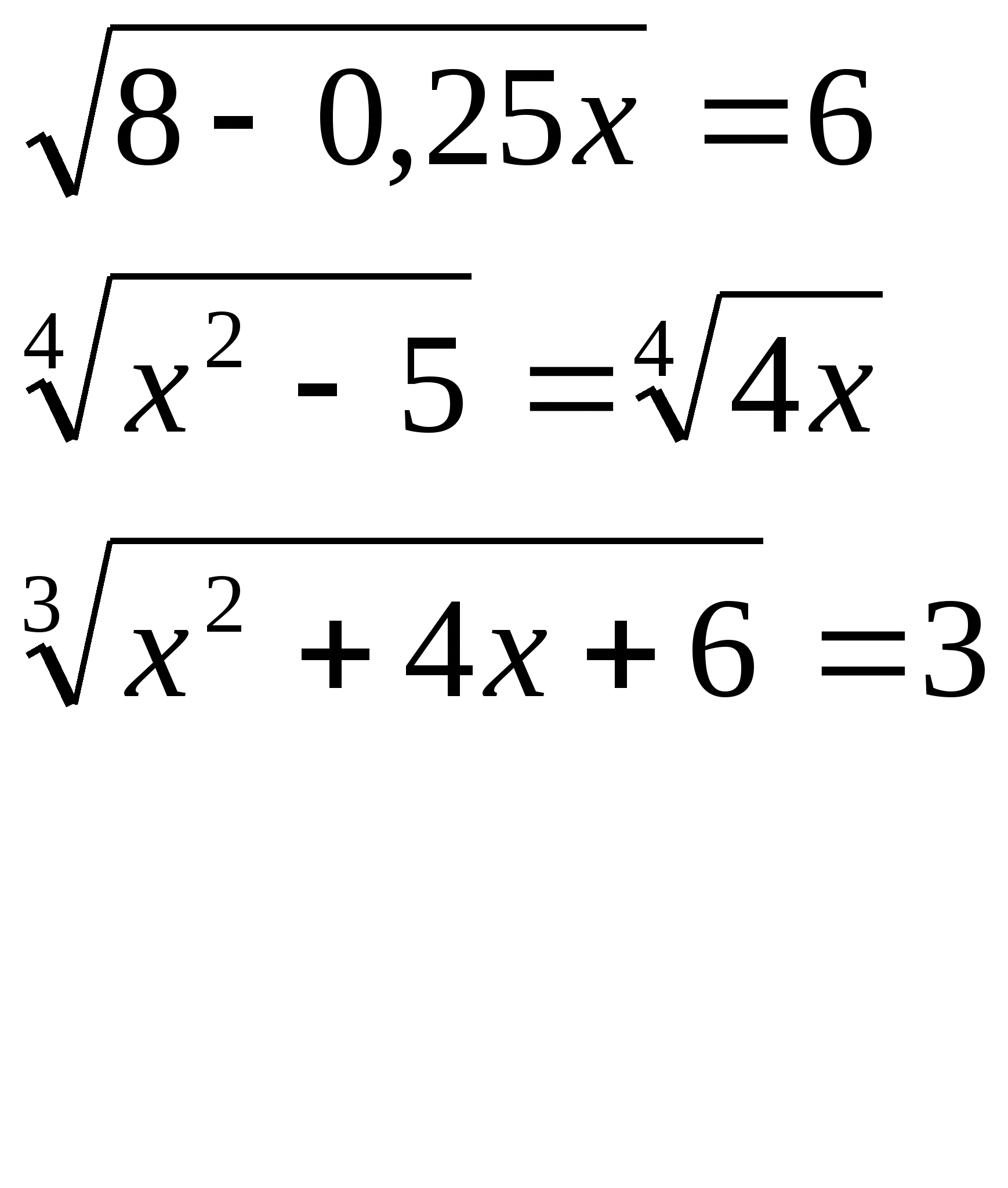
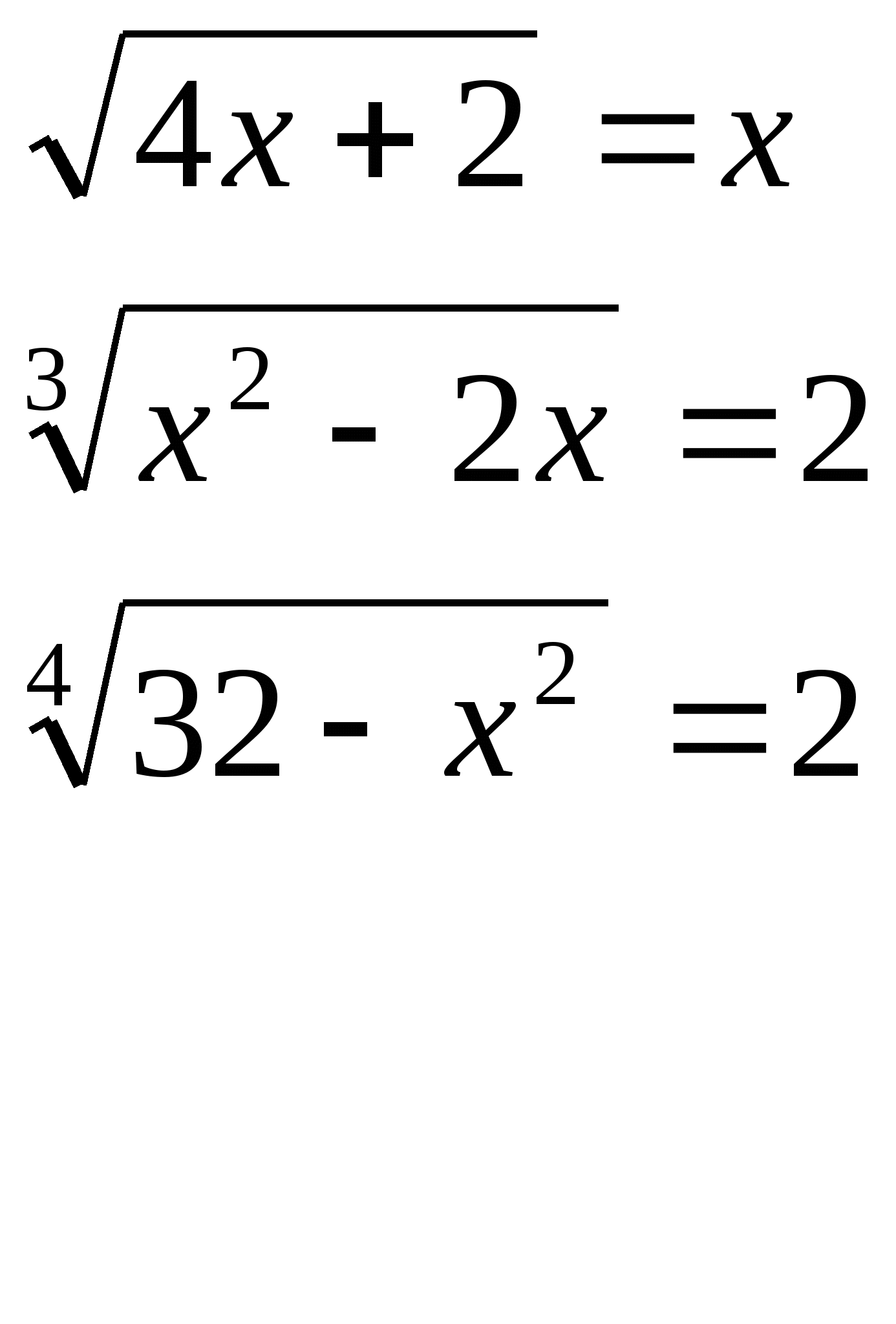
б) Вторая часть домашней работы проверяется на электронной доске. На доске выведены примеры с решением. Учащимся предлагается найти ошибку в решении, исправить её и объяснить.

№644(1) №644(3) №644(5)

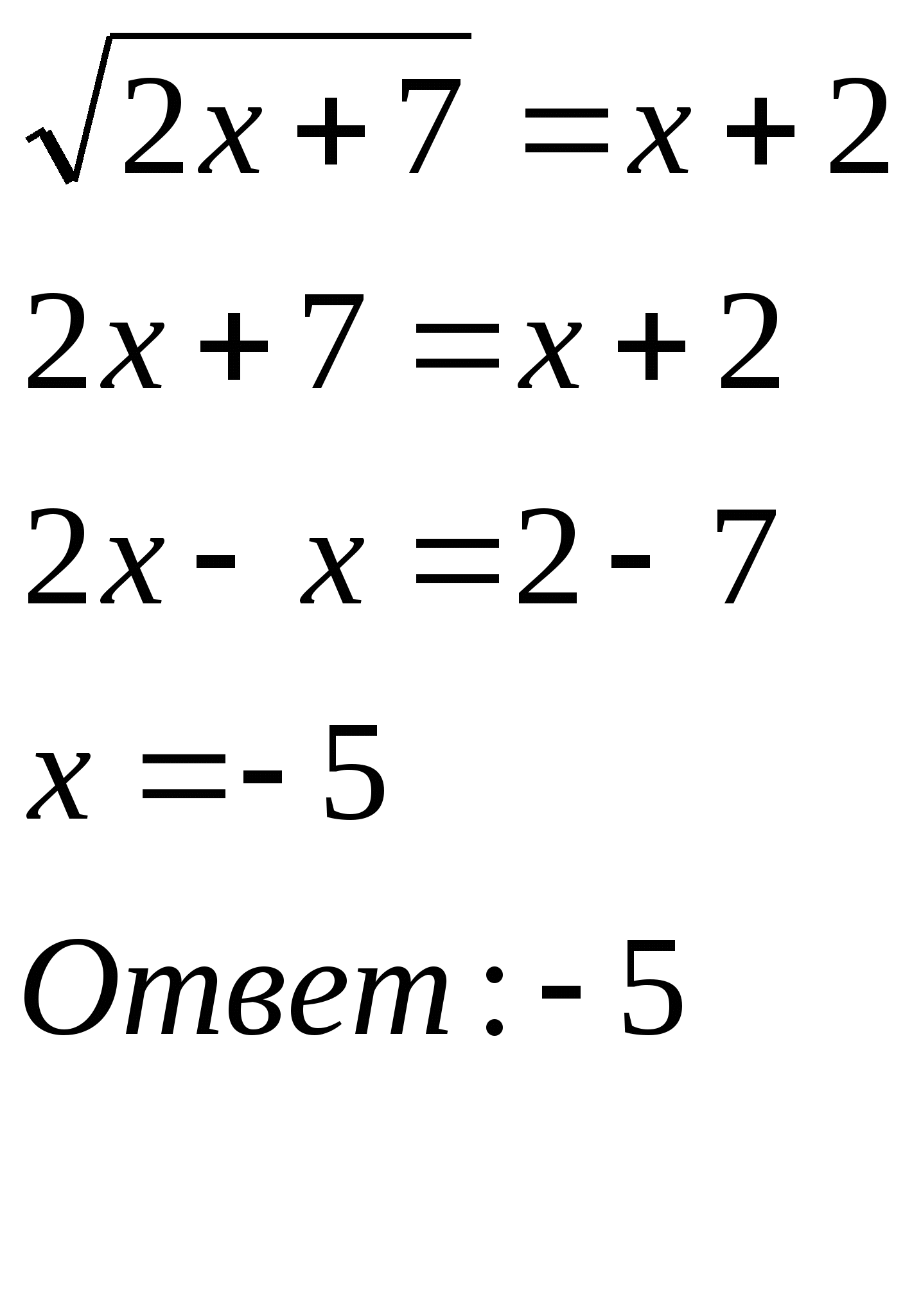
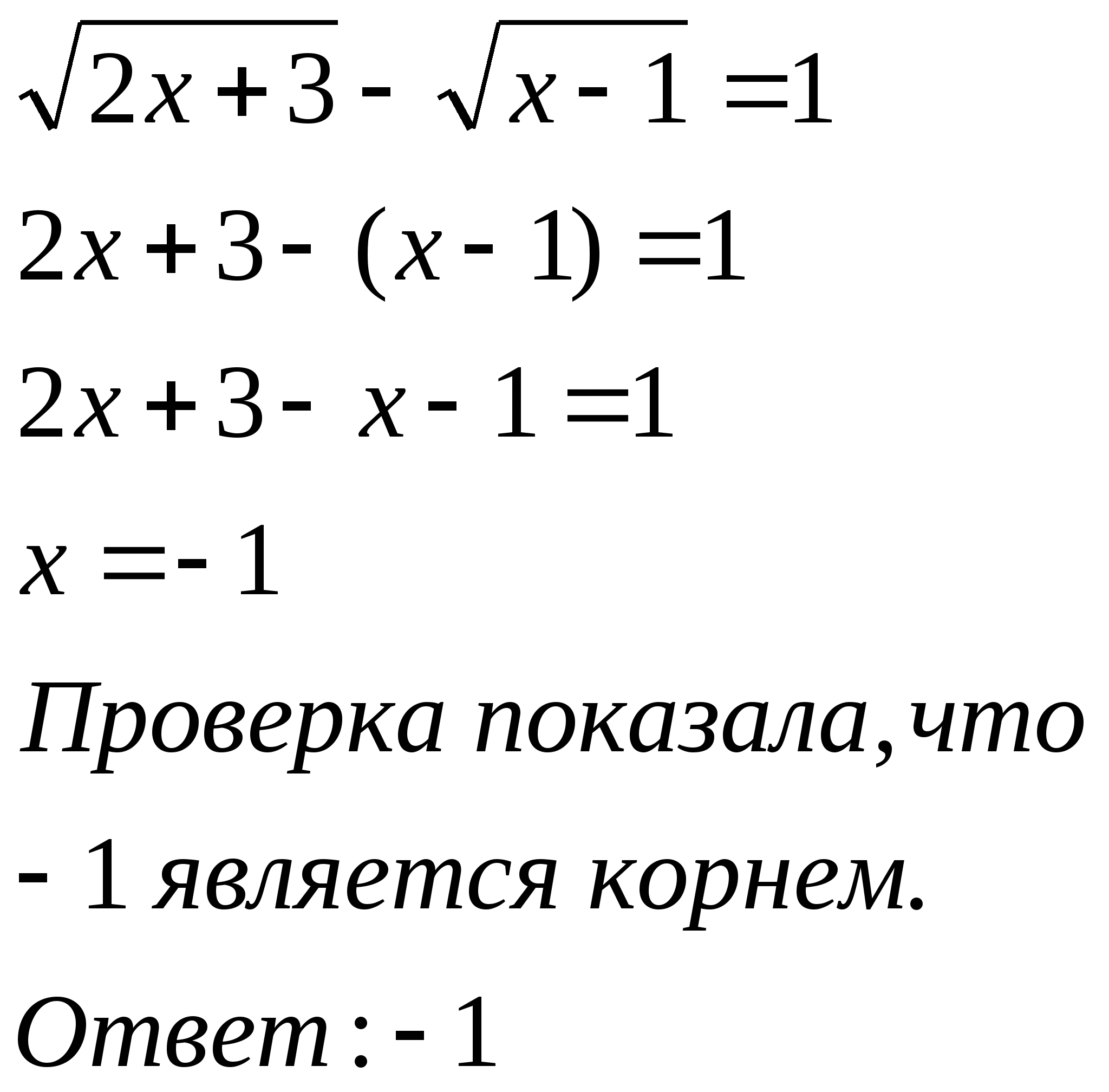
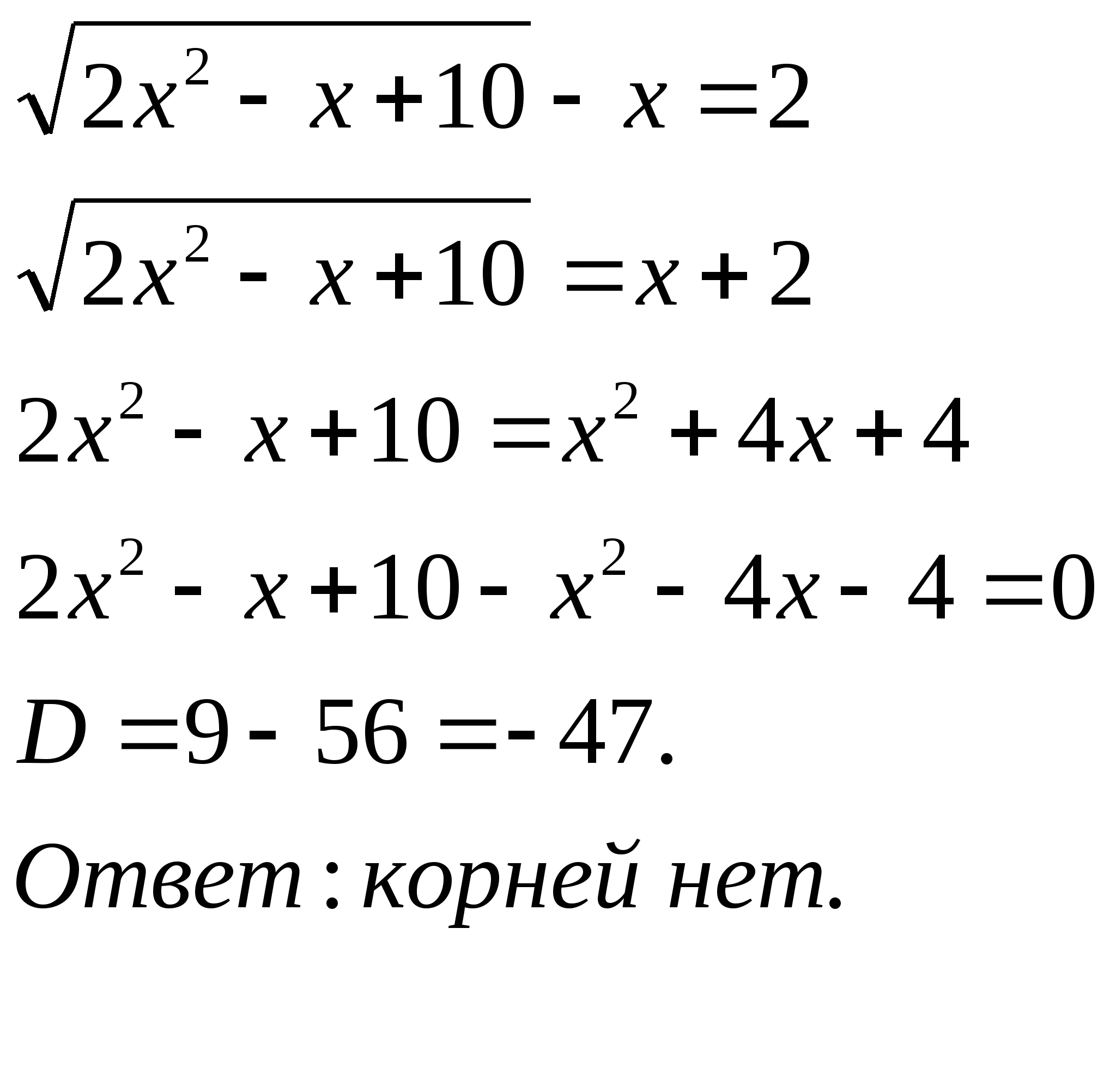
Вызванные 3 ученика исправляют ошибки:

№644(1) №644(3) №644(5)

2х+7=(х+2)² 2х+3-2+(х+1)=1 2x²-х+10-x²-4х-4=0

2х+7=x²+4х+4 3х+4-2 =1 x²-5х+6=0

x²+2х-3=0 3х+3=2 х1=3 х2=2

Проверка показывает 9x²+18х+9=8x²+20х+12 с учётом проверки

что, х=-3 не является x²-12х-3=0 Ответ: 3; 2

корнем х1=3 х2=-1

Ответ: 1 Проверка показывает,

что оба корня подходят

Ответ: 3 ; -1

3.Объявление темы: сегодня мы повторим способы решения иррациональных уравнений и начнем с самых простых.

4.Устный счет: 1) Решить уравнения:

а) (0,125) Что общего в этих уравнениях?

(-32) (корни нечётной степени)

(-26) Что можно сказать про подкоренное выражение?

(может быть любым числом)

(31) Что можно сказать про значение этого корня?

(может быть любым действительным числом)

б) (81) Что общего в этих уравнениях?

(24) (корни чётной степени)

(+1 и -1) Что можно сказать про подкоренное выражение?

(корней нет) (положительное или 0)

(1) Что можно сказать про значение этого корня?

(положительное или 0)

2) Представить в виде квадрата следующие выражения:

5. Запись числа, темы урока: "Решение иррациональных уравнений".

Решение уравнений:

Ученик №1

С чего обычно начинают решать иррациональные уравнения?

( с возведения в квадрат) Удобно ли это здесь? (нет)

Почему? (останется корень)

Упростим:

Решение с пояснениями О.О.У х>-1 Д.У. х>5

х-5=Öх+1

х 2-10х+25=х+1

х 2 -11х+24=0

х1=8 х 2=3 - вне Д.У.

Ответ: 8

Ученик №2

Сразу от корней не избавиться.

15-х+2+3-х=36 Возведём в квадрат дважды.

2=18+2х

=х+9

-18х+45=+18х+81

-36х=36

х=-1

Проверка: Л.ч. Ö15+1+Ö3+1=4+2=6

Пр. ч. 6 ; Л.ч.=Пр.ч.

Ответ: -1

Данный способ можно использовать не только с квадратными корнями, но и с корнями других степеней.

Ученик №3

О.Д.З.

+15=8(х+3) (-∞; +∞)

+15=8х+24

+8х-9=0

х1=9 х2=-1

Ответ: 9 ; -1

Ученик№4

О.Д.З.

+4х=32 (-∞; +∞)

+4х-32=0

х1=-8 х2=4

Ответ: 4 ; -8

Ученик №5

О.Д.З.

-5+16х-5=-6+12х-8 (-∞; +∞)

+4х+3=0

х1=-3 х2=-1

Ответ: -3 ; -1

Ученик№6

-3х=0

3+3х=0

3х(х+1)=0

х1=0 х2=-1

Проверка: х=0

Л.ч. =0 Пр. 0

Л.ч. =Пр. ч.

Л.ч. = Пр.ч. - не существует.

Ответ: 0

7.)Возьмем уравнения посложнее

Ребята такие уравнения подготовили дома:

Ученик№7

а) Д.У. х >0

3-2=

+2-3=0

Пусть =t, t>0 , тогда t2+2t-3=0

t1=-3, но t>0 , t2=1

Т.к. t2=1, то х2=1

х1=1 х1=-1 - вне Д.У.

Ответ: 1

Ученик№8

б) О.Д.З. х >1

Пусть =t, t>0 то тогда

2+t-3=0

t1=1,5 ,но t>0 t2=1

Т.к. t=1 , то =1

х-1=1

х=2

Ответ: 2

Ученик№9

в)

Пусть =t, t>0

то тогда

+3t-4=0

t1=-4 , но t>0, t2=1

Значит,

-3=1

=4

х1=2 х2=-2

Проверка: х1,2=±2

Л.ч.

П.ч. 0 Л.ч.=Пр.ч.

Ответ: 2 ;-2

6. Запишем домашнее задание:

№168(5), №169(3), №644(2,4), №645(1).

Индивидуально раздать карточки с заданиями на следующий урок, который продолжает эту тему.

Карточка №1

Карточка №2

Карточка№3

Ö11х+3-Ö2-х-Ö9х+7+Öх-2=0

7. Подведение итогов:

1)Как же решаются иррациональные уравнения?

Какие способы мы повторили?

(возведение в квадрат, замена переменной)

При решении этих уравнений всегда ли мы делаем равносильные преобразования?

Как уберечься от ошибки?

(следить за равносильностью преобразований или делать проверку)

2)Выставить оценки учащимся.