Урок по математике для 6 класса «Задачи на совместную работу»

Муниципальное бюджетное образовательное учреждение «СОШ №1»

Чугунова Татьяна Викторовна

Конспект урока

по математике 6 класс

тема: «Задачи на совместную работу»

Цели урока:

• сформировать понятие совместной работы;

• освоить обучающимися способ решения задач на совместную работу;

• составить алгоритма решения задач на совместную работу и закрепить его в ходе решения задач;

Задачи:

• актуализация уже накопленных знаний;

• создать условия для решения нового типа задач на совместную работу;

• создать ситуацию успеха;

В результате урока учащиеся должны:

Знать:

• понятия совместной работы;

• алгоритм решения задач на совместную работу;

Уметь:

• решать задачи на совместную работу;

1). Организационный момент.

Цель: Коррекция внимания обучающихся. И ориентирование на работу.

2). Актуализация знаний. Ситуация успеха.

Цель: проверка освоенности обучающимися раннее изученных способов решения; создание ситуации успеха, мотивирующей учащихся на дальнейшую работу.

Выстроим систему задач, готовящую к решению составной задачи. ( слайды №1- №6)

Давайте вспомним основные задачи по теме дроби, которые вы решали на предыдущих уроках.

А) Бассейн наполняется за 10 часов. Какая часть бассейна наполняется за 1 час?

( опираясь на понимание смысла дроби, проводят такие рассуждения:

Бассейн наполняется за 10 часов, значит, в час наполняется 1/10 бассейна)

Ответ: 1/10.

Б) В каждый час первая труба наполняет бассейн 1/10 бассейна, а вторая - 1/15 бассейна. Какую часть бассейна наполняют обе трубы за 1 час совместной работы?

Решение: 1/10+1/15=/16 часть бассейна наполняют обе трубы за 1 час.

Ответ: 1/6.

В) В каждый час труба наполняет 1/6 бассейна. За сколько часов она наполнит бассейн?

( В каждый час наполняется 1/6 бассейна, значит, весь бассейн наполнится за 6 часов.)

Ответ: 6 часов.

Третья задача (В) подводит нас к тому, что объем бассейна принимается за 1,

скорость наполнения равна 1/6, время заполнения равно 6 часам.

А сегодня мы рассмотрим еще один тип задач на дроби - это задачи на совместную работу.

Тема урока: «Задачи на совместную работу». (слайд №7)

3) По сути, обучающиеся подведены к решению такой задачи: (слайды №8-№10)

(задачу про бассейн решают в группах, решение проверяется).

Задача: В бассейн подведены две трубы. С помощью первой трубы бассейн можно наполнить за 10 ч, с помощью второй за - 5 ч. За сколько часов можно наполнить бассейн, если открыть обе трубы одновременно?

1. 1:10= 1/10 часть бассейна заполнит первая труба за час;

2. 1:5=1/5 часть бассейна заполнит вторая труба за час;

3. 1/10+1/5=3/10 части бассейна заполнят обе трубы за час, работая вместе;

4. Сколько времени потребуется, чтобы заполнить бассейн.

4).Формирование понятия совместной работы.

О какой работе идет речь в задаче? Что вы подразумеваете под совместной работой? Сколько субъектов может выполнять работу? Сколько времени потребуется для выполнения одной и той же работы, если ее выполнять индивидуально и совместно. В результате беседы выясняем, что такое совместная работа, и что задачи на движение навстречу друг другу, тоже относятся к задачам на совместную работу. А также, что при совместной работе складывают не время работы, а их производительности или скорости (например, для совместной работы двоих участников):

Объем бассейна (расстояние, выполненная работа и т. п.) принимается за 1 (единицу).

p (совместная)= p+p (v(совместная)= v+v)

A=P t ( S=Vt)

5).Составим алгоритм решения задачи в общем виде: (слайд №11)

1. Всю работу принять за единицу;

2. Найти, какая часть работы выполняется за единицу времени, то есть за один день, один час. Эта величина называется производительностью труда, то есть скорость выполнения работы (за1 день, за 1 час);

3) Найти общую производительность труда;

4) Найти время совместной работы.

6) Рефлексия действий по решению задач при помощи алгоритма.

Цель: зафиксировать в устной и письменной речи способ решения задач на совместную деятельность.

Задачи на работу в мастерской и на движение навстречу друг другу решают в парах (один из учеников является консультантом для другого) по вариантам. После чего, проверяем решение.

(слайды №12-№15)

Вариант №1

Задача: Библиотеке надо переплести некоторое количество книг. Первая мастерская может выполнить эту работу за 10 дней, а вторая - за 15 дней. За сколько дней выполнят эту работу мастерские, если будут работать вместе?

1)Какую часть работы выполнит первая мастерская за 1 день?

Ответ: 1: 10= 1/10 часть

2)Какую часть работы выполнит вторая мастерская за 1 день?

Ответ: 1: 15=1/15 часть

3) Какую часть работы выполнят обе мастерские за 1 день?

Ответ: 1/10 + 1/15= 1/6 часть

4)За сколько дней выполнят всю работу обе мастерские?

1 : 1/6= 6 дней.

Ответ: 6 дней

Вариант №2

Задача: Один велосипедист проезжает расстояние между двумя населенными пунктами за 2 часа, а другой велосипедист проезжает это же расстояние за 3 часа. Однажды оба велосипедиста одновременно выехали навстречу друг другу из этих населенных пунктов. Через сколько часов они встретятся?

1)1:2= 1/2 часть пути проезжает первый велосипедист за час;

2)1:3=1/3 часть пути проезжает второй велосипедист за час

3)1/2+1/3=5/6 частей пути проезжают оба велосипедиста за час, двигаясь навстречу друг другу;

4) Сколько времени потребуется велосипедистам, чтобы встретиться.

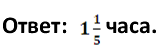
7)Закрепление изученного. Класс делится на две группы.

Первая группа (слабые учащиеся) выполняет две следующие задачи, дублирующие задачу, которая решалась в парах. Решают их самостоятельно при помощи алгоритма (раздаются карточки, проверяем решение через документ-камеру).

Задача №1

Через первую трубу можно наполнить бак за 10 мин, через вторую - за 15 мин. За сколько минут можно наполнить бак через обе трубы?

Задача №2

На птицеферму привезли корм, которого хватило бы уткам на 30 дней, а гусям на 45 дней. Рассчитайте, на сколько дней хватит привезенного корма уткам и гусям вместе?

Вторая группа, более подготовленные учащиеся, решают задачу с более сложной формулировкой (слайд №16). Если, учащимся трудно прийти к решению, то учитель может координировать их работу, задавая вопросы.

Задача. Первая бригада может выполнить задание за 9 дней, а вторая - за 12 дней. Первая бригада работала над выполнением этого задания 3 дня, потом вторая бригада закончила работу. За сколько дней было выполнено задание?

Вопрос учителя

Ожидаемый ответ учеников

Решение

Если первая бригада выполнила задание за 9 дней, то какую часть работы она выполнит за 1 день?

Какую часть задания выполнит первая бригада за 3 дня?

Умножить результат первого действия на 3.

Какую часть работы осталось доделать второй бригаде?

Какую часть задания выполнит вторая бригада за 1 день?

(1:12)

Сколько дней работала вторая бригада?

Результат третьего действия делим на результат четвёртого.

Сколько дней затрачено на выполнение задания?

11

3+8=11(дней)

8). Домашнее задание - решение задач по карточкам. (слайд №17)

Задача №1

Заготовленных материалов хватит для работы двух цехов в течение 10 дней или одного первого цеха в течение 15 дней. На сколько дней хватило бы этих материалов для работы одного второго цеха.

Задача №2

Из пунктов А и В одновременно навстречу друг другу вышли два пешехода. Они встретились через 40 мин после выхода, а через 32 мин после встречи первый пришёл в В. Через сколько часов после выхода из В второй пришел в А?

№640 стр 144 учебник Математика 6 класс/ И.И.Зубарева, А.Г.Мордкович.

9). Заключительный этап. слайд №18

• Подвести итог урока. Цель: проанализировать степень и качество достижения цели урока. Как вы считаете, умение решать задачи на совместную работу вам пригодится в жизни? (учащиеся высказывают свое мнение).

• Отметить активно работавших учащихся.

• Спасибо за работу!

Литература:

1. МАТЕМАТИКА. 6 класс/ И.И.Зубарева, А.Г.Мордкович.

2.Текстовые задачи в школьном курсе математики (5-9-е классы)/ А.В. Шевкин Москва Педагогический университет «Первое сентября» 2010.