- Учителю
- Настоящая рабочая программа разработана применительно к учебной программе А. Г. Мордковича «Алгебра» для 7-9 классов и ориентирована на использование учебно - методического комплекта: • Мордкович, А. Г. Алгебра. 8 класс: в 2 ч. Ч. 1: учебник для учащихся
Настоящая рабочая программа разработана применительно к учебной программе А. Г. Мордковича «Алгебра» для 7-9 классов и ориентирована на использование учебно - методического комплекта: • Мордкович, А. Г. Алгебра. 8 класс: в 2 ч. Ч. 1: учебник для учащихся
РАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ
2015-2016
учебный год
Класс: 8
Г. МОСКВА
2015
Пояснительная записка
Документы, на основании которых составлена программа:
1.Закон РФ «Об образовании в Российской Федерации» №273-ФЗ от 29.12.2012г.
2.Федеральный государственный образовательный стандарт основного общего образования (утвержден приказом Министерства образования и науки РФ № 1897 от 17.12.2010 г).
3.Примерная основная программа по математике;
4. Примерная учебная программа Мордковича А. Г. «Алгебра» для 7-9 классов.
5.Программа развития универсальных учебных действий на ступени основного общего образования.
6. Приказ Минобрнауки России от 31 марта 2014 г. № 253 «Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2014/15 учебный год"
7. Письмо Минобрнауки России от 24.11.11 № МД 1552/03 «Об оснащении общеобразовательных учреждений учебным и учебно - лабораторным оборудованием» (рекомендации по оснащению общеобразовательных учреждений учебным и учебно - лабораторным оборудованием, необходимым для реализации федерального государственного стандарта основного общего образования, организации проектной деятельности, моделирования и технического творчества обучающихся.
8.Федеральный базисный учебный план для ОУ РФ, реализующих программы общего образования.
Общая характеристика учебного предмета
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Практическая значимость школьного курса алгебры обусловлена тем, что для понимания принципов устройства и использования современной техники, восприятия научных и технических понятий и идей необходима хорошая математическая подготовка.
Алгебра является одним из опорных предметов основной школы: она обеспечивает изучение других дисциплин. В первую очередь это относится к предметам естественно-научного цикла, в частности к физике, информатике, химии. Развитие логического мышления и логической интуиции учащихся при обучении, умение аргументировать и обосновывать свои выводы и умозаключения, приводить чёткие определения, способствует также лучшему усвоению предметов гуманитарного цикла, что неоднократно отмечали мои коллеги - учителя английского и французского языков. Тем самым алгебра занимает ведущее место в формировании научно-теоретического мышления школьников.
Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Требуя от учащихся умственных и волевых усилий, концентрации внимания, активности развитого воображения, алгебра развивает нравственные черты личности (настойчивость, целеустремлённость, творческую активность, самостоятельность, ответственность, трудолюбие, дисциплину и критичность мышления) и умение аргументированно отстаивать свои взгляды и убеждения, а также способность самостоятельно принимать решения.
При обучении алгебры формируются умения и навыки умственного труда - планирование своей работы, поиск рациональных путей её выполнения, критическая оценка результатов.
Таким образом, в ходе освоения содержания курса, учащиеся получают возможность:
-
развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
-
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
-
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
-
развить логическое мышление и речь - умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
-
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Цели
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Для реализации программы используются следующие принципы:
-
Принцип развивающего обучения, обеспечивающий деятельностный характер образования, предполагающий отказ от механического усвоения учебного материала, от традиционного информационно-объяснительного подхода, ориентированного на передачу готовых знаний:
- Личностно - ориентированные принципы (принцип адаптивности, принцип развития, принцип психологической комфортности);
- Культурно- ориентированные принципы (принцип образа мира, принцип целостности содержания образования, принцип систематичности, принцип смыслового отношения к миру, принцип ориентировочной функции знаний, принцип овладения культурой);
- Деятельностно- ориентированные принципы (принцип обучения деятельности, принцип управляемого перехода от деятельности в учебной ситуации к деятельности в жизненной ситуации, принцип управляемого перехода от совместной учебно-познавательной деятельности к самостоятельной деятельности ученика, принцип опоры на предшествующее (спонтанное) развитие, креативный принцип).
-
Принцип дифференциации и индивидуализации, которые нацелены на создание возможностей для реализации индивидуальных образовательных траекторий, для удовлетворения интересов, склонностей и способностей учащихся, с учетом психофизиологических особенностей, здоровья, возрастных этапов их развития.
-
Принцип вариативности образования, который реализуется через переход от монопольной программы и учебника - к вариативному их набору, к введению интегрированных учебных курсов и программ; к введению различных вариантов дифференциации обучения, к усилению интегрированности учебного процесса на проектной основе.
-
Принцип непрерывности - обеспечивает преемственность различных ступеней образования.
Вышеперечисленные принципы, лежащие в основе построения программы, сориентированы на максимальный учет индивидуально-типологических особенностей учащихся, творческого саморазвития учащихся, создание на уроках условий для развития их внутреннего духовного мира и формирование целостной картины мира.
В основе реализации основной образовательной программы школы лежит системно-деятельностный подход, который предполагает:
- воспитание и развитие качеств личности, отвечающих требованиям информационного общества, инновационной экономики, задачам построения российского гражданского общества на основе принципов толерантности, диалога культур и уважения его многонационального, поликультурного и поликонфессионального состава;
- формирование соответствующей целям общего образования социальной среды развития обучающихся в системе образования, переход к стратегии социального проектирования и конструирования на основе разработки содержания и технологий образования, определяющих пути и способы достижения желаемого уровня личностного и познавательного развития обучающихся;
- ориентацию на достижение цели и основного результата образования; - развитие на основе освоения универсальных учебных действий, познания и освоения мира личности обучающегося, его активной учебно-познавательной деятельности, формирование его готовности к саморазвитию и непрерывному образованию;
- признание решающей роли содержания образования, способов организации образовательной деятельности и учебного сотрудничества в достижении целей личностного и социального развития обучающихся;
- учёт индивидуальных возрастных, психологических и физиологических особенностей обучающихся, роли, значения видов деятельности и форм общения при построении образовательного процесса и определении образовательно-воспитательных целей и путей их достижения.
Педагогические технологии, используемые при реализации образовательной программы, направлены на достижение современного качества образования, достижимого в условиях реализации новых ФГОС.
Выбор технологий определяется особенностями образования, направленного на развитие личности учащегося, реализации деятельностного подхода в обучении, изменению результативности образовательного процесса.
Педагогические технологии:
-
учебно-исследовательской деятельности;
-
проектной деятельности;
-
коллективный способ обучения;
-
проблемное обучение;
-
проблемно-диалогическая технология;
-
технология продуктивного чтения;
-
игровые технологии;
-
технология оценивания образовательных достижений;
-
кейс-метод;
-
ИКТ;
-
здоровьесберегающие технологии.
Наряду с основной формой обучения в школе используется индивидуально-групповая форма обучения. Индивидуальная форма обучения используется для проведения занятий с учащимися, пропустившими учебные занятия по болезни, имеющими психологические и логопедические проблемы и испытывающими трудности при изучении отдельных предметов.
Современное образование предусматривает значительное расширение роли информационных технологий как эффективного средства саморазвития, самосовершенствования и самообразования обучающихся. Умение находить и собирать информацию, проверять ее достоверность - первый шаг на пути к самостоятельной работе с информационными источниками, к самостоятельному продуцированию личностно значимой информации. Если раньше единственным источником информации был школьный учебник, то сегодня Интернет предоставляет информационное поле для поиска источников, которые далеко выходят за ограниченный объем школьного учебника. Для учащихся разработаны задания, требующие поиска, анализа и представления дополнительной информации по различным темам изучаемого курса в докладах, рефератах, исследовательских работах, что способствует формированию коммуникативных компетенций.
Кейс-метод - это метод анализа ситуаций (от англ.case-случай, ситуация). Под кейсом понимается детальное описание реального случая, причем ученикам предоставляется возможность проанализировать ситуацию, разобраться в проблеме, предложить свои пути разрешения проблемы и выбрать оптимальное решение. Основной задачей использования при обучении практического кейса является подробное и детальное отражение конкретной ситуации. Учебное назначение - тренинг обучаемых, закрепление знаний, умений, навыков. Основной задачей обучающих кейсов является отражение типовых ситуаций, с которыми сталкиваются специалисты в профессиональной деятельности. В основе стоят учебные и воспитательные задачи. Основной смысл научно-исследовательского кейса в том, что он является моделью для получения новых знаний о проблеме, ситуации и умения разрешать эту проблему. При использовании кейс-метода на уроках алгебры
-
Увеличивается количество заданий;
-
Повышается темп работы обучающегося;
-
Урок обогащается материалами, полученными из различных источников (в том числе из интернета);
-
Работа с кейсом носит характер ролевой игры, что повышает мотивацию учебной деятельности;
-
Достигается уровневая дифференциация обучения.
</ Проблемно диалогическое обучение - тип обучения, обеспечивающий творческое усвоение знаний учениками посредством специально организованного учителем диалога. На уроке изучения нового материала должны быть проработаны два звена: постановка учебной проблемы и поиск решения. Постановка учебной проблемы - это этап формулирования темы урока или вопроса для исследования. Поиск решения - это этап формулирования нового знания. Постановку учебной проблемы и поиск ее решения осуществляют ученики в ходе специально организованного учителем диалога.
У учащихся средних классов наблюдается рост интеллектуальных сил, стремление проникнуть в сущность изучаемых явлений, потребность в установлении причинно-следственных связей, включение в творческие виды деятельности и самообразования. Этому возрасту присуще взаимодействие и взаимопонимание. Именно на этот возраст чаще всего приходится становление предметных интересов и склонностей.
Основные условия, при которых формируется творческая математическая деятельность учащихся: организация обучения, при которой ученик вовлекается в процесс самостоятельного поиска и «открытия» новых знаний, решает задачи проблемного характера, понимает нужность, важность, целесообразность изучаемого материала в целом и отдельных его разделов. Учебный труд должен быть разнообразен, обучение должно быть трудным, но посильным. При составлении задач для самостоятельной работы, контрольных работ и тестов включаются задания, требующие от учащихся нестандартных подходов. Такие задания как правило оцениваются отдельной отметкой. Чем чаще проверяется и оценивается работа школьника (в том числе им самим), тем интереснее ему работать.
Основными целями использования групповых форм работы являются следующие:
1) активизация познавательной деятельности учащихся;
2) развитие учащихся (их логического и творческого мышления, поисковой направленности ума, самостоятельности, инициативности) с учетом их индивидуальных возможностей;
3) воспитание чувства коллективизма, коммуникабельности, коллективной ответственности за порученное дело, взаимовыручки;
4) достижение базового уровня знаний всеми категориями учеников, в том числе и «слабых»;
5) формирование общеинтеллектуальных умений и навыков (работа с учебной литературой; умение найти и сформулировать проблему, составить план ее решения, оценить полученные результаты; развитие деятельности наблюдения и другие);
6) развитие «педагогических и методических» качеств: умения внимательно выслушивать собеседника, проявлять терпение и спокойствие при объяснении непонятного другому человеку вопроса, доброжелательность.
Здоровьесберегающие факторы в процессе организации домашней самостоятельной работы реализуются по двум направлениям:
1) Нормирование времени (в том числе и за счет обучения приемам умственной деятельности) учащихся через выполнение дидактических требований учителями и учащимися к выполнению домашних заданий, а также через использование тетрадей на печатной основе, предназначенных специально для выполнения домашних заданий.
2) Усиление учебной мотивации в процессе домашней самостоятельной работы за счет внедрения альтернативных и дополнительных домашних заданий экспериментально-исследовательского, творческого и занимательного характера.
Настоящая рабочая программа разработана применительно к учебной программе А. Г.
Мордковича «Алгебра» для 7-9 классов и ориентирована на использование учебно -
методического комплекта:
-
Мордкович, А. Г. Алгебра. 8 класс: в 2 ч. Ч. 1: учебник для учащихся общеобразовательных учреждений ФГОС/ А. Г. Мордкович. - М.: Мнемозина, 2014.
-
Мордкович, А. Г. Алгебра. 8 класс: в 2 ч. Ч. 2: задачник для учащихся общеобразовательных учреждений ФГОС/А. Г. Мордкович [и др.]; под ред. А. Г. Мордковича. -М.: Мнемозина, 2014.
-
Мордкович, А. Г. Алгебра. 8 класс: метод, пособие для учителя / А. Г. Мордкович. - М. :
Мнемозина, 2010.
-
Александрова, Л. А. Алгебра. 8 класс: самостоятельные работы / Л. А. Александрова; под
ред. А. Г. Мордковича. - М.: Мнемозина, 2011.
-
Александрова, Л. А. Алгебра. 8 класс: контрольные работы / Л. А. Александрова; под
ред. А. Г. Мордковича. - М.: Мнемозина, 2011.
-
Мордкович, А. Г. Алгебра. 7-9 кл. тесты / А. Г. Мордкович, Е. Е. Тульчинская. - М. :
Мнемозина, 2011.
-
Рабочая тетрадь по алгебре. 8 класс. Часть 1. Часть 2. К учебнику А.Г. Мордковича "Алгебра. 8 класс". ФГОС, 2015 г. Ключникова Е.М., Комиссарова И.В. Издательство «Мнемозина».
-
Программы. Алгебра. 7-9 классы / авт.-сост., А. Г. Мордкович;
-
Е. Е. Тульчинская. Алгебра. 8 класс. Блицопрос;
-
В.В. Шеломовский. Электронное сопровождение курса «Алгебра-8» / Под ред. А. Г. Мордковича.
Структура учебника позволяет максимально облегчить учителю подготовку к уроку. Упражнения дифференцированы по трудности в четырех уровнях; в конце каждого параграфа сформулированы контрольные задания, позволяющие учителю сориентироваться в том, что должны знать и уметь учащиеся для достижения ими уровня стандарта математического образования; в конце учебника имеется раздел "Домашние контрольные работы", который поможет сориентировать учащихся на базовый уровень трудности. Теоретический материал подается так, чтобы помочь преподавателю в обеспечении проблемного подхода в обучении, в организации поисково-эвристической и коммуникативной деятельности учащихся.
Система упражнений, предлагаемая в Рабочих тетрадях, позволяет в
интересной, игровой форме организовать работу по формированию
навыков устных вычислений с применением различных приемов устной
работы на уроках, а также облегчить организацию и выполнение
домашних заданий, так как в каждом параграфе необходимо выполнить
задание на повторение теоретического материала, в каждом номере
есть подробный образец для выполнения данного задания.
В соответствии с требованиями ФГОС учебно-методический комплект
дополнен мультимедийным приложением - диском для учителя (для
использования при работе в классе). Диск содержит теоретический
материал, образцы графиков функций, образцы оформления решения
задач.
В основе реализации основной образовательной программы лежит
системно-деятельностный подход, в соответствии с чем, одним из
важнейших требований ФГОС является организация познавательной
деятельности учащихся через поисковую, исследовательскую, проектную
деятельность. С целью реализации этого требования в учебники
включены учебно-познавательные задания (задачи). Эти задания
отмечены специальным значком.
Таким образом, можно отметить следующие отличительные особенности учебников.
Во-первых, это реализация проблемного подхода в обучении. Учебный материал усваивается учащимися путем выполнения системы упражнений, цель которых - подвести ученика к самостоятельному выводу нового правила, алгоритма. Это помогает учителю организовать поисково-эвристическую и коммуникативную деятельность школьников.
Во-вторых, диалектический подход к введению математических понятий. Лишь простейшие понятия даются сразу в готовом виде, остальные же вводятся постепенно, с уточнениями и корректировкой, а некоторые вообще остаются на интуитивном уровне восприятия до тех пор, пока не наступит благоприятный момент для точного определения. К числу таких понятий относится, например, понятие функции. Во всяком случае, в этом учебнике, как и в учебнике для 7-го класса, строгого определения функции нет, оно будет введено лишь в курсе алгебры 9-го класса.
В-третьих, развивающее обучение. Приоритетным является не информационное, а развивающее поле курса. В учебнике реализованы практически все дидактические принципы развивающего обучения, сформулированные Л.В. Занковым: обучение на высоком уровне трудности; прохождение тем программы достаточно быстрым темпом; ведущая роль теоретических знаний; осознание собственного развития (учащийся должен видеть, как он умнеет в процессе изучения материала); развитие всех учащихся (естественно, учитывая, что у каждого учащегося свой потолок).
В-четвёртых, упражнения дифференцированы по четырем уровням сложности: задания на прямое применение алгоритма; задания, требующие некоторых простых рассуждений; задания, направленные на формирование у детей способности к усидчивости, развитие внимания, умения сосредоточиться. И наконец, задания, требующие от учащихся значительных умственных усилий - это задания на смекалку, текстовые задачи и т. д.
Содержание учебников соответствует федеральному компоненту государственного образовательного стандарта общего образования.
Общая характеристика учебного процесса.
Целью изучения курса алгебры в 8 классе является изучение квадратичной функции и её свойств, моделирующей равноускоренные процессы.
Задачи курса алгебры в 8 классе:
Выработать умение выполнять тождественные преобразования рациональных выражений.
Расширить класс функций, свойства и графики которых известны учащимся; продолжить формирование представлений о таких фундаментальных понятиях математики, какими являются понятия функции, её области определения, ограниченности. Непрерывности, наибольшего и наименьшего значений на заданном промежутке.
Выработать умение выполнять несложные преобразования выражений, содержащих квадратный корень, изучить новую функцию.
Навести определённый порядок в представлениях учащихся о действительных (рациональных и иррациональных) числах
Выработать умение выполнять действия над степенями с любыми целыми показателями.
Выработать умения решать квадратные уравнения и уравнения, сводящиеся к квадратным, и применять их при решении задач.
Выработать умения решать линейные и квадратные неравенства с одной переменной; познакомиться со свойствами монотонности функции.
Особенностью курса является то, что он является продолжением курса алгебры, который базируется на функционально- графическом подходе. Это выражается в том, что какой бы класс функций, уравнений и выражений не изучался, построение материала практически всегда осуществляется по жёсткой схеме: Функция - уравнения - преобразования.
Реализация данной программы способствует использованию разнообразных форм организации учебного процесса, внедрению современных методов обучения и педагогических технологий. Основной формой организации учебного процесса является классно-урочная система. В качестве дополнительных форм организации образовательного процесса в ОУ используется система консультационной поддержки, индивидуальных занятий, факультативные занятия, самостоятельная работа учащихся с использованием современных информационных технологий.
Используются следующие методы организации учебной деятельности:
-
создание проблемной ситуации и поиски решения проблемы на основе учебного материала по теме урока (проблемный диалог);
-
поисково-исследовательские методы;
-
выполнение самостоятельной работы (с учетом выбранной образовательной траектории);
-
работа в группах (парах) постоянного и переменного состава;
-
работа с текстом учебника «улучши и повтори»;
-
проверка домашнего задания «огонь по стоящим»;
-
игровые методы;
-
выполнение итоговых контрольных работ в форме тестов;
-
подготовка докладов и рефератов на основе отбора и анализа информации, с использованием дополнительной литературы (справочники и энциклопедии, сетевые ресурсы, электронные библиотеки и т.д.);
-
выступление с докладом; организация дискуссии и участие в дискуссии по итогам выступления;
-
выполнение творческих работ и их защита («Защита «звёздных» задач»);
-
организация коррекционной работы (группа «Консультант»).
В качестве форм промежуточной аттестации, учащихся используются традиционные диагностические и контрольные работы, блиц-опросы, результаты проектной и исследовательской деятельности, разноуровневые тесты, в том числе с использованием компьютерных технологий.
Описание места учебного предмета, курса в учебном плане
Для обязательного изучения учебного предмета Алгебра на этапе основного общего образования федеральный учебный базисный учебный план отводит 315 часов, в том числе 105 часа в VIII классе, из расчета 3 часа в неделю.
Личностные, метапредметные и предметные результаты.
Развитие УУД в основной школе целесообразно в рамках использования возможностей современной информационной образовательной среды как: средства обучения, повышающего эффективность и качество подготовки школьников, организующего оперативную консультационную помощь в целях формирования культуры учебной деятельности в ОУ; инструмента познания за счёт формирования навыков исследовательской деятельности, организации совместных учебных и исследовательских работ учеников и учителей, возможностей оперативной и самостоятельной обработки результатов экспериментальной деятельности; средства телекоммуникации, формирующего умения и навыки получения необходимой информации из разнообразных источников; средства развития личности за счёт формирования навыков культуры общения; эффективного инструмента контроля и коррекции результатов.
Развитие системы универсальных учебных действий в составе личностных, регулятивных, познавательных и коммуникативных действий, определяющих развитие психологических способностей личности, осуществляется с учётом возрастных особенностей развития личностной и познавательной сфер подростка.самоопределение (мотивация учения, формирование основ гражданской идентичности личности); смыслообразование («какое значение, смысл имеет для меня учение», и уметь находить ответ на него); нравственно- эстетическое оценивание (оценивание усваиваемого содержания, исходя из социальных и личностных ценностей, обеспечивающее личностный моральный выбор)
-
участие в проектах;
-
подведение итогов урока (рефлексия);
-
творческие задания;
-
мысленное воспроизведение картины, ситуации;
-
самооценка события;
-
дневники достижений
2
Познавательные УУД: общеучебные (формулирование познавательной цели; поиск и выделение информации; знаково-символические; моделирование); логические (анализ с целью выделения признаков (существенных, несущественных); синтез как составление целого из частей, восполняя недостающие компоненты; выбор оснований и критериев для сравнения, классификаций объектов; подведение под понятие, выведение следствий; установление причинно- следственных связей;
-
составление схем-опор;
-
работа с разного вида таблицами;
-
составление и распознавание диаграмм
-
построение и распознавание графиков функций
-
умение проводить классификации, логические обоснования, доказательства математических утверждений;
-
овладение основными способами представления и анализа статистических данных, наличие представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о вероятностных моделях;
-
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
3
Регулятивные УУД:
Целеполагание
Планирование
Прогнозирование
Контроль
Коррекция
Оценка
Волевая саморегуляция
-
постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще неизвестно;
-
определение последовательности промежуточных целей с учетом конечного результата;
-
составление плана и последовательности действий;
-
предвосхищение результата уровня усвоения, его временных характеристик;
-
в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;
-
внесение необходимых дополнений и корректив в план и способ действия в случае расхождения эталона, реального действия и его продукта;
-
выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения;
-
способность к мобилизации сил и энергии; способность к волевому усилию - к выбору в ситуации мотивационного конфликта и к преодолению препятствий
4
Коммуникативные УУД:
планирование
постановка вопросов
разрешение конфликтов
управление поведением партнера точностью выражать свои мысли
-
определение цели, функций участников, способов взаимодействия;
-
инициативное сотрудничество в поиске и сборе информации;
-
выявление, идентификация проблемы, поиск и оценка альтернативных способов разрешения конфликта, принятие решения и его реализация;
-
контроль, коррекция, оценка действий партнера, умение с достаточной полнотой и точностью выражать свои мысли
Содержание учебного предмета «Алгебра - 8»
Повторение курса алгебры за 7 класс
Алгебраические дроби
Понятие алгебраической дроби. Рациональное выражение. Допустимые значения дробного выражения. Основное свойство алгебраической дроби. Сокращение алгебраических дробей. Приведение дроби к заданному знаменателю. Способ группировки и вынесение общего множителя за скобки при приведении дробей к общему знаменателю. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями. Алгоритм сложения (вычитания) алгебраических дробей с одинаковыми знаменателями. Сложение и вычитание алгебраических дробей с разными знаменателями. Сложение и вычитание целого выражения и дроби. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень. Рациональное выражение (целое, дробное). Доказательство тождеств. Преобразование рациональных выражений Рациональное уравнение. Решение рациональных уравнений (первые представления). Область допустимых значение рациональных уравнений.
Квадратичная функция y = kx2. Гипербола .
Функция y = kx2, ее график, свойства. Построение графика функции y = kx2. Функция , ее свойства и график. Гипербола. Асимптота. Решение уравнений и систем уравнений графическим способом. Способ построения графика функции y = f (x+l) по известному графику функции y = f (x). Способ построения графика функции y = f (x) + m по известному графику функции y = f (x). Способ построения графика функции y= f (x+l) + m, y = -f (x) по известному графику функции y = f (x). Квадратный трехчлен. Квадратичная функция, ее свойства и график. Алгоритм построения графика квадратичной функции. Понятие ограниченной функции. Построение и чтение графиков кусочных функций. Графическое решение квадратных уравнений.
Функция y=√x. Свойства квадратного корня
Рациональные числа. Рациональные числа и их свойства. Понятие квадратного корня из неотрицательного числа. Понятие кубического корня. Правила вычисления. Корень n-й степени из неотрицательного числа. Иррациональные числа. Действия с иррациональными числами. Множество действительных чисел. Изображение действительных чисел на числовой прямой. Функция y=√x, ее свойства и график. Выпуклость функции. Область значений функции. Свойства взаимного обратных функций. Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Освобождение от иррациональности в знаменателе дроби. Модуль действительного числа. Основные свойства модуля числа. График функции y =√x.
Квадратные уравнения (21 ч.)
Квадратное уравнение. Приведенное (неприведённое) квадратное уравнение. Полное (неполное) квадратное уравнение. Корень квадратного уравнения. Решение квадратного уравнения методом разложения на множители, методом выделения полного квадрата. Дискриминант. Формулы корней квадратного уравнения. Параметр. Уравнение с параметром (начальные представления). Алгоритм решения рационального уравнения. Биквадратное уравнение. Метод введения новой переменной. Рациональные уравнения как математические модели реальных ситуаций. Решение текстовых задач с помощью рациональных уравнений. Частные случаи формулы корней квадратного уравнения. Теорема Виета. Разложение квадратного трехчлена на линейные множители. Иррациональное уравнение. Метод возведения в квадрат.
Действительные числа
Рациональные, иррациональные, действительные числа. Множество действительных чисел. Делимость чисел. Признаки делимости. Среднее арифметическое, среднее геометрическое чисел. Приближенные значения действительных чисел, погрешность приближения, приближение по недостатку и избытку. Округление чисел. Степень с натуральным и степень с отрицательным показателем. Стандартный вид положительного числа.
Неравенства
Свойства числовых неравенств. Сравнение чисел и выражений с помощью свойств числовых неравенств. Возрастающая функция. Убывающая функция. Исследование функций на монотонность. Неравенство с одной переменной. Решение неравенств с одной переменной. Линейное неравенство. Равносильные неравенства. Равносильное преобразование линейного неравенства. Графический способ решения линейных неравенств. Квадратное неравенство. Алгоритм решения квадратного неравенства.
Обобщающее повторение курса алгебры за 8 класс
Название темы
Характеристика основных видов деятельности учащихся
1
Повторение курса 7 класса
Повторяют понятия: степень одночлена, стандартный вид многочлена, действия над многочленами, формулы сокращённого умножения, линейная функция, системы линейных уравнений с двумя переменными;
Раскладывают многочлены на множители различными способами, строят графики линейных функций, находят значения функции по заданному аргументу, решают линейные уравнения, решают системы линейных уравнений способами подстановки и сложения, выбирают рациональный способ решения, проводят сравнительный анализ, осуществляют проверку выводов.
2
Алгебраические дроби
2.1
Основные понятия
Имеют представление о числителе, знаменателе алгебраической дроби, о значении алгебраической дроби, о значении переменной, при которой алгебраическая дробь не имеет смысла; знают, как распознавать алгебраические дроби, как найти допустимые значения переменной алгебраической дроби;
Находят рациональным способом значение алгебраической дроби, устанавливают, при каких значениях переменной алгебраическая дробь не имеет смысла, аргументированно обосновывают свое решение, осмысливают и устраняют свои ошибки.
2.2
Основное свойство алгебраической дроби
Знают правила разложения на множители, основное свойство дроби;
Раскладывают многочлен на множители несколькими способами, преобразовывают алгебраические дроби к одному знаменателю, работают по алгоритму сокращения дробей, доказывают правильность решения с помощью аргументов.
2.3
Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
Знают, как складывать и вычитать дроби с одинаковыми знаменателями, алгоритм сложения дробей с одинаковыми знаменателями;
Находят все натуральные значения переменной, при которых заданная дробь является натуральным числом, составляют конспект, складывают и вычитают дроби с одинаковыми знаменателями, проводят сравнительный анализ.
2.4
Сложение и вычитание алгебраических дробей с разными знаменателями
Получают представление о наименьшем общем знаменателе, о дополнительном множителе, о выполнении действия сложения и вычитания дробей с разными знаменателями.
Знают правило приведения алгебраических дробей к общему знаменателю, как находить общий знаменатель нескольких дробей, алгоритм сложения и вычитания дробей с разными знаменателями, как добывать информацию по заданной теме в источниках различного типа.
Упрощают выражения наиболее рациональным способом, применяя формулы сокращенного умножения, доказывают тождества, участвуют в диалоге, понимают точку зрения собеседника, признают право на иное мнение; излагают информацию, интерпретируя факты, разъясняя значение и смысл теории; работают с текстами научного стиля
2.5
Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень.
Получают представление об умножении и делении алгебраических дробей, о возведении их в степень.
Знают правило выполнения действий умножения и сложения алгебраических дробей; как пользоваться алгоритмами умножения и деления дробей, возведения дроби в степень, упрощая выражения.
Упрощают выражения наиболее рациональным способом, применяя формулы сокращенного умножения, доказывают тождества, развернуто обосновывают суждения, формулируют выводы, дают определения, приводят доказательства, примеры; излагают информацию, интерпретируя факты, разъясняя значение и смысл теории, вступают в речевое общение, участвуют в диалоге.
2.6
Преобразование рациональных выражений
Получают представление о преобразовании рациональных выражений, используя все действия с алгебраическими дробями. Знают способы преобразования рациональных выражений с алгебраическими дробями.
Выполняют преобразования рациональных выражений, используя все действия с алгебраическими дробями, решают рациональные уравнения, доказывают тождества, решают задачи, выделяя три этапа математического моделирования, используют для решения познавательных задач справочную литературу, воспроизводят изученные правила и понятия, подбирают аргументы, соответствующие решению, осуществляют проверку выводов, положений, закономерностей, теорем, составляют план действий, приводят примеры, формулируют выводы, вопросы, задачи, создают проблемную ситуацию, развернуто обосновывают суждения, воспроизводят теорию с заданной степенью свернутости;
2.7
Первые представления о рациональных уравнениях
Получают представление о рациональных уравнениях, об освобождении от знаменателя при решении уравнений, о составлении математической модели реальной ситуации.
Решают рациональные уравнения, применяя формулы сокращенного умножения при их упрощении, решают проблемные задачи, составляют и решают задачи, выделяя три этапа математического моделирования, излагают информацию, интерпретируя факты, участвуют в диалоге, понимают точку зрения собеседника, признают право на иное мнение, аргументированно отвечают на вопросы собеседников.
3
Квадратичная функция. Функция у=k/х
3.1
Функция у=kх2, у=k/х, их свойства и графики. Преобразование графиков
Получают представление о функции вида ![]() , о ее графике и свойствах. о функции вида
, о ее графике и свойствах. о функции вида ![]() , о ее графике и свойствах. Знают, как строить график функции
, о ее графике и свойствах. Знают, как строить график функции
![]() , функции
, функции ![]() , свойства функции. Получают представление, как с помощью
параллельного переноса вправо или влево построить график функции
, свойства функции. Получают представление, как с помощью
параллельного переноса вправо или влево построить график функции
у = f(x + l), как с помощью параллельного переноса вверх или вниз построить график функции у = f(x) + m,
как с помощью параллельного переноса вверх или вниз построить график функции у = f(x + l) + m. Знают, как строить график функции вида
у = f(x + l) + m, описывать свойства функции по ее графику.
Графически решают уравнения и системы уравнений, графически определяют число решений системы уравнений, упрощают функциональные выражения, строят графики кусочно-заданных функций, решают нетиповые задачи с помощью графического метода, выполняя продуктивные действия эвристического типа; воспроизводят теорию с заданной степенью свернутости, осуществляют проверку выводов, положений, закономерностей, теорем, работают с чертежными инструментами.
По алгоритму строят график функции
у = f(x + l), у = f(x) + m, у = f(x + l) + m, у = а(x + l)2 + m, читают и описывают свойства графика, самостоятельно исправляют допущенные ошибки или неточности; принимают участие в диалоге, подбирают аргументы для объяснения ошибки, классифицируют и проводят сравнительный анализ, рассуждают и обобщают.
3.2
Функция у=ах2+вх+с, её свойства и график
Получают представление о функции
у = аx2 + bx + с, о ее графике и свойствах. Знают, как
строить график функции у = аx2 + bx + с, описывать ее
свойства по графику. Знают способы решения квадратных уравнений,
применяют их на практике.
Умеют переходить с языка формул на язык графиков и наоборот, определять число корней уравнения и системы уравнений, приводить примеры, подбирать аргументы, формулировать выводы; упрощают функциональные выражения, находят значения коэффициентов в формуле функции
у = аx2 + bx + с без построения графика функции, работают с чертежными инструментами, применяют несколько способов графического решения уравнений; на основе комбинирования ранее изученных алгоритмов и способов действия решают нетиповые задачи, выполняя продуктивные действия эвристического типа
4
Функция у=х. Свойства квадратного корня
4.1
Свойства квадратных корней
Получают представление о способе извлечения квадратного корня из
неотрицательного числа, действительных и иррациональных числах, как
строить график функции ![]() , знают ее свойства. Знают свойства квадратных корней.
, знают ее свойства. Знают свойства квадратных корней.
Решают квадратные уравнения, корнями которых являются иррациональные числа, и простейшие иррациональные уравнения, читают графики функций, решать графически уравнения и системы уравнений, применяют данные свойства корней при нахождении значения выражений, выполняют более сложные упрощения выражений наиболее рациональным способом, вычисляют значения квадратных корней, не используя таблицу квадратов чисел, решают функциональные уравнения, вступают в речевое общение, участвуют в диалоге, излагают информацию, обосновывая свой собственный подход, воспроизводят изученные правила и понятия, подбирают аргументы, соответствующие решению.
4.2
Преобразование выражений, содержащих операцию извлечения квадратного корня
Получают представление о преобразовании выражений, об операциях извлечения квадратного корня и освобождения от иррациональности в знаменателе. Знают, как выполнять преобразования, содержащие операцию извлечения корня, освобождаться от иррациональности в знаменателе. Раскладывают выражения на множители способом группировки, используя определение и свойства квадратного корня, формулы квадратов суммы и разности, оценивают неизвлекаемые корни, находят их приближенные значения, выполняют преобразования иррациональных выражений, сокращают дроби, раскладывая выражения на множители, освобождаются от иррациональности в знаменателе, свободно работают с текстами научного стиля, формулируют выводы, участвуют в диалоге, понимают точку зрения собеседника, признают право на иное мнение., осуществляют проверку выводов, положений, закономерностей, теорем.
5
Квадратные уравнения
5.1
Формулы корней квадратного уравнения
Получают представление о полном
и неполном квадратном уравнении, о решении неполного квадратного
уравнения, о дискриминанте квадратного уравнения, формулах корней
квадратного уравнения, об алгоритме решения квадратного уравнения.
Знают, как решать неполные квадратные уравнения и полные квадратные
уравнения, разложив левую часть на множители. Знают алгоритм
вычисления корней квадратного уравнения, используя дискриминант,
как решать квадратные уравнения по формулам корней квадратного
уравнения через дискриминант.
Решают любые квадратные уравнения: приведенные полные, неприведенные полные, неполные; решают рациональные уравнения и задачи на составление рациональных уравнений, выводят формулы корней квадратного уравнения, если второй коэффициент нечетный, решают простейшие квадратные уравнения с параметрами и проводят исследование всех корней квадратного уравнения с параметром, решают задачи на составление квадратных уравнений, проводят сравнительный анализ, сопоставляют, рассуждают, свободно работают с текстами научного стиля, участвуют в диалоге, понимают точку зрения собеседника, признают право на иное мнение.
5.2
Рациональные уравнения
Получают представление о рациональных уравнениях и способах их
решения, как решаются рациональные уравнения по заданному алгоритму
и методом введения новой переменной. Знают алгоритм решения
рациональных уравнений, алгоритм вычисления корней квадратного
уравнения с четным вторым коэффициентом. Решают рациональные
уравнения, используя метод введения новой переменной, решают
простейшие квадратные уравнения с четным вторым коэффициентом с
параметрами и проводить исследование всех корней квадратного
уравнения с четным вторым коэффициентом с параметром, работают по
заданному алгоритму, доказывают правильность решения с помощью
аргументов. Решают задачи на числа, задачи на движение по дороге,
задачи на движение по воде, выделяя основные этапы математического
моделирования. Решают биквадратные уравнения, развернуто
обосновывают суждения, приводят доказательства,
в том числе от противного. Аргументированно отвечают на
поставленные вопросы, осмысливают ошибки и устраняют их.
5.3
Иррациональные уравнения
Получают представление о теореме Виета и об обратной теореме Виета, о симметрических выражениях с двумя переменными, об иррациональных уравнениях, равносильных уравнениях, о равносильных преобразованиях уравнений, о неравносильных преобразованиях уравнений.
Применяют теорему Виета и обратную теорему Виета для решения квадратных уравнений. Умеют, не решая квадратного уравнения, вычислять выражения, содержащие корни этого уравнения в виде неизвестных, применяя обратную теорему Виета; обосновывать суждения, давать определения, приводить доказательства, примеры. Составляют квадратные уравнения по их корням, раскладывают на множители квадратный трехчлен, решают иррациональные уравнения, совершая равносильные переходы в преобразованиях, проверяют корни, получившиеся при неравносильных преобразованиях, составляют конспект, проводят сравнительный анализ, сопоставляют, рассуждают, воспроизводят теорию с заданной степенью свернутости, принимают участие в диалоге, подбирают аргументы для объяснения ошибки.
6
Действительные числа
6.1
Множество действительных чисел
Знают понятия рационального числа, бесконечной десятичной
периодической дроби, понятие «иррациональное число», знают о
делимости целых чисел;
о делении с остатком, определение модуля действительного числа.
Умеют определять понятия, приводят доказательства, формулировать полученные результаты, доказывать иррациональность числа, любое рациональное число записывают в виде конечной десятичной дроби и наоборот, доказывают и применяют свойства модуля, решают модульные неравенства, передают информацию сжато, полно, выборочно (в зависимости от ситуации), осуществляют проверку выводов, положений, закономерностей, теорем; работают с учебником, отбирают и структурируют материал, находят и используют информацию, уверенно действуют в нетиповой, незнакомой ситуации, самостоятельно исправляя допущенные при этом ошибки или неточности, используют для решения познавательных задач справочную литературу, проводят самооценку собственных действий, составляют конспект, проводят сравнительный анализ.
6.2
Степень с отрицательным показателем
Получают представление о степени с натуральным показателем, о степени с отрицательным показателем, об умножении, делении и возведении в степень степени числа; знают о приближенном значении по недостатку, по избытку, об округлении чисел, погрешности приближения, абсолютной и относительной погрешностях, о стандартном виде положительного числа, о порядке числа, о записи числа в стандартной форме. Упрощают выражения, используя определение степени с отрицательным показателем и свойства степени, выполняют более сложные преобразования выражений, содержащих степень с отрицательным показателем, доказывают тождества;
используют знания о приближенном значении по недостатку, по избытку, об округлении чисел, погрешности приближения, абсолютной и относительной погрешностях при решении задач, аргументированно отвечают на поставленные вопросы, осмысливают и устраняют ошибки.
7
Неравенства
7.1
Решение линейных неравенств
Знают свойства числовых неравенств.
Получают представление о неравенстве одинакового смысла, противоположного смысла, о среднем арифметическом и среднем геометрическом, о неравенстве Коши. Знают, как применять свойства числовых неравенств и неравенство Коши при доказательстве числовых неравенств. Получают представление о неравенстве с переменной, о системе линейных неравенств, пересечении решений неравенств системы. Знают, как решать неравенства с переменной и системы неравенств с переменной.
Доказывают справедливость числового неравенства методом выделения квадрата двучлена и используя неравенство Коши, доказывают справедливость числовых неравенств при любых значениях переменных, выполняют действия с числовыми неравенствами, развернуто обосновывают суждения, приводят доказательства, в том числе от противного, изображают на координатной плоскости точки, координаты которых удовлетворяют неравенству, аргументированно отвечают на поставленные вопросы, участвуют в диалоге, оформляют полностью или сокращают решения в зависимости от ситуации.
7.2
Решение квадратных неравенств
Получают представление о квадратном неравенстве, о знаке объединения множеств, алгоритме решения квадратного неравенства, о методе интервалов, о решении квадратных неравенств с параметром. Знают, как решать квадратное неравенство по алгоритму и методом интервалов.
Решают квадратные неравенства методом интервалов, работают по заданному алгоритму, доказывают правильность решения с помощью аргументов, решают квадратные неравенства, применяя равносильные преобразования выражений, решают квадратные неравенства с параметром, объясняют изученные положения на самостоятельно подобранных конкретных примерах, излагают информацию, интерпретируя факты, разъясняя значение и смысл теории; составляют план выполнения построений.
7.3
Исследование функции на монотонность
Получают представление о возрастающей, убывающей, монотонной функции на промежутке. Знают, как построить и исследовать на монотонность функции: линейную, квадратную, обратной пропорциональности, функцию корня.
Исследуют различные функции на монотонность, решают уравнения и неравенства, используя свойство монотонности, осуществляют проверку выводов, положений, закономерностей, теорем, исследуют кусочно-заданные функции на монотонность, составляют конспект, проводят сравнительный анализ.
8
Обобщающее повторение курса алгебры за 8 класс
Проводят самоанализ знаний, умений и навыков, полученных и приобретенных в курсе алгебры за 8 класс при обобщающем повторении тем: «Алгебраические дроби», «Квадратные уравнения», «Неравенства».
Для этого необходимо овладеть умениями:
- использовать приобретенные знания и умения в практической деятельности
Итого
Планируемые результаты
Алгебраические дроби
Выпускник научится:
-
осуществлять в рациональных выражениях числовые подстановки и выполнять соответствующие вычисления;
-
выполнять действия сложения и вычитания с алгебраическими дробями;
-
сокращать дробь;
-
возводить дробь в степень;
-
выполнять действия умножения и деления с алгебраическими дробями;
-
выполнять разложение многочлена на множители применением формул; сокращенного умножения;
-
выполнять преобразование рациональных выражений;
-
решать простейшие рациональные уравнения;
-
понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
-
устанавливать, при каких значениях переменной алгебраическая дробь не имеет смысла.
Выпускник получит возможность научиться:
-
выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов;
-
выбирать рациональный способ решения;
-
давать определения алгебраическим понятиям;
-
работать с заданными алгоритмами;
-
работать с текстами научного стиля, составлять конспект;
-
осуществлять сравнение, самостоятельно выбирая основания и критерии для указанных логических операций;
-
формулировать собственное мнение и позицию, аргументировать и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности;
-
работать в группе - устанавливать рабочие отношения, эффективно сотрудничать и способствовать продуктивной кооперации;
Квадратичная функция y=ax2. Функция у=k/х.
Выпускник научится:
-
находить область определения и область значений функции, читать график функции;
-
строить графики функций у=ах2, функции у=k/х;
-
выполнять простейшие преобразования графиков функций;
-
строить график квадратичной функции,
-
находить по графику нули функции, промежутки, где функция принимает положительные и отрицательные значения;
-
решать квадратное уравнение графически;
-
решать неравенство ах2 +вх+с.≥0 на основе свойств квадратичной функции;
-
графически решать уравнения и системы уравнений;
-
графически определять число решений системы уравнений;
-
понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами;
-
упрощать функциональные выражения;
-
строить графики кусочно-заданных функций;
-
работать с чертёжными инструментами.
Выпускник получит возможность научиться:
-
проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.);
-
использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса;
-
строить графики с использованием возможностей специальных компьютерных инструментов и программ;
-
задавать вопросы, необходимые для организации собственной деятельности и сотрудничества с партнёром;
-
осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь;
-
на основе комбинирования ранее изученных алгоритмов и способов действия решать нетиповые задачи, выполняя продуктивные действия эвристического типа.
Функция у=х. Свойства квадратного корня.
Выпускник научится:
-
извлекать квадратный корень из неотрицательного числа;
-
строить график функции
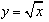 , описывать её свойства;
, описывать её свойства;
-
применять свойства квадратных корней при нахождении значения выражений;
-
решать квадратные уравнения, корнями которых являются иррациональные числа;
-
решать простейшие иррациональные уравнения;
-
выполнять упрощения выражений, содержащих квадратный корень с применением изученных свойств;
-
вычислять значения квадратных корней, не используя таблицу квадратов чисел
-
выполнять преобразования, содержащие операцию извлечения корня;
-
освобождаться от иррациональности в знаменателе;
-
раскладывать выражения на множители способом группировки, используя определение и свойства квадратного корня, формулы квадратов суммы и разности;
-
оценивать неизвлекаемые корни, находить их приближенные значения;
-
выполняют преобразования иррациональных выражений: сокращать дроби, раскладывая выражения на множители.
Выпускник получит возможность научиться:
-
свободно работать с текстами научного стиля;
-
делать умозаключения (индуктивное и по аналогии) и выводы на основе аргументации, формулировать выводы;
-
участвовать в диалоге, аргументированно отстаивать свою точку зрения;
-
понимать точку зрения собеседника, признавать право на иное мнение;
-
осуществлять проверку выводов, положений, закономерностей, теорем;
-
осуществлять контроль, коррекцию, оценку действий партнёра, уметь убеждать;
-
развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в практике.
Квадратные уравнения
Выпускник научится:
-
решать неполные квадратные уравнения;
-
решать квадратные уравнения выделением квадрата двучлена;
-
решать квадратные уравнения по формуле;
-
решать задачи с помощью квадратных уравнений;
-
применять теорему Виета и обратную теорему;
-
раскладывать на множители квадратный трёхчлен;
-
решать дробные рациональные уравнения;
-
решать задачи с помощью рациональных уравнений, выделяя три этапа математического моделирования;
-
решать рациональные уравнения, используя метод введения новой переменной;
-
решать биквадратные уравнения;
-
решать простейшие иррациональные уравнения.
Выпускник получит возможность научиться:
-
решать квадратные уравнения с параметрами и проводить исследование всех корней квадратного уравнения;
-
выполнять равносильные переходы при решении иррациональных уравнений разной степени трудности;
-
воспроизводить теорию с заданной степенью свернутости;
-
овладеть специальными приёмами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
-
применять графические представления для исследования уравнений, систем уравнений, содержащих параметр;
-
составлять план и последовательность действий в связи прогнозируемым результатом;
-
осуществлять контроль, коррекцию, оценку действий партнера.
Действительные числа
Выпускник научится:
-
округлять числа, записывать их в стандартном виде;
-
использовать начальные представления о множестве действительных чисел;
-
использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин;
-
упрощать выражения, используя определение степени с отрицательным показателем и свойства степени, выполнять преобразования выражений, содержащих степень с отрицательным показателем;
-
оперировать понятиями «тождество», «тождественное преобразование»; доказывать тождества.
Выпускник получит возможность научиться:
-
развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в практике;
-
развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби);
-
понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближёнными, что по записи приближённых значений, содержащихся в информационных источниках, можно судить о погрешности приближения;
-
понять, что погрешность результата вычислений должна быть соизмерима с погрешностью исходных данных;
-
самостоятельно задумывать, планировать и выполнять учебное исследование.
Неравенства
Выпускник научится:
-
решать неравенства с одной переменной и системы линейных неравенств с одной переменной;
-
решать квадратные неравенства методом интервалов;
-
применять свойства числовых неравенств;
-
исследовать различные функции на монотонность;
-
понимать и применять терминологию и символику, связанные с отношением неравенства, свойства числовых неравенств;
-
применять аппарат неравенств для решения задач.
Выпускник получит возможность научиться:
-
разнообразным приёмам доказательства неравенств; уверенно применять аппарат неравенств для решения разнообразных математических задач и задач из смежных предметов, практики;
-
применять графические представления для исследования неравенств, систем неравенств, содержащих буквенные коэффициенты (параметры);
-
использовать различные приёмы поиска информации в Интернете в ходе учебной деятельности;
-
аргументированно отвечать на поставленные вопросы;
-
объяснять изученные положения на самостоятельно подобранных конкретных примерах;
-
организовывать исследование с целью проверки гипотез;
-
осуществлять коммуникативную рефлексию как осознание оснований собственных действий и действий партнёра.
Информационно-методическое обеспечение
учебного процесса.
1. Дополнительные пособия для учителя.
1. Оценка качества подготовки выпускников основной школы по математике / Г. В. Дорофеев [и др.]. - М. : Дрофа, 2014.
2. Алгебра. 8 класс. Подготовка к итоговой аттестации : учебно-тренировочные тесты : в 2 ч. / под ред. Ф. Ф. Лысенко. - Ростов н/Д. : Легион, 2013.
3. Лебединцева, Е. А. Алгебра. 8 класс : задания для обучения и развития учащихся / Е. А. Лебединцева, Е. Ю. Беленкова. - М. : Интеллект-Центр, 2012.
4. Худадатова, С. С. Математика в ребусах, кроссвордах, чайнвордах, криптограммах. 8 класс / С. С. Худадатова. - М. : Школьная Пресса, 2014.
При работе можно использовать также статьи из научно-теоретического и методического журнала «Математика в школе», из еженедельного учебно-методического приложения к газете «Первое сентября» «Математика».
2. Дополнительные пособия для учащихся.
1. Звавич, Л. И. Задания по математике для подготовки к письменному экзамену в 9 классе / Л. И. Звавич [и др.]. - М. : Просвещение, 2012.
2. Пичурин, Л. Ф. За страницами учебника алгебры / Л. Ф. Пичурин. - М., 2013.
3. Дидактико-технологическое обеспечение учебного процесса.
Таблицы по курсу алгебры 8 класса.
Для информационно-компьютерной поддержки учебного процесса предполагается использование следующих программно-педагогических средств, реализуемых с помощью компьютера:
4. Программно-педагогические средства, реализуемые с помощью компьютера.
1. CD «1С: Репетитор. Математика» (КиМ).
2. CD «Алгебра не для отличников» (НИИ экономики авиационной промышленности).
3. CD «Математика. 5-11 классы. Практикум».
4. Видеоуроки Алгебра 8 класс.
Для обеспечения плодотворного учебного процесса предполагается использование информации и материалов следующих Интернет-ресурсов:
5. Интернет-ресурсы для учителя.
1. Министерство образования РФ. - Режим доступа : www.informika.ru; www.ed.gov.ru; www.edu.ru
2. Тестирование online: 5-11 классы. - Режим доступа : www.kokch.kts.ru/cdo
3. Педагогическая мастерская, уроки в Интернет и многое другое. - Режим доступа : teacher.fio.ru
4. Новые технологии в образовании. - Режим доступа : edu.secna.ru/main
5. Мегаэнциклопедия Кирилла и Мефодия. - Режим доступа : mega.km.ru
6. Сайты энциклопедий, например. - Режим доступа : www.rubricon.ru; www.ency-clopedia.ru
6. Цифровые образовательные ресурсы (ЦОР).
1. Интернет-портал Всероссийской олимпиады школьников. - Режим доступа : www. rusolymp.ru
2. Всероссийские дистанционные эвристические олимпиады по математике. - Режим доступа : www.eidos.ru/olymp/mathem/index.htm
3. Информационно-поисковая система «Задачи». - Режим доступа : zadachi.mccme.ru/ easy
4. Задачи: информационно-поисковая система задач по математике. - Режим доступа : zadachi.mccme.ru
5. Конкурсные задачи по математике: справочник и методы решения. - Режим доступа : mschool.kubsu.ru/cdo/shabitur/kniga/tit.htm
6. Материалы (полные тексты) свободно распространяемых книг по математике. - Режим доступа : www.mccme.ru/free-books
7. Математика для поступающих в вузы. - Режим доступа : www.matematika.agava.ru
8. Выпускные и вступительные экзамены по математике: варианты, методика. - Режим доступа : www.mathnet.spb.ru
9. Олимпиадные задачи по математике: база данных. - Режим доступа : zaba.ru
10/ Московские математические олимпиады. - Режим доступа : www.mccme.ru/olym-piads/mmo
11. Школьные и районные математические олимпиады в Новосибирске. - Режим доступа : aimakarov.chat.ru/school/school.html
12. Виртуальная школа юного математика. - Режим доступа : math.ournet.md/indexr.htm
13. Библиотека электронных учебных пособий по математике. - Режим доступа : mschool.kubsu.ru
14. Образовательный портал «Мир алгебры». - Режим доступа : www.algmir. org/ index.html
15. Словари БСЭ различных авторов. - Режим доступа : slovari.yandex.ru
16. Этюды, выполненные с использованием современной компьютерной 3D-графики, увлекательно и интересно рассказывающие о математике и ее приложениях. - Режим доступа : www.etudes.ru
17. Заочная физико-математическая школа. - Режим доступа : ido.tsu.ru/schools/physmat/ index.php
18. ЕГЭ по математике. - Режим доступа : uztest.ru
РАБОТА С ОДАРЕННЫМИ ДЕТЬМИ
На уроках проводится работа с одаренными детьми (дифференциация и индивидуализация в обучении):
- разноуровневые задания (задания более высокого уровня сложности);
- обучение самостоятельной работе (работа самостоятельно с учебником, с дополнительной литературой);
- творческие задания (составить задачу, выражение, кроссворд, ребус, анаграмму и т. д.)
КРИТЕРИИ И НОРМЫ ОЦЕНКИ ЗНАНИЙ, УМЕНИЙ И НАВЫКОВ ОБУЧАЮЩИХСЯ.
-
Критерии оценивания знаний, умений и навыков обучающихся по математике.
-
(Согласно Методическому письму «Направления работы учителей математики по исполнению единых требований преподавания предмета на современном этапе развития школы»)
-
Для оценки достижений учащихся применяется пятибалльная система оценивания.
-
Нормы оценки:
-
1. Оценка письменных контрольных работ обучающихся по математике.
-
Ответ оценивается отметкой «5», если:
-
1) работа выполнена полностью;
-
2) в логических рассуждениях и обосновании решения нет пробелов и ошибок;
-
3) в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
-
Отметка «4» ставится, если:
-
1) работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
-
2)допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
-
Отметка «3» ставится, если:
-
1) допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
-
Отметка «2» ставится, если:
-
1) допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
-
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
-
2.Оценка устных ответов обучающихся по математике
-
Ответ оценивается отметкой «5», если ученик:
-
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
-
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
-
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
-
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
-
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
-
отвечал самостоятельно, без наводящих вопросов учителя;
-
возможны одна - две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
-
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
-
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
-
допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
-
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
-
Отметка «3» ставится в следующих случаях:
-
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
-
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
-
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
-
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
-
Отметка «2» ставится в следующих случаях:
-
не раскрыто основное содержание учебного материала;
-
обнаружено незнание учеником большей или наиболее важной части учебного материала;
-
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Календарно-тематическое планирование.урока
Тема
Кол-во
часов
Дата
1-4
Повторение изученного в 7 классе (4 ч)
Глава 1. Алгебраические дроби (20 ч)
5
Основные понятия
1
6,7
Основное свойство алгебраической дроби.
2
8,9
Сложение и вычитание алгебраических дробей с одинаковыми знаменателями.
2
10-12
Сложение и вычитание алгебраических дробей с разными знаменателями.
3
13
Зачет № 1
1
14,15
Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень.
2
16-18
Преобразование алгебраических выражений.
3
19,20
Первые представления о решении рациональных уравнений (текстовые задачи).
2
21,22
Степень с отрицательным целым показателем.
2
23
Подготовка к контрольной работе.
1
24
Контрольная работа № 1.
1
Глава 11. Функция у=√х. Свойства квадратного корня. (18 ч)
25,26
Рациональные числа.
2
27,28
Понятие квадратного корня из неотрицательного числа.
2
29
Иррациональные числа.
1
30
Множество действительных чисел.
1
31
Функция у=√х, её свойства и график.
1
32
Зачет № 2.
1
33,34
Свойства квадратных корней.
2
35-37
Преобразование выражений, содержащих операцию извлечения квадратного корня.
3
38
Зачет № 3.
1
39-41
Модуль действительного числа, график функции у=|х|, формула √х2=|х|.
3
42
Контрольная работа № 2
1
Глава |||. Квадратичная функция. Функция у=к/х (16 ч)
43,44
Функция у=kx2, её свойства и график.
2
45,46
Функция у=к/х, её свойства и график.
2
47
Зачет № 4.
1
48,49
Как построить график функции у=f(x+l), если известен график функции у=f(x).
2
50,51
Как построить график функции у=f(x)+m, если известен график функции у=f(x).
2
52
Как построить график функции у=f(x+l)+m, если известен график функции у=f(x).
1
53
Зачет № 5
1
54-56
Функция у=ax2+bx+c, её свойства и график.
3
57
Графическое решение квадратных уравнений.
1
58
Контрольная работа № 3
1
Глава IV. Квадратные уравнения (20 ч)
59,60
Основные понятия.
2
61-63
Формулы корней квадратных уравнений.
3
64-66
Рациональные уравнения.
3
67-69
Рациональные уравнения как математические модели реальных ситуаций (текстовые задачи).
3
70
Контрольная работа № 4
1
71,72
Частные случаи формулы корней квадратного уравнения.
2
73,74
Теорема Виета. Разложение квадратного трехчлена на линейные множители.
2
75,76
Иррациональные уравнения.
2
77
Подготовка к контрольной работе.
1
78
Контрольная работа № 5.
1
Глава V. Неравенства (17 ч)
79-81
Свойства числовых неравенств.
3
82-84
Исследование функций на монотонность.
3
85,86
Решение линейных неравенств.
2
87,88
Решение квадратных неравенств.
2
89
Зачет № 6.
1
90-92
Приближенные значения действительных чисел., погрешность приближения, приближение по недостатку и избытку.
3
93
Стандартный вид положительного числа.
1
94
Подготовка к контрольной работе.
1
95
Контрольная работа № 6.
1
Итоговое повторение (10ч).
96-101
Итоговое повторение
6
102
Итоговая контрольная работа.
1
103-105
Итоговое повторение
3
КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ (8 КЛАСС)п/п
Тема урока(тип урока)
Основное содержание темы, термины и понятия
Вид контроля, измерители
Планируемые результаты
Универсальные учебные действия
Календарные сроки
Предметные
Личностные
Метапредметные
Познавательные УУД
Регулятивные УУД
Коммуникативные УУД
по плану
фактич
Повторение изученного в 7 классе (4 ч)
1
1
Повторение курса алгебры 7 класса (частично поисковый)
Свойства степени с натуральным показателем, действия со степенями одинакового показателя.
Взаимопроверка в парах. Работа с опорным материалом
Знают основные свойства степени с натуральным показателем. Умеют применять свойства при решении задач.
Готовность к выбору жизненного пути в соответствии с собственными интересами и возможностями.
Первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов.
Умеют выбирать смысловые единицы текста и устанавливать отношения между ними.
Определяют последовательность промежуточных целей с учетом конечного результата.
С достаточной полнотой и точностью выражают свои мысли в соответствии с задачами и условиями коммуникации.
2
2
Повторение курса алгебры 7 класса (Комбинированный)
Квадрат суммы, квадрат разности, разность квадратов, разность кубов, сумма кубов, разложение на множители по формулам сокращенного умножения.
Проблемные задания, фронтальный опрос, решение упражнения
Знают, как выполнять преобразования многочленов, применяя формулы сокращенного умножения: квадрат суммы и разности, разность квадратов, куб суммы и разности, сумма и разность кубов
Формирование познавательных интересов, интеллектуальных и творческих способностей учащихся.
Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни.
Выбирают знаково-символические средства для построения модели.
Сличают способ и результат своих действий с заданным эталоном, обнаруживают отклонения и отличия от эталона.
Понимают возможность различных точек зрения, не совпадающих с собственной.
3
3
Повторение курса алгебры 7 класса (Проблемное изложение)
Линейная функция, график линейной функции, взаимное расположение графиков линейных функций.
Практикум. Фронтальный опрос, упражнения
Могут строить графики линейных функций, описывать свойства функций.
Формирование познавательных интересов, интеллектуальных и творческих способностей учащихся.
Выделять основное содержание прочитанного текста, находить в нем ответы на поставленные вопросы и излагать его
Определяют основную и второстепенную информацию.
Принимают познавательную цель, сохраняют ее при выполнении учебных действий, регулируют весь процесс их выполнения и четко выполняют требования познавательной задачи.
Адекватно используют речевые средства для дискуссии и аргументации своей позиции.
4
4
Повторение курса алгебры 7 класса (Комбинированный)
Метод подстановки, метод алгебраического сложения, система двух линейных уравнений с двумя переменными.
Работа с опорными конспектами, работа с раздаточным материалом
Умеют решать системы двух линейных уравнений с двумя переменными методом подстановки
Готовность к выбору жизненного пути в соответствии с собственными интересами и возможностями.
Умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме;
Выбирают наиболее эффективные способы решения задачи в зависимости от конкретных условий.
Предвосхищают временные характеристики достижения результата (когда будет результат?).
Интересуются чужим мнением и высказывают свое.
Глава 1. Алгебраические дроби (20 ч)
5
1
Основные понятия
Алгебраическая дробь, числитель дроби, знаменатель дроби, область допустимых значений, основное свойство дроби
Имеют представление о числителе, знаменателе алгебраической дроби, о значении алгебраической дроби и о значении переменной, при которой алгебраическая дробь не имеет смысла
Взаимопроверка в парах. Работа с опорным материалом
Проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности
Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
Сличают свой способ действия с эталоном
Ориентируются и воспринимают тексты научного и публицистического стилей
Описывают содержание совершаемых действий с целью ориентировки деятельности
Работа с книгой, конспектом и наглядными пособиями по группам.
6
2
Основное свойство алгебраической дроби.
основное свойство дроби
Знать основное свойство дроби
Выдвигают и обосновывают гипотезы, предлагают способы их проверки.
Сличают свой способ действия с эталоном.
Используют адекватные языковые средства для отображения своих чувств, мыслей и побуждений.
7
3
Основное свойство алгебраической дроби.
Основное свойство дроби. Сокращение дробей
Уметь формулировать основное свойство дроби и применять его для преобразования дробей
Выбирают наиболее эффективные способы решения задачи в зависимости от конкретных условий.
Сличают способ и результат своих действий с заданным эталоном, обнаруживают отклонения и отличия от эталона.
Проявляют готовность адекватно реагировать на нужды других, оказывать помощь и эмоциональную поддержку партнерам. Проявляют готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции.
8
4
Сложение и вычитание алгебраических дробей с одинаковыми знаменателями.
Сложение и вычитание дробей с одинаковым знаменателем
Практикум. Решение качественных задач
Умеют применять основное свойство дроби при преобразовании алгебраических дробей и их сокращении; находить значение дроби при заданном значении переменной.
Объясняют самому себе свои наиболее заметные достижения, дают адекватную оценку результатам своей учебной деятельности, проявляют познавательный интерес к изучению предмета
Первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
Самостоятельно формулируют познавательную цель
Выделяют обобщенный смысл и формальную структуру задачи
Умеют (или развивают способность) брать на себя инициативу в организации совместного действия
9
5
Сложение и вычитание алгебраических дробей с одинаковыми знаменателями.
Сложение и вычитание дробей с одинаковым знаменателем
Работа с конспектом, с книгой и наглядными пособиями по группам
Умеют применять основное свойство дроби при преобразовании алгебраических дробей и их сокращении; находить значение дроби при заданном значении переменной.
Объясняют самому себе свои наиболее заметные достижения, дают адекватную оценку результатам своей учебной деятельности, проявляют познавательный интерес к изучению предмета
Первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
Выделяют обобщенный смысл и формальную структуру задачи.
Осознают качество и уровень усвоения.
Умеют слушать и слышать друг друга. Учатся устанавливать и сравнивать разные точки зрения, прежде чем принимать решение и делать выбор. Устанавливают рабочие отношения, учатся эффективно сотрудничать и способствовать продуктивной кооперации. Проявляют готовность адекватно реагировать на нужды других, оказывать помощь и эмоциональную поддержку партнерам.
10
6
Сложение и вычитание алгебраических дробей с разными знаменателями.
Нахождение общего знаменателя дробей. Знать формулы сокращенного умножения и уметь их применять
Практикум. Решение качественных задач
Умеют применять основное свойство дроби при преобразовании алгебраических дробей и их сокращении; находить значение дроби при заданном значении переменной.
Объясняют самому себе свои наиболее заметные достижения, дают адекватную оценку результатам своей учебной деятельности, проявляют познавательный интерес к изучению предмета
Первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
Самостоятельно формулируют познавательную цель
Выделяют обобщенный смысл и формальную структуру задачи
Умеют (или развивают способность) брать на себя инициативу в организации совместного действия
11
7
Сложение и вычитание алгебраических дробей с разными знаменателями.
Упрощение выражений, сложение и вычитание алгебраических дробей с разными знаменателями, наименьший общий знаменатель, правило приведения алгебраических дробей к общему знаменателю, дополнительный множитель, допустимые значения переменных
Работа с конспектом, с книгой и наглядными пособиями по группам
Имеют представление о наименьшем общем знаменателе, о дополнительном множителе, о выполнении действия сложения и вычитания дробей с разными знаменателями.
Объясняют отличия в оценках одной и той же ситуации разными людьми, проявляют положительное отношение к урокам математики, дают положительную оценку и самооценку результатов учебной деятельности
Умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
Сличают свой способ действия с эталоном
Анализируют условия и требования задачи
Обмениваются знаниями между членами группы для принятия совместных решений
12
8
Сложение и вычитание алгебраических дробей с разными знаменателями.
Упрощение выражений, сложение и вычитание алгебраических дробей с разными знаменателями, наименьший общий знаменатель, правило приведения алгебраических дробей к общему знаменателю, дополнительный множитель, допустимые значения переменных
Проблемные задания. Взаимопроверка в парах. Решение упражнения
Умеют находить общий знаменатель нескольких дробей. Знают алгоритм сложения и вычитания дробей с разными знаменателями.
Объясняют самому себе свои наиболее заметные достижения, проявляют познавательный интерес к изучению предмета, дают адекватную оценку результатам своей учебной деятельности, принимают и осознают социальную роль ученика
Умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
Вносят коррективы и дополнения в способ своих действий
Выражают смысл ситуации различными средствами (рисунки, символы, схемы, знаки)
Придерживаются морально-этических и психологических принципов сотрудничества
13
9
Зачет № 1
Упрощение выражений, сложение и вычитание алгебраических дробей с разными знаменателями, наименьший общий знаменатель, правило приведения алгебраических дробей к общему знаменателю, дополнительный множитель, допустимые значения переменных
Фронтальный опрос. Выборочный диктант. Решение качественных задач
Умеют находить общий знаменатель нескольких дробей; упрощать выражения, применяя формулы сокращенного умножения, доказывать тождества
Объясняют отличия в оценках одной и той же ситуации разными людьми, дают адекватную оценку результатам своей учебной деятельности, проявляют интерес к предмету
Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
Составляют план и последовательность действий
Выбирают знаково-символические средства для построения модели
Общаются и взаимодействуют с партнерами по совместной деятельности или обмену информацией
14
10
Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень.
Умножение и деление алгебраических дробей, возведение алгебраических дробей в степень, преобразование выражений, содержащих алгебраические дроби
Проблемные задания, фронтальный опрос, упражнения
Имеют представление об умножении и делении алгебраических дробей, возведении их в степень.
Проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности, проявляют познавательный интерес к изучению предмета, понимают причины успеха в учебной деятельности
Формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности
Самостоятельно формулируют познавательную цель и строят действия в соответствии с ней
Структурируют знания. Осознанно и произвольно строят речевые высказывания
Учатся контролировать, корректировать и оценивать действия партнера
15
11
Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень.
Умножение и деление алгебраических дробей, возведение алгебраических дробей в степень, преобразование выражений, содержащих алгебраические дроби
Практикум. Фронтальный опрос, упражнения
Умеют пользоваться алгоритмами умножения и деления дробей, возведения дроби в степень, упрощая выражения
Объясняют самому себе свои отдельные ближайшие цели саморазвития, понимают и осознают социальную роль ученика, дают адекватную самооценку результатам учебной деятельности, понимают причины успеха в учебной деятельности
Умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
Вносят коррективы и дополнения в способ своих действий
Умеют выводить следствия из имеющихся в условии задачи данных
Умеют слушать и слышать друг друга. Адекватно используют речевые средства
16
12
Преобразование алгебраических выражений.
Преобразование рациональных выражений, рациональные выражения, доказательство тождества
Фронтальный опрос. Работа с демонстрационным материалом
Имеют представление о преобразовании рациональных выражений, используя все действия с алгебраическими дробями.
Проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности, проявляют интерес к предмету
Формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
Самостоятельно формулируют познавательную цель и строят действия в соответствии с ней
Проводят анализ способов решения задач
Умеют представлять конкретное содержание и сообщать его в письменной и устной форме
17
13
Преобразование алгебраических выражений.
Преобразование рациональных выражений, рациональные выражения, доказательство тождества
Построение алгоритма действия, решение упражнений
Знают, как преобразовывают рациональные выражения, используя все действия с алгебраическими дробями
Объясняют самому себе свои наиболее заметные достижения, понимают причины успеха в учебной деятельности, проявляют познавательный интерес к изучению предмета, дают оценку и самооценку результатов учебной деятельности
Формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности
Сличают свой способ действия с эталоном
Выбирают наиболее эффективные способы решения задачи в зависимости от конкретных условий
Учатся организовывать и планировать учебное сотрудничество с учителем и сверстниками
18
14
Преобразование алгебраических выражений.
Преобразование рациональных выражений, рациональные выражения, доказательство тождества
Работа с опорными конспектами, работа с раздаточным материалом
Могут преобразовывать рациональные выражения, используя все действия с алгебраическими дробями.
Проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности
Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению
Анализируют объект, выделяя существенные и несущественные признаки
Работают в группе. Устанавливают рабочие отношения, учатся эффективно сотрудничать
19
15
Первые представления о решении рациональных уравнений (текстовые задачи).
Рациональные уравнения
Построение алгоритма действия, решение упражнений
Знают, как преобразовывают рациональные выражения, используя все действия с алгебраическими дробями
Объясняют самому себе свои наиболее заметные достижения, понимают причины успеха в учебной деятельности, проявляют познавательный интерес к изучению предмета, дают оценку и самооценку результатов учебной деятельности
Формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности
Сличают свой способ действия с эталоном
Выбирают наиболее эффективные способы решения задачи в зависимости от конкретных условий
Учатся организовывать и планировать учебное сотрудничество с учителем и сверстниками
20
16
Первые представления о решении рациональных уравнений (текстовые задачи).
Рациональные уравнения
Построение алгоритма действия, решение упражнений
Могут преобразовывать рациональные выражения, используя все действия с алгебраическими дробями.
Проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности
Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению
Анализируют объект, выделяя существенные и несущественные признаки
Работают в группе. Устанавливают рабочие отношения, учатся эффективно сотрудничать
21
17
Степень с отрицательным целым показателем.
Степень с отрицательным показателем, тождества степеней, свойства степени с рациональным показателем, стандартный вид числа, степень с нулевым показателем.
Построение алгоритма решения задания
Имеют представление о степени с отрицательным целым и нулевым показателем.
Готовность к выбору жизненного пути в соответствии с собственными интересами и возможностями.
Овладение навыками самостоятельного приобретения новых знаний.
Структурируют знания.
Оценивают достигнутый результат.
Учатся разрешать конфликты - выявлять, идентифицировать проблемы, искать и оценивать альтернативные способы разрешения конфликта, принимать решение и реализовывать его.
22
18
Степень с отрицательным целым показателем.
Степень с отрицательным показателем, тождества степеней, свойства степени с рациональным показателем, стандартный вид числа, степень с нулевым показателем.
Проблемные задания, ответы на вопросы
Могут вычислить степень с рациональным показателем, применяя все свойства; рассуждать, обобщать, видеть несколько решений одной задачи
Развитие интереса к математическому творчеству и математических способностей.
Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера
Осознанно и произвольно строят речевые высказывания в устной и письменной форме.
Вносят коррективы и дополнения в составленные планы.
Вступают в диалог, участвуют в коллективном обсуждении проблем, учатся владеть монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка.
23
19
Подготовка к контрольной работе.
Степень с отрицательным показателем, тождества степеней, свойства степени с рациональным показателем, стандартный вид числа, степень с нулевым показателем. Рациональные уравнения
Работа с опорными конспектами, работа с раздаточным материалом
Могут преобразовывать рациональные выражения, используя все действия с алгебраическими дробями. Могут вычислить степень с рациональным показателем, применяя все свойства; рассуждать, обобщать, видеть несколько решений одной задачи
Проявляют устойчивый и широкий интерес к способам решения познавательных задач, адекватно оценивают результаты своей учебной деятельности Развитие интереса к математическому творчеству и математических способностей.
Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем; Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера
Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению
Анализируют объект, выделяя существенные и несущественные признаки
Работают в группе. Устанавливают рабочие отношения, учатся эффективно сотрудничать
24
20
Контрольная работа № 1.
Степень с отрицательным показателем, тождества степеней, свойства степени с рациональным показателем, стандартный вид числа, степень с нулевым показателем. Рациональные уравнения
Индивидуальное решение контрольных заданий
Демонстрируют умение обобщения и систематизации знаний по темам раздела «Алгебраические дроби».
Объясняют самому себе свои наиболее заметные достижения, проявляют познавательный интерес к изучению предмета, дают адекватную оценку и самооценку деятельности
Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
Предвосхищают результат и уровень усвоения (какой будет результат?)
Выбирают наиболее эффективные способы решения задачи в зависимости от конкретных условий
Умеют представлять конкретное содержание и сообщать его в письменной форме
Глава 11. Функция у=√х. Свойства квадратного корня. (18 ч)
25
1
Рациональные числа.
Натуральные числа. Целые числа. Множество рациональных чисел, знак принадлежности, знак включения, символы математического языка, бесконечные десятичные периодические дроби, период, чисто периодическая дробь, смешано периодическая дробь
Проблемные задания, ответы на вопросы
Знать понятие рационального числа, бесконечной десятичной периодической дроби
Развитие интереса к математическому творчеству и математических способностей.
Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера
Выполняют операции со знаками и символами.
Ставят учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что еще неизвестно.
Умеют слушать и слышать друг друга.
26
2
Рациональные числа.
Рациональные числа. Множество рациональных чисел, знак принадлежности, знак включения, символы математического языка, бесконечные десятичные периодические дроби, период, чисто периодическая дробь, смешано периодическая дробь
Работа с опорными конспектами, работа с раздаточным материалом
Знать понятие рационального числа, бесконечной десятичной периодической дроби.
Готовность к выбору жизненного пути в соответствии с собственными интересами и возможностями.
Овладение навыками самостоятельного приобретения новых знаний.
Выделяют и формулируют познавательную цель.
Принимают познавательную цель, сохраняют ее при выполнении учебных действий, регулируют весь процесс их выполнения и четко выполняют требования познавательной задачи.
Учатся управлять поведением партнера - убеждать его, контролировать, корректировать и оценивать его действия.
27
3
Понятие квадратного корня из неотрицательного числа.
Квадратный корень, квадратный корень из неотрицательного числа, подкоренное выражение, извлечение квадратного корня, иррациональные числа, кубический корень из неотрицательного числа.
Индивидуальный опрос. Выполнение упражнений по образцу
Имеют представление, как извлекать квадратные корни из неотрицательного числа. Знают действительные и иррациональные числа.
Формирование познавательных интересов, интеллектуальных и творческих способностей учащихся.
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Составляют целое из частей, самостоятельно достраивая, восполняя недостающие компоненты.
Сличают свой способ действия с эталоном.
Демонстрируют способность к эмпатии, стремление устанавливать доверительные отношения взаимопонимания.
28
4
Понятие квадратного корня из неотрицательного числа.
Квадратный корень, квадратный корень из неотрицательного числа, подкоренное выражение, извлечение квадратного корня, иррациональные числа, кубический корень из неотрицательного числа.
Индивидуальный опрос. Выполнение упражнений по образцу
Имеют представление, как извлекать квадратные корни из неотрицательного числа. Знают действительные и иррациональные числа.
Формирование познавательных интересов, интеллектуальных и творческих способностей учащихся.
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Составляют целое из частей, самостоятельно достраивая, восполняя недостающие компоненты.
Сличают свой способ действия с эталоном.
Демонстрируют способность к эмпатии, стремление устанавливать доверительные отношения взаимопонимания.
29
5
Иррациональные числа.
Иррациональные числа, бесконечные десятичная непериодическая дробь, иррациональные выражения.
Разноуровневые задания
Знают определение иррационального числа. Иррациональность числа и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел.
Готовность к выбору жизненного пути в соответствии с собственными интересами и возможностями.
Овладение навыками самостоятельного приобретения новых знаний.
Умеют описывать множество целых чисел. Приводить примеры иррациональных чисел распознавать иррациональные числа,, изображать числа точками координатной прямой.
Освоение социальных норм, правил поведения, ролей и форм социальной жизни в группах и сообществах.
Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем
30
6
Множество действительных чисел.
Числовые промежутки, интервал, отрезок, луч..
Индивидуальный опрос. Выполнение упражнений по образцу
Знают определение действительных чисел. Сравнивать и упорядочивать действительные числа.
Мотивация образовательной деятельности школьников на основе личностно ориентированного подхода.
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Выбирают основания и критерии для сравнения, сериации, классификации объектов.
Определяют последовательность промежуточных целей с учетом конечного результата
Учатся переводить конфликтную ситуацию в логический план и разрешать ее как задачу через анализ условий.
31
7
Функция у=√х, её свойства и график.
Функция у=√x, ее свойства и график, функция, выпуклая вверх, функция, выпуклая вниз.
Проблемные задания.Разноуровневые задания
Знают определение функции, область определения и область значений функции., способы задания функции. Умеют выполнять построение графика функции. Свойства функции
Развитие морального сознания и компетентности в решении моральных проблем на основе личностного выбора.
Понимать сущности алгометрических предписаний и умение действовать в соответствии с предложенным алгоритмом. Использовать математические средства наглядности графики для интерпритации, аргументации.
Составляют целое из частей, самостоятельно достраивая, восполняя недостающие компоненты.
Сличают свой способ действия с эталоном.
Демонстрируют способность к эмпатии, стремление устанавливать доверительные отношения взаимопонимания.
32
8
Зачет № 2.
Множество действительных чисел, сравнение действительных чисел, действия над действительными числами. Функция у=√x, ее свойства и график, функция, выпуклая вверх, функция, выпуклая вниз.
Фронтальный опрос. Выборочный диктант. Решение качественных задач
Знают понятие: рациональные числа, бесконечная десятичная периодическая дробь; иррациональное число. Могут любое рациональное число записать в виде конечной десятичной дроби и наоборот. Знают определение функции, область определения и область значений функции., способы задания функции. Умеют выполнять построение графика функции. Свойства функции
Объясняют отличия в оценках одной и той же ситуации разными людьми, дают адекватную оценку результатам своей учебной деятельности, проявляют интерес к предмету
Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
Составляют план и последовательность действий
Выбирают знаково-символические средства для построения модели
Общаются и взаимодействуют с партнерами по совместной деятельности или обмену информацией
33
9
Свойства квадратных корней.
Квадратный корень из произведения, квадратный корень из дроби, вычисление корней.
Проблемные задания..Разноуровневые задания
Знают определение квадратного корня, свойства квадратных корней. Умеют применять свойства при преобразовнии и упрощении выражений.
Умение осуществлять и планировать деятельность, направленную на решение задач исследовательского характера
Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем
Выбирают основания и критерии для сравнения, сериации, классификации объектов.
Определяют последовательность промежуточных целей с учетом конечного результата
Учатся переводить конфликтную ситуацию в логический план и разрешать ее как задачу через анализ условий.
34
10
Свойства квадратных корней.
Квадратный корень из произведения, квадратный корень из дроби, вычисление корней.
Фронтальный опрос. Выборочный диктант. Решение качественных задач
Доказывать свойства арифметических квадратных корней, применяя их для преобразования выражений. Вычислять значение выражений, содержащих квадратные корни, выражать переменные из геометрических и физических формул
Знают определение квадратного корня, свойства квадратных корней. Умеют применять свойства при преобразовнии и упрощении выражений.
Умение осуществлять и планировать деятельность, направленную на решение задач исследовательского характера
Составляют план и последовательность действий
Выбирают знаково-символические средства для построения модели
Общаются и взаимодействуют с партнерами по совместной деятельности или обмену информацией
35
11
Преобразование выражений, содержащих операцию извлечения квадратного корня.
Дествия с выражениями, содержащими квадратные корни
Работа с конспектом, с книгой и наглядными пособиями по группам
Иметь представление о преобразовании выражений, об извлечении квадратного корня и освобождении иррациональности в знаменателе.
Мотивация образовательной деятельности школьников на основе личностно ориентированного подхода.
Умение принимать решение в условиях неполной и избыточной, точной и вероятностной информации
Выбирают знаково-символические средства для построения модели.
Предвосхищают результат и уровень усвоения (какой будет результат?).
Понимают возможность различных точек зрения, не совпадающих с собственной.
36
12
Преобразование выражений, содержащих операцию извлечения квадратного корня.
Дествия с выражениями, содержащими квадратные корни
Фронтальный опрос. Решение качественных задач
Знать о преобразовании выражений, об операциях извлечения квадратного корня и освобождении иррациональности в знаменателе.
Мотивация образовательной деятельности школьников на основе личностно ориентированного подхода.
Умение принимать решение в условиях неполной и избыточной, точной и вероятностной информации
Выбирают знаково-символические средства для построения модели.
Предвосхищают результат и уровень усвоения (какой будет результат?).
Понимают возможность различных точек зрения, не совпадающих с собственной.
37
13
Преобразование выражений, содержащих операцию извлечения квадратного корня.
Дествия с выражениями, содержащими квадратные корни
Фронтальный опрос. Решение качественных задач
Уметь выполнять преобразования, содержащие операцию извлечения корня, освобождаться лот иррациональности в знаменателе.
Мотивация образовательной деятельности школьников на основе личностно ориентированного подхода.
Умение принимать решение в условиях неполной и избыточной, точной и вероятностной информации
Выбирают знаково-символические средства для построения модели.
Предвосхищают результат и уровень усвоения (какой будет результат?).
Понимают возможность различных точек зрения, не совпадающих с собственной.
38
14
Зачет № 3.
Понятие квадратного корня, арифметического квадратного корня.
Фронтальный опрос. Выборочный диктант. Решение качественных задач
Знают определение квадратного корня, свойства квадратных корней. Умеют применять свойства при преобразовании и упрощении выражений
Объясняют отличия в оценках одной и той же ситуации разными людьми, дают адекватную оценку результатам своей учебной деятельности, проявляют интерес к предмету
Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
Составляют план и последовательность действий
Выбирают знаково-символические средства для построения модели
Общаются и взаимодействуют с партнерами по совместной деятельности или обмену информацией
39
15
Модуль действительного числа, график функции у=|х|, формула √х2=|х|.
Модуль действительного числа, свойства модулей, геометрический смысл модуля действительного числа, совокупность уравнений, тождество √a2=|a|.
Решение проблемных задач
Могут решать модульные уравнения, неравенства и вычислять примеры на все действия с модулями.
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту
Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
Осуществляют поиск и выделение необходимой информации
Ставят учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что еще неизвестно.
Учатся разрешать конфликты - выявлять, идентифицировать проблемы, искать и оценивать альтернативные способы разрешения конфликта, принимать решение и реализовывать его.
40
16
Модуль действительного числа, график функции у=|х|, формула √х2=|х|.
Расстояние меду точками координатной прямой, противоположные точки, противоположные числа, целые числа, рациональные числа, модуль числа.
Работа с опорными конспектами, работа с раздаточным материалом
Знают как строить графики функций. Умеют упрощать функциональные выражен ия,строить графики кусочно-заданных функций
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту
Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.
Умеют выбирать обобщенные стратегии решения задачи
Вносят коррективы и дополнения в способ своих действий в случае расхождения эталона, реального действия и его продукта.
Учатся аргументировать свою точку зрения, спорить и отстаивать свою позицию невраждебным для оппонентов образом.
41
17
Модуль действительного числа, график функции у=|х|, формула √х2=|х|.
Расстояние меду точками координатной прямой, противоположные точки, противоположные числа, целые числа, рациональные числа, модуль числа.
Решение проблемных задач
Могут решать модульные уравнения, неравенства и вычислять примеры на все действия с модулями.
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту
Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.
Умеют выбирать обобщенные стратегии решения задачи
Вносят коррективы и дополнения в способ своих действий в случае расхождения эталона, реального действия и его продукта.
Учатся аргументировать свою точку зрения, спорить и отстаивать свою позицию невраждебным для оппонентов образом.
42
18
Контрольная работа № 2
Индивидуальное решение контрольных заданий
Демонстрируют умение обобщения и систематизации знаний по основным темам раздела «Функция у=√х. Свойства квадратного корня.».
Умение контролировать процесс и результат учебной математической деятельности.
Овладение навыками самоконтроля и оценки результатов своей деятельности, умениями предвидеть возможные результаты своих действий.
Осознанно и произвольно строят речевые высказывания в письменной форме.
Осознают качество и уровень усвоения.
Проявляют готовность адекватно реагировать на нужды других, оказывать помощь и эмоциональную поддержку партнерам.
Глава |||. Квадратичная функция. Функция у=к/х (16 ч)
43
1
Функция у=kx2, её свойства и график.
Кусочно-заданные функции, контрольные точки графика, парабола, вершина параболы, ось симметрии параболы, фокус параболы, функция y= kx2 , график функции y= kx2.
Практикум. Фронтальный опрос. Математический диктант
Имеют представления о функции вида у = кх2, о ее графике и свойствах.
Критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта.
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Создают структуру взаимосвязей смысловых единиц текста.
Предвосхищают временные характеристики достижения результата (когда будет результат?).
Понимают возможность различных точек зрения, не совпадающих с собственной.
44
2
Функция у=kx2, её свойства и график.
Кусочно-заданные функции, контрольные точки графика, парабола, вершина параболы, ось симметрии параболы, фокус параболы, функция y= kx2 , график функции y= kx2.
Работа с опорными конспектами, работа с раздаточным материалом
Умеют строить график функции у = кх2
Знают как строить графики функций. Умеют упрощать функциональные выражен ия,строить графики кусочно-заданных функций..
.Умеют упрощать функциональные выражения, строить графики кусочно-заданных функций
Самостоятельность в приобретении новых знаний и практических умений.
Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем.
Выделяют количественные характеристики объектов, заданные словами.
Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению, осознают качество и уровень усвоения.
Умеют представлять конкретное содержание и сообщать его в письменной и устной форме.
45
3
Функция у=к/х, её свойства и график
Функция у=1/x. Гипербола, ветви гиперболы, асимптоты, ось симметрии гиперболы. Функция у=к/х, обратная пропорциональность, коэффициент обратной пропорциональности, свойства функции у=к/х, область значений функции, окрестность точки, точка максимума, точка минимума.
Фронтальный опрос. Решение качественых задач
Имеют представления о функции вида у = k/x, о ее графике и свойствах.
Способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации
Умеют выводить следствия из имеющихся в условии задачи данных
Вносят коррективы и дополнения в способ своих действий в случае расхождения эталона, реального действия и его продукта.
Интересуются чужим мнением и высказывают свое.
46
4
Функция у=к/х, её свойства и график
Функция у=1/x. Гипербола, ветви гиперболы, асимптоты, ось симметрии гиперболы. Функция у=к/х, обратная пропорциональность, коэффициент обратной пропорциональности, свойства функции у=к/х, область значений функции, окрестность точки, точка максимума, точка минимума.
Построение алгоритма действия, решение упражнений
Могут упрощать функциональные выражения, строить графики кусочно-заданных функций
Креативность мышления, инициатива, находчивость, активность при решении математических задач.
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Выделяют формальную структуру задачи.
Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению, осознают качество и уровень усвоения.
Развивают умение интегрироваться в группу сверстников и строить продуктивное взаимодействие со сверстниками и взрослыми.
47
5
Зачет № 4.
Квадратичная функция. Функция у=к/х
Фронтальный опрос. Выборочный диктант. Решение качественных задач
Уметь обобщать и систематизировать знания и умения по данной теме.
Объясняют отличия в оценках одной и той же ситуации разными людьми, дают адекватную оценку результатам своей учебной деятельности, проявляют интерес к предмету
Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
Составляют план и последовательность действий
Выбирают знаково-символические средства для построения модели
Общаются и взаимодействуют с партнерами по совместной деятельности или обмену информацией
48
6
Как построить график функции у=f(x+l), если известен график функции у=f(x).
Параллельный перенос, параллельные перенос вправо (влево), вспомогательная система координат, алгоритм построения графика функции y=f(x+l).
Построение алгоритма действия, решение упражнений
Иметь представление как с помощью параллельного переноса вправо и влево построить график функции y=f(x+l).
Креативность мышления, инициатива, находчивость, активность при решении математических задач.
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Выделяют формальную структуру задачи.
Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению, осознают качество и уровень усвоения.
Развивают умение интегрироваться в группу сверстников и строить продуктивное взаимодействие со сверстниками и взрослыми.
49
7
Как построить график функции у=f(x+l), если известен график функции у=f(x).
Параллельный перенос, параллельные перенос вправо (влево), вспомогательная система координат, алгоритм построения графика функции y=f(x+l).
Фронтальный опрос. Решение качественых задач
Иметь представление как с помощью параллельного переноса вправо и влево построить график функции y=f(x+l).
Способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации
Умеют выводить следствия из имеющихся в условии задачи данных
Вносят коррективы и дополнения в способ своих действий в случае расхождения эталона, реального действия и его продукта.
Интересуются чужим мнением и высказывают свое.
50
8
Как построить график функции у=f(x)+m, если известен график функции у=f(x).
Параллельный перенос, параллельный перенос вверх (вниз), вспомогательная система координат, алгоритм построения графика функции у = f(x) + т.
Построение алгоритма действия, решение упражнений
Иметь представление, как с помощью параллельного переноса вверх или вниз построить график функции у = f(x) + т.
Креативность мышления, инициатива, находчивость, активность при решении математических задач.
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Выделяют формальную структуру задачи.
Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению, осознают качество и уровень усвоения.
Развивают умение интегрироваться в группу сверстников и строить продуктивное взаимодействие со сверстниками и взрослыми.
51
9
Как построить график функции у=f(x)+m, если известен график функции у=f(x).
Параллельный перенос, параллельный перенос вверх (вниз), вспомогательная система координат, алгоритм построения графика функции у = f(x) + т.
Фронтальный опрос. Решение качественых задач
Иметь представление, как с помощью параллельного переноса вверх или вниз построить график функции у = f(x) + т.
Способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации
Умеют выводить следствия из имеющихся в условии задачи данных
Вносят коррективы и дополнения в способ своих действий в случае расхождения эталона, реального действия и его продукта.
Интересуются чужим мнением и высказывают свое.
52
10
Как построить график функции у=f(x+l)+m, если известен график функции у=f(x).
Параллельный перенос, вспомогательная система координат, алгоритм построения графика функции у = f(x + l) + т.
Построение алгоритма действия, решение упражнений
Иметь представление, как с помощью параллельного переноса построить график функции у = f(x + l) + т.
Креативность мышления, инициатива, находчивость, активность при решении математических задач.
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Выделяют формальную структуру задачи.
Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению, осознают качество и уровень усвоения.
Развивают умение интегрироваться в группу сверстников и строить продуктивное взаимодействие со сверстниками и взрослыми.
53
11
Зачет № 5
Параллельный перенос, вспомогательная система координат, алгоритм построения графика функции у = f(x + l) + т.
Фронтальный опрос. Выборочный диктант. Решение качественных задач
Уметь обобщать и систематизировать знания и умения по данной теме.
Объясняют отличия в оценках одной и той же ситуации разными людьми, дают адекватную оценку результатам своей учебной деятельности, проявляют интерес к предмету
Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
Составляют план и последовательность действий
Выбирают знаково-символические средства для построения модели
Общаются и взаимодействуют с партнерами по совместной деятельности или обмену информацией
54
12
Функция у=ax2+bx+c, её свойства и график.
Функция у = ах2 + вх + с, квадратичная функция, график квадратичной функции, ось параболы, формула абсциссы параболы, направление веток параболы, алгоритм построения параболы у = ах2 +вх + с.
Фронтальный опрос. Решение качественных задач
Имеют представление о функции у = ах2 + вх + с, о ее графике и свойствах
Формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта
Умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки.
Восстанавливают предметную ситуацию, описанную в задаче, путем переформулирования, упрощенного пересказа текста, с выделением только существенной для решения задачи информации.
Вносят коррективы и дополнения в составленные планы.
Адекватно используют речевые средства для дискуссии и аргументации своей позиции.
55
13
Функция у=ax2+bx+c, её свойства и график.
Функция у = ах2 + вх + с, квадратичная функция, график квадратичной функции, ось параболы, формула абсциссы параболы, направление веток параболы, алгоритм построения параболы у = ах2 +вх + с.
Фронтальный опрос. Решение качественных задач
Имеют представление о функции у = ах2 + вх + с, о ее графике и свойствах
Формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта
Умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки.
Восстанавливают предметную ситуацию, описанную в задаче, путем переформулирования, упрощенного пересказа текста, с выделением только существенной для решения задачи информации.
Вносят коррективы и дополнения в составленные планы.
Адекватно используют речевые средства для дискуссии и аргументации своей позиции.
56
14
Функция у=ax2+bx+c, её свойства и график.
Функция у = ах2 + вх + с, квадратичная функция, график квадратичной функции, ось параболы, формула абсциссы параболы, направление веток параболы, алгоритм построения параболы у = ах2 +вх + с.
Построение алгоритма действия, решение упражнений
Могут строить график функции у = ах2 + вх + с, описывать свойства по графику.
Воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения
Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем.
Выделяют обобщенный смысл и формальную структуру задачи.
Сличают свой способ действия с эталоном
Планируют общие способы работы.
\57
15
Графическое решение квадратных уравнений.
Квадратное уравнение, несколько способов графического решения уравнения
Практикум. Фронтальный опрос. Работа с раздаточными материалами
Могут строить график функции у = ах2 + вх + с, описывать свойства по графику. Могут решать квадратные уравнения графическим методом.
Умение контролировать процесс и результат учебной математической деятельности
Умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации
Умеют выводить следствия из имеющихся в условии задачи данных.
Оценивают достигнутый результат.
Устанавливают рабочие отношения, учатся эффективно сотрудничать и способствовать продуктивной кооперации.
58
16
Контрольная работа № 3
Функция у = ах2 + вх + с, квадратичная функция, график квадратичной функции, ось параболы, формула абсциссы параболы, направление веток параболы, алгоритм построения параболы у = ах2 +вх + с.
Квадратное уравнение, несколько способов графического решения уравнения
Индивидуальное решение контрольных заданий
Демонстрируют умение обобщения и систематизации знаний по основным темам раздела «Квадратичная функция».
Умение ясно, точно, грамотно излагать свои мысли в письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры.
Овладение навыками самоконтроля и оценки результатов своей деятельности, умениями предвидеть возможные результаты своих действий.
Осознанно и произвольно строят речевые высказывания в письменной форме.
Осознают качество и уровень усвоения
Умеют представлять конкретное содержание и сообщать его в письменной и устной форме.
Глава IV. Квадратные уравнения (20 ч)
59
1
Основные понятия.
Квадратное уравнение, старший коэффициент, второй коэффициент, свободный член, приведенное квадратное уравнение, полное квадратное уравнение, неполное квадратное уравнение, корень квадратного уравнения, решение квадратного уравнения.
Проблемные задания. Фронтальный опрос, упражнения
Имеют представление о полном и неполном квадратном уравнении, о решении неполного квадратного уравнения.
Самостоятельность в приобретении новых знаний и практических умений.
Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем.
Выделяют объекты и процессы с точки зрения целого и частей.
Составляют план и последовательность действий.
Устанавливают рабочие отношения, учатся эффективно сотрудничать и способствовать продуктивной кооперации.
60
2
Основные понятия.
Квадратное уравнение, старший коэффициент, второй коэффициент, свободный член, приведенное квадратное уравнение, полное квадратное уравнение, неполное квадратное уравнение, корень квадратного уравнения, решение квадратного уравнения.
Практикум. Индивидуальный опрос
Могут записать квадратное уравнение, если известны его коэффициенты
Умение ясно, точно, грамотно излагать свои мысли в устной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры.
Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни.
Выражают смысл ситуации различными средствами (рисунки, символы, схемы, знаки).
Сличают свой способ действия с эталоном.
Вступают в диалог, участвуют в коллективном обсуждении проблем, учатся владеть монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка.
61
3
Формулы корней квадратных уравнений.
Дискриминант квадратного уравнения, формулы корней квадратного уравнения, правило решения квадратного уравнения.
Проблемные задания. Фронтальный опрос, упражнения
Иметь представление о дискриминанте квадратного уравнения, формулах корней квадратного уравнения, об алгоритме решения квадратного уравнения.
Имеют представление о дискриминанте квадратного уравнения, формулах корней квадратного уравнения, об алгоритме решения квадратного уравнения.
Самостоятельность в приобретении новых знаний и практических умений.
Формирование умений выделять основное содержание прочитанного текста, находить в нем ответы на поставленные вопросы и излагать его
Умеют выбирать обобщенные стратегии решения задачи.
Определяют последовательность промежуточных целей с учетом конечного результата.
62
4
Формулы корней квадратных уравнений.
Дискриминант квадратного уравнения, формулы корней квадратного уравнения, правило решения квадратного уравнения.
Практикум. Индивидуальный опрос
Знать алгоритм вычисления корней квадратного уравнения, используя дискриминант.
Уметь решать квадратные уравнения по алгоритму.
Имеют представление о дискриминанте квадратного уравнения, формулах корней квадратного уравнения, об алгоритме решения квадратного уравнения.
Самостоятельность в приобретении новых знаний и практических умений.
Формирование умений выделять основное содержание прочитанного текста, находить в нем ответы на поставленные вопросы и излагать его
Умеют выбирать обобщенные стратегии решения задачи.
Определяют последовательность промежуточных целей с учетом конечного результата.
63
5
Формулы корней квадратных уравнений.
Дискриминант квадратного уравнения, формулы корней квадратного уравнения, правило решения квадратного уравнения.
Проблемные задания. Фронтальный опрос, упражнения
Знают алгоритм вычисления корней квадратного уравнения, используя дискриминант. Умеют решать простейшие квадратные уравнения с параметрами и проводить исследование всех корней квадратного уравнения с параметром
Формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта
Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.
Выделяют и формулируют познавательную цель.
Самостоятельно формулируют познавательную цель и строят действия в соответствии с ней.
Учатся разрешать конфликты - выявлять, идентифицировать проблемы, искать и оценивать альтернативные способы разрешения конфликта, принимать решение и реализовывать его.
64
6
Рациональные уравнения.
Рациональные уравнения, алгоритм решения рационального уравнения, проверка корней квадратного уравнения, посторонние корни.
Взаимопроверка в парах. Тренировочные упражнения
Имеют представление о рациональных уравнениях и о их решении. Знают алгоритм решения рациональных уравнений. Умеют решать рациональные уравнения, используя метод введения новой переменной
Креативность мышления, инициатива, находчивость, активность при решении математических задач
Овладение навыками организации учебной деятельности, постановки целей, планирования.
Осознанно и произвольно строят речевые высказывания в устной и письменной форме.
Сличают способ и результат своих действий с заданным эталоном, обнаруживают отклонения и отличия от эталона.
Учатся аргументировать свою точку зрения, спорить и отстаивать свою позицию невраждебным для оппонентов образом.
65
7
Рациональные уравнения.
Рациональные уравнения, алгоритм решения рационального уравнения, проверка корней квадратного уравнения, посторонние корни.
Проблемные задания. Фронтальный опрос, решение упражнений
Умеют решать рациональные уравнения по заданному алгоритму и методом введения новой переменной
Мотивация образовательной деятельности школьников на основе личностно ориентированного подхода
Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем.
Выбирают наиболее эффективные способы решения задачи в зависимости от конкретных условий.
Составляют план и последовательность действий.
Определяют цели и функции участников, способы взаимодействия.
66
8
Рациональные уравнения.
Рациональные уравнения, алгоритм решения рационального уравнения, проверка корней квадратного уравнения, посторонние корни.
Взаимопроверка в парах. Тренировочные упражнения
Умеют решать рациональные уравнения по заданному алгоритму и методом введения новой переменной
Мотивация образовательной деятельности школьников на основе личностно ориентированного подхода
Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем.
Выбирают наиболее эффективные способы решения задачи в зависимости от конкретных условий.
Составляют план и последовательность действий.
Определяют цели и функции участников, способы взаимодействия.
67
9
Рациональные уравнения как математические модели реальных ситуаций (текстовые задачи).
Рациональные уравнения, математическая модель реальной ситуации, решение задач на составление уравнений.
Фронтальный опрос. Решение качественных задач
Умеют решать рациональные уравнения, находить все решения уравнения, принадлежащие отрезку. Уметь решать задачи на числа, выделяя основные этапы математического моделирования.
Формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта
Умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки.
Определяют основную и второстепенную информацию.
Предвосхищают результат и уровень усвоения (какой будет результат?).
Планируют общие способы работы.
68
10
Рациональные уравнения как математические модели реальных ситуаций (текстовые задачи).
Рациональные уравнения, математическая модель реальной ситуации, решение задач на составление уравнений.
Работа с конспектом, с книгой и наглядными пособиями по группам
Могут свободно решать задачи на числа, выделяя основные этапы математического моделирования
Формирование ценностных отношений друг к другу, учителю, авторам открытий и изобретений, результатам обучения.
Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.
Ориентируются и воспринимают тексты художественного, научного, публицистического и официально-делового стилей.
Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению, осознают качество и уровень усвоения.
Обмениваются знаниями между членами группы для принятия эффективных совместных решений.
69
11
Рациональные уравнения как математические модели реальных ситуаций (текстовые задачи).
Рациональные уравнения, математическая модель реальной ситуации, решение задач на составление уравнений.
Работа с конспектом, с книгой и наглядными пособиями по группам
Могут свободно решать задачи на числа, выделяя основные этапы математического моделирования
Формирование ценностных отношений друг к другу, учителю, авторам открытий и изобретений, результатам обучения.
Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.
Ориентируются и воспринимают тексты художественного, научного, публицистического и официально-делового стилей.
Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению, осознают качество и уровень усвоения.
Обмениваются знаниями между членами группы для принятия эффективных совместных решений.
70
12
Контрольная работа № 4
Неполное квадратное уравнение, решение неполного квадратного уравнения. Дискриминант квадратного уравнения, формулы корней квадратного уравнения, правило решения квадратного уравнения. Системы уравнений, уравнений второй степени, задачи на составление системы уравнений.
Индивидуальное решение контрольных заданий
Демонстрируют умение обобщения и систематизации знаний по основным темам раздела «Квадратные уравнения».
Умение контролировать процесс и результат учебной математической деятельности.
Овладение навыками самоконтроля и оценки результатов своей деятельности, умениями предвидеть возможные результаты своих действий.
Осознанно и произвольно строят речевые высказывания в письменной форме.
Осознают качество и уровень усвоения.
Используют адекватные языковые средства для отображения своих чувств, мыслей и побуждений.
71
13
Частные случаи формулы корней квадратного уравнения.
Квадратное уравнение с четным вторым коэффициентом, формулы корней квадратного уравнения с четным вторым коэффициентом
Фронтальный опрос. Решение качественных задач
Знать алгоритм вычисления корней квадратного уравнения с четным вторым коэффициентом, используя дискриминант.
Свободное решение задач на движение по воде, выделяя основные этапы математического моделирования.
Способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Формирование умений воспринимать, перерабатывать и предъявлять информацию в словесной, образной, символической формах
Выбирают, сопоставляют и обосновывают способы решения задачи.
Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению, осознают качество и уровень усвоения.
Демонстрируют способность к эмпатии, стремление устанавливать доверительные отношения взаимопонимания.
72
14
Частные случаи формулы корней квадратного уравнения.
Квадратное уравнение с четным вторым коэффициентом, формулы корней квадратного уравнения с четным вторым коэффициентом
Проблемные задания. Фронтальный опрос, решение упражнения
Знать алгоритм вычисления корней квадратного уравнения с четным вторым коэффициентом, используя дискриминант.
Свободное решение задач на движение по воде, выделяя основные этапы математического моделирования.
Способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Формирование умений воспринимать, перерабатывать и предъявлять информацию в словесной, образной, символической формах
Выбирают, сопоставляют и обосновывают способы решения задачи.
Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению, осознают качество и уровень усвоения.
Демонстрируют способность к эмпатии, стремление устанавливать доверительные отношения взаимопонимания.
73
15
Теорема Виета. Разложение квадратного трехчлена на линейные множители.
Теорема Виета, обратная теорема Виета, симметрическое выражение с двумя переменными.
Фронтальный опрос. Решение качественных задач
Имеют представление о теореме Виета и об обратной теореме Виета, о симметрических выражениях с двумя переменными. Могут составлять квадратные уравнения по его корням, раскладывать на множители квадратный трехчлен
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту
Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
Осуществляют поиск и выделение необходимой информации.
Сличают свой способ действия с эталоном.
Учатся устанавливать и сравнивать разные точки зрения, прежде чем принимать решение и делать выбор.
74
16
Теорема Виета. Разложение квадратного трехчлена на линейные множители.
Теорема Виета, обратная теорема Виета, симметрическое выражение с двумя переменными.
Построение алгоритма действия, решение упражнений
Могут применять теорему Виета и обратную теорему Виета, решая квадратные уравнении. Умеют, не решая квадратного уравнения, вычислять выражения, содержащие корни этого уравнения в виде неизвестных, применяя обратную теорему Виета.
Формирование качеств мышления, необходимых для адаптации в современном информационном обществе
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Структурируют знания.
Предвосхищают временные характеристики достижения результата (когда будет результат?).
Интересуются чужим мнением и высказывают свое.
75
17
Иррациональные уравнения.
Иррациональные уравнения, метод возведения в квадрат, проверка корней, равносильные уравнения, равносильные преобразования уравнений, неравносильные преобразования уравнений.
Разноуровневые задания
Уметь решать иррациональные уравнения методом возведения в квадрат обеих частей уравнения, применяя свойства равносильных преобразований.
Формирование ответственного отношения к учению готовности и способности к саморазвитию
Формирование ответственного отношения к учению готовности и способности к саморазвитию
Осуществляют поиск и выделение необходимой информации.
Сличают свой способ действия с эталоном.
Учатся устанавливать и сравнивать разные точки зрения, прежде чем принимать решение и делать выбор.
76
18
Иррациональные уравнения.
Иррациональные уравнения, метод возведения в квадрат, проверка корней, равносильные уравнения, равносильные преобразования уравнений, неравносильные преобразования уравнений.
Построение алгоритма действия, решение упражнений
Уметь решать иррациональные уравнения методом возведения в квадрат обеих частей уравнения, применяя свойства равносильных преобразований.
Формирование качеств мышления, необходимых для адаптации в современном информационном обществе
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Структурируют знания.
Предвосхищают временные характеристики достижения результата (когда будет результат?).
Интересуются чужим мнением и высказывают свое.
77
19
Подготовка к контрольной работе.
Неполное квадратное уравнение, решение неполного квадратного уравнения. Дискриминант квадратного уравнения, формулы корней квадратного уравнения, правило решения квадратного уравнения. Системы уравнений, уравнений второй степени, задачи на составление системы уравнений.
Взаимопроверка в парах. Тренировочные упражнения
Демонстрируют умение обобщения и систематизации знаний по основным темам раздела «Квадратные уравнения».
Умение контролировать процесс и результат учебной математической деятельности.
Овладение навыками самоконтроля и оценки результатов своей деятельности, умениями предвидеть возможные результаты своих действий.
Осознанно и произвольно строят речевые высказывания в письменной форме.
Осознают качество и уровень усвоения.
Используют адекватные языковые средства для отображения своих чувств, мыслей и побуждений.
78
20
Контрольная работа № 5
Неполное квадратное уравнение, решение неполного квадратного уравнения. Дискриминант квадратного уравнения, формулы корней квадратного уравнения, правило решения квадратного уравнения. Системы уравнений, уравнений второй степени, задачи на составление системы уравнений.
Индивидуальное решение контрольных заданий
Демонстрируют умение обобщения и систематизации знаний по основным темам раздела «Квадратные уравнения».
Умение контролировать процесс и результат учебной математической деятельности.
Овладение навыками самоконтроля и оценки результатов своей деятельности, умениями предвидеть возможные результаты своих действий.
Осознанно и произвольно строят речевые высказывания в письменной форме.
Осознают качество и уровень усвоения.
Используют адекватные языковые средства для отображения своих чувств, мыслей и побуждений.
Глава V. Неравенства (17 ч)
79
1
Свойства числовых неравенств.
Числовые неравенства, сравнение чисел, знаки сравнения
Работа с опорными конспектами, работа с раздаточным материалом
Могут сравнивать числа одного знака на координатной прямой; записать числа в порядке возрастания и убывания
Представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации.
Выделять основное содержание прочитанного текста, находить в нем ответы на поставленные вопросы и излагать его
Выделяют количественные характеристики объектов, заданные словами
Сличают свой способ действия с эталоном.
Понимают возможность различных точек зрения, не совпадающих с собственной.
80
2
Свойства числовых неравенств.
Числовое неравенство, свойства числовых неравенств, неравенства одинакового смысла, неравенства противоположного смысла, среднее арифметическое, среднее геометрическое, неравенство Коши.
Самостоятельное выполнение упражнений и тестовых заданий
Могут выполнять действия с числовыми неравенствами; доказывать справедливость числовых неравенств при любых значениях переменных Знать свойства числовых неравенств. Иметь представление о неравенстве одинакового смысла, противоположного смысла.
Креативность мышления, инициатива, находчивость, активность при решении математических задач.
Овладение навыками самостоятельного приобретения новых знаний, организации учебной деятельности
Выделяют обобщенный смысл и формальную структуру задачи.
Вносят коррективы и дополнения в составленные планы.
Используют адекватные языковые средства для отображения своих чувств, мыслей и побуждений.
81
3
Свойства числовых неравенств.
Числовое неравенство, свойства числовых неравенств, неравенства одинакового смысла, неравенства противоположного смысла, среднее арифметическое, среднее геометрическое, неравенство Коши.
Построение алгоритма действия, решение упражнений, ответы на вопросы
Могут применять свойства числовых неравенств и неравенство Коши при доказательстве числовых неравенств.
Формирование качеств мышления, необходимых для адаптации в современном информационном обществе.
Умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки.
Умеют заменять термины определениями.
Самостоятельно формулируют познавательную цель и строят действия в соответствии с ней.
С достаточной полнотой и точностью выражают свои мысли в соответствии с задачами и условиями коммуникации.
82
4
Исследование функций на монотонность.
Возрастающая функция на промежутке, убывающая функция на промежутке, функция у=х2, функция у=1/х, функция у=√x, линейная функция. Монотонная функция.
Составление опорного конспекта, ответы на вопросы
Уметь построить и исследовать на монотонность функции: линейную, квадратную, обратной пропорциональности, функцию корень.
.
Способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Формирование умений анализировать и перерабатывать полученную информацию в соответствии с поставленными задачами.
Умеют выбирать смысловые единицы текста и устанавливать отношения между ними.
Вносят коррективы и дополнения в составленные планы.
Используют адекватные языковые средства для отображения своих чувств, мыслей и побуждений.
83
5
Исследование функций на монотонность.
Возрастающая функция на промежутке, убывающая функция на промежутке, функция у=х2, функция у=1/х, функция у=√x, линейная функция. Монотонная функция.
Составление опорного конспекта, ответы на вопросы
Уметь построить и исследовать на монотонность функции: линейную, квадратную, обратной пропорциональности, функцию корень.
.
Способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Формирование умений анализировать и перерабатывать полученную информацию в соответствии с поставленными задачами.
Умеют выбирать смысловые единицы текста и устанавливать отношения между ними.
Вносят коррективы и дополнения в составленные планы.
Используют адекватные языковые средства для отображения своих чувств, мыслей и побуждений.
84
6
Исследование функций на монотонность.
Возрастающая и убывающая на множестве, монотонная функция, исследование на монотонность
Практикум. Фронтальный опрос, работа с раздаточными материалами
Могут находить область определения и область значения по аналитической формуле. Умеют приводить примеры функций с заданными свойствами; строить кусочно-заданные функции.
Креативность мышления, инициатива, находчивость, активность при решении математических задач.
Овладение навыками самостоятельного приобретения новых знаний.
Выдвигают и обосновывают гипотезы, предлагают способы их проверки.
Сличают способ и результат своих действий с заданным эталоном, обнаруживают отклонения и отличия от эталона.
Развивают умение интегрироваться в группу сверстников и строить продуктивное взаимодействие со сверстниками и взрослыми.
85
7
Решение линейных неравенств.
Линейное неравенство с одним неизвестным, левая и правая части неравенства, член неравенства, решение неравенства
Выполнение заданий из учебника и печатной тетради, обсуждение решений
Знают, как выглядят линейные неравенства. Могут записать в виде неравенства математические утверждения.
Умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры.
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Выбирают вид графической модели, адекватной выделенным смысловым единицам.
Составляют план и последовательность действий.
Понимают возможность различных точек зрения, не совпадающих с собственной.
86
8
Решение линейных неравенств.
Линейное неравенство с одним неизвестным, левая и правая части неравенства, член неравенства, решение неравенства
Индивидуальная работа. Работа в парах.
Знают, как по графику линейной функции записать неравенство, какие значения принимают переменные величины.
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту
Анализировать и перерабатывать полученную информацию в соответствии с поставленными задачами, выделять основное содержание прочитанного текста, находить в нем ответы на поставленные вопросы и излагать его.
Выбирают знаково-символические средства для построения модели.
Определяют последовательность промежуточных целей с учетом конечного результата.
Определяют цели и функции участников, способы взаимодействия.
87
9
Решение квадратных неравенств.
Квадратное неравенство с одной переменной, частное и общее решения, равносильность, равносильные преобразования.
Построение алгоритма действия, решение упражнений, ответы на вопросы
Могут решать квадратные неравенства, применяя разложение на множители квадратного трехчлена.
Знать, как решать квадратное неравенство по алгоритму и методом интервалов.
Готовность к выбору жизненного пути в соответствии с собственными интересами и возможностями.
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Выделяют объекты и процессы с точки зрения целого и частей.
Ставят учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что еще неизвестно.
Обмениваются знаниями между членами группы для принятия эффективных совместных решений
88
10
Решение квадратных неравенств.
Квадратичная функция, график квадратичной функции, интервал, числовые промежутки, эскиз графика функции, направление веток.
Построение алгоритма действия, решение упражнений, ответы на вопросы
Могут построить эскиз квадратичной функции, провести исследование по нему и решить квадратное неравенство.
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту
Умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации.
Выбирают вид графической модели, адекватной выделенным смысловым единицам.
Принимают познавательную цель, сохраняют ее при выполнении учебных действий, регулируют весь процесс их выполнения и четко выполняют требования познавательной задачи.
Учатся переводить конфликтную ситуацию в логический план и разрешать ее как задачу через анализ условий.
89
11
Зачет № 6.
Метод интервалов, числовые промежутки, исследование знака, область постоянного знака.
Фронтальный опрос. Выборочный диктант. Решение качественных задач
Уметь обобщать и систематизировать знания и умения по данной теме.
Объясняют отличия в оценках одной и той же ситуации разными людьми, дают адекватную оценку результатам своей учебной деятельности, проявляют интерес к предмету
Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
Составляют план и последовательность действий
Выбирают знаково-символические средства для построения модели
Общаются и взаимодействуют с партнерами по совместной деятельности или обмену информацией
90
12
Приближенные значения действительных чисел., погрешность приближения, приближение по недостатку и избытку.
Приближенное значение по недостатку, приближенное значение по избытку, округление чисел, погрешность приближения, абсолютная погрешность, правило округления, относительная погрешность.
Взаимопроверка в парах. Работа с опорным материалом
Знают о приближенном значении по недостатку, по избытку, округлении чисел, погрешности приближения, абсолютной и относительной погрешностях.
Самостоятельность в приобретении новых знаний и практических умений.
Формирование умений анализировать и перерабатывать полученную информацию в соответствии с поставленными задачами.
Применяют методы информационного поиска, в том числе с помощью компьютерных средств
Предвосхищают результат и уровень усвоения (какой будет результат?).
Описывают содержание совершаемых действий с целью ориентировки предметно-практической или иной деятельности.
91
13
Приближенные значения действительных чисел., погрешность приближения, приближение по недостатку и избытку.
Оценка абсолютной погрешности, приближенное значение по недостатку, приближенное значение по избытку, точность измерения
Решение упражнений. Составление опорного конспекта, ответы на вопросы
Могут дать оценку абсолютной погрешности, если известны приближения с избытком и недостатком.
Формирование ценностных отношений друг к другу, учителю, авторам открытий и изобретений, результатам обучения.
Формирование умений воспринимать, перерабатывать и предъявлять информацию в словесной, образной, символической формах.
Структурируют знания.
Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению, осознают качество и уровень усвоения.
Адекватно используют речевые средства для дискуссии и аргументации своей позиции.
92
14
Приближенные значения действительных чисел., погрешность приближения, приближение по недостатку и избытку.
Округление чисел, приближенное значение числа, правило округления, округление с точностью.
Взаимопроверка в парах. Работа с опорным материалом
Могут любое дробное число представить в виде десятичной дроби с разной точностью и найти абсолютную погрешность каждого приближения
Формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта
Формирование умений выделять основное содержание прочитанного текста, находить в нем ответы на поставленные вопросы и излагать его.
Осознанно и произвольно строят речевые высказывания в устной и письменной форме.
Ставят учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что еще неизвестно.
Умеют слушать и слышать друг друга.
93
15
Стандартный вид положительного числа.
Стандартный вид положительного числа, порядок числа, запись числа в стандартной форме, действия над числами.
Взаимопроверка в группе. Практикум
Знают о стандартном виде положительного числа, о порядке числа, о записи числа в стандартной форме. Могут выполнять простейшие действия над числами, записанными в стандартном виде.
Умение контролировать процесс и результат учебной математической деятельности.
Овладение навыками самоконтроля и оценки результатов своей деятельности, умениями предвидеть возможные результаты своих действий.
Выделяют и формулируют проблему.
Вносят коррективы и дополнения в составленные планы.
Определяют цели и функции участников, способы взаимодействия.
94
16
Подготовка к контрольной работе.
Метод интервалов, числовые промежутки, исследование знака, область постоянного знака. Стандартный вид положительного числа, порядок числа, запись числа в стандартной форме, действия над числами. Округление чисел, приближенное значение числа, правило округления, округление с точностью.
Взаимопроверка в парах. Тренировочные упражнения
Демонстрируют умение обобщения и систематизации знаний по основным темам раздела «Неравенства».
Умение контролировать процесс и результат учебной математической деятельности.
Овладение навыками самоконтроля и оценки результатов своей деятельности, умениями предвидеть возможные результаты своих действий.
Осознанно и произвольно строят речевые высказывания в письменной форме.
Осознают качество и уровень усвоения.
Используют адекватные языковые средства для отображения своих чувств, мыслей и побуждений.
95
17
Контрольная работа № 6.
Метод интервалов, числовые промежутки, исследование знака, область постоянного знака. Стандартный вид положительного числа, порядок числа, запись числа в стандартной форме, действия над числами. Округление чисел, приближенное значение числа, правило округления, округление с точностью.
Индивидуальное решение контрольных заданий
Демонстрируют умение обобщения и систематизации знаний по основным темам раздела «Неравенства».
Умение контролировать процесс и результат учебной математической деятельности.
Овладение навыками самоконтроля и оценки результатов своей деятельности
Осознанно и произвольно строят речевые высказывания в письменной форме.
Осознают качество и уровень усвоения.
Проявляют уважительное отношение к партнерам, внимание к личности другого, адекватное межличностное восприятие.
Итоговое повторение (10ч).
96
1
Итоговое повторение (комбинированный)
Основная теорема арифметики, доказательство числовых неравенств.
Решение качественных задач. Работа с раздаточным материалом
Могут применять свойства числовых неравенств и неравенство Коши при доказательстве числовых неравенств.
Воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения
Первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов.
Проводят анализ способов решения задачи с точки зрения их рациональности и экономичности.
Вносят коррективы и дополнения в составленные планы.
Используют адекватные языковые средства для отображения своих чувств, мыслей и побуждений.
97
2
Итоговое повторение (комбинированный)
Решение линейных и квадратных неравенств, исследование функции на монотонность.
Решение качественных задач. Работа с раздаточным материалом
Могут решать линейные и квадратные неравенства с одной переменной; проводить исследование функции на монотонность.
Формирование качеств мышления, необходимых для адаптации в современном информационном обществе.
Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни.
Умеют выбирать обобщенные стратегии решения задачи.
Вносят коррективы и дополнения в способ своих действий в случае расхождения эталона, реального действия и его продукта.
Умеют слушать и слышать друг друга.
98
3
Итоговое повторение (комбинированный)
Квадратный корень из произведения, квадратный корень из дроби, вычисление корней.
Работа с конспектом, с книгой и наглядными пособиями по группам
Знают свойства квадратных корней. Могут применять данные свойства корней при нахождении значения выражений.
Развитие интереса к математическому творчеству и математических способностей.
Разработка теоретических моделей процессов или явлений.
Структурируют знания.
Составляют план и последовательность действий.
Проявляют готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции.
99
4
Итоговое повторение (комбинированный)
Формулы корней квадратного уравнения, теорема Виета, разложение квадратного трехчлена на множители.
Решение качественных задач. Работа с раздаточным материалом
Могут решать квадратные уравнения по формулам корней квадратного уравнения через дискриминант.
Убежденность в возможности познания природы, в необходимости разумного использования достижений науки и технологий для дальнейшего развития человеческого общества, уважение к творцам науки и техники, отношение к математике как элементу общечеловеческой культуры.
Формирование умений анализировать и перерабатывать полученную информацию в соответствии с поставленными задачами.
Выбирают наиболее эффективные способы решения задачи в зависимости от конкретных условий.
Ставят учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что еще неизвестно
Умеют (или развивают способность) брать на себя инициативу в организации совместного действия.
100
5
Итоговое повторение (учебный практикум)
Функция у = ах2 +вх + с, квадратичная функция, график квадратичной функции, ось параболы, формула абсциссы параболы, направление веток параболы, алгоритм построения параболы у = ах2 +вх + с.
Взаимопроверка в группе. Решение логических задач
Могут применять теорему Виета и обратную теорему Виета, не решая квадратные уравнения.
Креативность мышления, инициатива, находчивость, активность при решении математических задач.
Овладение навыками организации учебной деятельности, постановки целей, планирования.
Самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера.
Сличают способ и результат своих действий с заданным эталоном, обнаруживают отклонения и отличия от эталона.
Умеют (или развивают способность) с помощью вопросов добывать недостающую информацию.
Итоговое повторение (учебный практикум)
101
6
Итоговое повторение (учебный практикум)
Функция у = ах2 +вх + с, квадратичная функция, график квадратичной функции, ось параболы, формула абсциссы параболы, направление веток параболы, алгоритм построения параболы у = ах2 +вх + с.
Взаимопроверка в группе. Решение логических задач
Могут применять теорему Виета и обратную теорему Виета, не решая квадратные уравнения.
Креативность мышления, инициатива, находчивость, активность при решении математических задач.
Овладение навыками организации учебной деятельности, постановки целей, планирования.
Самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера.
Сличают способ и результат своих действий с заданным эталоном, обнаруживают отклонения и отличия от эталона.
Умеют (или развивают способность) с помощью вопросов добывать недостающую информацию.
102
7
Итоговая контрольная работа (обобщение и систематизация знаний)
По всему курсу алгебры 8 класса
Индивидуальное решение контрольных заданий
Демонстрируют умение обобщения и систематизации знаний по основным темам курса алгебры 8 класса.
Умение контролировать процесс и результат учебной математической деятельности.
Овладение навыками самоконтроля и оценки результатов своей деятельности, умениями предвидеть возможные результаты своих действий.
Осознанно и произвольно строят речевые высказывания в письменной форме.
Осознают качество и уровень усвоения, оценивают достигнутый результат.
Понимают возможность различных точек зрения, не совпадающих с собственной.
103
8
Итоговое повторение (учебный практикум)
Весь курс алгебры 8 класса
Демонстрируют умение обобщения и систематизации знаний по основным темам курса алгебры 8 класса.
Креативность мышления, инициатива, находчивость, активность при решении математических задач.
Овладение навыками самоконтроля и оценки результатов своей деятельности, умениями предвидеть возможные результаты своих действий.
Самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера.
Предвосхищают результат и уровень усвоения (какой будет результат?).
Учатся организовывать и планировать учебное сотрудничество с учителем и сверстниками.
Весь курс алгебры 8 класса
104
9
Итоговое повторение (учебный практикум)
Весь курс алгебры 8 класса
Демонстрируют умение обобщения и систематизации знаний по основным темам курса алгебры 8 класса.
Креативность мышления, инициатива, находчивость, активность при решении математических задач.
Овладение навыками самоконтроля и оценки результатов своей деятельности, умениями предвидеть возможные результаты своих действий.
Самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера.
Предвосхищают результат и уровень усвоения (какой будет результат?).
Учатся организовывать и планировать учебное сотрудничество с учителем и сверстниками.
Весь курс алгебры 8 класса
105
10
Итоговое повторение (учебный практикум)
Весь курс алгебры 8 класса
Демонстрируют умение обобщения и систематизации знаний по основным темам курса алгебры 8 класса.
Креативность мышления, инициатива, находчивость, активность при решении математических задач.
Овладение навыками самоконтроля и оценки результатов своей деятельности, умениями предвидеть возможные результаты своих действий.
Самостоятельно создают алгоритмы деятельности при решении проблем творческого и поискового характера.
Предвосхищают результат и уровень усвоения (какой будет результат?).
Учатся организовывать и планировать учебное сотрудничество с учителем и сверстниками.
Весь курс алгебры 8 класса