Конспект по математике на тему Уравнение касательной

Урок: Уравнение касательной к графику функции

Цель урока: На уроке рассмотреть тему «Уравнение касательной к графику функции». Вывести уравнение касательной к графику функции. Затем, чтобы успешно решать задачи на касательную, рассмотреть смысл каждого его элемента.

1. Уравнение касательной к графику функции

На предыдущих занятиях были рассмотрены задачи на технику дифференцирования. Это очень важные задачи, и нахожде­ние производных необходимо в разных задачах, в том числе и в составлении уравнения касательной.

Построим кривую (см. рис.1).

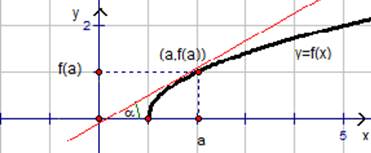
Рис. 1. График функции .

Зафиксируем точку х=а. Если х=а, то значение функции равно . Значит, имеем точку с координатами (.

Задача: составить уравнение касательной. Более строгая формулировка - написать уравнение касательной к функции в точке с абсциссой х=а, в которой - существует.

Уравнение касательной - это прямая, которая задается формулой

Любая прямая, в том числе и касательная, определяется двумя числами: и . Исходя из геометрического смысла производ­ной (тангенс угла наклона касательной) - это есть угловой коэффициент .

Параметр найдем из условия, что касательная проходит через точку (, то есть .

.

Стало быть .

Запишем уравнение касательной

.

Или, .

Получили уравнение касательной к кривой в точке с абсциссой .

2. Смысл элементов уравнения касательной

Смысл каждого элемента, который входит в уравнение касательной.

1) ( - точка касания касательной и графика функции.

2) - угловой коэффициент касательной к графику функции.

3) - произвольная точка на касательной.

Очень много задач, когда задана точка, которая не лежит на графике функции, и через нее надо провести касательную к данной функции. Надо четко понимать, что - это произвольная точка на касательной.

Итак, получили уравнение касательной, проанализировали смысл каждого элемента этой касательной, и теперь приведем пример, и на нем изложим методику построения касательной.

3. Алгоритм составления уравнения касательной к графику функции

Задача.

К кривой в точке с абсциссой провести касательную. Проиллюстрируем поиск касательной на рисунке (см. рис.2).

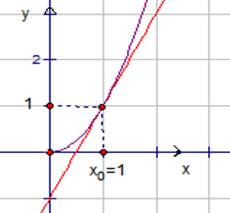
Рис. 2. Касательная к графику функции .

Зафиксируем точку . Значение функции в этой точке равно 1.

Алгоритм составления уравнения касательной к графику функции:

1) Найти и точку касания.

- дано.Точка касания: (;.

2) Найти производную в любой точке .

.

3) Найти значение производной в точке с абсциссой .

4) Выписать и проанализировать уравнение касательной.

.

Упрощаем и получаем: .

Ответ: .

4. Сопутствующие задачи

Задача 1.

Пусть дано уравнение касательной .

Найдите точки пересечения касательной с осями координат.

Если , то . - это первая точка.

Если , то . - вторая точка.

Итак, первая точка - это точка с координатами . Вторая точка - точка пересечения с осью , точка с координатами (см. рис.3).

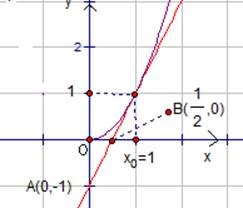
Рис.3. Точки пересечения касательной к графику функции с осями координат. Задача 2.

Найти длину отрезка касательной, которая отсекается осями координат, то есть надо найти длину отрезка .

Рассмотрим прямоугольный треугольник (Рис. 3). Длина катета равна 1. Длина катета . Длину отрезка из прямоугольного треугольника найдем по теореме Пифагора:

Задача 3.

Найти площадь треугольника, образованного касательной и осями координат. Ясно, что это площадь треугольника (Рис. 3) - площадь треугольника, образованного касательной и осями координат.

Следующая задача для самостоятельного решения.

Найдите радиус окружности, вписанной в треугольник . Радиус окружности, описанной около треугольника .

5. Касательная к графику тригонометрической функции

Рассмотрим пример.

Дана функция . Написать уравнение касательной к данной кривой в точке с данной абсциссой.

Рассмотрим графическую иллюстрацию (см. рис.4).

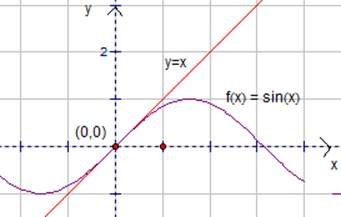
Рис. 4. Касательная к графику функции .

Нахождение точки касания.

1. Точка касания имеет координаты .

2. Найти .

3. Найти

И, последнее действие, - написать уравнение касательной.

4. .

Упростим и получим .

Заметим в точке (0;0) синусоида и касательная соприкасаются. В районе точки х=0 синусоида и прямая почти не различаются.

6. Итог урока

Итак, мы вывели уравнение касательной. Рассмотрели все элементы этой касательной. Выяснили их смысл. Сформулировали одну из методик нахождения касательных в конкретных функциях, в конкретных точках и решили некоторые сопутствующие задачи.

Список рекомендованной литературы

1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.

2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уро­вень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.

4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвеще­ние, 1997.

5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.

6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.

7. ЗвавичЛ.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изуче­нием математики (дидактические материалы).-М.: Дрофа, 2002.

8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов обще­образов. учреждений).-М.: Просвещение, 2003.

9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просве­щение, 2006.

</ 10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983