Применение математических моделей в реальных условиях практической деятельности обучаемых»

«Применение математических моделей в реальных условиях практической деятельности обучаемых» Автор:. Пластун С.В. Костанайский современный многопрофильный

колледж г.Костанай

Актуальность исследования темы обусловлена тем, что при прохождении производственной практики студенты затруднялись при решении экономической задачи применить алгебру матриц.

Проблема исследования: недостаточно выработаны навыки

использования математических моделей в решении экономических задач.

Задача исследования:

• показать методику применения математической модели при вычислении данных, решая экономическую задачу конкретного предприятия.

В основу исследования положена гипотеза: если четко соблюдать методику применения математической модели при решении задач экономического содержания, то будут выработаны практические навыки в ее применении.

Объект исследования: ОБУЧАЕМЫЕ группы ОУ-12 - КСМК.

Математический анализ дает ряд фундаментальных понятий, которыми оперирует экономист, - это функция, предел, производная, интеграл, дифференциальное уравнение и алгебра матриц. В данной работе речь пойдет об алгебре матриц, так как решение задач экономического характера производится при помощи матриц.

Впервые понятие алгебра матриц было сформулировано в виде математической модели в 1936г. в трудах известного американского экономиста В.В. Леонтьева, который попытался проанализировать причины экономической депрессии США 1929-1932г.г.

Рассмотрим пример, рассчитанный в условиях практической работы, с использованием таблицы. Таблица содержит данные баланса трёх отраслей предприятия ТОО «Иволга Холдинг» за определенный период времени, которые собрали учащиеся третьего курса, проходившие практику в 2009 году. Требуется найти объем валового выпуска каждого вида продукции, если конечное потребление по отраслям увеличить соответственно до 60,70 и 30 тыс. тенге.

Решение.

х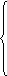_ij =a_ijx_j; i,j = 1,2,…….,n (1)

x₁ = a₁₁x₁ + a₁₂x₂ + … + a_1nx_n + y₁

x₂ = a₂₁x₁ + a₂₂x₂ + … + a_2nx_n + y₂ (2)

_{………………………………………………………}

x₃ = a_n1x₁ + a_n2x₂ + … + a_nnx_n + y_n

Выпишем векторы валового выпуска, конечного потребления и матрицу коэффициентов прямых затрат. Согласно формам (1) и (2), имеем

100 40

x = 100 y = 60 (3)

50 10

0,05 0.35 0.40

А = 0,10 0.10 0.40

0.20 0.10 0.20

Матрица А удовлетворяет обоим критериям продуктивности. В случае заданного увеличения конечного потребления новый вектор конечного продукта будет иметь следующий вид

100

x = 100 (3.1)

50

Требуется найти новый вектор валового выпуска х, удовлетворяющий соотношениям баланса в предложении, что матрица А не изменяется. В таком случае компоненты х₁, х₂, х₃ неизвестного вектора х находятся из системы уравнений, которая согласно форме (2) имеет в данном случае вид

x₁ = 0,05х₁ + 0,35x₂ + 0,4x₃ + 60

x₂ = 0,1x₁ + 0,1x₂ + 0,4x₃ + 70 (4)

x₃ = 0,2x₁ + 0,1x₂ + 0,2x₃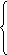

+ 30

В матричной форме эта система выглядит следующим образом:

X = AX + Y (5)

или (E-A) X = Y (5.1)

X = (E-A)^-1Y = SY (6)

где матрица (Е - А)^-1 имеет вид

0,95 -0,35 -0,40 60

(Е-А)^-1 = -0,10 0,90 -0,40 Y = 70 (7)

-0,20 -0,10 0,80 30

Решение системы линейных уравнений (4) при заданном векторе правой части (3.1) (например, методом Гаусса) дает новый вектор х как решение системы уравнений баланса (5):

152,6

х = 135,8 (тыс.тенге) (8)

92,5

Данный пример решения экономической задачи, основанный на конкретном фактическом материале, свидетельствует о том, что обучаемые, освоив методику использования математической модели, доказали гипотезу:

у учащихся сформированы практические навыки в применении математической модели при решении задач экономического содержания.

Использование элементов алгебры матриц является одним из основных методов решения многих экономических задач. Особенно этот вопрос стал актуальным при разработке и использовании баз данных: при работе с ними почти вся информация хранится и обрабатывается в матричной форме.

Математическая модель является не только мощным средством для решения прикладных задач и универсальным языком науки, но и элементом общей культуры. В связи с этим математическое образование следует рассматривать как важнейшую составляющую в системе фундаментальной подготовки современного экономиста.

Список использованной литературы.

1. Колесников А.Н. Краткий курс математики для экономистов, учебное пособие ИНФРА - М, 2001г.

2. Красс М.С. Математика для экономических специальностей, М., 2002г.

3. Кремер Н.Ш. Высшая математика для экономических специальностей, Москва Высшее образование, 2007г.

4. Черняк В. Сборник задач по экономике, Москва 2006г.