26 вариантов ЕГЭ по математике образца 2016г

</ Вариант 1.

1. В школе 1050 учеников, из них 30% - ученики начальной школы. Среди учеников средней и старшей школы 20% изучало французский язык. Сколько учеников в школе изучают французский язык, если в начальной школе французский язык не изучается?

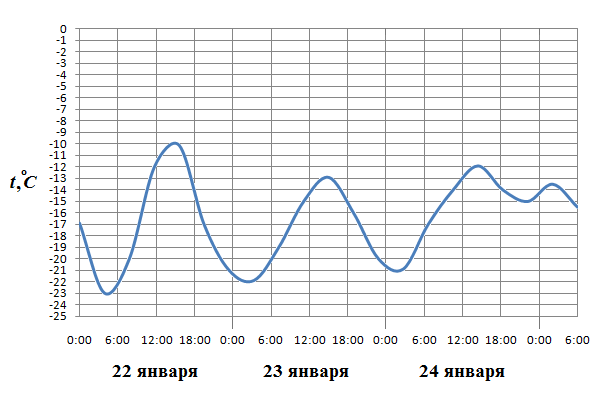
2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали - значение температуры в градусах Цельсия. Определите по рисунку наименьшую температуру воздуха 23 января. Ответ дайте в градусах Цельсия.

3. 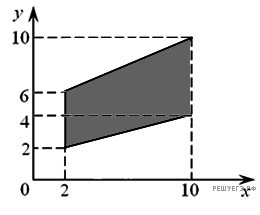Найдите площадь трапеции, вершины которой имеют координаты (2; 2), (10; 4), (10; 10), (2; 6).

4. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Сапфир» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Сапфир» выиграет жребий ровно два раза.

5. Найдите корень уравнения .

6. 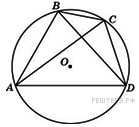Четырехугольник ABCD вписан в окружность. Угол ABD равен 75°, угол CAD равен 35°. Найдите угол ABC. Ответ дайте в градусах.

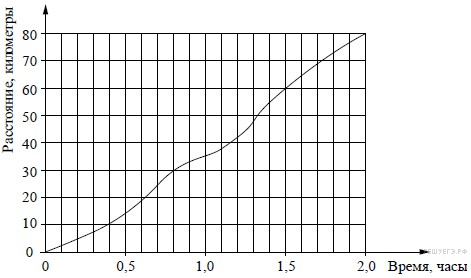
7. На рисунке показан график движения автомобиля по маршруту. На оси абсцисс откладывается время (в часах), на оси ординат - пройденный путь (в километрах). Найдите среднюю скорость движения автомобиля на данном маршруте. Ответ дайте в км/ч.

8. Высота конуса равна 72, а длина образующей - 90. Найдите диаметр основания конуса.

9. Найдите значение выражения при .

10. При нормальном падении света с длиной волны нм на дифракционную решётку с периодом нм наблюдают серию дифракционных максимумов. При этом угол (отсчитываемый от перпендикуляра к решетке), под которым наблюдается максимум, и номер максимума связаны соотношением Под каким минимальным углом (в градусах) можно наблюдать второй максимум на решётке с периодом, не превосходящим 1800 нм.

11. Смешали некоторое количество 11-процентного раствора некоторого вещества с таким же количеством 13-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

12. Найдите наибольшее значение функции на отрезке

13. а) Решите уравнение .

б) Найдите все корни этого уравнения, принадлежащие отрезку .

14. В основании прямой треугольной призмы ABCA₁B₁C₁ лежит равнобедренный прямоугольный треугольник ABC с гипотенузой AB, равной ; высота призмы равна Найдите расстояние от точки C₁ до плоскости BCM, где M - середина ребра A₁C₁.

15. Решите неравенство:

16. Две окружности, радиусы которых равны 9 и 4, касаются внешним образом. Найдите радиус третьей окружности, которая касается двух данных окружностей и их общей внешней касательной.

17. По вкладу «А» банк в конце каждого года планирует увеличивать на 20% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» - увеличивать эту сумму на 10% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.

18. При каких уравнение имеет ровно три корня?

19. Семь экспертов оценивают кинофильм. Каждый из них выставляет оценку - целое число баллов от 0 до 12 включительно. Известно, что все эксперты выставили различные оценки. По старой системе оценивания рейтинг кинофильма - это среднее арифметическое всех оценок экспертов. По новой системе оценивания рейтинг кинофильма оценивают следующим образом: отбрасываются наименьшая и наибольшая оценки и подсчитывается среднее арифметическое оставшихся оценок.

а) Может ли разность рейтингов, вычисленных по старой и новой системам оценивания, равняться

б) Может ли разность рейтингов, вычисленных по старой и новой системам оценивания, равняться

в) Найдите наибольшее возможное значение разности рейтингов, вычисленных по старой и новой системам оценивания.