Тема: Цилиндр и конус

Тема: "Цилиндр и конус"

11-й класс

Цели урока:

образовательные: систематизировать, обобщить и закрепить изученный материал по данной теме и научить применять их при решении задач;

развивающие: развивать пространственное восприятие, навыки самоконтроля, логическое мышление, математически грамотную речь, прививать бережное отношение к природе;

воспитательные: совершенствовать навыки самостоятельной работы, воспитывать внимание, аккуратность.

Тип урока: урок-практикум (решение задач по теме: «Цилиндр и конус»).

Оборудование: ТСО, модели тел вращения, карточки с заданиями, настенные таблицы с задачами.

Этапы урока

І. Организационный момент

• постановка целей и задач урока,

• вступительное слово учителя.

Уроки-практикумы по решению задач занимают важное место в школьном курсе математики, так как основным итогом любой изучаемой темы является умение применять полученные знания на практике.

Сегодня на уроке мы не только обобщим теоретические знания по теме «Цилиндр и конус», но и повторим некоторые разделы планиметрии, так как решение стереометрических задач в конечном итоге зачастую сводится к решению серии планиметрических задач.



ІІ. Проверка домашнего задания (чертежи тел вращения)

ІІІ. Проверка формул •

Найди ошибку в записи формул:

боковой поверхности цилиндра (S = 2πRH);

• полной поверхности цилиндра (S=2ΠR(R + H));

• боковой поверхности усеченного конуса S = π(R +r)l;

• длины окружности (C = 2πR);

• радиуса описанной окружности для правильных многоугольников ﴾R = ﴿;

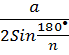• радиуса описанной окружности

для произвольного треугольника (R = );• площади треугольника S=abSinα; S=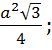 S= S=);• теорему синусов ﴾= =

• боковой поверхности конуса (S = πRl);

• полной поверхности конуса (S=ΠR(R + l));

• боковой поверхности усеченного конуса

(S = π(R +r)l;

S= S=);

• площади круга (S = π);

• площади кругового сектора ();

• радиуса вписанной окружности

для правильных многоугольников ﴾R = ﴿;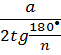

• радиуса вписанной окружности

для произвольного треугольника (R = );

• площади параллелограмма (S=;

S=abSinα;

• теорему косинусов ﴾=

ТЕСТ

1. Какая фигура является основанием цилиндра

а) окружность;

б) круг;

в) эллипс.

2. Назовите отрезок, который является радиусом:

а) О₂А₁;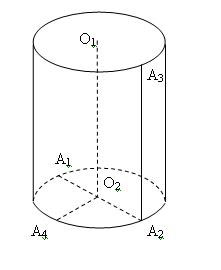

б) О₂О₁;

в) А₄О₂.

3. Укажите на рисунке образующую цилиндра:

а) О₁О₂;

б) А₂А₃;

в) А₁А₂.

4. Высота цилиндра это:

а) Расстояние между плоскостями его основания;

б) отрезок, который соединяет две любые точки оснований;

в) отрезок, который соединяет центр круга с любой точкой цилиндра.

5. Какая фигура является осью цилиндра?

а) прямая О₁О₂;

б) отрезок О₁О₂;

в) отрезок А₁А₂.

6. Равносторонний цилиндр - это цилиндр, у которого:

а) образующая равна высоте;

б) радиус основания равен высоте цилиндра;

в) диаметр основания равен высоте цилиндра.

7. Масса тела вычисляется по формуле:

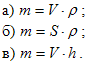
8. Буквой обозначают:

а) площадь;

б) плотность;

в) температуру.

9. Укажите номера правильных выражений:

а) 1 см = 10 мм;

б) 1м³ = 1000000 см³;

в) 1 см³ = 0,000001 м³.

10. Объем цилиндра вычисляется по формуле:

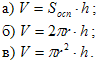
Ключ к тесту:

1. Б.

2. А, В.

3. Б.

4. А.

5. А.

6. В.

7. А.

8. Б.

9. А, Б, В.

10 А, В.

На экране вы видите ключ к тесту и критерий для самооценки своих знаний.

• «5» 9-10 правильных ответов.

• «4» 7-8правильных ответов.

• «3» 5-6правильных ответов.

И поставьте оценку, подпишите работы и сдайте.

ІV. Решение задач

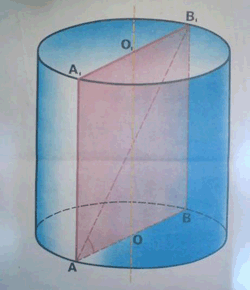
Задача 1.(устно) Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 60° и равна 20 см.

Найдите высоту, радиус основания цилиндра, длину окружности основания и площадь боковой поверхности цилиндра.

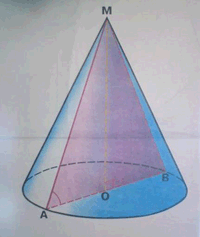
Задача 2.(устно) Образующая конуса равна 18 см и наклонена к плоскости основания под углом 60°.

Найдите радиус основания, высоту конуса, площадь осевого сечения и площадь полной поверхности конуса.

Задача 3. Треугольник АВС со сторонами АВ = 41 см, АС = 15 см и ВС = 52 см вращается вокруг прямой, содержащей его большую сторону.

Найдите высоты конусов, из которых составлено тело вращения, площадь осевого сечения и площадь полной поверхности тела вращения.

Задача 4. Радиус основания цилиндра равен 12 см. Его сечение плоскостью, параллельной оси цилиндра и удаленной от нее на 6 см, является квадратом.

Найдите высоту цилиндра, площади сечения и полной поверхности цилиндра.

Задача 5. Радиусы оснований усеченного конуса 12 см и 6 см, высота его равна 8 см.

Найдите образующую усеченного конуса, площадь осевого сечения, площадь боковой и полной поверхности усеченного конуса.

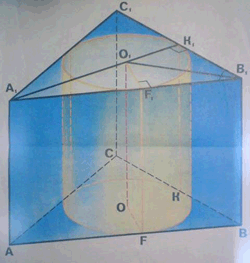
Задача 6. Прямая призма, основанием которой является равнобедренный треугольник с основанием a и прилежащим к нему углом α, описана около цилиндра.

Высота призмы равна H.

Найдите радиус основания цилиндра, площадь осевого сечения цилиндра, площадь боковой поверхности призмы и цилиндра.

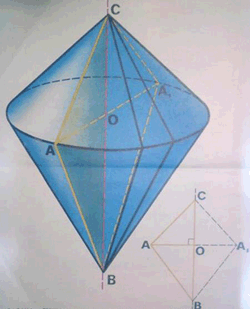
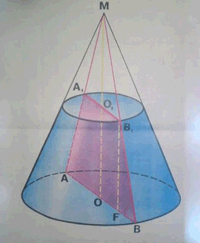
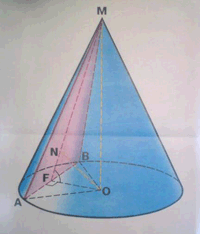
Задача 7. Через вершину конуса и хорду АВ основания конуса, равную 16 см, проведено сечение, образующее с плоскостью основания угол 60°. Радиус основания конуса равен 10 см.Найдите высоту конуса, расстояние от центра основания до плоскости сечения и площадь полной поверхности конуса.

Задача 8. Прямоугольный параллелепипед со сторонами 6 дм и 8 дм и высотой, равной 14 дм, вписан в цилиндр.

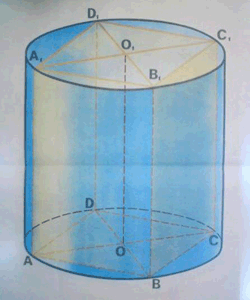
Найдите радиус основания цилиндра, площадь осевого сечения цилиндра, площадь полной поверхности цилиндра и параллелепипеда.

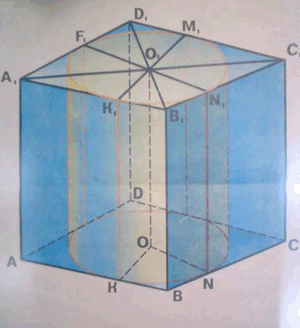
Задача 9. Около цилиндра, высота которого 15 см, а радиус основания 5 см, описана прямая призма. Основанием ее является ромб со стороной 12 см.

Найдите радиус основания, площадь осевого сечения цилиндра, площадь боковой поверхности призмы и цилиндра.

Задача 10. Около конуса, высота которого равна см и радиус основания 10 см, описана пирамида. Основанием пирамиды является ромб с острым углом 30°.

Найдите угол наклона образующей конуса к плоскости основания, площадь осевого сечения конуса, площадь полной поверхности конуса.

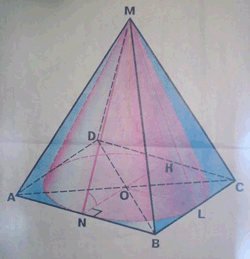
Задача11. В конус, высота которого 20 см, вписана пирамида. Основанием пирамиды является прямоугольник со сторонами 18 см и 20 см.

Найдите образующую и радиус основания конуса, площади поверхностей конуса и пирамиды.

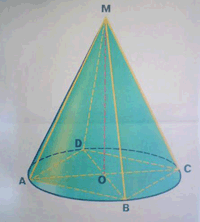
Задача 12. В конус вписана правильная пирамида. Ее высота равна Н, боковое ребро наклонено к плоскости основания под углом α.

Найдите образующую и радиус основания конуса, площадь полной поверхности конуса.

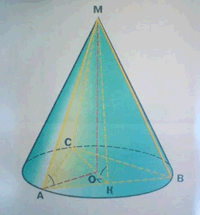
Задача 13. Тело получено при вращении ромба со стороной 18 см и углом 60° вокруг стороны.

Найдите расстояние от его образующей до оси вращения, высоты получившихся конуса и цилиндра, площадь полной поверхности тела вращения.

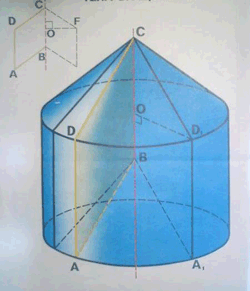
Дополнительные задачи

Задача 14. Диагональ осевого сечения цилиндра равна 8√2 см и образует с плоскостью основания угол 45°. Найдите площадь полной поверхности цилиндра.

Задача 15. Высота конуса равна 2 √3 см. Найдите площадь осевого сечения конуса, если оно является правильным треугольником.

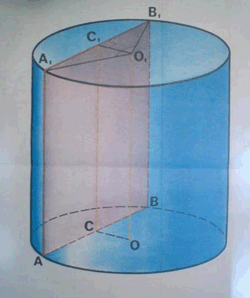
Задача 16. Радиусы оснований усеченного конуса равны 3 см и 6 см, а высота равна 4 см. Найдите площадь осевого сечения и боковой поверхности усеченного конуса.

V. Контроль и оценка знаний

Контроль за правильностью выполнения заданий осуществляется учителем вовремя решения задач учащимися, как у доски, так и на местах

VІ. Итог урока

Подведение итогов, выставление оценок.

VІІ. Домашнее задание: Изготовить модель:

цилиндра и конуса, №8-16.