- Учителю
- Урок по геометрии в 10 классе
Урок по геометрии в 10 классе
Разработка урока по геометрии в 10 классе
Тема. Решение задач по теме «Пирамида».
Тип урока: урок повторения и обобщения.
Форма организации урока: традиционная с использованием информационных технологий.
Образовательная цель:
-
повторение и закрепление знаний по изучаемой теме (формулировки и понятия, связанные с пирамидой и её элементами);
-
отработка умений учащихся пользоваться сведениями из тригонометрии;
-
совершенствование вычислительных навыков;
-
развитие умения решать задачи с применением теорем (признак параллельности прямой и плоскости), понятия «угол между прямой и плоскостью);
Развивающая цель.
-
Развитие аналитического мышления посредством выбора более рациональных подходов к решению задачи;
-
Развитие пространственных представлений и образного мышления;
-
Формирование общеучебных компетенций (применение ранее изученных сведений при решении задач, в новых ситуациях);
-
Развитие быстроты реакции, внимания, приёмов кодирования информации.
Воспитательная цель.
-
Формирование позитивного отношения к использованию электронных учебных материалов;
-
Развитие познавательной активности;
Оснащение урока: мультимедиапроектор, экран, доска, электронные учебные материалы с диска: «Открытая математика 10.Стереометрия» (разделы «Пирамида. Параллельность прямых и плоскостей»),презентация со слайдами пошагового решения задачи.
Урок проводится в компьютерном классе.
Учебник: «Геометрия, 10-11, Л.С.Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др., М.:Просвещение, 2005г
Ход урока.
I. Актуализация опорных знаний.
1. Двое учащихся на доске записывают решение домашних задач.
1
a). Дано: ДАВС - правильная треугольная пирамида, АВ =АС =ВС =а , ДО=Н, ДО- высота
Найти: АД, угол АДВ.
Решение:
-
АК=а 3\2, О-центр описанной окружности.
-
АО=2\3 АК =а\3(или из формулы а3 = R 3,
-
Из треугольника АОД, АД = АО2 + ОД2 =…..
б). Из треугольника DLR sin DLR= …ученик № 254(а, б).
2 ученик № 254(в,г)
Найти: угол ДАК; угол АКД.
Решение:
в). угол ОАД - искомый, tg ОАД= ДО\АО, tg ОАД = Н а 3=…
г). угол ОКД - искомый……….
2. Ученик работает по карточке индивидуального опроса.
Задача: Дано: ДАВС- правильная треугольная пирамида, О- центр треугольника АВС (точка пересечения медиан), МС-медиана треугольника АВС, ВС=3 3, ДС=5.
Найти: S МДС
Решение:
-
ДО- высота пирамиды, МС=ВС sin 600.
МС=….
ОС- МС= ….
-
Из треугольника ДОС: ДО=…..
-
S ДМС = МС ДО= 9
Ответ: 9.
3. С остальными учащимися в это время проводится фронтальный опрос по рисунку, спроецированному на экран.
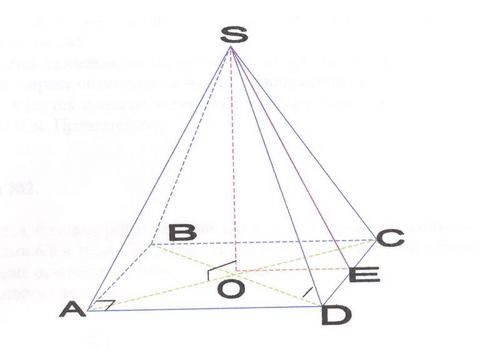
Вопросы:
-
Что называется пирамидой?
-
Что представляет собой сечения пирамиды плоскостями, проходящими через ее вершину?
-
Какое сечение пирамиды называется диагональным сечением?
-
Какая пирамида называется правильной? Что такое ось правильной пирамиды?
-
Будет ли пирамида правильной, если её боковыми гранями являются правильные треугольники?
-
Сколько граней, перпендикулярных к плоскости основания может иметь пирамиды?
-
Существует ли четырехугольная пирамида, у которой противоположные боковые грани перпендикулярны к основании?
-
Могут ли все грани треугольной пирамиды быть прямоугольными треугольниками?
-
Каким образом можно вычислите площадь боковой поверхности пирамиды?
-
Как правильно построить чертеж правильной четырехугольной пирамиды? (используя возможности диска, учитель меняет изображение пирамиды, поясняет как выполнить оптимальный рисунок для успешного решения задачи).
-
Где находится центр основания правильной четырехугольной пирамиды на проекционном чертеже?
-
Куда проецируется точка, равноудаленная от всех сторон многоугольника?
4. Проверяется домашнее и индивидуальные задания у доски.
III. Формирование умений и навыков учащихся.
Сейчас мы займемся построением сечения пирамиды.
Задача№1.
Условие задачи на экране.
Построить сечение пирамиды DАВС плоскостью, проходящей через точку М, лежащую на стороне основания АВ, точку С и параллельно ребру АD.
Перед решением задачи повторяется признак параллельности прямой и плоскости. При решении задачи учащимся предлагается изобразить пирамиду и отметить точку М.
Обращается внимание на то, правильно ли сделан рисунок и показывается на экране оптимальный вариант изображения пирамиды.
Рассматривается пошаговое решение задачи с использованием компьютера.
1. В плоскости АВD через точку М проведем прямую MN //AD, N принадлежит DВ.
Вопрос: почему MN проводим параллельно AD?
2. В плоскости АВС проведем прямую МС.
Вопрос: Что можно сказать о принадлежности прямой МС плоскости основания пирамиды и плоскости сечения?
3. В плоскости ВDС проводим прямую NC.
4. Плоскость МNC -искомая. Плоскость МNC параллельна ребру АD
Вопрос. Почему МNC // АD?
Задача №2.
Пирамида, боковые ребра которой 13 см, в основании треугольник со сторонами 6, 8 и 10см. Доказать, что одна из боковых граней перпендикулярна основанию. Найдите высоту пирамиды и площадь полной поверхности пирамиды.
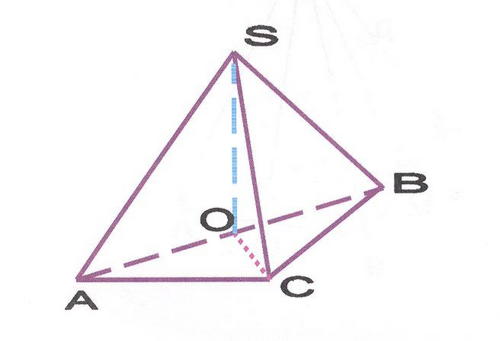
На первом этапе обращается внимание на правильное выполнение рисунка. После выполнения рисунка каждый учащийся самостоятельно решает задачу.
На втором этапе решения задачи развирается каждый шаг решения задачи. Весь класс работает совместно с учителем. Для этого с помощью проектора на экран выводится слайд с заданиями и рисунком. Идет совместное обсуждение этапов решения задачи., а затем учитель предлагает посмотреть правильное решение этой задачи.
На этом этапе происходит окончательная оценка своих успехов по решению задачи каждым учащимся.
Разбирая решение каждого шага, ученик сам находит в своем решении ошибки или открывает для себя более рациональное и последовательное решение.
Задача №3. Закрепляется навык построения чертежа.
В основании треугольной пирамиды лежит равнобедренный треугольник АВС, угол С прямой. Длины боковых ребер пирамиды равны b, длина гипотенузы основания с. Найдите углы, которые боковые ребра образуют с основанием.
Проверяется решение задачи.
Итоги урока.
-
На экзамене по математике включены задачи по геометрии, поэтому мы должны развивать навыки решения задач.
-
Но пренебрегать теорией нельзя, так как без знания теоретического материала невозможно успешно решать задачи.
Задание на дом.
-
Закончить задачу №3 с дополнительным условием: найти двугранный угол при ребре СS.
-
выполнить задание №306, п.28,29,30.