Урок-лекция. Простейшие тригонометрические уравнения. Урок №1

Урок №1

Тема . Простейшие тригонометрические уравнения .

Цель . Усвоение учащимися вывода и использование формул для определения корней уравнения sin x = a , cos x = a , tg x = a , ctg x = a .

Тип урока. Урок - лекция

Мотивация обучения .

Решая квадратные уравнения , мы пользовались выведенными формулами корней , что значительно упрощало работу . Выведем формулы корней тригонометрических уравнений для упрощения их решения .

Объявляется тема и дидактическая цель урока .

Изучение нового материала .

I. Определение . Равенство тригонометрических выражений , содержащих неизвестное только под знаком тригонометрических функций называется тригонометрическим уравнением .

sin x = a

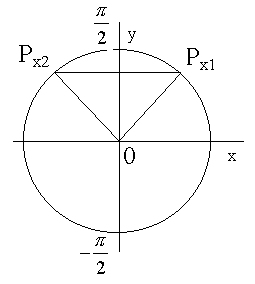Если а > 1 , то уравнение sin x = a не имеет решений , так как sin x  1 для любого х . Отложим на оси ординат а - значение синуса. Этому значению на единичной окружности соответствуют точки и , причём .

На этом отрезке функция синус возрастает и уравнение sin x = a имеет единственный корень

х₁ = arcsin a.

На отрезке функция синус убывает и принимает все значения от - 1 до 1 . По теореме о корне уравнение имеет один корень x₂ =  - arcsin a /

Итак , с учётом периодичности уравнение sin x = a имеет два решения

х₁ = arcsin a + 2n, n  Z

x₂ =  - arcsin a + 2n , n  Z .

Удобно записывать эти оба решения одной формулой :

х =(-1)^k arcsin a + k, k  Z .

Если k = 2n , то х₁ = arcsin a + 2pn, n Î Z .

Если k = 2n + 1 ,то x₂ =  - arcsin a + 2n , n  Z .

При изучении свойств функции у = sin x мы находили путём логических рассуждений нули функции из условия sin x = 0 , экстремальные точки из условия sin x = 1 и sin x = - 1 . Фактически мы находили корни особых случаев решения уравнения sin x = а .

Они имели вид :

sin x = 0 х = n, n  Z .

sin x = 1 х = + 2pn, n Î Z .

sin x = -1 х = -+ 2pn, n Î Z .

Примеры

1. sin x =

х =(-1)^k arcsin + k, k  Z .

так как arcsin = , то

х =(-1)^k + k, k  Z .

2. sin 2x = -

2х =(-1)^k arcsin + k, k  Z .

так как arcsin = - arcsin = - , то

2х =(-1)^k+1 + k, k  Z .

х =(-1)^k+1 + , k  Z .

II. cos x = a

Если а > 1 , то уравнение cos x = a не имеет решений , так как  cos x   1 для любого х . Пусть  а   1 . Надо найти все такие числа х , для которых cos x = a . На отрезке существует одно такое решение - это арккосинус числа а.

Косинус чётная функция , и , значит , на отрезке уравнение имеет в точности одно решение , это число - arccos a.

Итак, уравнение cos x = a на отрезке длиной 2 имеет два решения :

х₁ = arccos a ,

х₂= - arccos a.

Вследствие периодичности функции косинус все остальные решения отличаются от этих на 2n , n Z и объединяются в одну формулу :

х =  arccos a + 2n , n Z .

Решение уравнения можно проиллюстрировать на единичной окружности .

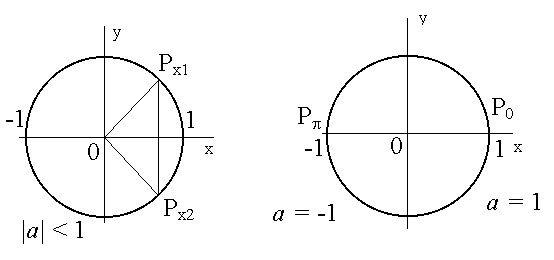
По определению cos x - это абсцисса точки Р_х единичной окружности . Если а < 1 , то таких точек две ; если же а = 1 или а = - 1 , то одна .

При а = 1 числа arccos a и - arccos a совпадают ( они равны нулю ) , поэтому решением уравнения cos x=1 будет х = 2 n , n Z .

При а = - 1 имеем : cos x= -1 х =  + 2 n , n Z .

При а = 0 имеем : cos x= 0 х = +  n , n Z .

Примеры :

1. cos x=

х =  arccos + 2p n , nÎ Z .

так как arccos = , то

х =  + 2p n , nÎ Z .

Ответ :  + 2p n , nÎ Z .

3. tg x = a

При любом а на интервале имеется только одно значение х , такое число х , что tg x = a - это arctg a.

Поэтому уравнение tg x = a на интервале имеет единственный корень . Функция у = tg x периодическая , её наименьший период . Следовательно , остальные корни отличаются от найденного на n ,

х = arctg a + n , nÎ Z .

Решение уравнения tg x = a проиллюстрируем на единичной окружности .

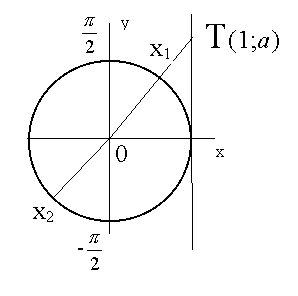
Для любого числа а на линии тангенсов есть лишь одна точка с ординатой а , это точка

Т ( 1 ; а ). Прямая ОТ пересекается с единичной окружностью ; при этом интервалу

соответствует точка х₁ правой полуокружности , такая , что х = arctg a .

Для уравнения сtg x = a корень х = arсctg a + n , nÎ Z .

Примеры :

1. tg x =

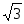
х = arctg + pn , nÎ Z .

х = + pn , nÎ Z .

Ответ : х = + pn , nÎ Z .

2. сtg x =

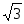
Это уравнение можно решить двумя способами .

I . tg x = II . сtg x =

х = arctg + pn , nÎ Z ; х = arcctg + pn , nÎ Z;

х = + pn , nÎ Z ; х = + pn , nÎ Z ;

Ответ : х = + pn , nÎ Z .

Домашнее задание : уч. Никольский С.М. п 11.1 . № 11.2 ( а-в) , 11.3(а-в) .

Итог урока : 1. С какими новыми уравнениями познакомились ?

2. Каковы формулы корней простейших

тригонометрических уравнений ?