Муниципальное бюджетное общеобразовательное учреждение Аксайского района Грушевская средняя общеобразовательная школа

_______________________________________________________________

ПРОЕКТ

Задачи на смеси и сплавы

Шеховцова Анастасия Дмитриевна,

ученица 9 класса МБОУ Грушевской СОШ

Руководитель: Дружинина Любовь Михайловна,

учитель математики МБОУ Грушевской СОШ

Ст. Грушевская

2016

Оглавление

Оглавление 1

Введение 3

Глава 1. Теоретические аспекты темы 5-6

Глава 2. Примеры решения задач 7-14

Заключение 15

Список используемых источников 16

Введение

Введение новых образовательных стандартов требует не только знаний у учащихся, но и умение их применять. Это нашло отражение в новой демоверсии КИМ - 2013 по математике, в которой заметно увеличилось количество задач практической направленности. В связи с этим появилась необходимость в усилении практической направленности в решении задач, включая соответствующие задания на проценты, пропорции, графики реальных зависимостей, текстовые задачи с построением математических моделей реальных ситуаций, а также задачи на смеси и сплавы.

Проанализировав учебники математики 5-11 классов, можно сделать вывод, что задачи на смеси и сплавы в курсе школьной математики почти не рассматриваются. Так, например, в 6 классе таких задач 4, в 7 классе-1 задача, в 8 классе-3 задачи, в 9 классе-2 задачи, в 10, 11 классах -1задача. Возникает необходимость дополнительно изучить данную тему.

Тема проекта: «Задачи на смеси и сплавы».

Межпредметные связи: химия, биология.

Цель проекта: создание сборника задач на смеси и сплавы.

Для реализации этой цели необходимо решить следующие задачи:

1. Изучить литературу по данной теме, осуществить поиск нужной информации в Интернете.

2. Проанализировать и систематизировать собранную информацию.

3. Закрепить и расширить знания по избранной теме.

4. Подготовить отчет в бумажном и электронном виде.

Этот проект является практико-ориентированным. В результате работы над проектом должен быть создан конечный продукт - небольшой сборник задач на сплавы и смеси, который можно будет использовать на уроках математики, химии, биологии, а так же при подготовке выпускников ГИА и ЕГЭ.

Был разработан план работы над проектом:

• октябрь 2011 - подготовительный этап;

• ноябрь, декабрь 2012 - сбор и подготовка материалов;

• январь, февраль 2013 - реализация проекта, подготовка отчета.

Работа велась во внеурочное время под руководством учителя математики.

Ожидаемые результаты:

• расширение математических знаний по теме сплавы и смеси;

• развитие навыков поиска и систематизации информации;

• получение конечного продукта, который может найти практическое применение.

Глава 1.

Но первом этапе необходимо повторить такие понятия как:

1.концентрация (доля чистого вещества в смеси (сплаве));

2.масса смеси (сплава);

3.масса чистого вещества в смеси (сплаве).

А также, то, что процентом называется его сотая часть и три основные задачи на проценты:

1. Найти 15% от числа 60.

Решение:60•0,15=9.

2. Найти число, 12% которого равны 30.

Решение: 30:0,12=250.

3. Сколько процентов составляет число 120 от 600?

Решение: 120:600•100%=20%

Концентрация раствора - это отношение объема (массы) вещества к объему (массе) раствора, записанное в процентах. Чтобы найти ее нам нужно решить три следующие задачи:

а) найти объем вещества в каждом из растворов;

б) найти объем вещества в смеси;

в) найти объем смеси;

г) найти отношение объема вещества, содержащейся в смеси и объема самой смеси и выразит это отношение в процентах.

Для решения задач такого типа требуется выполнить три простых шага:

1. Составляем таблицу, в которой указываем общую массу и массу «чистого» вещества для каждой смеси или сплава. Все данные берутся прямо из условия задачи. Например, 50 литров кислоты с концентрацией 15% - это m₀ = 50 литров общей массы и m₁ = 0,15 · 50 = 7,5 литров «чистого» вещества.

2. Если какие-то ячейки таблицы остались не заполненными, обозначаем их переменными x, y и т.д. Чаще всего в качестве неизвестной величины выступает масса, реже - концентрация.

3. Составить уравнения по правилу: при объединении двух смесей/сплавов их массы складываются. Другими словами, масса полученной смеси равна сумме масс исходных смесей. Аналогично, складываются массы «чистых» веществ.

Прежде чем записать ответ, необходимо вернуться к задаче и еще раз прочитать, что требуется найти. Потому что решить уравнение - это еще не значит решить текстовую задачу.

Глава 2.

Рассмотрим несколько примеров решения таких задач.

Задача 1.Смешали 4 л 15%-ного раствора соли с 5 л 20%-ного соли к смеси добавли 1 л чистой воды. Какова концентрация полученной смеси?

Рещение.

Запишем условие задачи в виде таблицы, считая, что чистая вода это раствор, содержащий 0 литров соли.

1-й раствор

2-й раствор

3-й раствор

смесь

вода

100%

соль

15%

20%

0%

расствор

4 л

100%

5 л

100%

1 л

100%

1. Объем соли в 1-м растворе. 40, 0,15 = 0,6 (л);

2. Объем соли в 2-м растворе . 50,2 = 1 (л);

3. Объем соли в смеси. 0,6 + 1 + 0 = 1,6(л);

4. Объем смеси. 4 + 5 + 1 = 10(л);

5. Концентрация соли в смеси. (1,6 : 10)100 =16%.

Ответ: 16%.

Задача 2.Сколько килограммов олова нужно добавить к куску бронзы массой 4 кг и содержащему 15% олова, чтобы повысить содержание в нем олова до 25% от общей массы?

Рещение.

Запишем условие задачи в виде таблицы, считая, что смешали два сплава, причем второй сплавсодержит 100% олова и не содержит остальных компонентов.

1-й сплав

2-й сплав

новый сплав

олово

15%

100%

60%

остальные компоненты

0%

сплав

4 кг

В данной задаче известно процентное содержание компонента, поэтому мы можем количество этого компонента во втором сплаве считать равным х кг и выразить отношение массы олова в новом сплаве к массе сплава через х .

1. Масса олова в первом сплаве 40,15 =0,6 (кг);

2. Масса олова во втором сплаве х (кг);

3. Масса олова в новом сплаве 0,6 + х (кг);

4. Масса второго сплава х (кг);

5. Масса нового сплава 4 + х (кг);

6. Отношение массы олова в новом сплаве к массе нового сплава (0,6 + х):(4 + х), по условию задачи оно должно быть равно 0,6. Имеем уравнение

(0,6 + х):(4 + х) = 0,6. Это уравнение равносильно уравнению

5(0,6 + х) = 3(4 + х);

5х - 3х = 12 - 3;

х = 4,5.

Ответ: 4,5 кг.

Задача 3.Сплав меди и олова массой 10 кг содержит 70% олова. К этому сплаву добавили 8 кг меди. Сколько нужно добавить килограмм олова, чтобы его концентрация стала в 3 раза больше, чем концентрация меди?

Рещение.

Запишем условие задачи в виде таблицы, считая что к первому сплаву добавили второй сплав содержащий х кг олова и 8 кг меди.

1-й сплав

2-й сплав

новый сплав

олово

70%

х кг

3

медь

8 кг

1

сплав

10 кг

100%

100%

100%

По условию задачи концентрация меди в новом сплаве должна быть в три раза выше, чем концентрация олова. Этот факт мы используем для составления уравнения. Пусть концентрация меди равна t%, тогда концентрация олова 3t%, так как суммарная концентрация меди и олова должна быть равной 100% (других компонентов в сплаве нет), имеем уравнение t + 3t = 100, откуда концентрация меди равна 25%, а концентрация олова равна 75%.

1. Масса олова в первом сплаве 100,7 = 7 (кг);

2. Масса олова во втором сплаве х кг;

3. Масса олова в новом сплаве х + 7 (кг);

4. Масса ноавого сплава 10 + 8 + х (кг)

5. Концентрация олова в новом сплаве (х + 7):( 18 +х), имеем второе уравнение.

(х + 7):( 18 + х) = 0,75;

4(х + 7) = 3(18 + х);

4х - 3х = 54 - 28;

х = 26.

Ответ: 26 кг.

Задача 4. Первоначально влажность зерна составляла 25%. После того как 200 кг зерна просушили, оно потеряло в массе 30 кг. Вычислить влажность просушенного зерна.

Рещение.

В данной ситуации мы имеем дело не с раствором, а со смесью "твердого" зерна и воды. Запишем условие задачи в виде таблицы, учитывая тот факт, что сушка приводит к уменьшению массы воды в смеси и массу самой смеси.

1-я смесь

2-я смесь

вода

m

25%

m - 30

?

зерно

смесь

200 кг

100%

200-30

100%

1. Масса воды в 1-й смеси 200 0,25 = 50 (кг);

2. Масса 2-й смеси 50 - 30 = 20 (кг);

3. Масса второй смеси 200 - 30 = 170 (кг);

4. Процент влажности второй смеси (20:170)100 =11,8%.

Ответ: 11,8%..

Задача 5. Сухие грибы содержат 12% воды, а свежие - 90% воды. Сколько получится сухих грибов из 22 кг свежих грибов?

Решение.

свежие грибы

сухие грибы

вода

90%

12%

"мякоть"

смесь

22> кг

100%

?

100%

При сушке грибов, ягод, фруктов происходит испарение воды, поэтому масса воды уменьшается, а масса "мякоти" сохраняется неизменной.

1. Процентное содержание "мякоти" в свежих грибах 100% - 90% = 10%;

2. Масса "мякоти" 22 0,1 = 2,2 (кг);

3. Процентное содержание мякоти в сухих грибах 100% - 12% = 88%;

4. Пусть масса сушенных грибов х (кг);

5. Отношение массы "мякоти" к массе сушенных грибов 2,2 : х, что по условию задачи равно 0,88.

Имеем уравнение 2,2 : х = 0,88;

х = 2,2:0,88;

х = 2,5;

Ответ: 2,5 кг.

Задача 6. Сначала приготовили 25% раствор поваренной соли. Затем одну треть воды испарили. Найти концентрацию получившегося раствора.

Рещение.

Запишем условие задачи в виде таблицы.

раствор

новый раствор

соль

25%

?

вода

-1/3

раствор

100%

100%

Процентное содержание воды в растворе 100% - 25% = 75%.

Пусть масса раствора была х кг, тогда масса соли в растворе 025х кг, масса воды 0,75х кг.

Одну треть воды испарили, значит, уменьшилась как масса воды в растворе, так и масса самого раствора, количество соли в растворе не изменилось.

Масса воды в новом растворе 0,75х - 0,25х = 0,5х (кг).

Масса нового раствора х - 0,25х = 0,75х (кг).

Концентрация нового раствора (0,25х : 0,75х)100 = 33,7%.

Ответ: 33,7%.

Задача 7.Имеется 1 литр 6% раствора спирта. Сколько литров 3%-ного раствора спирта нужно добавить в первй раствор, чтобы получить 5% раствор.

Рещение.

Запишем условие задачи в виде таблицы.

1-й раствор

2-й раствор

новый раствор

спирт

6%

3%

5%

вода

раствор

1 л

100%

?

100%

Рещение.

Объем спирта в 1-м растворе 10,06=0,06 (л).

Пусть объем второго раствора равен х л.

Объем спирта во втором растворе 0,03х (л).

Объем спирта в новом растворе 0,06 + 0,03х (л).

Объем нового раствора 1 + х (л).

Концентрация нового раствора (0,06 + 0,03х) : (1 + х). По условию задачи она должна быть равной 0,05. Имеем уравнение

(0,06 + 0,03х) : (1 + х) = 0,05;

20(0,06 + 0,03х) = 1 + х;

х - 0,6х = 1,2 - 1;

х = 0,5;

Ответ: 0,5 л.

Итак, из приведенных выше задач можно сделать следующие выводы:

Масса раствора равна сумме масс воды и соли.

Масса сплава равна сумме масс металлов, входящих в этот сплав.

Масса смеси равна сумме масс компонентов этой смеси.

Концентрация соли или процентное содержание соли в растворе - это отношение массы соли к массе раствора, записанное в виде процентов.

Чтобы найти на сколько процентов большее число больше меньшего числа, можно:

1. Вычесть из большего числа меньшее число.

2. Полученное число разделить на меньшее число.

3. Полученное число умножить на сто.

Чтобы найти на сколько процентов меньшее число меньше большего числа, можно:

1. Вычесть из большего числа меньшее число.

2. Полученное число разделить на большее число.

3. Полученное число умножить на сто.

Один процент от числа - это сотая часть от этого числа.

Приведем еще несколько примеров решения таких задач, решив их несколькими способами.

Задача 1. Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?

Р

200гешение.

1-й способ.

Пусть хг - масса первого сплава. Тогда, (200-х)г - масса второго сплава.

Сумма масс меди в двух первых сплавах (то есть слева от знака равенства) равна массе меди в полученном третьем сплаве (справа от знака равенства):

Решив это уравнение, получаем х=140. При этом значении х выражение 200-х=60. Это означает, что первого сплава надо взять140г, а второго-60г.

Ответ:140г. 60г.

2-й способ.

Пусть х г и у г - масса соответственно первого и второго сплавов, то есть легко устанавливается каждое из уравнений системы двух линейных уравнений с двумя переменными:

Решение системы приводит к результату: Значит, первого сплава надо взять 140 г, а второго-60 г.

Ответ: 140г,60г.

Аналогичные рассуждения позволяют справиться и с более сложными задачами рассматриваемого вида.

Задача 2. Имеются три смеси, составленные из трех элементов A, B и С. В первую смесь входят только элементы А и В в весовом отношении 1:2, во вторую смесь входят только элементы В и С в весовом отношении 1:3, в третью смесь входят только элементы А и С в весовом отношении 2:1. В каком отношении нужно взять эти смеси, чтобы во вновь полученной смеси элементы А, В и С содержались в весовом отношении 11:3:8?

Решение.

Предшествующая работа позволяет без проблем составить одну из схем, где за х единиц веса, у единиц веса и z единиц веса обозначены соответственно вес первой, второй и третьей смеси.

П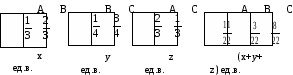одсчет и уравнивание веса любых двух из трех компонентов рассматриваемых смесей приводит к системе двух уравнений с тремя переменными. Если рассмотрим компоненты А и В, то система имеет вид:

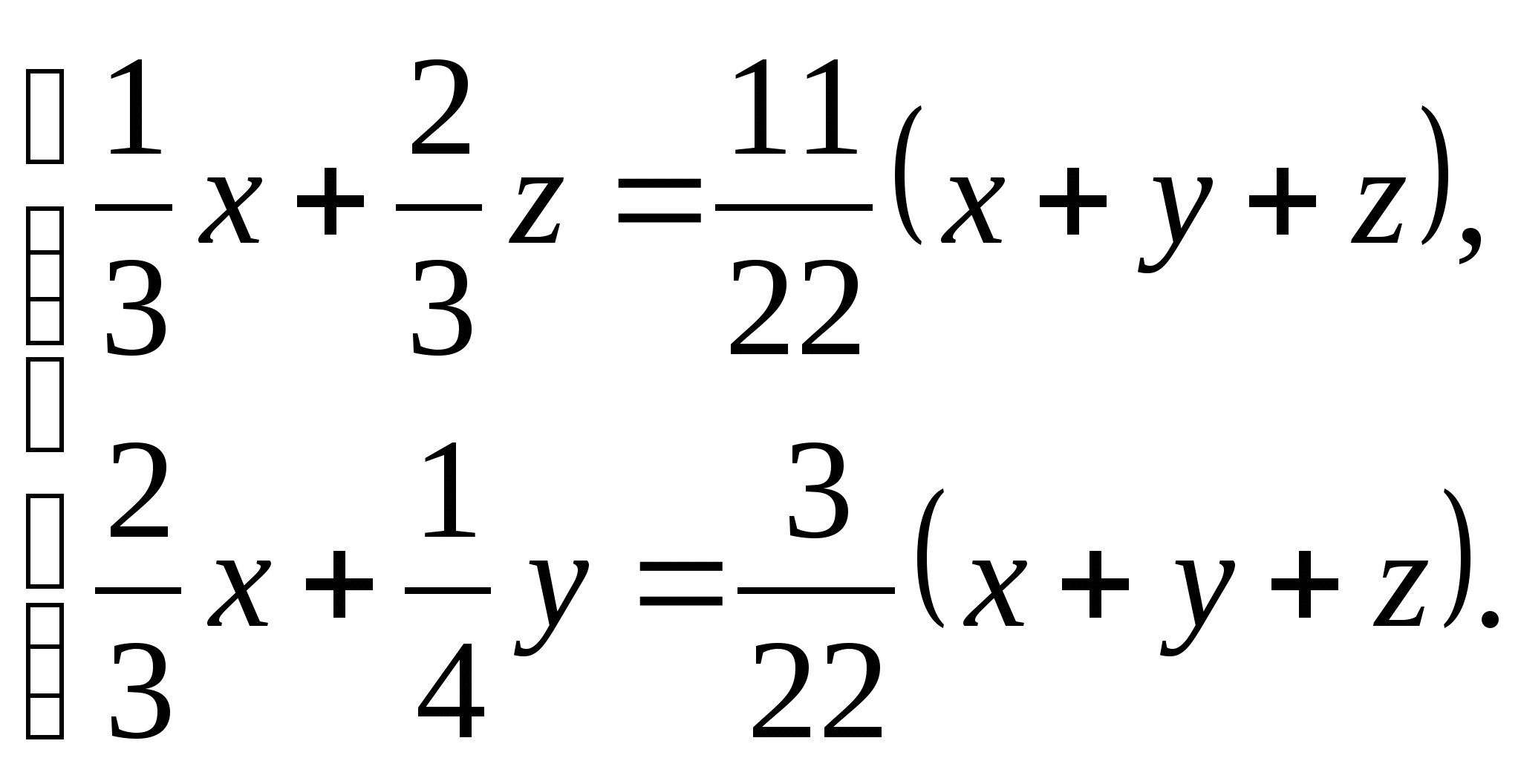
Решение этой системы может вызвать затруднения: количество уравнений (их два) меньше числа переменных (их три). Навести на решение поможет правило: составить выражение, значение которого надо найти по вопросу задачи. Это выражение имеет вид: x:y:z. Значит, для ответа на вопрос задачи совсем не обязательно находить значение каждой из переменных. Достаточно найти два отношения x:y и y:z или x:y и z:y. Для нахождения двух последних отношений разделим левую и правую части каждого уравнения на у (у≠0).Получаем систему:

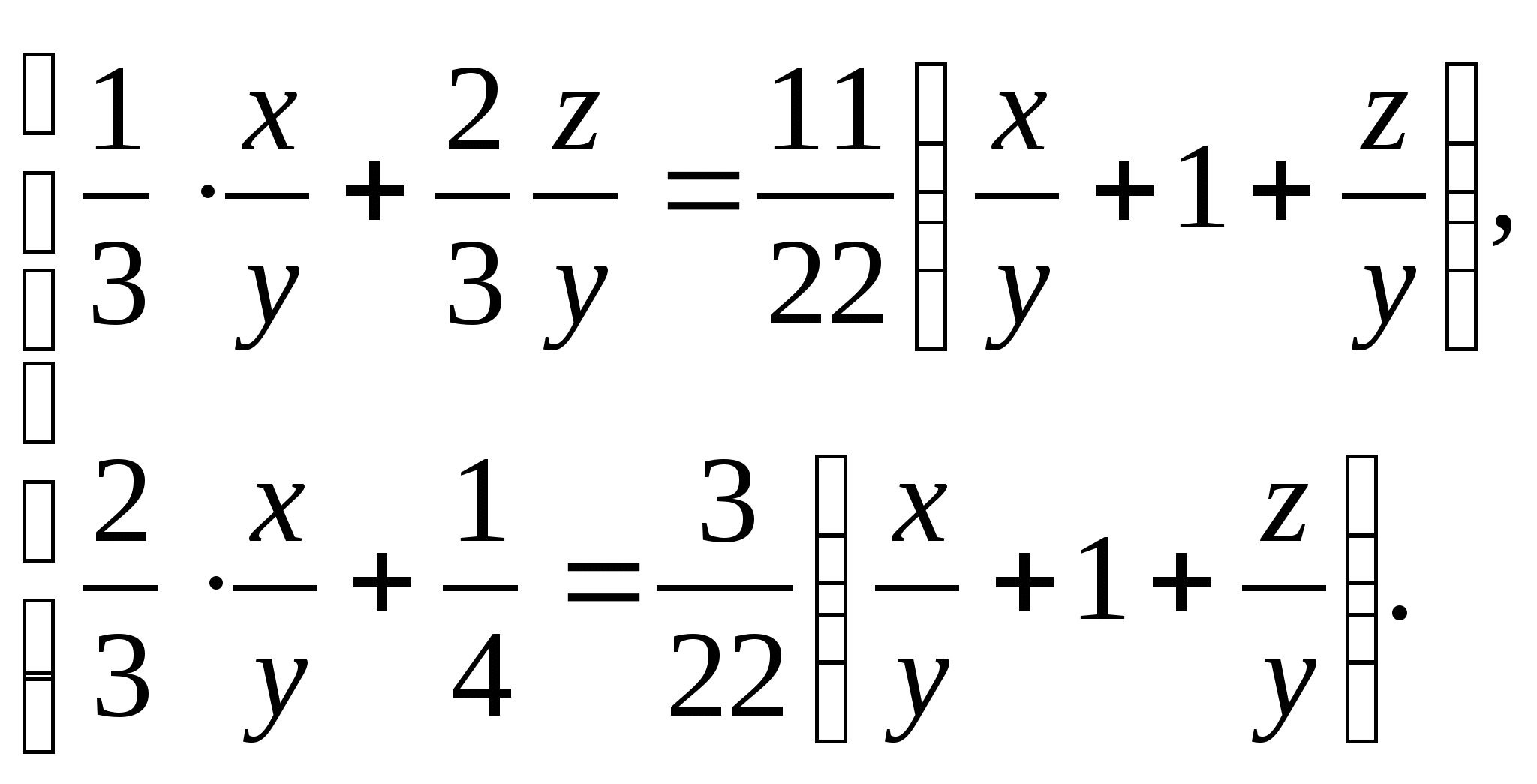
Теперь система имеет два уравнения и две переменных: 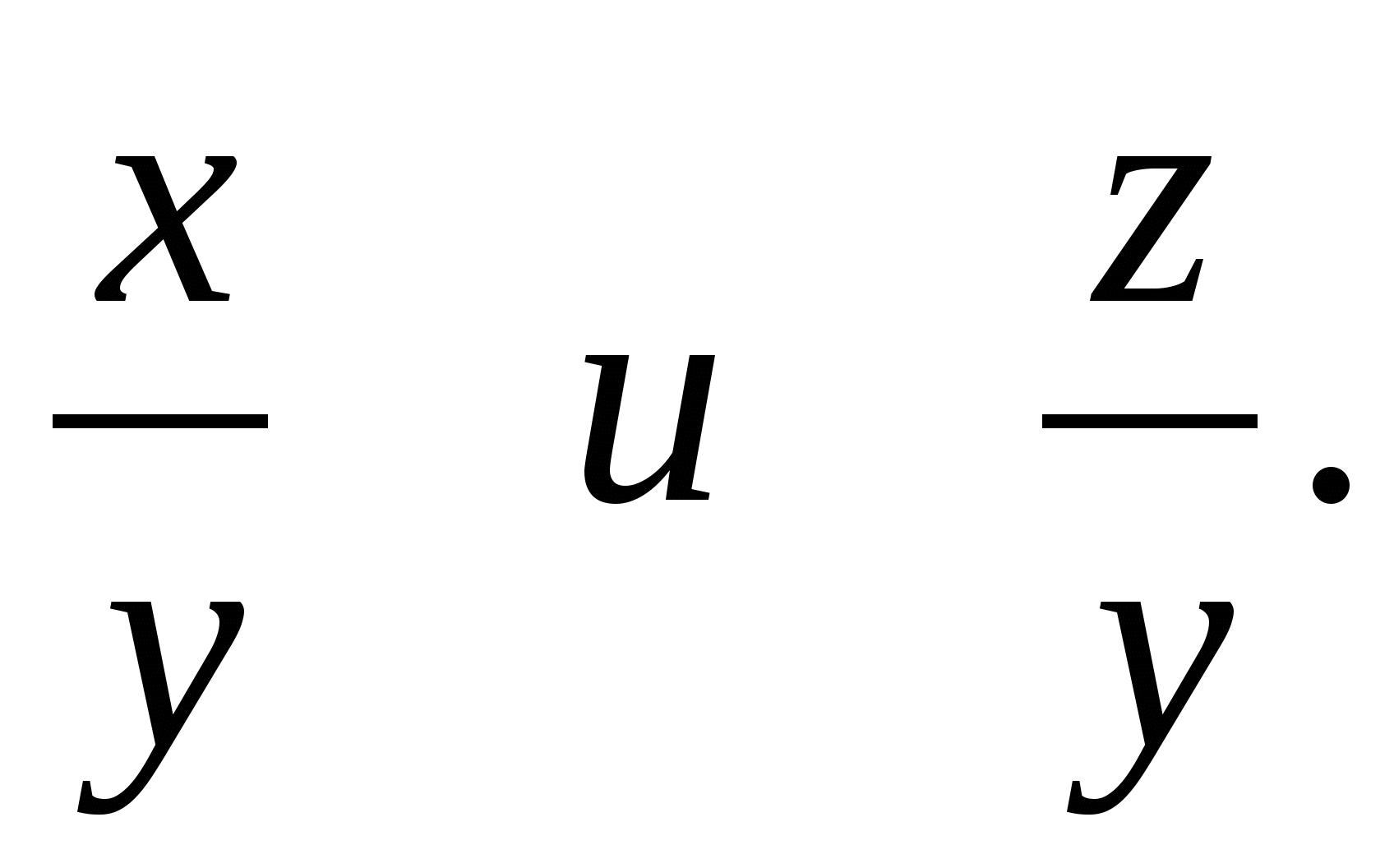Целесообразно для удобства записей ввести новые переменные: 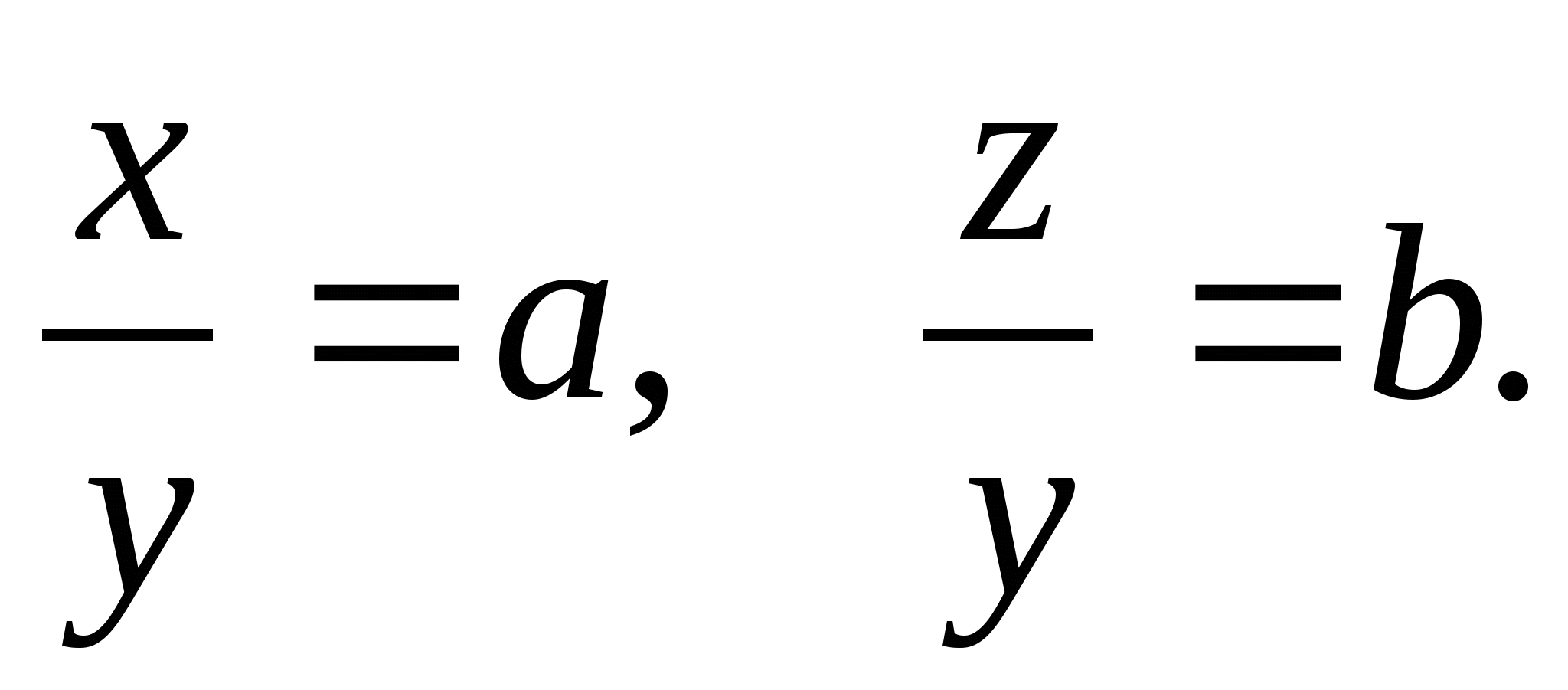Теперь система принимает вид:

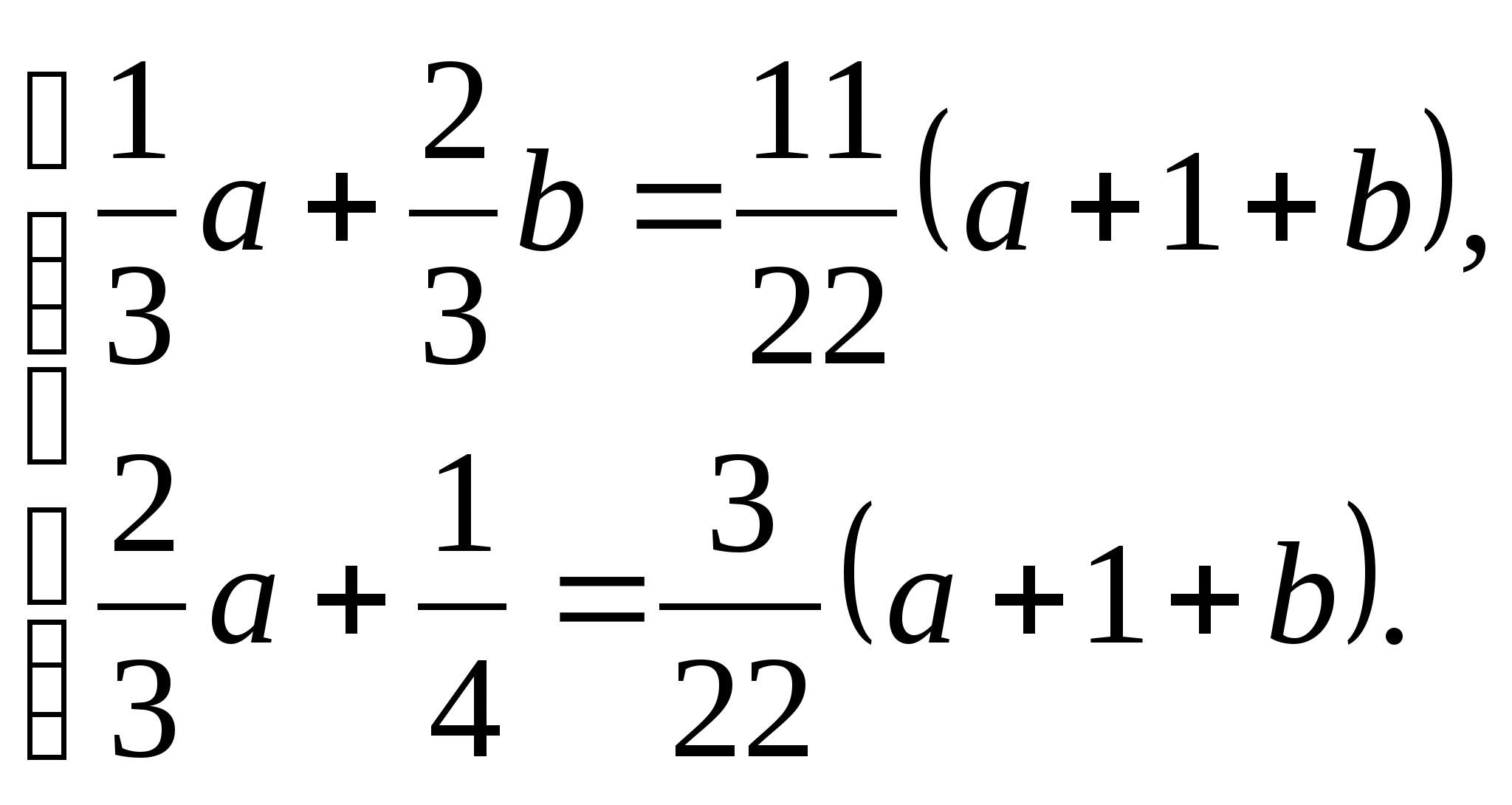
В результате решения системы получаем: 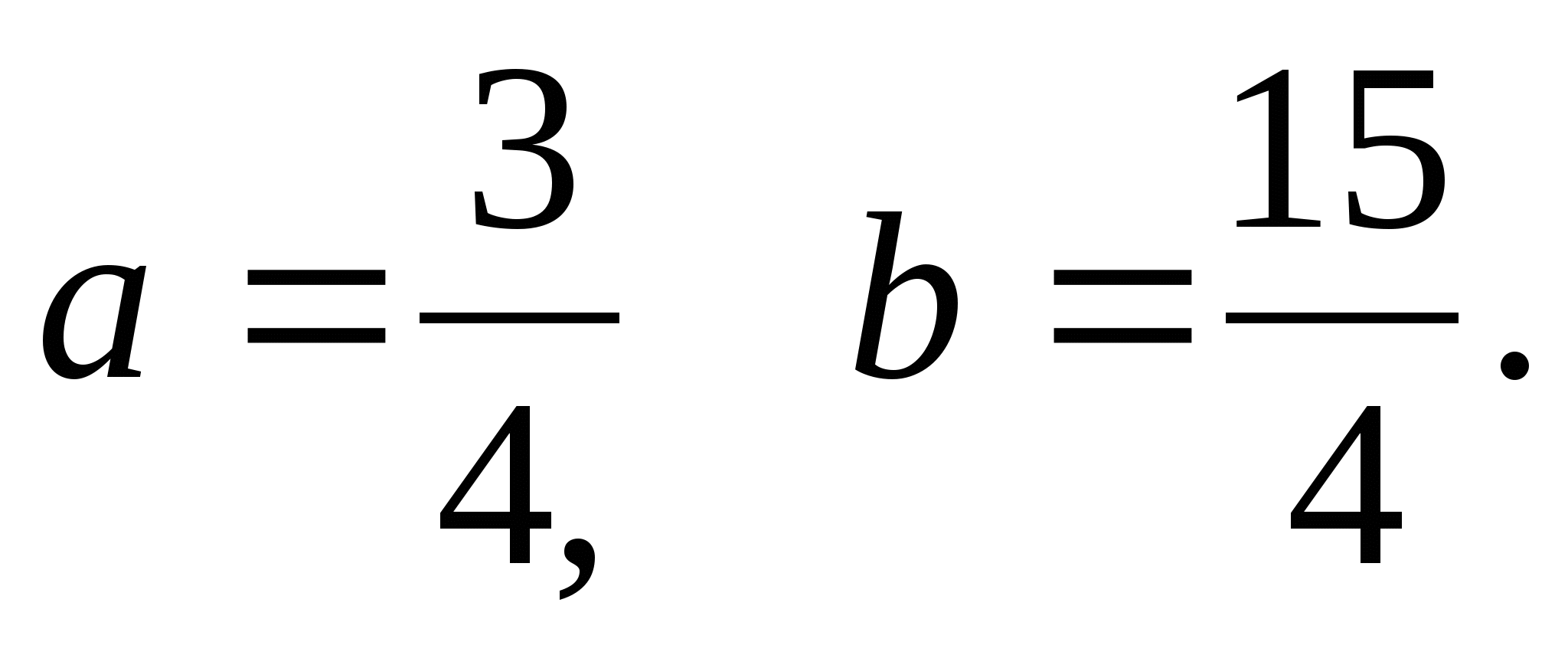это означает, что 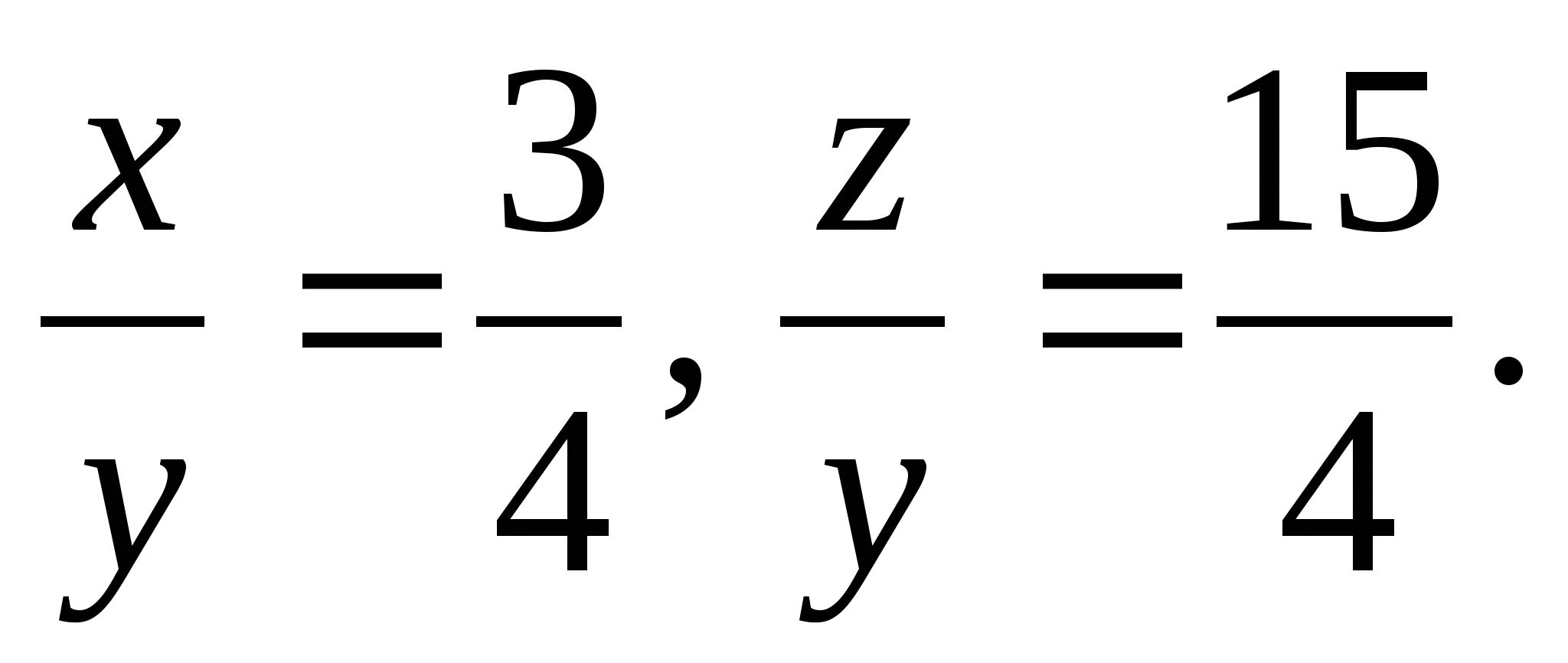следовательно, искомое отношение имеет вид: x:y:z=3:4:15.

Ответ:3:4:15.

Задача 3. Для консервирования 10 кг баклажан необходимо 0,5 л столового уксуса(10 % раствор уксусной кислоты). У хозяйки имеется уксусная эссенция (80 % раствор уксусной кислоты), из которой она готовит уксус, добавляя в нее воду. Сколько миллилитров уксусной эссенции понадобится хозяйке для консервирования 20 кг баклажан?

Решение.

Для консервирования 20кг баклажан понадобится 1л или 1000мл столового уксуса (10% раствор уксусной кислоты). Для получения его из х мл уксусной эссенции (80% раствор уксусной кислоты) необходимо добавить воду.

Составим уравнение, подсчитав количество уксусной кислоты слева от знака неравенства, и приравняем его к количеству уксусной кислоты справа от него. Получаем уравнение

Значит, для приготовления 500мл маринада понадобится 125мл уксусной эссенции (80% раствор уксусной кислоты).

Ответ:125мл.

Задача 4. Свежие абрикосы содержат 80 % воды по массе, а курага (сухие

абрикосы) - 12 % воды. Сколько понадобится килограммов свежих абрикосов, чтобы получить 10 кг кураги?

Решение.

При высыхании абрикос испаряется вода, количество сухого вещества не меняется.

Составим уравнение, подсчитав количество сухого вещества.

0,2х=8,8

х=44.

Ответ:44кг.

Задача 5. По рецепту засолки огурцов на каждые 10 л рассола необходимо добавить 1 л столового уксуса . У хозяйки имеется уксусная эссенция (80 % раствор уксусной кислоты), из которой она готовит уксус (10 % раствор уксусной кислоты), добавляя в нее воду. Сколько миллилитров уксусной эссенции понадобиться хозяйке для приготовления 5 л рассола?

Решение.

Для приготовления 5л рассола необходимо 0,5л или 500мл столового уксуса (10 % раствор уксусной кислоты). Для получения его из х мл уксусной эссенции (80% раствор уксусной кислоты), необходимо добавить воду.

Составим уравнение, подсчитав количество уксусной кислоты слева ознака неравенства, и приравняем его к количеству уксусной кислоты справа от него. Получаем уравнение:

Значит, для приготовления 5л рассола хозяйке понадобится 62,5муксусной эссенции (80% раствор уксусной кислоты).

Ответ:62,5.

Задача 6. Кислый маринад для консервирования овощей содержит 24% столового уксуса (10 % раствор уксусной кислоты). У хозяйки имеется уксусная эссенция (80 % раствор уксусной кислоты). Сколько процентов уксусной эссенции должно содержаться в аналогичном маринаде?

Решение:

Объем маринада принимаем за единицу (1ед.об).. Если кислый маринад содержит 24% столового уксуса (10 % раствор уксусной кислоты) это значит, что в 1 ед. об. маринада содержится 0,24 ед.об столового уксуса. Найдем, сколько миллилитров уксусной эссенции содержится в 0,24 ед.об. столового уксуса (или в 1ед.об. рассола).

вода

вода

вода

х г

+

Составим уравнение, подсчитав количество уксусной кислоты слева от знака неравенства, и приравняем его к количеству уксусной кислоты справа от него. Получаем уравнение:

0,8х=0,024 ;

х=0,03.

Так как в 1ед.об. рассола содержится 0,03ед.об. уксусной эссенции, то процентное ее содержание составляет 3%.

Ответ:3.

Заключение

В результате работы над проектом:

• была изучена литература и интернет-ресурсы по данной теме;

• собранная информация проанализирована и обработана;

• выбрано и изучено необходимое программное обеспечение;

• углублены и закреплены знания по теме;

• разработан сборник задач;

• подготовлен отчет в бумажном и электронном виде.

Выводы: в результате проведенной работы были изучены и расширены знания по данной теме, рассмотрены сложные задачи и их решения, разработан сборник задач по теме.

Список использованных источников

1. </ Интернет (www.yandex.ru/)

2. Журнал « Математика в школе»

3. Учебно-тренировочные тесты по новому плану ГИА под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова

4. Типовые экзаменационные варианты под редакцией А.Л. Семенова, И.В. Ященко

5. Учебники алгебры 7-11 кл. под редакцией Ш.А. Алимов и др.