7


  • Учителю
  • «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».

«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».

Автор публикации:
Дата публикации:
Краткое описание:
предварительный просмотр материала

Открытый урок по геометрии в 9 классе.

11.02.15г



Учитель: Кудзоева С.В.



Тема:

«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».



Цели урока:



Образовательная цель: закрепить формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности, научить учащихся применять указанные формулы в процессе решения задач;

Развивающая цель: учиться анализировать - устанавливать причинно-следственные связи; сравнивать; обобщать; выдвигать гипотезы;

Воспитательная цель: воспитание эстетического отношения к окружающей действительности, явлениям, культуре;

Оборудование: интерактивная доска, презентация MS Power Point;



Ход урока:

I Актуализация:

  1. Теоретический опрос.

  • Два ученика вызываются к доске для подготовки: а) формул радиусов вписанной в правильный многоугольник и описанной около правильного многоугольника окружностей, б) решения задач по карточке:

«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».

  • Найдите углы правильного двенадцатиугольника.

  • Угол правильного n-угольника равен 108º. Вычислите количество его сторон.

  • Сколько сторон имеет правильный вписанный многоугольник, если дуга описанной окружности, которую стягивает его сторона,

равна 45 º?



Фронтальный опрос (проводится в то время, пока у доски идет подготовка к доказательству теорем).

  • Какая формула используется для вычисления суммы углов выпуклого n-угольника?

  • Назовите формулу для вычисления угла правильного n-угольника?

  • Сформулируйте следствия из теорем о вписанной в правильный многоугольник и описанный около правильного многоугольника окружностях.

  • Что вы понимаете под словами центр правильного многоугольника?

  • Разгадать кроссворд, подготовленный ученицей.

  • формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности

Заслушать ответы, подготовленные у доски.

Ребята, а так ли уж важно изучать и знать сведения о правильных многоугольниках? В каких житейских ситуациях можно встретиться с правильными многоугольниками?(заслушать сообщение Плиевой Агунды о пчелиных сотах)

II Формирование умений и навыков:

Задача 1 Около правильного треугольника описана

окружность радиуса R.

Докажите, что R = 2r , где r - радиус

окружности, вписанной в этот треугольник.

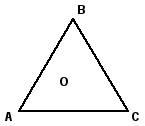
«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».



Дано: «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». АВС - правильный

«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».АВС вписан в окружность «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». (О;R)

«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».АВС описан около окружности «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». (О;r)

. Доказать: R = 2r.







Доказательство:

1 способ: свойство медианы треугольника.

Медианы треугольника пересекаются и точкой пересечения делятся в отношении 2:1, считая от вершины.

Имеем: «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». ; R = 2r.

2 способ: свойство биссектрисы угла треугольника (пропорциональность).

В «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». ВАД, АО - биссектриса, она делит сторону ВД на отрезки, пропорциональные двум прилежащим сторонам треугольника, то есть «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». ; «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». ; R = 2r.

3 способ: подобие треугольников.

«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». ВКО «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».ВДС, «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». В - общий. Используя свойство отрезков при подобии имеем: «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». ; «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». ; «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». ; R = 2r.

4 способ: свойство катета прямоугольного треугольника, лежащего против угла в 300.

«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».ВОК - прямоугольный, «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». ОВК=300;

ОК = «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». ОВ; ОВ = 2ОК; R = 2r.

5 способ: понятие синуса угла прямоугольного треугольника.

Дайте определение синуса острого угла прямоугольного треугольника.

sin «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». ВОК =«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».; sin 300 =«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».; «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». ; R = 2r.

6 способ: аналитический.

«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».АВС - правильный. Выразим сторону треугольника через радиус вписанной и описанной окружности относительно треугольника.

a3= 2R sin600; a3=2r tg 600;2R sin600= 2r tg 600.

R«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».; R = 2r.



Задача №2:

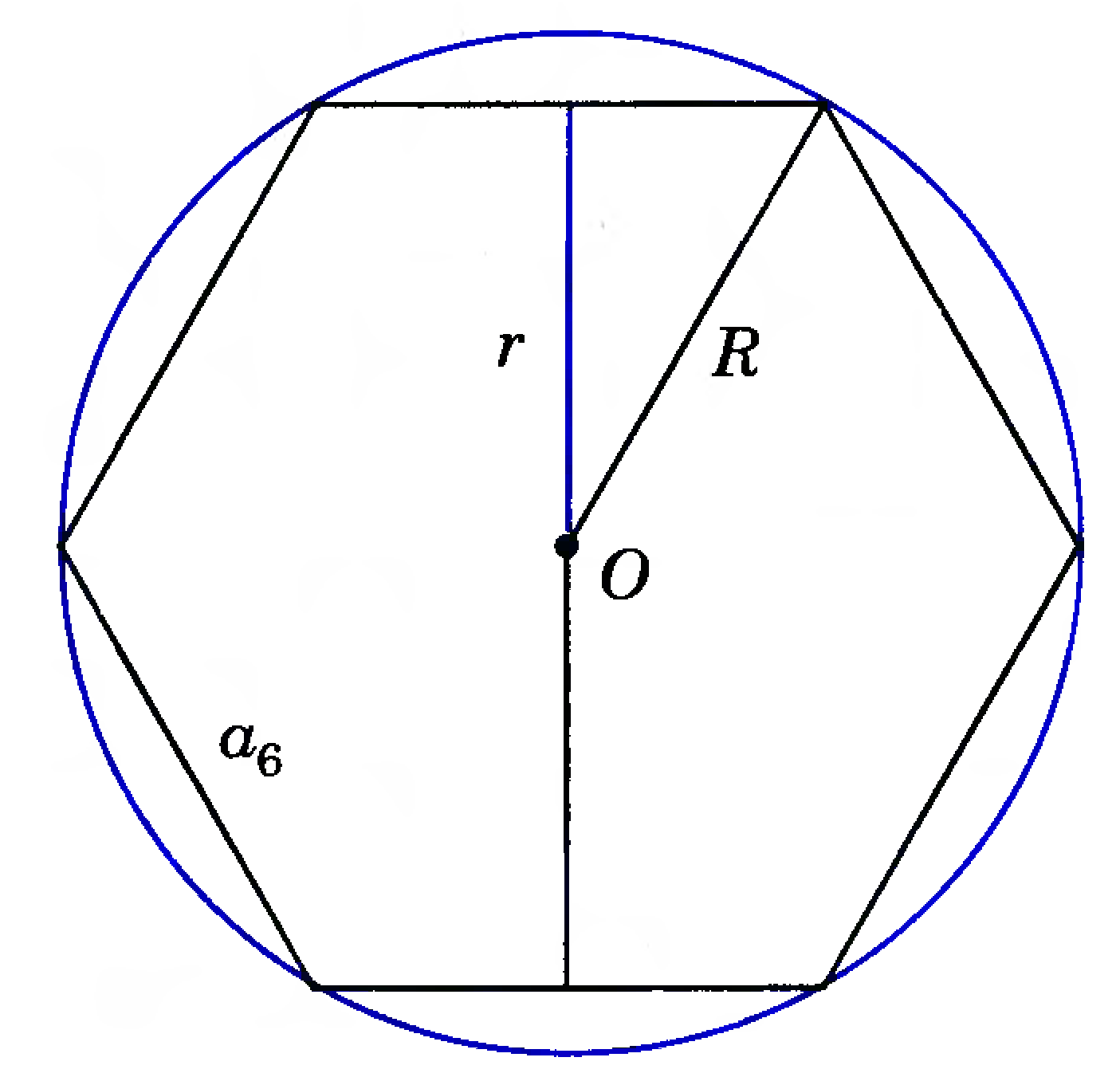На рисунке изображен правильный шестиугольник, вписанный в окружность радиуса R. Пусть «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». - сторона правильного шестиугольника, r - радиус вписанной окружности, P - периметр, S - площадь.

«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».Найдите значение «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». , R,P и S, если «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». см.

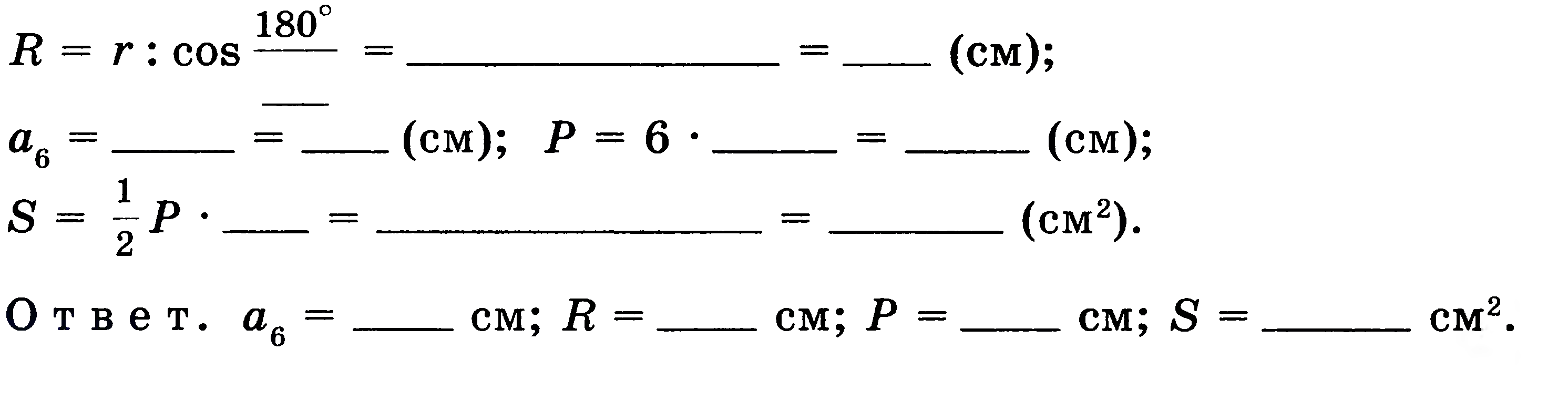
Решение. По условию «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». см, поэтому

«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».

Задача №3 (№1089 из учебника):

  • Квадрат вписан в окружность. Что нужно знать для определения стороны квадрата? (Для определения стороны квадрата нужно знать радиус описанной около него окружности).

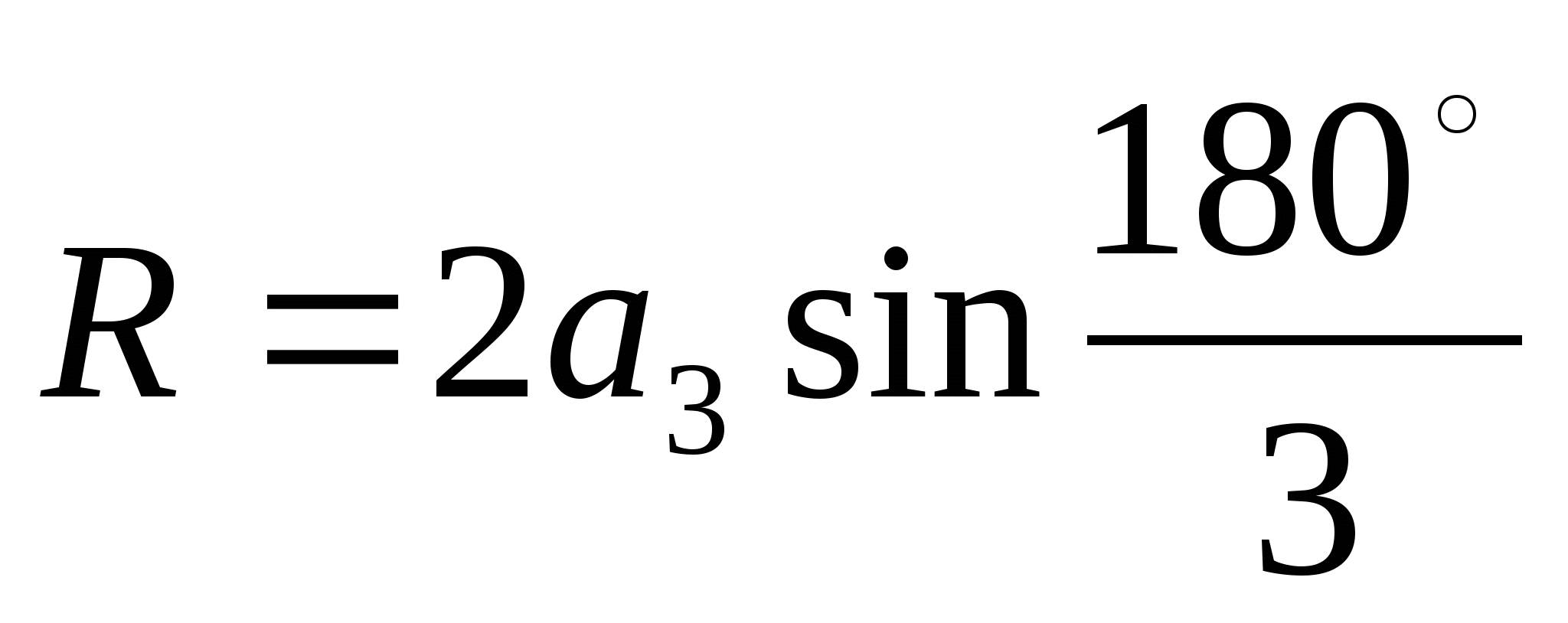  • Как по известному периметру треугольника можно вычислить радиус описанной около него окружности? (Найдем сторону треугольника, а затем используем формулу «Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач». ).

  • Решение задачи:

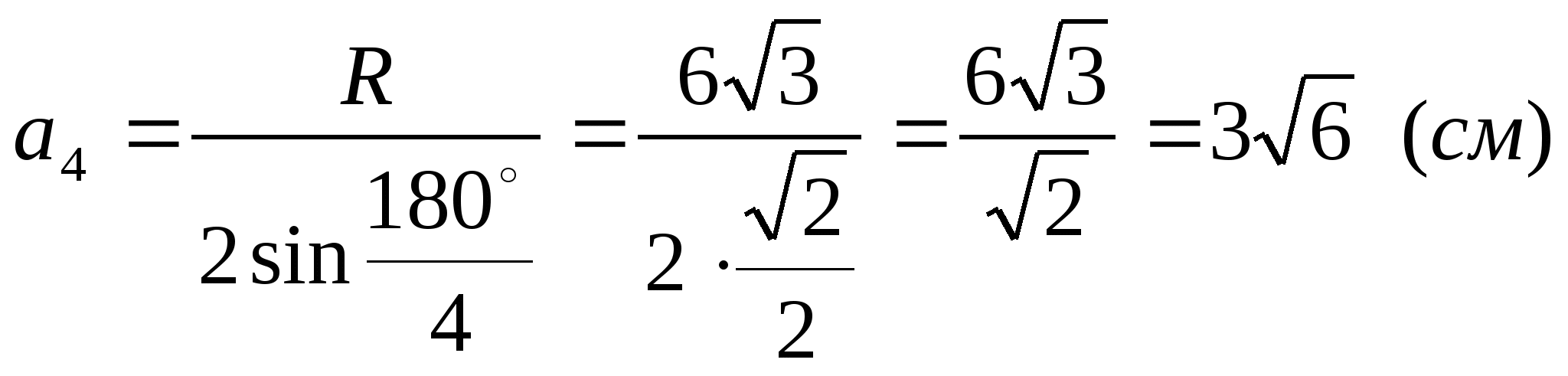
«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».

«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».

«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной и описанной окружности. Решение задач».

IV Подведение итогов урока.

V Домашнее задание. 1087 (3,5); 1088.

VI Оценка знаний (комментирование выставляемых оценок).



⇧
⇩
скачать материал


 
 
X

Чтобы скачать данный файл, порекомендуйте его своим друзьям в любой соц. сети.

После этого кнопка ЗАГРУЗКИ станет активной!

Кнопки рекомендации:

загрузить материал