Рабочая программа по алгебре 8 класс по учебнику Мерзляк

Пояснительная записка

Настоящая рабочая программа по алгебре для 8 класса составлена на основе:

- федерального компонента Государственного образовательного стандарта, утвержденное приказом Минобразования РФ №1089 от 05.03.2004 г «Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного) общего образования»;

- основной образовательной программы основного общего образования и основной образовательной программы среднего общего образования МБОУ «Аршановская СШ»;

- учебного плана МБОУ «Аршановская СШ», с учетом примерной программы основного общего образования по математике (А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. - М..: Вентана - Граф, 2013) и отражает основные моменты Положения о рабочей программе учебного предмета, элективного учебного предмета в МБОУ «Аршановская СШ».

Изучение математики на ступени основного общего образования направлено на достижение следующих целей:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

Задачи:

• развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;

• овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;

• изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;

• получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;

• развить логическое мышление и речь - умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;

• сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

Общая характеристика учебного предмета

Представление учащихся о взаимосвязи математики и окружающего мира достигается сочетанием теоретического и современных прикладных аспектов школьного курса математики. Этому способствует и тот факт, что в программе и учебных пособиях отражены внутрепредметные и межпредметные связи. На уроках математики, как правило, готовиться весь аппарат, необходимый для изучения смежных предметов на достаточно высоком уровне. Уже в IV-Vклассах вводятся простейшие буквенные формулы, в VIклассе - отрицательные числа. Приступая в IXклассе к изучению механики, учащиеся знают уравнение равномерного движения, знакомы с графиками, умеют решать задачи на движение графическим и аналитическим способами, владеют необходимыми сведениями из векторной алгебры.

Требования к уровню подготовки учащихся

Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

• алгебраической дроби; основном свойстве дроби;

• правилах действий с алгебраическими дробями;

• степенях с целыми показателями и их свойствах;

• стандартном виде числа;

• функциях 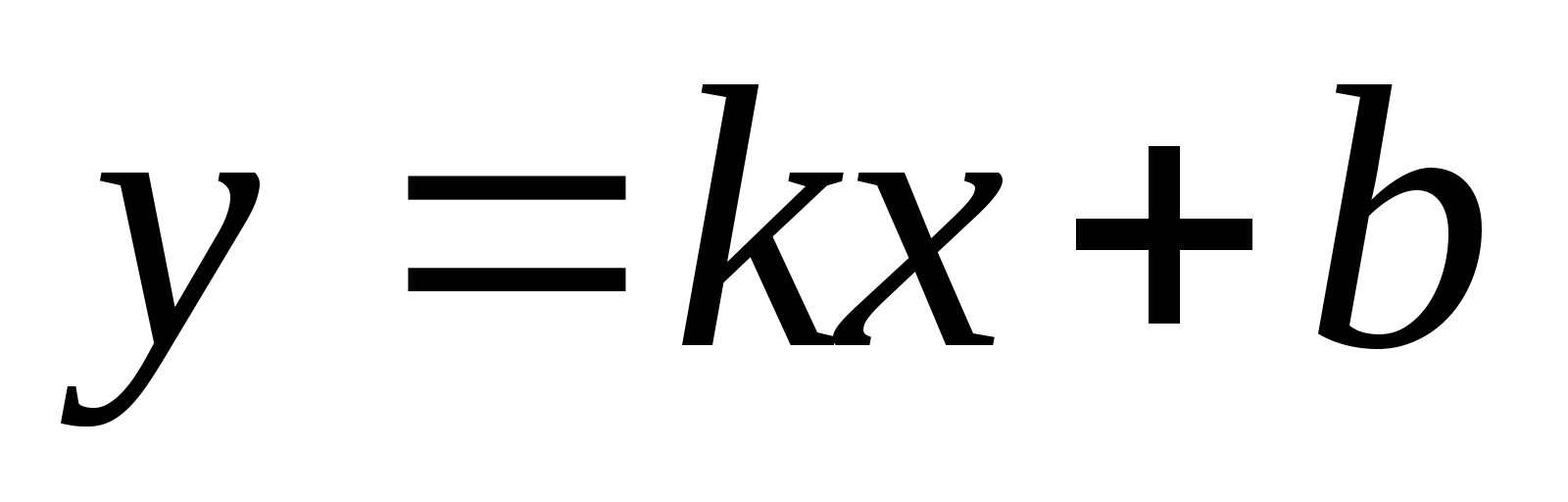, , 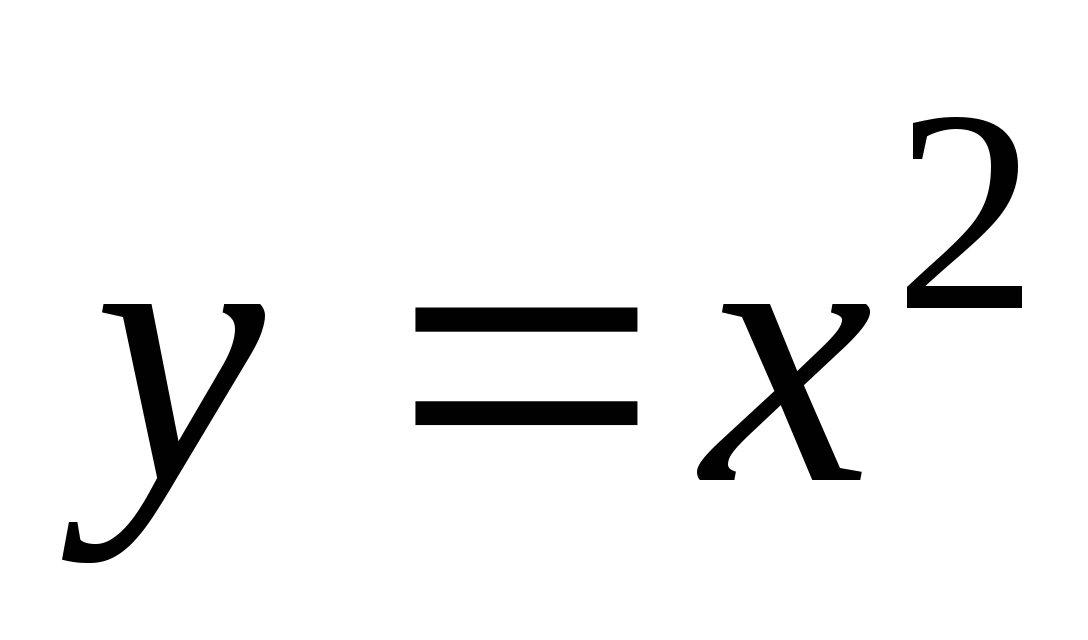, 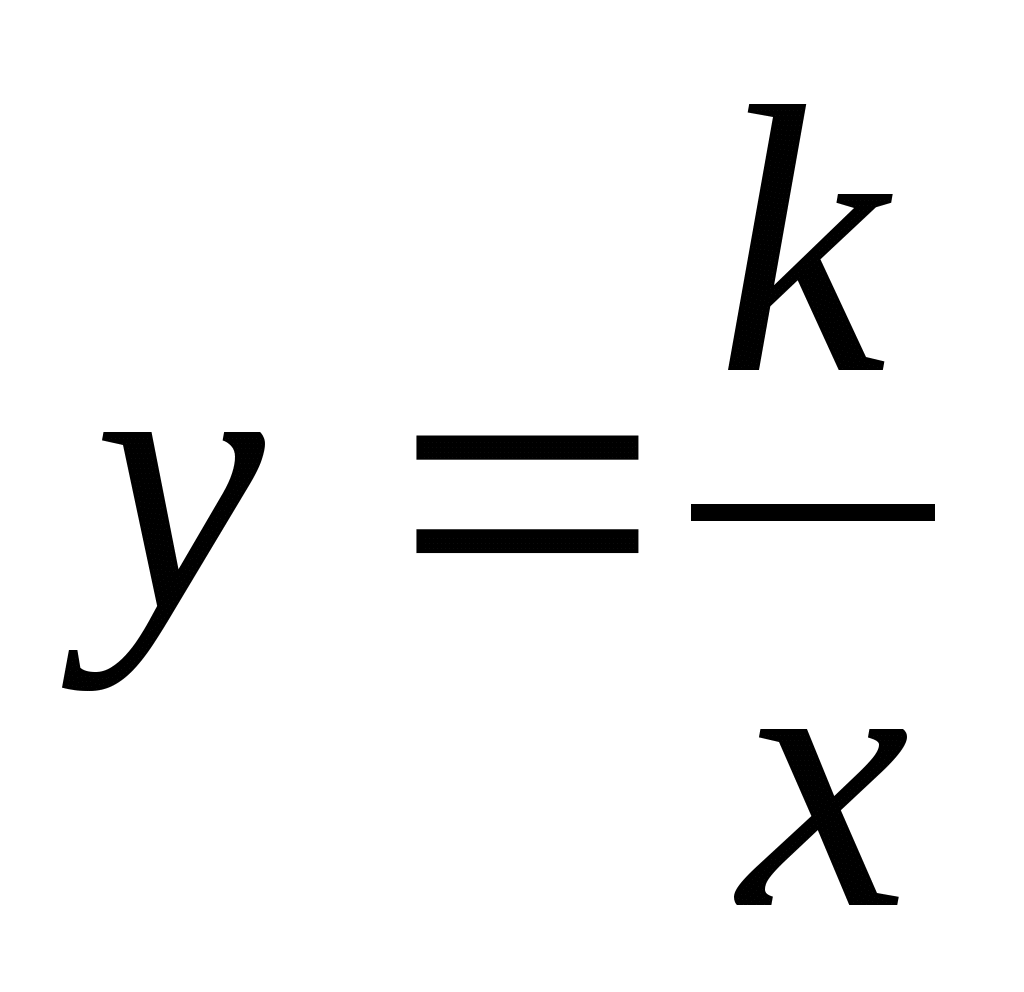их свойствах и графиках;

• понятии квадратного корня и арифметического квадратного корня;

• свойствах арифметических квадратных корней;

• функции 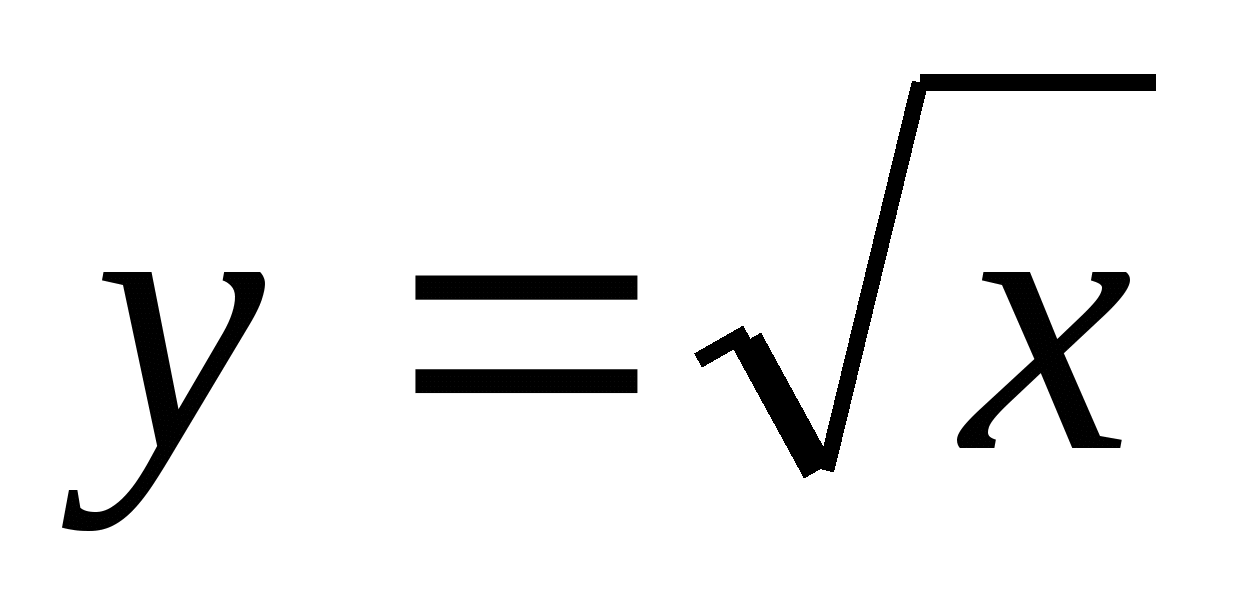, её свойствах и графике;

• формуле для корней квадратного уравнения;

• теореме Виета для приведённого и общего квадратного уравнения;

• основных методах решения целых рациональных уравнений: методе разложения на множители и методе замены неизвестной;

• методе решения дробных рациональных уравнений;

• основных методах решения систем рациональных уравнений.

• Сокращать алгебраические дроби;

• выполнять арифметические действия с алгебраическими дробями;

• использовать свойства степеней с целыми показателями при решении задач;

• записывать числа в стандартном виде;

• выполнять тождественные преобразования рациональных выражений;

• строить графики функций 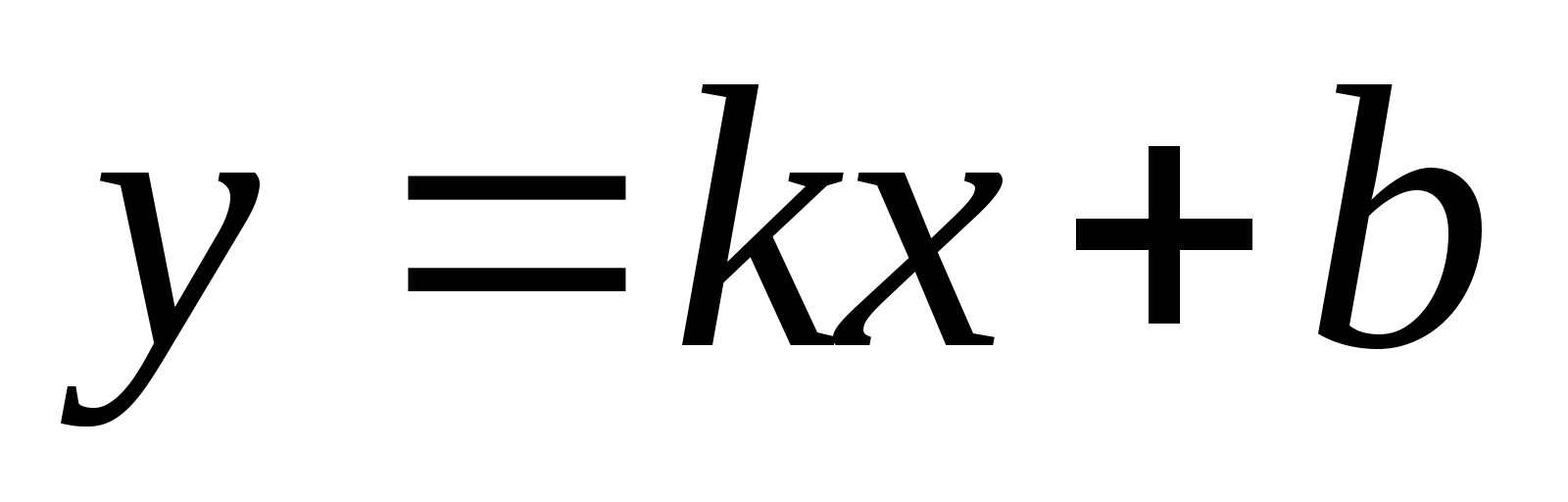, , 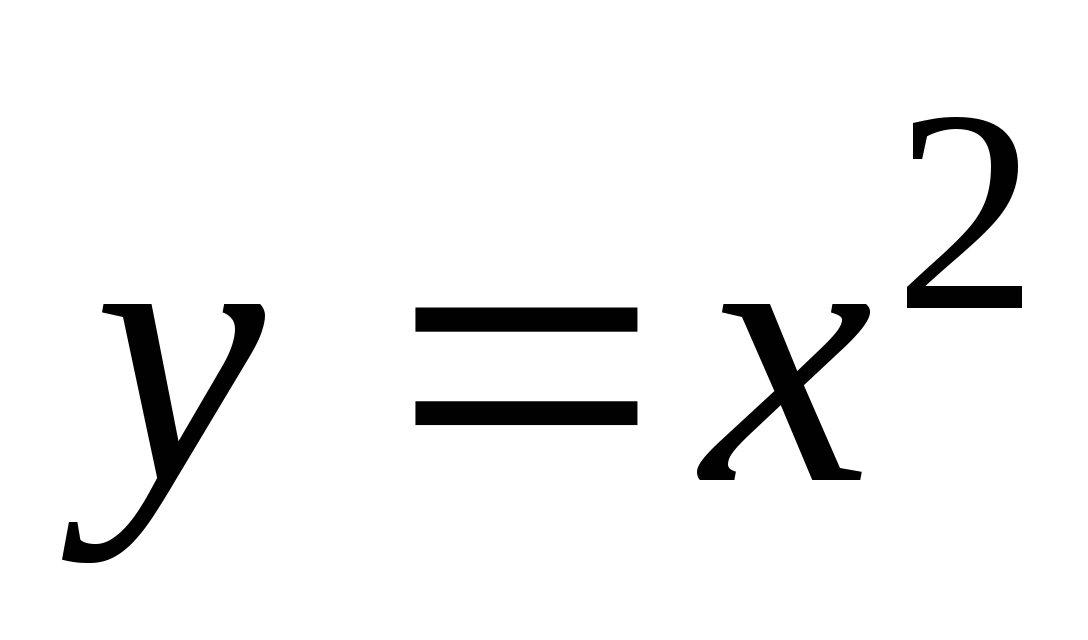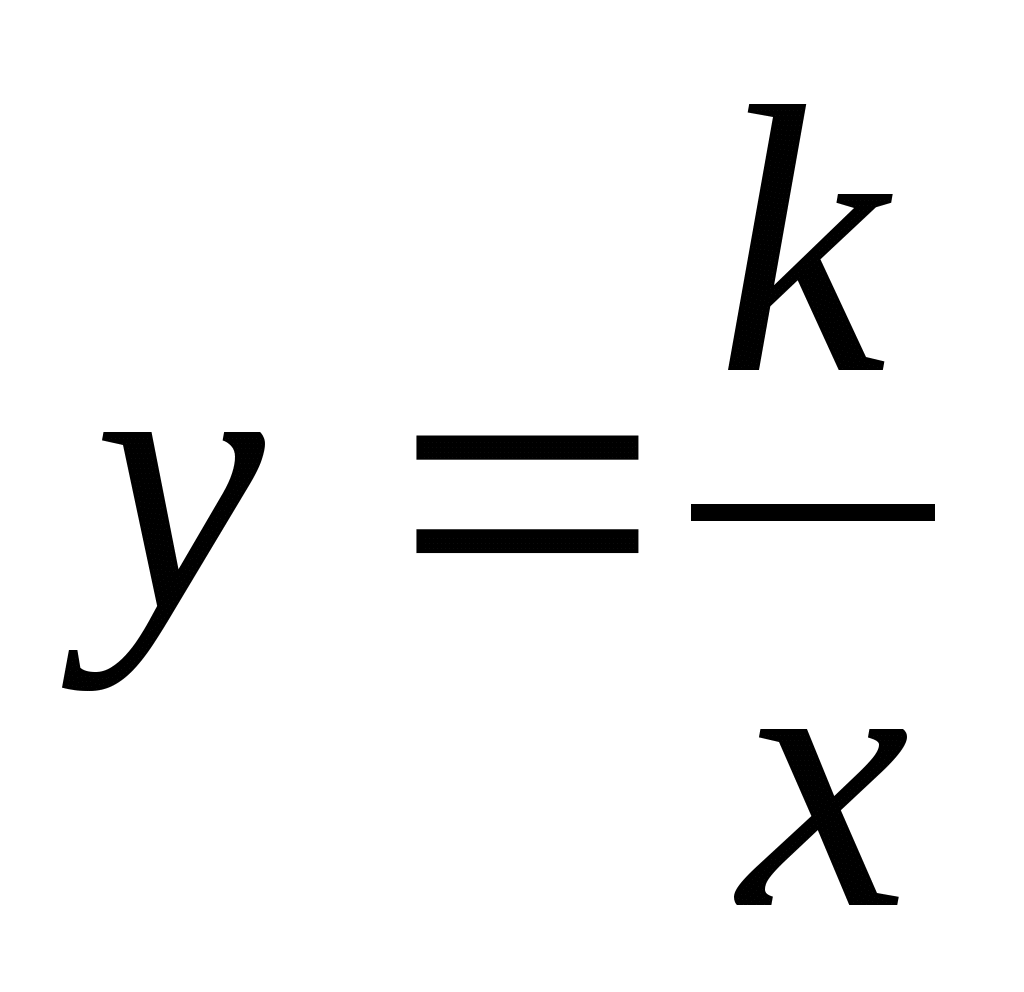и использовать их свойства при решении задач;

• вычислять арифметические квадратные корни;

• применять свойства арифметических квадратных корней при решении задач;

• строить график функции 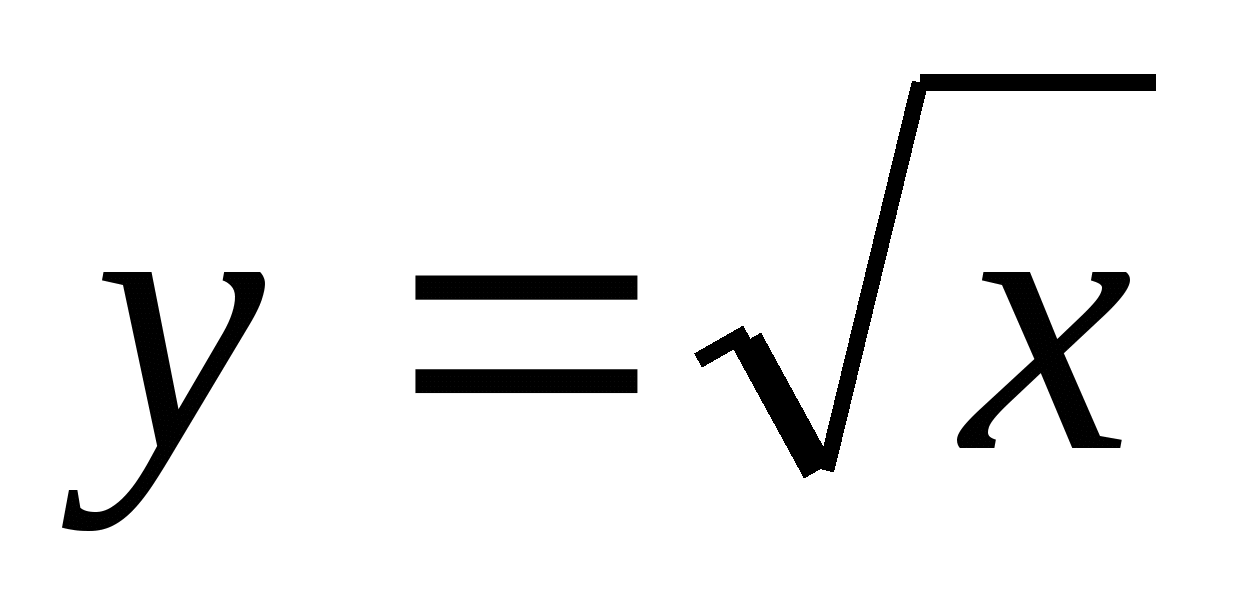и использовать его свойства при решении задач;

• решать квадратные уравнения;

• применять теорему Виета при решении задач;

• решать целые рациональные уравнения методом разложения на множители и методом замены неизвестной;

• решать дробные уравнения;

• решать системы рациональных уравнений;

• решать текстовые задачи с помощью квадратных и рациональных уравнений и их систем;

• находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

Межпредметные связи.

Достаточный уровень систематизации знаний учащихся может быть достигнут только пи осуществлении межпредметных связей, которые, кроме того способствуют формированию у школьников целостной научной картины мира.

На основе знаний по математике в первую очередь формируются общепредметные расчетно-измерительные умения. Преемственные связи с курсами естественнонаучного цикла раскрывают практическое применение математических умений и навыков. Это способствует формированию у учащихся целостного, научного мировоззрения.

Содержание тем учебного предмета

Алгебраические дроби.

Рациональная дробь. Основное свойство дроби, сокращение дробей. Сложение, вычитание, умножение и деление дробей. Преобразование рациональных выражений. Функция и её график.

Квадратные корни. Действительные числа.

Понятие об иррациональном числе. Общие сведения о действительных числах. Квадратный корень, приближённое значение квадратного корня. Свойства квадратных корней. преобразования выражений, содержащих квадратные корни. Функция и её график. Степень с целым показателем и её свойства. Стандартный вид числа. Запись приближенных значений. Действия над приближенными значениями.

Квадратные уравнения.

Квадратное уравнение. Формулы корней квадратного уравнения. Теорема Виета. Решение рациональных уравнений. Решение задач, приводящих к квадратным и рациональным уравнениям.

Неравенства.

Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Применение свойств неравенств к оценке значения выражения. Линейное неравенство с одной переменной. Система линейных неравенств с одной переменной.

Учебно - методический комплекс:

1. Мордкович А.Г. Алгебра (в 2-х частях). Ч. 1: Учебник (8 класс), Ч. 2: Задачник (8 класс). - М. Мнемозина, 2010;

2. Контрольно-измерительные материалы. Алгебра: 8 класс/ Сост. Л.Ю. Бабошкина. - М.: ВАКО, 2010

Календарно-тематическое планирование

Лист корректировки рабочей программы по математике

Иптешевой Екатерины Николаевны

Тема

урока

Дата проведения урока по плану

Причина корректировки

Дата проведения

Подпись зам.директора по УВР/

директора ОУ

12