Урок и презентация по математике для 10 класса по теме «Решение простейших тригонометрических уравнений»

МОУ Елшанская средняя общеобразовательная школа

Конспект урока

по алгебре и началам анализа

в 10 классе

по теме «Решение простейших тригонометрических уравнений»

Учитель математики

первой квалификационной категории

Антипова Любовь Владимировна

2013 г.

Цели урока:

• Выявить уровень овладения учащимися комплексом знаний свойств функции у=cosx (область определения, множество значений, четность, периодичность, промежутки монотонности) и умений вычислять значения обратных тригонометрических функций;

• Вывести формулу решения простейшего тригонометрического уравнения cosx=а, сформировать у учащихся первичные умения и навыки их решения;

• Развивать:

• умение обобщать, абстрагировать и конкретизировать знания при решении уравнений;

• навыки самоконтроля при выполнении самостоятельной работы.

• Способствовать воспитанию воли и настойчивости для достижения конечных результатов.

План урока:

1. Организационный момент. (2 минуты)

2. Актуализация знаний, умений, навыков. (8 минут)

3. Изучение нового материала. (10 минут)

4. Закрепление учебного материала. (8 минут)

5. Информация о домашнем задании. (1 минуты)

6. Подведение итогов урока. (1 минуты)

Оборудование:

Мультимедийный проектор, карточки для проведения рефлексии, оценочные листы, карточки с разноуровневым заданием, таблицы по тригонометрии:

а) значения тригонометрических функций,

б) основные формулы тригонометрии.

Используемые методы обучения:

Методы организации учебно-познавательной деятельности: наглядные, практические, квазиисследовательские. Методы стимулирования и мотивации учебно-познавательной деятельности: учебная дискуссия, эмоциональное воздействие. Методы контроля: письменный, самопроверка.

Ход урока:

1. Организационный момент.

Сегодня на урок я пришла с настроением, которое у меня ассоциируется с солнышком. Покажите, пожалуйста, ваше настроение: если радостное и спокойное, то покажите солнце, с тревогой и печалью - солнце за тучей, пасмурное, хочется остаться дома - туча. Я надеюсь, что встреча с математикой ваше хорошее настроение укрепит.

• Тема урока «Решение простейших тригонометрических уравнений». Цель занятия - выявить уровень овладения вами комплексом знаний по свойствам функции у=cosx (область определения, множество значений, четность, периодичность, промежутки монотонности) и умений вычислять значения обратных тригонометрических функций;

Мы познакомимся с тригонометрическими уравнениями вида cosx=а, выведем формулу корней этого уравнения. Я верю вам интересно попробовать свои силы и доказать себе и другим, что вы можете подняться на новую ступеньку в своих знаниях.

Оценочный лист

Ф.И.

Задания

Уровень

Баллы

1. Вычисления значений обратных тригонометрических величин

Знать значения тригонометрических функций

2. Устная работа по тригонометрическим уравнениям

Знать свойства функции

у= соs a

3. Решение уравнений

Уметь решать уравнения

4. Самостоятельная работа

Уметь решать уравнения

5. Активность

Быть активным

Итоговый результат

«3» - 15-20 баллов,

«4» - 20-24 баллов,

«5» - 25-27 баллов2. Актуализация знаний, умений, навыков.

В: Что называется арккосинусом числа а?

О: Арккосинусом числа а называется такое число из отрезка[0;], косинус которого равен а.

В: Для каких чисел определён арккосинус?

О: Арккосинус определён для а [-1;1].

В: Чему равен arcсos(-а)?

О: arcсos(-а)= - arcсos а

Устные задания:

1. Верно ли, что:

arccos=, arccos=-,

Вычислить значения обратных тригонометрических величин.

а) arccos

б)

в) arccos 1

г) arccos (-1)

д) arccos 0

е)

ж) arccos (-)

з) arcсos

и) 2arccos

к)

л)arccos-

м) arccos (-1)+ arccos 0

н) arccos

о)

п) tg()

р) ctg( arccos 0)

Ответы:

а)

б)

в) 0

г)

д)

е)-

ж)

з)

и) 2

к)

л)

м)

н)

о)

п)

р) 0

3.На единичной окружности отметьте точки, соответствующие решениям уравнений: cos t=0, cos t=1, cos t=-1. Запишите общий вид решений.

4.Назовите:

1) Область определения функции;

2) Множество значений функции;

3) Периодичность;

4) Чётность;

5) Промежутки возрастания и убывания;

2. Изучение нового материала.

Опр. Простейшими тригонометрическими уравнениями называют уравнения вида cos x=a, sin x=a, tg x= a, ctg x=a. В этих уравнениях переменная находится под знаком тригонометрической функции, а - данное число.

Сегодня мы научимся решать уравнения вида cos x=a.

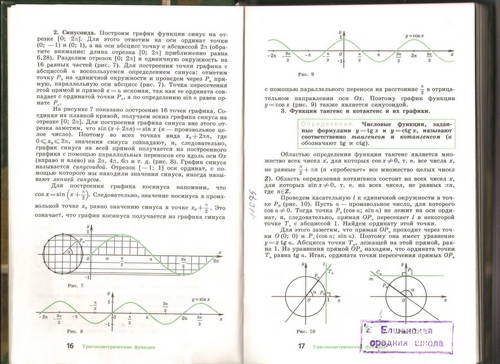
1. Рассмотрим графики функций в одной системе координат у=cos x и у=а.

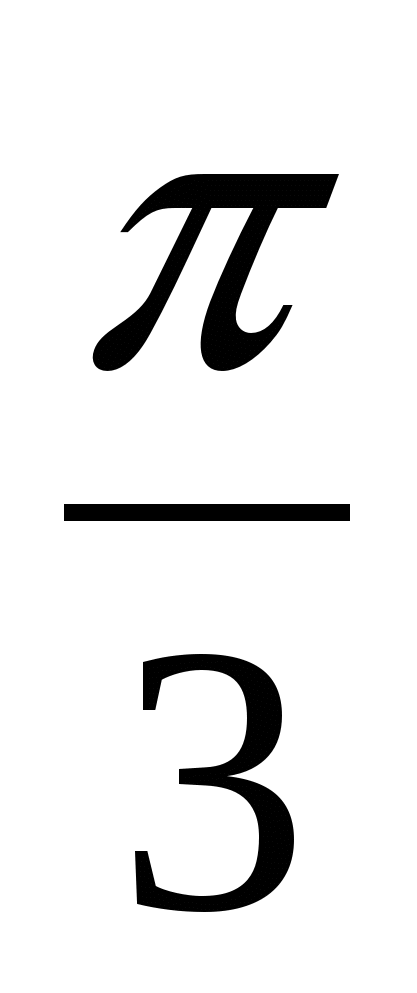
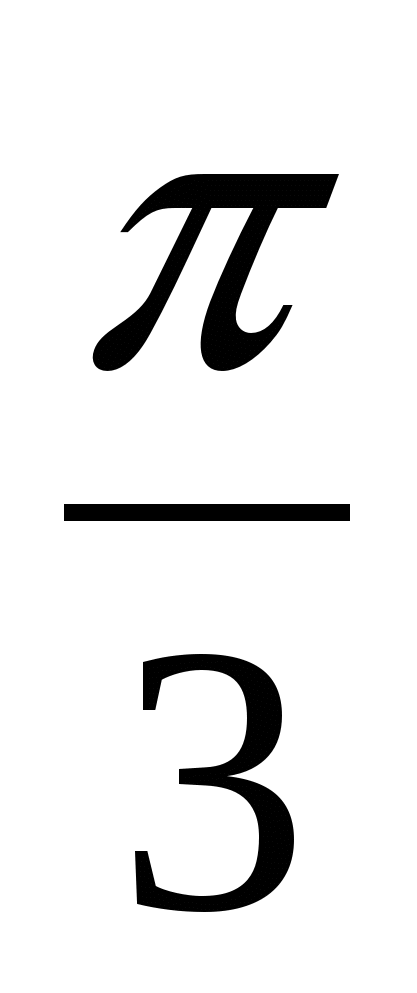
1.|а| >1, т.е. а>1 или а<1, то :

Сделайте вывод самостоятельно.

О: уравнение cos x=a не имеет решений, если |а| >1;

2. .|а|<1, тогда:

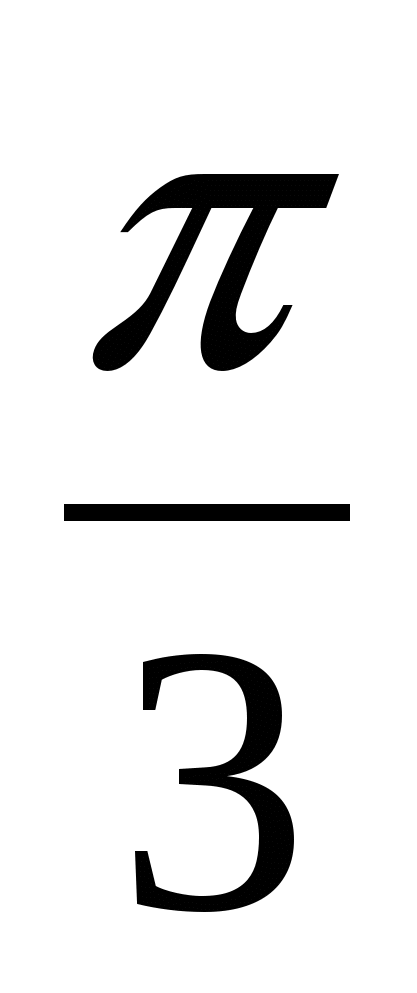
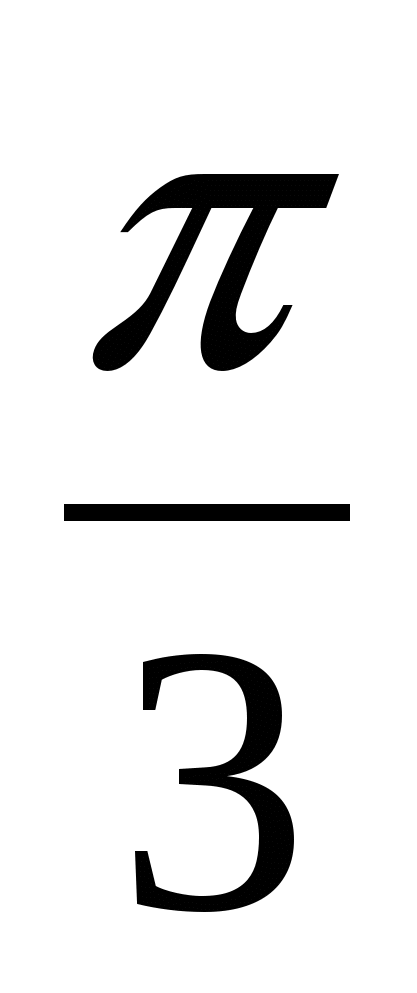
То уравнение cos x=a на отрезке [0;] имеет единственный корень, который называется arcсos а, т.к. функция на этом промежутке убывает и принимает все значения от -1 до 1. Косинус - чётная функция, значит на отрезке [-;0] уравнение имеет в точности одно решение - arcсos а. Значит на отрезке длиной 2 уравнение cos x=a имеет два корня. Как их записать одной формулой?

х= arcсos а..

Как записать все решения этого уравнения?

х=arcсos а+ 2n, n

так как функция периодическая, все остальные решения отличаются на 2n.

Итак, уравнение cos x=a имеет множество корней, которые записывают формулой вида: х=arcсos а+ 2n, , n

А уравнения : cos t=0, cos t=1, cos t=-1 имеют частные решения:

3. Закрепление.

Решить уравнения:

1) cos x =, x= arcсos+2n, n, x=;

2) cos x=, x= arcсos+2n, n;

3) cos x= -2.4, корней нет.

Закончите решение уравнения:

1) 2 cos x =

cos x =

x = arcсos+2n, n,

x =

2) cos 4 x = 0

4x =

4x =

x =

Заполните пропуски в решении уравнения:

cos x - 1 = 0

cos x=

cos x =

x = arcсos +2n, n,

x = +2n, n,

Найдите ошибку в решении уравнения:

1) cos x = -

x = arcсos (- )+ n, n,

x =

Разноуровневая самостоятельная работа.

Задания

I уровень

Ответы

1

2

3

4

cos x = -1

, n,

не имеет решений

2 cos x = 1

не имеет решений

cos x =1,1

не имеет решений

Задания

II уровень

Ответы

1

2

3

4

2cos x -1 =0

, n,

не имеет решений

2 cos 2x =-

не имеет решений

cos x =1,8

не имеет решений

Задания

III уровень

Ответы

1

2

3

4

cos x =

, n,

не имеет решений

cos(- x) = 1

не имеет решений

cos x =

не имеет решений

Проверка работы осуществляется с помощью готовых ответов на доске (взаимопроверка). Поставьте в тетради на полях оценку карандашом по следующим критериям:

«3» - 15-20 баллов,

«4» - 20-24 баллов,«5» - 25-27 баллов

Итоги урока:

1. Назовите формулу корней уравнения cos x=a.

2. Перечислите частные случаи.

Вы знаете кто является основателем современной тригонометрии?

Многие понятия и факты из тригонометрии были известны 2 000 лет назад. А вот современный вид тригонометрии придал крупнейший математик 18 столетия Леонард Эйлер(1707-1783). Швейцарец по происхождению, долгие годы работал в России и являлся членом Петербургской Академии наук. Он ввёл определения тригонометрических функций, получил формулы приведения, стал рассматривать функции произвольного угла.

В: Будьте добры, покажите, пожалуйста, ваше настроение в конце нашего урока.

Поставьте себе оценку за урок

Домашнее задание: п.9, стр.69-71,

На «3» - №137б,142б,г

На «4» и «5» №144в, 145а, 146а