Урок математики в 8 классе по теме «Решение текстовых задач на смеси и сплавы»

Тема:_____________________________________________________________

1 способ Табличный способ решения задач на смеси и сплавы

Задача Сколько граммов проявляющей эмульсии нужно добавить к 180 г смеси краски для волос, содержащей 25% красящей основы, чтобы получить смесь, концентрация которой равна 20%?

Решение:

Наименование веществ, растворов, смесей, сплавов

% содержание меди (доля содержания вещества)

Масса раствора (смеси, сплава)

Масса вещества

Ответ:

2 способ Решение задач с помощью модели-схемы

Задача Сколько граммов проявляющей эмульсии нужно добавить к 180 г смеси краски для волос, содержащей 25% красящей основы, чтобы получить смесь, концентрация которой равна 20%?

1. Над каждым прямоугольником («маленьким») указываем соответствующие компоненты смеси.

2. Внутри прямоугольников вписываем процентное содержание (или часть) соответствующего компонента. Понятно, что если раствор состоит из двух компонентов, то достаточно указать процентное содержание одного из них. В этом случае процентное содержание второго компонента равно разности 100% и процентного содержания первого.

3. Под прямоугольником записываем массу (или объем) соответствующего раствора (или компонента).

+

=

Решение:

Ответ:_____________

3 способ Старинный способ решения задач на смеси и сплавы (диагональная схема, «метод рыбки»)

Теория метода.

М₁ - масса первого раствора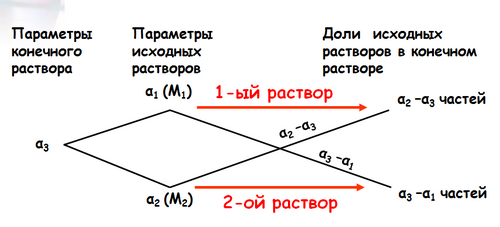

α₁ концентрация первого раствора

М₂ - масса второго раствора

α₂ концентрация второго раствора

М₁+ М₂ - масса конечного раствора

α₃ - концентрация конечного раствора

α₁ <����������_���������������������_{�������}

�������_{������}��������������_{�����}��������_�������������������������������������������

���_{������}��������������_{�����}��������_��������������������������������������������

�������_{������}���������������_{�����}���������_{�����}������_������������������������������������

���гой стороны m₃ = m₁+ m₂, получаем

α₃ (М₁+М₂) = α₁ М₁ + α₂ М₂;

α₃ М₁ + α₃ М₂ = α₁ М₁ + α₂ М₂;

α₃ М₁ - α₁ М₁ = α₂ М₂ - α₃ М₂;

М₁( α₃ - α₁) = М₂( α₂ - α₃);

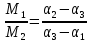
Параметры конечного раствора

Параметры исходных растворов

Доли исходных растворов в конечном растворе

Решение:

Ответ:____________

Задача для самостоятельного решения

Задача №2. Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?

Первый способ:

Наименование веществ, растворов, смесей, сплавов

% содержание вещества (доля содержания вещества)

Масса раствора (смеси, сплава)

Масса вещества

Второй способ:

х г

+

=

Ответ:___________________

Третий способ:

Ответ:_______________