разработка по алгебре на тему 'Решение неравенств с одной переменной' (8 класс)

МКОУ «Плодосовхозская средняя общеобразовательная школа» Кореневского района Курской области

Открытый урок по алгебре

в 8 классе по теме:

Провела: Дугина И.Н.,

учитель математики

МКОУ «Плодосовхозская средняя

общеобразовательная школа»

• Цели урока: Продолжить формирование умений решать неравенства.

Образовательные: совершенствовать навыки решения линейных неравенств с одной переменной с помощью стандартных упражнений, осуществить контроль умений и навыков с использованием КИМ ГИА.

Воспитательные: создать условия для реальной самооценки учащихся; совершенствовать навыки общения.

Развивающие: продолжить развитие умения анализировать, сопоставлять и выделять главное.

Здоровье сберегающие: создать у детей положительную эмоциональную настроенность, использовать здоровье сберегающие действия (смена видов деятельности, физкультминутки) для сохранения работоспособности и расширения функциональных возможностей организма учащихся.

Тип урока : комбинированный

Оборудование: индивидуальные карточки; оценочные листы; мультимедийное оборудование.

Ход урока:

1. Подготовка и мотивация.

Дорогие ребята! Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Очень хочу, чтобы те, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением, что математика - интересный и нужный предмет.

Прежде чем начать сегодняшний урок, я хотела рассказать вам притчу.

НАСТРОЙ НА УРОК : (ЗВУЧИТ МУЗЫКА) 2 МИНУТЫ (слайд 1)

Психологический настрой «Все в твоих руках».

Притча. «Жил мудрец, который знал все. Один человек захотел доказать, что мудрец знает не все. Зажав в ладонях бабочку, он спросил: «Скажи, мудрец, какая бабочка у меня в руках: мертвая или живая?» А сам думает: «Скажет живая - я ее умертвлю, скажет мертвая - выпущу». Мудрец, подумав, ответил: «Все в твоих руках».

Урок проведем под девизом:

«Верь в себя и говори себе, что ты лучший». (слайд2)

Улыбнулись, ребята, друг другу, создали хорошее настроение и начали работу.

У каждого на столах оценочный лист, где указаны основные этапы урока. Запишите там свою фамилию и имя. Я думаю, что вы будете выставлять себе оценки честно и справедливо. В конце урока мы подведём итоги и выставим оценки. И на протяжении всего урока вы помечаете себе мат.термины для составления синквейна.

Фамилия, имя __________________________________________

Устные упражнения

Решение неравенств

Тестирование

Самостоятельная

работа

Оценка

Итого:

Оценка: _______________________________________________________

2.Актуализация опорных знаний.

1. У римского мимического поэта эпохи Цезаря и Августа Публия Сира есть замечательные слова

«Всякий день есть ученик дня вчерашнего». (слайд 3)

● Учащиеся выполняют устные упражнения (слайд 4,5,6)

(спрашивать определения, линейные неравенства, равносильные неравенства)

1При решении неравенств используются следующие свойства:

Если из одной части неравенства перенести в другую слагаемое с противоположным

2знаком, то получится равносильное ему неравенство.

Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;

если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

ОЦЕНКИ В ОЦЕНОЧНЫЙ ЛИСТ

2. Постановка проблемы ( надпись на простой доске )

- Изобразите на координатной прямой множество чисел, удовлетворяющих неравенству, и напишите соответствующий промежуток.

а) х 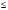5;

б) 4(2 - 5х) - 3(4 + х) > 18 - х; в)4(2 - 5х) - 3(4 + х) = 18 - х

(а, , решает на планшете)

Вы смогли выполнить задание б?

- Почему же это задание не получилось? Чем оно отличается от предыдущих неравенств?

(- Нет.

- Оно не такого вида.

- В нем есть скобки.

- Слагаемые с переменной х в левой и правой частях неравенства.

- Такие неравенства мы решать не умеем).

- Какова же будет тема нашего урока?

- Сколько переменных в неравенстве?

- Уточните тему нашего урока.

- Какую цель вы поставите перед собой на этот урок? Чего вы должны достигнуть?

(- Решение неравенств с одной переменной.

- Мы должны на уроке научиться решать неравенства.)

- Открываем тетради, записываем на полях число и тему урока.

Давай те же решим это неравенство

- Ребята, посмотрите на решение уравнения на доске.

- Теперь посмотрите на неравенство. В чем сходство и отличие уравнения и неравенства?

4(2 - 5х) - 3(4 + х) > 18 - х;

Алгоритм решения неравенств с одной переменной.

1. Раскрыть скобки и привести подобные слагаемые.

2. Сгруппировать слагаемые с переменной в левой части неравенства, а без переменной - в правой части, при переносе меняя знаки.

3. Привести подобные слагаемые.

4. Разделить обе части неравенства на коэффициент при переменной, если он не равен нулю.

5. Изобразить множество решений неравенства на координатной прямой.

6. Записать ответ в виде числового промежутка.

● Как говорил римский баснописец первой половины I в. н. э. Федр: «На примерах учимся»

● применим и мы на примерах использование алгоритма решения неравенств.

Отдельно на листах решения

ОЦЕНИТЬ В ОЦЕНОЧНЫХ ЛИСТАХ

Проведем физминутку

Физкультминутка для глаз.(Слайд ) (1мин)

Рисуй глазами треугольник.

Теперь его переверни

Вершиной вниз.

И вновь глазами

Ты по периметру веди.

Рисуй восьмерку вертикально.

Ты головою не крути,

А лишь глазами осторожно

Ты вдоль по линиям води.

Зажмурься крепко, не ленись.

Глаза открываем мы, наконец.

Зарядка окончилась.

Ты молодец!

● Китайский мудрец Сюнь-цзы сказал «В учении нельзя останавливаться».

Творческое задание - сообщение «Происхождение знака неравенства».

Открывает свою презентацию

(4мин)

Понятия «больше» и «меньше» наряду с понятием равенства возникли в связи со счетом предметов и необходимостью сравнивать различные величины. Понятиями неравенства пользовались уже древние греки. Например, Архимед (III в. до н. э.), занимаясь вычислением длины окружности, указал границы числа π.

Ряд неравенств приводит в своем знаменитом трактате «Начала» Евклид. Он, например, доказывает, что среднее геометрическое двух положительных чисел не больше их среднего арифметического и не меньше их среднего гармонического.

Однако все эти рассуждения проводили словесно, опираясь в большинстве случаев на геометрическую терминологию. Современные знаки неравенств появились лишь в XVII- XVIII вв. Знаки < и > ввел английский математик Томас Гарриот (1560-1621) года жизни. Он был первым алгебраистом XVII века, являлся воспитанником Оксфордовского университета составитель ценного описания и карты исследованной им части Северной Америки, карты Луны, которую он наблюдал через зрительную трубу в одно время с Галилеем.

Новыми полезными знаками Гарриота явились знаки > и < для отношений «больше» и «меньше», он их употребил при рассмотрении вопроса о наличии у кубического уравнения положительных корней. Вывод соответствующих условий, предложенный Гарриотом, заслужил впоследствии высокую оценку Жоржа Лагранжа, но по существу эти условия имелись еще у Виета.

Знаки ≤ и ≥ ввел математик Пьер Бугер (1698-1758)года жизни.

Это французский ученый, один из основателей фотометрии, "Трактат о корабле, о его конструкции и о его движении.

Самое интересное, что Бугер сознавал в целом недостаточную теоретическую подготовленность судостроителей того времени, поэтому его книга написана простым языком и не загромождена сложными математическими выкладками, что сделало ее на долгие годы учебником для кораблестроителей.

● По словам великого немецкого поэта и мыслителя Гёте «Недостаточно только получить знания; надо найти им приложение. Недостаточно только желать; надо делать».

● Последуем эти словам и начнём учиться применять полученные сегодня знания при выполнении упражнений.

● При выполнении упражнений вы можете пользоваться справочным материалом, который есть на каждом столе.

Работа по закреплению материала ( работа в парах ).

У каждого на столе находятся карточка для парной работы. Сначала один ученик решает и комментирует решение первого неравенства соседу, затем наоборот. Второе неравенство решает каждый самостоятельно. После окончания работы оцените ее , затем оцените работу соседа, обменявшись тетрадями. Свои оценки проставьте в оценочный лист.

Проверка под камеру (когда самостоятельно)

● По мнению Н. К. Крупской «… Математика - это цепь понятий: выпадет одно звёнышко - и не понятно будет дальнейшее».

● Проверим, насколько крепка цепь наших знаний.

• Тестирование на компьютерах

• оценки проставьте в оценочный лист.

Подведение итогов урока. Рефлексия.

● Что нового мы узнали на уроке?

И прежде чем закончить урок, мне бы хотелось, чтобы

ребята сами оценили свою работу на уроке.

0

-50 

-100 

+50 

+100 

«закипел»

«равнодушен»

«примерз»

- Отметьте на числовой прямой промежуток как ты провел урок?

СОСТАВИТЬ СИНКВЕЙН В ПАРАХ

Неравенство.

Алгебраическое, логарифмическое.

Сравнивать, решать, находить.

Утверждение о разности двух величин.

Математика.

Неравенство

Будет решаться

Быстро, красиво и легко

Если знаешь методы их решения

Хорошо

• Домашнее задание

* Карточка из ГИА

*Синквейн «Урок»

● «Как приятно, что ты что - то узнал», - сказал когда - то французский комедиограф Мольер.

Всем спасибо за урок! Желаю успехов!