Урок по математики для 7 класс с презентацией по теме: «Линейная функция и ее график»

Линейная функция и её график

Тип урока: изучение нового материала

Цель урока: выяснить зависимость положения графиков линейной функции от значений k и b

Образовательные:

• развивать умение обобщать и систематизировать изученный материал;

• научить определять по значениям k и b положение графиков на координатной плоскости;

• по формуле линейной функции научить определять соответствующий ей график.

Развивающие:

• развивать способности применять теоретические знания на практике;

• развивать логическое мышление, умение применять свои знания при изучении линейной функции;

• развивать аналитические способности детей.

• прививать культуру математической речи.

Воспитательные:

• воспитывать интерес к изучению математики;

• воспитывать эстетику в выполнении чертежей.

План урока

1. организационный момент

2.Актуализация знаний

3. Изучение нового материала

4. Практическая работа

5. Итог урока

6. д/з

Этап урока

Деятельность учителя

Деятельность учащихся

1.Организационный момент

Сообщить учащимся тему и цели урока.

Учащиеся записывают тему в тетрадь

2.Актуализация ранее полученных знаний

1. Какой вид имеет формула, задающая линейную функцию?

2. Из данных функций выделите линейные:

1. у=-2,4х-4; 2. у=; 3. у=3х-4; 4. у=0,2х-4

5. у=-х²-1; 6. у=3х+2,5; 7. у=2,4х; 8. у=5х²;

9. у=3; 10. у=-4х; 11. у=-х³; 12. у=-10; 13. у=+1

3) Что представляет график линейной функции?

Сколько точек необходимо для построения

- Разбейте функции, заданные формулами на группы:

у = 2х - 3

у = 6

у = 7 х

у =

у = - х

у = - 12

у = 0

у = х

- Назовите числа k и b в формулах линейных функций.

1)

2) 1, 3, 4, 6, 7, 9, 10, 12

3) графиком линейной функции является прямая линия.

Для построения линейной функции достаточно двух точек.

группа: у = 2х - 3

группа: у = 7 х; у = ; у = - х; у = х.

группа: у = 6; у = - 12; у = 0.

у = 2х - 3 k=2, b=-3;

у = 6 k=0, b=6;

у = 7 х k=7, b=0;

у = k=1/2, b=0;

у = - х k=-1, b=0;

у = - 12 k=0, b=-12;

у = 0 k=0, b=0;

у = х k=1, b=0

3.Изучение нового материала

- Внимательно посмотрите на ранее приведённые примеры, меняются ли значения k и b в этих функциях

- Какие могут принимать значения k и b в функции y = kx+b

(Анализируя разбиение функций на группы в зависимости от значений k и b, рассматриваем частные случаи линейной функции и составляем удобную и наглядную таблицу)

- Но рассмотрение частных случаев линейной функции без построения соответствующих им графиков, будет не полным. Рассмотрим построение некоторых функций.

1. График функции у = k х, k 0 При b = 0 линейная функция у = k х + b имеет вид у = k х. Её график - прямая, проходящая через начало координат. Для построения этой прямой, достаточно задать какую-нибудь одну её точку, отличную от начала координат.

- Если k = 1, то функция имеет вид у = х, постройте её график.

(Учащиеся выполняют построение рассмотренной функции в тетради)

- Чем является график данной функции для координатной плоскости?

- Если k = - 1, то функция имеет вид у = - х, постройте её график.

(Учащиеся выполняют построение рассмотренной функции в тетради)

- Чем является график данной функции для координатной плоскости?

2. График функции у = b.

При k = 0 линейная функция у = k х + b имеет вид у = b.

(Учащиеся выполняют построение рассмотренной функции в тетради)

- Как расположен график данной функции?

Если не только k = 0, но и b = 0, то функция у = k х имеет вид у = 0.

(Учащиеся выполняют построение рассмотренной функции в тетради)

- Как расположен график данной функции?

Меняются

(k=0, b=0; k>0, b=0; k<0, b=0; k>0, b<0; k>0, b>0; k<0, b<0; k<0, b>0; k=0, b>0; k=0, b<0

k ^{= 0,}

^{b = 0}

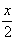
k ^{= 0,}

^{b > 0}

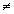
k ^{= 0,}

^{b < 0}

k ^{> 0,}

^{b < 0}

k ^{> 0,}

^{b > 0}

k ^{> 0,}

^{b = 0}

k ^{< 0,}

^{b < 0}

k ^{< 0,}

^{b > 0}

k ^{< 0,}

^{b = 0}

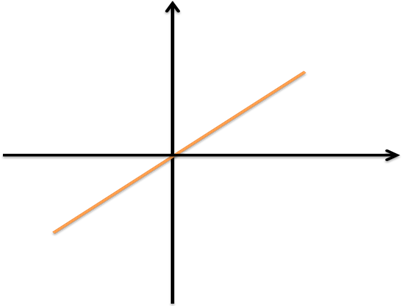
k = 1 ; y = x

Прямая, являющаяся

биссектрисой I и III

координатных углов

k = - 1 ; y = - x

Прямая, являющаяся

биссектрисой II и IV

координатных углов

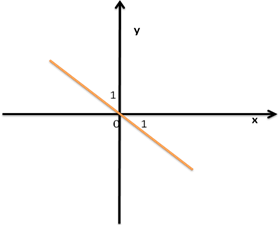
Прямая, параллельная оси Ох и

пересекающая ось Оу в точке с ординатой b.

k = 0 ; у = 0

График совпадает с осью Ох

4.Практическая работа

Задание №1.

- Постройте график функции у = k х и определите в каких четвертях проходит данная функция.

№ 1: y = -2x;
№ 2: y = 2x;
№ 3: y = 1/4x.

Задание №2.

- Постройте график функции вида y = b:

№ 1: y = -3;
№ 2: y = -1;
№ 3: y = 4;

Задание №3. (учебник "Алгебра 7 класс" Ш. А. Алимов и др.)

а) Выполнить № 580 у доски

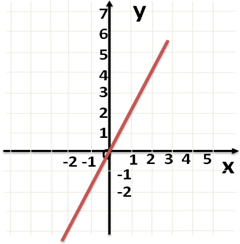
(Ответ: y(0) = -1; y(1) = 2; y(2) = 5)

(Ответ: x = -1; x = 2; x = 1/3)

5. итог урока

- Сделать выводы о влиянии значений параметров k и b на положение графиков.

При k = 0 линейная функция имеет вид у = b. Её графиком является прямая, параллельная оси 0х и пересекающая ось 0у в точке с ординатой b; Если k = 1, то функция имеет вид у = х, её график - прямая, являющаяся биссектрисой I и III координатных углов; Если k = - 1, то функция имеет вид у = - х, её график - прямая, являющаяся биссектрисой II и IV координатных углов; Если не только k = 0, но и b = 0, то функция у = k х имеет вид у = 0. В этом случае её график совпадает с осью Ох.

6. Д/З

учебник "Алгебра 7 класс" Ш. А. Алимов и др.

№ 581 (2, 4, 6), № 584..