- Учителю
- разработка урока по математике на тему: 'Линейная функция и ее график' (6 класс)
разработка урока по математике на тему: 'Линейная функция и ее график' (6 класс)
Цели урока:
образовательные: обобщить и систематизировать материал по теме: «Линейная функция, ее свойства и график»;
развивающие: развитие потребности к самообразованию, интереса к изучаемому предмету; работа по развитию умения обобщать полученные результаты;
воспитательные: формировать интерес к данному предмету, содействовать воспитанию интереса к математике, особенно в условиях информатизации общества, активности, умению общаться, аргументировано отстаивать свои взгляды.
Задачи урока: применение знаний, контроль знаний по теме.
Тип урока: обобщение и систематизация знаний.
Необходимое оборудование к уроку: мультимедийное оборудование, интерактивная доска, раздаточный материал.
Ход урока
I. Организационный момент.
Приветствие учащихся, положительный настрой на урок.
Разгадав слова по горизонтали, вы узнаете ключевое слово урока.
1.Точный набор инструкций, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное время.
2.Одна из координат точки.
3Зависимость одной переменной от другой, при которой каждому значению аргумента соответствует единственное значение зависимой переменной.
4Французский математик, который ввел прямоугольную систему координат.
5.Угол, градусная мера которого больше 900, но меньше 1800 .
6.Независимая переменная.
7.Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции.
8.Дорога, которую мы выбираем.
А
Л
Г
О
Р
И
Т
М
А
Б
С
Ц
И
С
С
А
Ф
У
Н
К
Ц
И
Я
Д
Е
К
А
Р
Т
Т
У
П
О
Й
А
Р
Г
У
М
Е
Н
Т
Г
Р
А
Ф
И
К
П
Р
Я
М
А
Я
II. Постановка цели урока. Сл. 4.
III. Обобщение и систематизация пройденного материала.
Фронтальный опрос учащихся по слайдам презентации.
Повторим основные понятия темы: на интерактивной доске появляются вопросы по теме, на которые учащиеся отвечают устно.
-
Экспресс - опрос. Сл.5.
Какую функцию называют линейной?
Что является графиком линейной функции?
Какую функцию называют прямой пропорциональностью?
Что является графиком прямой пропорциональности?
В каком случае графики двух линейных функций являются параллельными прямыми?
В каком случае графики двух линейных функций пересекаются?
Какой из этих графиков является графиком линейной функции? Сл.6.
Какой из этих графиков является графиком прямой пропорциональности? Сл.7.
-
Задания для устной работы. Сл.8.
За минуту составьте самое длинное слово, связанное с темой нашего урока, из букв, которые даны на карточках:
К, Ф, А, Д, И, О, Г, Р. Слово - ГРАФИК.
-
«Найди ошибку». Сл.15,16,17.
Ученик допустил ошибку при построении графика одной из функций.
На каком рисунке ошибка?
* « Выполни устно»
1. График функции y = -2x проходит через точку,
абсцисса которой -3. Какова ордината этой точки?
Ответ: y = 6
2. В каких координатных четвертях проходит график
функции:
а) y = 4x; б) y = -5x ?
Ответ: a) I и III; б) II и IV.
-
«Кто быстрее»
А) Определи, сколько точек пересечения имеют графики функции, не выполняя построения.
1.у=2х+5 у=2х+3
2.у=4-3х у = -3х+1
3.у=8х-2 у=4х-2
4.у=5х у=5х+2
5.у=0,1х+8 у=3х
Ответы
0
0
1
0
1
Б) Подставьте вместо знаков * такие числа, чтобы графики линейных функций были параллельны:
у = 8х + 12 и у = *х - 3
у = - 5х - 3 и у = *х + 1
В) Подставьте вместо знаков * такие числа, чтобы графики линейных функций пересекались:
у = 7х + 8 и у = *х - 4;
у = 2х + * и у = *х - 8.
-
Интересные факты применения линейной функции.
А) Шкала Цельсия и Фаренгейта
Вы когда-нибудь слышали про шкалу Фаренгейта? Это что-то вроде шкалы Цельсия, только по шкале Цельсия измеряют температуру у нас в стране, а по шкале Фаренгейта - в Америке и Англии. Две эти шкалы тесно связаны между собой. Если температура по шкале Цельсия обозначить за x, а температуру по шкале Фаренгейта за y,то эту зависимость можно записать так у = 1,8х+ 32 . Значит, когда у нас, например, нуль
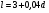 градусов, то по шкале Фаренгейта это 32 градуса. А температура 10 градусов по Цельсия соответствует 50 градусов по Фаренгейту.
градусов, то по шкале Фаренгейта это 32 градуса. А температура 10 градусов по Цельсия соответствует 50 градусов по Фаренгейту.
Б) Длина растущих волос вычисляется по формуле
Например, первоначальная длина 3 см + 0,4 мм в сутки.
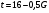 В) Сон ребенка.
В) Сон ребенка.
G - возраст ребенка
-
«Кто быстрее решит»
А) Найдите значение y, соответствующее x = - 12, если линейная функция задана формулой y = 0, 5x + 3.
Выбери правильный ответ
Б) Линейная функция задана формулой y = -2x + 8
Найдите значение x, при котором y = 18.
Решение:
y=-2x+8, y=18
-2x+8=18
-2x=18-8
-2x=10
x=10:(-2)
x=-5
В) Назовите координаты точек пересечения графика данной функции с осями координат. Сл.33,34,35,36.
Г) Найти координаты точки пересечения графиков функций
у = 1 - 2х и у = х - 5 и построить графики этих функций.
IV. Подведение итогов урока. Выставление оценок. Сдача работ.
Учащиеся читают стихотворение, вставляя пропущенные слова.
Среди многих функций
Есть одна нужнейшая
Важная, старейшая.
Зовем ее
линейная.
Графиком которой
Является
прямая,
Строгая, красивая,
Бесконечная такая.
Если k1 равно k2,
Прямые
параллельные
тогда.
При k1, не равном k2,
Прямые
пересекаются
всегда,
И каков же тут итог,
Если наш учитель строг?
Любой ответ по «месту
жительства» прямых
Найдем мы при условиях
любых.
V. Домашнее задание.
Найти и записать примеры линейной функции в жизни.