'График гармонических колебаний' (конспект урока, 10 класс, А. Г. Мордкович)

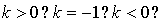
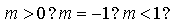
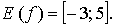
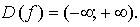
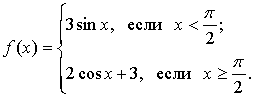
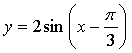
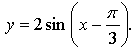
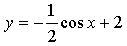
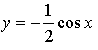
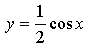
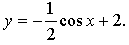
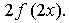
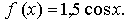
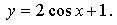
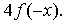
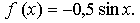
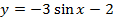
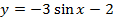
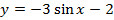
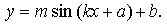
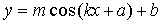
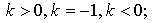Преобразование графиков тригонометрических функций.

График гармонических колебаний.

Цели: 1) закрепить умение строить график функции вида y = m · f(x), где для функций у = sin х, у = cos х.

2) закрепить умение строить график функции у = f(kx), где для функций у = sin х, у = cos х; сформировать умение строить графики функций вида и

3) изучение нового материала, построение графика гармонического колебания маятника

Ход урока

1. Организационный момент. Здравствуйте. На прошлом уроке мы научились строить графики функций y = m · f(x), и у = f (k ∙ x). Сегодня мы продолжим тему преобразование графиков тригонометрических функций и рассмотрим функции вида y=m∙f(kx+a)+b.

II. Устная работа.

Вспомним:

- алгоритм построения графика функции y = m · f(x), где m  0: (слайд 2)

1) Построить график функции у = f(x);

2) Осуществить его растяжение от (сжатие к) оси 0х с коэффициентом т;

3) Растянутый график подвергнуть преобразованию симметрии относительно

оси х.

- алгоритм построения графика функции у= f(k∙x), где k < 0: (слайд 3)

1) Построить график функции у = f(x).

2) Осуществить его растяжение от (сжатие к) оси у с коэффициентом k.

3) Растянутый график подвергнуть преобразованию симметрии относительно

оси у, если функция нечетная; и оставить без изменения, если функция четная.

Выполним упражнение (Слайд 4):

1. Объясните, каким образом можно получить из графиков функций

у = sin х или у = cos х графики следующих функций:

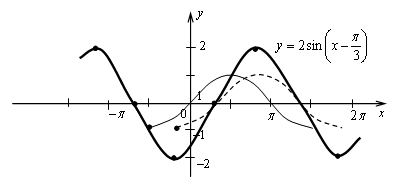
1. у = -3sinx; 2) y = cos (-2x); 3) y = 2 sin (x-π/2)

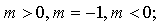
(Слайд 5) (Слайд 6)

(Слайд 7)

III. Проверочная работа. (Слайд 8)

Вариант 1

1. Постройте график функции .

2. Известно, что Найдите :

Вариант 2

1. Постройте график функции

2. Известно, что Найдите:

IV. Объяснение нового материала.

В повседневной жизни мы часто сталкиваемся с повторяющимися движениями. Например, часы с маятником, которые колеблются из стороны в сторону. В физике такой маятник называется математическим. Детская игрушка ё-ё яркий пример пружинного маятника. В физике вы уже познакомились с таким термином как колебания. Напомню, любые периодически повторяющиеся движения называются колебаниями.

Ученые заинтересовались: существует ли зависимость местоположения маятника от времени, т.е. можно ли сказать где будет находиться маятник в конкретный момент времени, если знать его положение в начальный момент времени. Для этого был проведен опыт:

Математический маятник подвесили над равномерно движущейся бумажной лентой. Из маятника высыпался песок, который оставлял след на бумажной ленте. В результате эксперимента было обнаружено, что след совпадает с синусоидой, т.е. функцию зависимости положения от времени можно записать как

(Слайд 10)

Рассмотрим пример: Пружинный маятник колеблется по закону x(t)=3sin(2x+π/2). Построить график гармонического колебания маятника.

(слайд 11)

Важное замечание: Мы знакомы с преобразованиями у=f(kx)+b и y=f(x+b). Как ведут себя графики функций при этих преобразованиях мы знаем. Но мы не знаем преобразование y=f(kx+b), и как изменится график функции при этом преобразовании мы тоже не знаем. Поэтому, мы не можем построить график гармонического колебания в таком виде. Вынесем за скобки 2 и получим x(t)=3sin(2(x+π/6)). Построим график функции. При построении графика гармонического колебания маятника мы использовали преобразования графика:

Y=f(x+b), где b=π/6; y= f(kx), где k=2; y= mf(x), где m=3.

Упражнение 2: (у доски 1 ученик)

Слайд (14) 1ученик у доски.(слайд16)

Дополнительно:

№ 13.7 (а; б), № 13.8 (а; б), №13.9 (а), № 13.10 (а).

Решение:

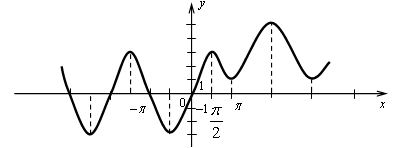
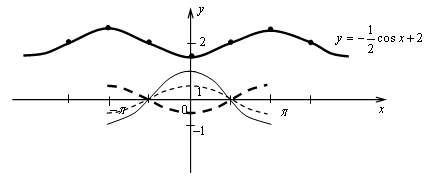
№ 13.7 (б).

Порядок построения:

1) Ветвь графика у = cos х.

2) Ветвь графика сжатием исходного графика в 2 раза к оси 0х.

3) Ветвь графика отображением предыдущего графика относительно оси 0х.

4) Ветвь графика параллельным переносом предыдущего графика на 2 единицы вверх.

5) Достраиваем весь график.

№ 13.8 (а).

Порядок построения:

1) Ветвь графика у = sin х;

2) Ветвь графика параллельным переносом исходного графика на единицы вправо.

3) Ветвь графика растяжением предыдущего графика в 2 раза от оси 0х.

4) Достраиваем весь график.

№ 13.9 (а).

№ 13.10 (а).

1)

2) Общего вида.

3) Ограничена.

4) у_наим = -3; у_наиб = 5;

5) Непрерывна.

6)

V. Итоги урока.

Вопросы учащимся:

- Каким способом, зная график функции у = f(x), построить график функции y = m · f(x), где

- Каким способом, зная график функции у = f(x), построить график функции у = f(kx), где

Домашнее задание: № 13.8 (в; г), № 13.9 (б), № 13.10 (б), 13.16