Методическая разработка урока по математике Показательные неравенства СПО

ГОСУДАРСТВЕННОЕ ОБЛАСТНОЕ БЮДЖЕТНОЕ

ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ»

.

Методическая разработка урока

по общеобразовательной дисциплине

«Алгебра и начала математического анализа; геометрия»

на тему

Показательные неравенства

Разработала: преподаватель математики

Клещина Наталья Вячеславовна

Липецк 2016

Пояснительная записка

Показательная функция, как сказал Пьер Кури не перестает нас удивлять! Ее применение велико, только за последние годы из Нобелевских лауреатов, получивших премию за исследования в области математики, биологии, физики с использованием показательной функции 6 ученых.

В структуре изучаемой дисциплины «Алгебра и начала математического анализа; геометрия» выделяется следующий раздел: «Корни, степени и логарифмы». Содержание раздела «Корни, степени и логарифмы» включает тему урока «Показательные неравенства» .

В результате изучения данной темы студент должен

Знать:

-определение показательной функции и ее свойств;

-виды графиков показательной функции с разным показателем;

-определение показательного неравенства;

Уметь:

-решать показательные неравенства;

-применять методы решения показательных неравенств при решении задач;

-определять основные свойства показательной функции, иллюстрировать их на графиках;

-строить графическое решение показательного неравенства;

-решать прикладные задачи с применением показательных неравенств;

Тема урока : Показательные неравенства

Образовательная цель: способствовать формированию у студентов предметных компетенций:

- формирование познавательных УУД ;

-научить решать показательные неравенства различными методами;

-использовать свойства показательной функции при графическом решения

неравенств;

Развивающая цель: способствовать развитию у студентов метапредметных компетенций:

-коммуникативных - формирование мыслительной, речевой деятельности, пространственного воображения, навыка сотрудничества;

-регулятивных - умение управлять собственной деятельностью.

Воспитательная цель: способствовать формированию у студентов личностных компетенций:

-смыслообразование - умение субъектного целеполагания;

-самоопределение - самооценка.

Тип урока: комбинированный урок

Вид урока: лекция + практическая работа

Методические приемы:

-самостоятельная работа (тест);

-практический- решение математических и прикладных задач.

Оборудование и наглядные средства обучения: компьютерный класс с ОС Windows 8 и пакетом программ Microsoft Office 2010 (10 ПК), мультимедийный проектор, интерактивная доска SmartBoard, программа Notebook, колонки, демонстрационный и раздаточный материал, презентация в Notebook, в Power Point.

Методическая цель: способы активизации мыслительной деятельности студентов

Ход урока:

I.Организационный момент: Подготовка учащихся к уроку

(проверка отсутствующих на уроке, наличие тетрадей)

II. Сообщение темы и целей урока.

На уроке будут рассмотрены новые для обучающихся неравенства - показательные, решение которых требует хорошего знания теоретического материала. Данные неравенства ежегодно присутствуют в вариантах ЕГЭ по математике.

Актуализация знаний.

Теоретический опрос:

а) определение показательной функции;

(Функция вида называется показательной функцией.)

б) какова область определения показательной функции;

в) какова область значений показательной функции;

г) в каком случае показательная функция является возрастающей, убывающей;

y = a^x , a > 1 возрастает, y = a^x , 0< a < 1 убывает

д) как расположен график;

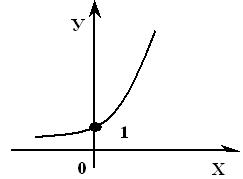y = a^x , a > 1 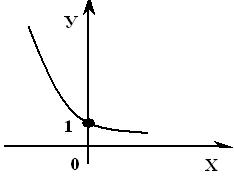y = a^x , 0< a < 1

е) каковы основные методы решения показательных уравнений (метод замены, однородное уравнение, разложение левой части уравнения на множители и переход к совокупности, функционально-графический, метод интервалов);

III. Изучение нового материала

Теоретическая часть.

1. Введение знаний.

1) Простейшие показательные неравенства имеют вид

решений не имеет, а неравенство выполняется при всех значениях аргумента, поскольку (Рассказ сопровождается графической иллюстрацией)

При выполняется равенство . Если , то в силу возрастания показательной функции неравенство выполняется при, а неравенство выполняется при . (Рассказ сопровождается графической иллюстрацией)

Если , то в силу убывания показательной функции неравенство выполняется при а неравенство выполняется при . . (Рассказ сопровождается графической иллюстрацией)

Рассмотреть примеры:

Используя свойство монотонности показательной функции делаем вывод, что неравенство при равносильно неравенству а при равносильно неравенству

Конспект .

2) Рассмотрим методы решения показательных неравенств, не являющихся простейшими. При их решении используются приёмы преобразования выражений, стоящих в левой и правой частях неравенства, аналогичные тем, которые использовались и при решении показательных уравнений.

а) Метод замены переменной. В этом случае новая неизвестная подбирается так, чтобы относительно неё неравенство не было показательным.

Пример 1: Сведение к квадратному неравенству.

.

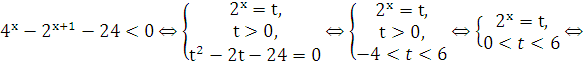
Ответ:

Пример 2: Сведение к рациональному неравенству, которое решаем применяя метод интервалов для непрерывных функций.

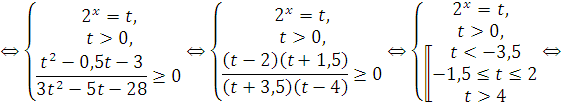
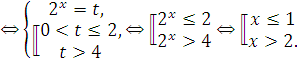
Ответ:

б) Решение однородных неравенств. При решении однородных неравенств используется свойство показательной функции , производим деление обеих частей неравенства на положительную величину и вводим новую переменную. Однородное неравенство первой степени +n решается делением обеих частей неравенства на , а однородное неравенство второй степени решается делением на

Пример 3:

Решение:

Так как для любых x, то разделив обе части неравенства на , получим неравенство, равносильное данному:

-

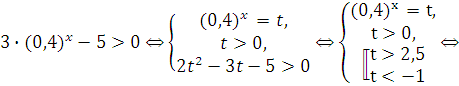
Ответ: (-

в) Метод интервалов.

Пример 4:

Решение.

Рассмотрим функцию f(x), областью определения которой является множество неотрицательных чисел. Находим нули функции, решив уравнение . Делим обе части уравнения на , после преобразований получим уравнение

откуда Последнее уравнение не имеет решения, а уравнение имеет единственный корень, равный 4. Нуль функции разбивает область определения на промежутки и, в которых функция (в силу своей непрерывности) сохраняет знак.

f(1)

f(9)

Итак, исходное неравенство выполняется при

Ответ:

г) Функционально-графический метод.

Пример:

Решение. Функции иопределены на всём множестве действительных чисел. Функция возрастающая на R, а функция убывающая на R, значит, уравнение имеет не более одного корня. Не сложно убедиться в том, что 1 является единственным корнем уравнения. Таким образом, графики функций имеют одну точку пересечения. Неравенство имеет решение тогда, когда график функции лежит не выше графика функции то есть при

Ответ: (

Практическая часть.

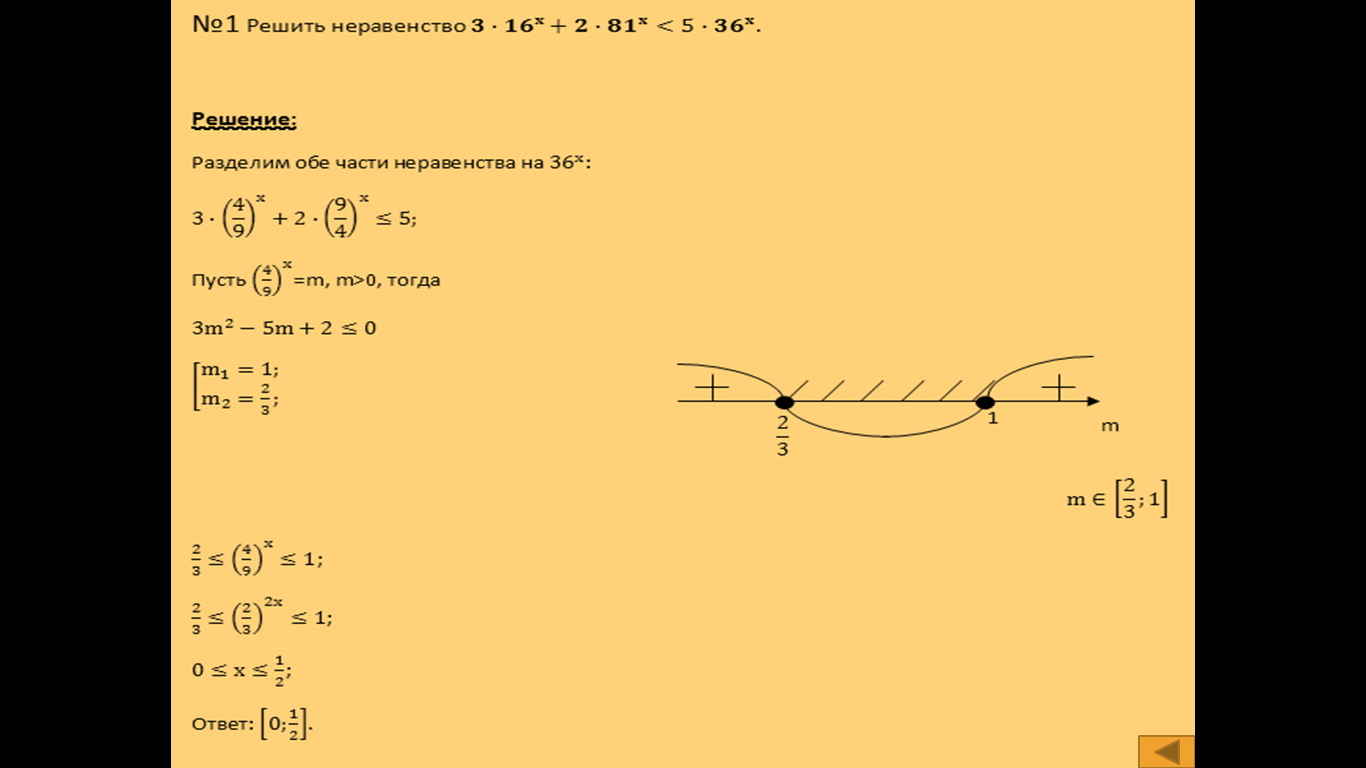
Из предложенных неравенств выбрать наиболее рациональный способ для их решения:

а)

Ответ: однородное неравенство, делим обе части, например, на и введение новой переменной .

б)

Ответ: с помощью замены сводим к решению дробно-рационального неравенства.

в)

Ответ: решается функционально-графическим способом.

г)

Ответ: использование свойства монотонности показательной функции. Приложение 1

IV. Закрепление пройденного материала: Приложение 2

V. Итоги урока: Проверка теста, выставление оценок

Домашняя работа Расписать подробное решение неравенств из теста.

Интернет-ресурсы:

www.ziimag.narod.ru - персональный сайт автора Мордковича А. Г. "Практика развивающего обучения".

www.math.ru -Интернет - поддержка учителей математики.

www.it-n.ru-Сеть творческих учителей. Материалы и ресурсы, касающиеся использования ИКТ в учебном процессе:

- библиотека готовых учебных проектов с применением ИКТ, а также различные проектные идеи, на основе которых можно разработать свой собственный проект;

- библиотека методик проведения уроков использованием разнообразных электронных

ресурсов;

- руководства и полезные советы по использованию программного обеспечения в учебном процессе;

- подборка ссылок на интересные аналитические и тематические статьи для педагогов.

www.exponenta.ru -Образовательный математический сайт. Содержит материалы по работе с математическими пакетами Mathcad, MATLAB, Mathematica, Maple и др. Методические разработки, примеры решения задач, выполненные с использованием математических пакетов. Форум и консультации для студентов и школьников.

http:school-collection.edu -Единая коллекция цифровых образовательных ресурсов. Цифровые образовательные ресурсы (ЦОР) к учебникам.

www.intellectcentre.ru</ - сайт издательства «Интеллект-Центр», -тренировочные материалы, демонстрационные версии, банк тренировочных заданий с ответами, методические рекомендации и образцы решений.

Приложение 1.

Методы решения произвольных показательных неравенств .

Решение большинства показательных неравенств сводится к решению простейших показательных неравенств.

А. Метод уравнивания оснований.

Примеры.

Пример 1. Решите неравенство:

Решение.

О.О.: х

Так как 0,0625=, тогда данное неравенство можно записать в виде:.

Показательная функция y= ( 0 является убывающей на R, значит меньшему значению функции соответствует большее значение аргумента, то есть

, но 4= , тогда , но показательная функция y= (21) является возрастающей на R, поэтому большему значению функции соответствует большее значение аргумента. В результате этих рассуждений получим и решим следующее неравенство: .

..

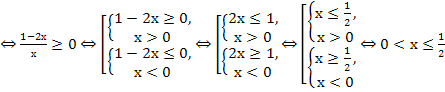Ответ: .

Пример 2. Решите неравенство: .

Решение.

О.О.: х

Ответ: .

В. Метод решения, основанный на разложении на множители.

Примеры.

Пример 1. Решите неравенство: х

Решение.

О.О.: хR

хх.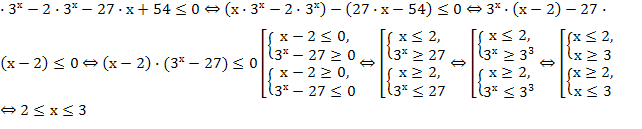

Ответ: .

Пример 2. Решите неравенство: 3 .

Решение.

3 3+(+

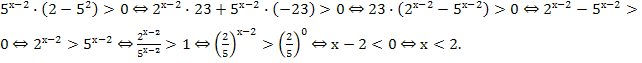
Ответ: .

С. Метод введения вспомогательной переменной.

С помощью подстановки , где t, неравенство приводится либо к квадратному неравенству относительно переменной t, либо к какому-нибудь другому неравенству относительно переменной t, решается относительно t , а затем ищется значение переменной х.

Примеры.

Пример 1. Решите неравенство: .

Решение.

О.О.:

Пусть , .

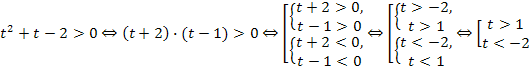Вернемся к переменной х и получим два неравенства:

1) .

решений нет, так как для .

Ответ: .

Пример 2. Решите неравенство: 4 .

Решение.

4 + 3

. Пусть , тогда 4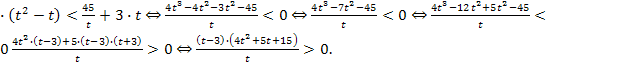

Выделим из многочлена квадрат двучлена:

=, то есть при любом значении t Таким образом, дробь

если t, но t=, тогда .

Ответ: .

D. Неравенства, левая часть которых имеет вид АB,

Неравенства такого типа решаются с помощью деления обеих частей на

.

Примеры.

Пример 1. Решите неравенство: 3.

Решение.

3.

Разделим обе части последнего неравенства на :

3 Введем новую переменную t = , t

3. Вернемся к переменной х:

.

Ответ: .

Пример 2. Решите неравенство: 9.

Решение.

9 .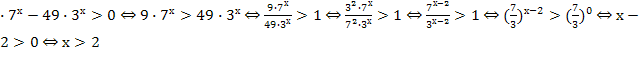

Ответ: .

Е. Графический способ решения.

При решении неравенств графическим способом необходимо рассмотреть две функции, построить их графики в одной системе координат и выяснить при каких значениях аргумента значения одной функции больше (меньше) значений другой функции. Найденные значения аргумента и есть решения неравенства.

Примеры.

Пример 1. Решите неравенство:

Решение.

Чтобы решить данное неравенство графическим способом, рассмотрим две функции: f(x)= и g(x)= 11-х, D(f)=R, D(g)=R.

1.Функция f(x)= - показательная функция по основанию «3». Для построения графика зададим таблицу ее значений:

2. Функция g(x)= 11-х - линейная функция, ее графиком является прямая.

3. Построим графики этих функций в одной системе координат и выясним , при каких значениях переменной х выполнено неравенство: f(x) g(x).

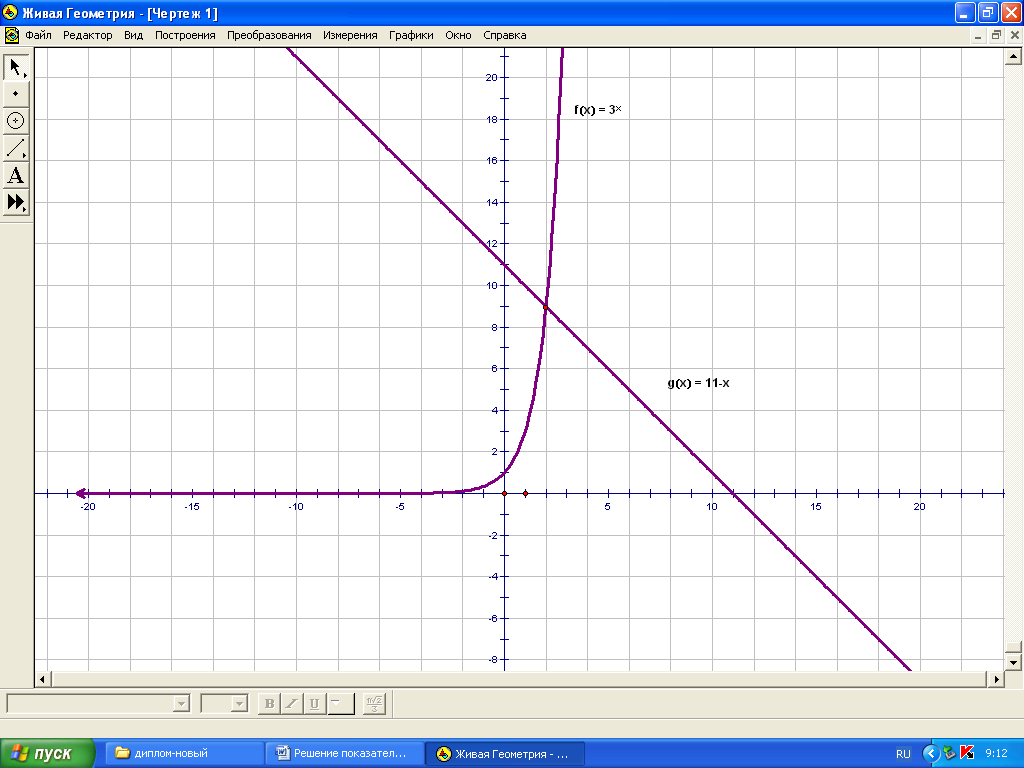
Рассмотрим два интервала: :

если х, то f(x) , f(x) Значит, решением неравенства являются значения х, принадлежащие промежутку .

Ответ: .

Пример 2. Решите неравенство: .

Решение.

Чтобы решить данное неравенство графическим способом, рассмотрим две функции: f(x) = и g(x) = , D(f)=R, D(g)=

1.Функция f(x) = - показательная функция с основанием . Для построения графика зададим таблицу ее значений:

2. Функция g(x)= - функция обратная пропорциональность, ее графиком является гипербола , расположенная во 2-й и 4-й координатных четвертях.

3. Построим графики этих функций в одной системе координат и выясним , при каких значениях переменной х выполнено неравенство: f(x) g(x).

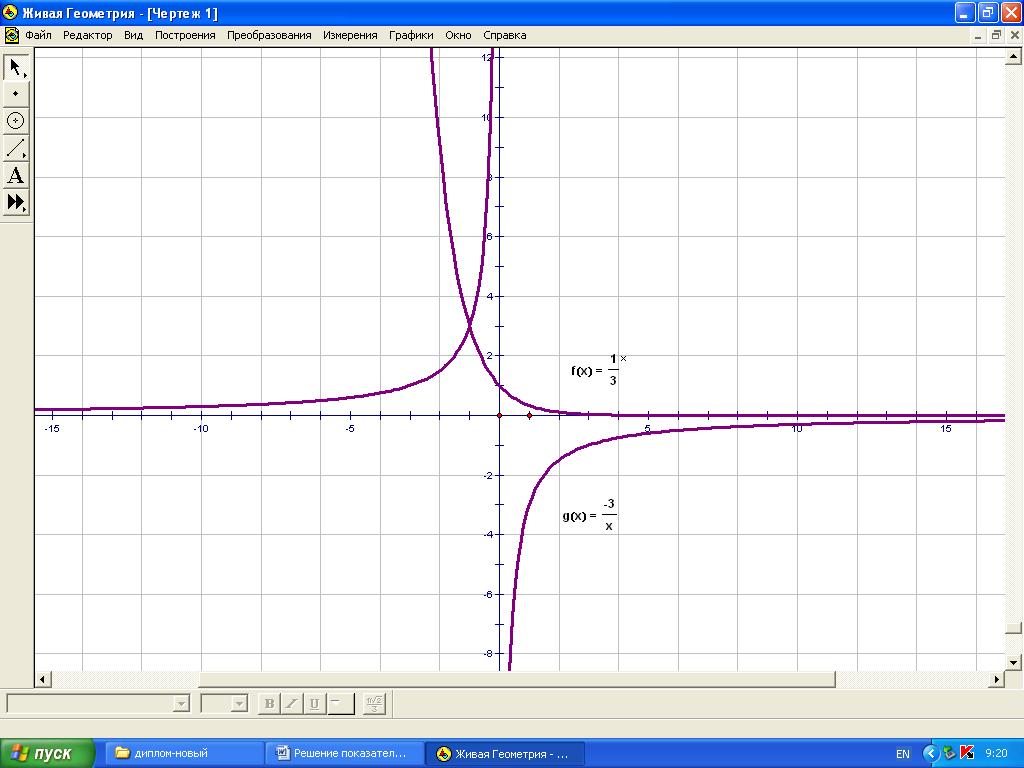
Рассмотрим три интервала: и :

если х, то f(x) , то f(x) Значит, решением неравенства являются значения х, принадлежащие промежутку

Ответ:

Приложения 2.

Тест 1. Показательные неравенства.

Тест 1. Показательные неравенства.

Вариант 1.

Вариант 2.

1.Найти наибольшее целое решение неравенства

1. Найти наименьшее целое решение неравенства