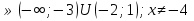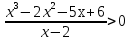- Учителю
- Разработка системы уроков повторения по алгебре для 10-11 классов по теме: «Решение неравенств алгебраическим методом»
Разработка системы уроков повторения по алгебре для 10-11 классов по теме: «Решение неравенств алгебраическим методом»












 Разработка системы уроков повторения, направленных на подготовку к ЕГЭ
Разработка системы уроков повторения, направленных на подготовку к ЕГЭ
по математике по теме
«Решение неравенств алгебраическим методом».
Содержание.
1. Примерное планирование учебного времени.
2. План-конспект урока по теме «Рациональные и дробные рациональные неравенства».
3. Проверочная работа (в одном варианте).
1. Примерное планирование учебного времени. Всего 15ч.
№
Тема
Всего часов
Содержание
Форма контроля
1
Равносильные неравенства
1
Равносильные преобразования неравенств, тождественные преобразования выражений, входящих в неравенство, посторонние решения, потеря решений.
2
Обобщённый метод интервалов
1
Классический метод интервалов. Обобщённый метод интервалов. Точки чётной и нечётной кратности. Нетрадиционный алгоритм решения неравенств методом интервалов.
3
Рациональные и дробные рациональные неравенства
2
Целые рациональные неравенства. Дробные рациональные неравенства. Алгоритм решения целых рациональных неравенств и дробных рациональных неравенств методом интервалов. Решение рациональных и дробных рациональных неравенств обобщённым методом интервалов.
Тест для проверки теоретических знаний
Контрольный тест.
4
Неравенства, содержащие иррациональные выражения.
2
Решение иррациональных неравенств, основанное на свойствах числовых неравенств. Схема решения неравенств обобщённым методом интервалов. Некоторые нюансы в определении знака и особенности упрощенной записи.
Тест для проверки теоретических знаний.
5
Неравенства, содержащие выражения под знаком модуля.
2
Геометрический смысл модуля. Решение неравенств разбиением ОДЗ на подмножества. Решение неравенств, содержащих модули обобщенным методом интервалов и особенности упрощённой записи.
Проверочная работа.
6
Показательные неравенства
2
Решение показательных неравенств. Метод замены. Показательно-степенные неравенства и логарифмирование обеих частей неравенства. Метод интервалов для решения показательно-степенных неравенств.
Самостоятельная работа
Взаимоконтроль.
7
Логарифмические неравенства
2
Схемы решения логарифмических неравенств и потенцирование обеих частей неравенства. Метод замены и использование метода интервалов для упрощения решений.
Самостоятельная работа.
Самоконтроль.
8
Смешанные неравенства
2
Решение смешанных неравенств обобщённым методом интервалов. Решение сложных комбинированных неравенств. Решение неравенств с параметрами методом интервалов.
Контрольный тест
9
Контрольная работа
1
Контрольная работа
2. План-конспект одного из уроков.
Рациональные и дробные рациональные неравенства
( 2 часа)
Цель. Формирование умения применять алгоритм обобщённого метода интервалов для решения рациональных и дробных рациональных неравенств.
Целым рациональным неравенством называют неравенство вида
f(x) - алгебраический многочлен.
- алгебраический многочлен.
Дробным рациональным неравенством называют неравенство вида 
 - алгебраические многочлены. Очевидно, что множество решений дробно-рационального неравенства не должно содержать корней многочлена
- алгебраические многочлены. Очевидно, что множество решений дробно-рационального неравенства не должно содержать корней многочлена 
Решая целые рациональные неравенства методом интервалов, будем следовать алгоритму:
1) запишем неравенство в виде f(x) и рассмотрим функцию f(x);
и рассмотрим функцию f(x);
2) найдём нули функции, решая уравнение f(x)=0;
3) нанесём нули функции на координатную прямую и определим знаки функции на полученных промежутках, учитывая точки чётной и нечётной кратности ;
4) запишем решение неравенства, учитывая его смысловой знак.
Решая дробные рациональные неравенства методом интервалов, будем следовать алгоритму:
1) запишем неравенство в виде 
 и рассмотрим функцию F(x)=
и рассмотрим функцию F(x)=
2) найдём нули и точки разрыва функции, решая уравнения f(x)=0 и =0;
=0;
3) нанесём нули и точки разрыва функции на координатную прямую и определим знаки функции на полученных промежутках, учитывая точки чётной и нечётной кратности;
4) запишем решение неравенства, учитывая его смысловой знак.
При решении неравенств вида  и
и  корни числителя будем отмечать на координатной прямой «заштрихованными» точками, а корни знаменателя - «пустыми».
корни числителя будем отмечать на координатной прямой «заштрихованными» точками, а корни знаменателя - «пустыми».
Пример 1. Решить неравенство 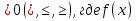
1) Рассмотрим функцию f(x)=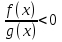 .
.
2) Найдём нули функции, решая уравнение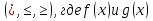
Получим х1,2 = 2, х3,4,5 = - 3, х6 = 7.
3) Корни нечётной кратности: - 3 и 7, а 2 - корень нечётной кратности.
+ - - +
-3 2 7
4) Объединив промежутки, в которых функция отрицательна, запишем ответ
Ответ: (-3;2) U(2;7).
Пример 2. Решить неравенство
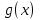
1) Рассмотрим функцию f(x)=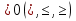
2) Найдём нули функции, решая уравнение 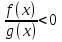 Получим х1,2 = 0, х3 = - 1.
Получим х1,2 = 0, х3 = - 1.
Найдём точки разрыва, решая уравнение 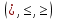 Получим х4 = - 2, х5 = 2.
Получим х4 = - 2, х5 = 2.
3)
- + - - +
-2 -1 0 2 х
4) Так как функция f(x)=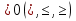 может быть как положительной, так и равной нулю (на это указывает смысловой знак неравенства
может быть как положительной, так и равной нулю (на это указывает смысловой знак неравенства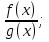 ), то решением неравенства является объединение промежутков, на которых функция неотрицательна и изолированная точка 0.
), то решением неравенства является объединение промежутков, на которых функция неотрицательна и изолированная точка 0.
Ответ: (-2; 1] U (2; +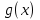 ) U {0}.
) U {0}.
Тест для проверки теоретических знаний по теме «Решение рациональных и дробно-рациональных неравенств».
Укажите все необходимые действия(1,2)
1. Чтобы решить целое рациональное неравенство вида ![]() необходимо:
необходимо:
1) найти нули функции ![]() ;
;
2) найти точки разрыва функции ![]() ;
;
3) нанести нули функции ![]() на координатную прямую и определить знаки функции на полученных промежутках;
на координатную прямую и определить знаки функции на полученных промежутках;
4) нанести точки разрыва функции ![]() на координатную прямую и определить знаки функции на полученных промежутках;
на координатную прямую и определить знаки функции на полученных промежутках;
5) записать промежутки, на которых функция не положительна;
6) записать промежутки, на которых функция отрицательна;
7) записать промежутки, на которых функция положительна.
2. Чтобы решить дробное рациональное неравенство вида ![]() необходимо:
необходимо:
1) найти нули функции ![]() ;
;
2) найти нули функции ![]() ;
;
3) отметить на координатной прямой нули функции ![]() «заштрихованными» кружочками, а нули функции
«заштрихованными» кружочками, а нули функции ![]() - «пустыми»;
- «пустыми»;
4) отметить на координатной прямой нули функции ![]() «пустыми» кружочками, а нули функции
«пустыми» кружочками, а нули функции ![]() - «заштрихованными»;
- «заштрихованными»;
5) отметить на координатной прямой нули функции ![]() и нули функции
и нули функции ![]() «заштрихованными» кружочками;
«заштрихованными» кружочками;
6) записать промежутки, на которых функция ![]() положительна;
положительна;
7) записать промежутки, на которых функция![]() не отрицательна.
не отрицательна.
3 Установите соответствие:
Неравенство
1) х(х-1)(х+2)>0;
3) 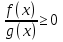 ;
;
2) 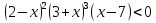 0
0
4) 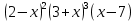
рисунок
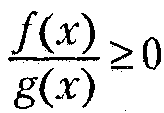
решение (ответ)
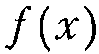
Ответы
Номер задания
1
2
3
Вариант правильного отвена
1; 3; 5.
1; 2; 3; 7.
1 - б - и, 2 - г - к,
3 - а - л, 4 - в - ж.
Самостоятельная работа по карточкам с последующей проверкой по листам самопроверки по теме «Решение рациональных и дробно-рациональных неравенств».
Карточка 1.
№1 Найти целые решения неравенства ![]()
№2 Решить неравенство ![]()
Карточка 2.
№1 Решить неравенство ![]()
№2 Решить неравенство ![]()
Карточка 3.
№1 Решить неравенство ![]()
№2 Решить неравенство ![]()
Карточка 4.
№1 Решить неравенство ![]()
№2 Решить неравенство ![]()
Лист самопроверки к карточке 1.
№1 Найти целые решения неравенства ![]()
Решение:
![]()
![]()
![]()
Рассмотрим функцию: ![]()
Найдём нули: ![]()
![]()
Точки разрыва: ![]()
![]()
![]()
![]()
Так как функция не положительна, то решением данного неравенства является промежуток: ![]() .
.
Запишем целые решения неравенства: - 4, -3, -2, -1, 0, 1, 2, 3, 4.
Ответ: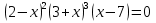
№2 Решить неравенство ![]()
Решение. Преобразуем неравенство следующим образом: ![]()
![]()
![]() . Числитель и знаменатель нужно разложить на множители, для этого их приравняем к нулю:
. Числитель и знаменатель нужно разложить на множители, для этого их приравняем к нулю: ![]() ,
,![]() . Корни первого уравнения 2 и 3. Второе уравнение корней не имеет. Значит, числитель раскладывается на множители следующим образом:
. Корни первого уравнения 2 и 3. Второе уравнение корней не имеет. Значит, числитель раскладывается на множители следующим образом: ![]() , а знаменатель на линейные множители не раскладывается. Запишем неравенство в таком виде:
, а знаменатель на линейные множители не раскладывается. Запишем неравенство в таком виде: ![]() . Отмечаем на числовой прямой точки
. Отмечаем на числовой прямой точки ![]() и
и ![]() и выбираем нужные промежутки.
и выбираем нужные промежутки.
![]()
Ответ: (2;3).
Лист самопроверки к карточке 2.
№1 Решить неравенство ![]()
Решение. Пункты 1), 2), 3) уже выполнены. Отмечаем на числовой прямой точки![]() . При
. При ![]() выражение отрицательно, положительны все сомножители, кроме одного:
выражение отрицательно, положительны все сомножители, кроме одного: ![]() При переходе через точки
При переходе через точки ![]() знак выражения меняется (линейные сомножители в нечетной степени), а при переходе через точку
знак выражения меняется (линейные сомножители в нечетной степени), а при переходе через точку![]() знак не меняется (особая точка).
знак не меняется (особая точка).
![]()
Включаем в ответ все промежутки, на которых левая часть неравенства отрицательна.
Ответ: ![]()
№2 Решить неравенство ![]()
Решение. Числитель и знаменатель нужно разложить на множители, для этого их приравняем к нулю: ![]() ,
,![]() . Корни первого уравнения -1 и -6, второе уравнение имеет один корень -2. Но правильнее в данном случае говорить, что оно имеет два одинаковых корня, поэтому, данный квадратный трехчлен разлагается на два одинаковых сомножителя
. Корни первого уравнения -1 и -6, второе уравнение имеет один корень -2. Но правильнее в данном случае говорить, что оно имеет два одинаковых корня, поэтому, данный квадратный трехчлен разлагается на два одинаковых сомножителя![]() . В этом случае, что уравнение имеет корень чётной кратности. Получаем: -
. В этом случае, что уравнение имеет корень чётной кратности. Получаем: - ![]() . Отмечаем на числовой прямой точки: -6, -2, -1.
. Отмечаем на числовой прямой точки: -6, -2, -1.
![]()
Расставим знаки, учитывая, что при ![]() выражение отрицательно, а при переходе через точку -2 знак не меняется. Остается выбрать нужные промежутки.
выражение отрицательно, а при переходе через точку -2 знак не меняется. Остается выбрать нужные промежутки.
Ответ: (-6;-2)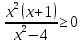 (-2;-1).
(-2;-1).
Лист самопроверки к карточке 3.
№1 Решить неравенство ![]()
Решение. Числитель и знаменатель нужно разложить на множители, для этого их приравняем к нулю: ![]() ,
,![]() . Первое уравнение имеет два одинаковых корня, -1, корни второго уравнения -2 и 3.Разкладываем числитель и знаменатель на множители:
. Первое уравнение имеет два одинаковых корня, -1, корни второго уравнения -2 и 3.Разкладываем числитель и знаменатель на множители: ![]() ,
,
![]() .
.
Получаем неравенство: ![]() . Отмечаем на числовой прямой "выколотые" точки -2 и 3 и особую точку -1.
. Отмечаем на числовой прямой "выколотые" точки -2 и 3 и особую точку -1.
![]()
Расставим знаки, учитывая, что при![]() выражение положительно, а при переходе через точку -1 знак не меняется. Не забудем включить в ответ особую точку -1. Ответ:
выражение положительно, а при переходе через точку -1 знак не меняется. Не забудем включить в ответ особую точку -1. Ответ: ![]()
№2 Решить неравенство ![]()
Решение. Переносим все члены неравенства в левую часть и приводим к общему знаменателю. После приведения подобных членов получаем следующее дробно-рациональное выражение: ![]()
Раскладывая числитель на множители, получим: ![]() .
.
Теперь отмечаем на числовой прямой точки: -2, ![]() ,
, ![]() ,
, ![]() ,
, ![]() нули знаменателя, "выколотые" точки, нули числителя, так как неравенство нестрогое.
нули знаменателя, "выколотые" точки, нули числителя, так как неравенство нестрогое.
При![]() >5 выражение положительно. Так как все сомножители первой степени, то знак меняется во всех точках.
>5 выражение положительно. Так как все сомножители первой степени, то знак меняется во всех точках.
![]()
Осталось выбрать нужные промежутки.
Ответ: ![]()
Лист самопроверки к карточке 4.
№1 Решить неравенство ![]()
Запишем неравенство в виде ![]() ,
,
![]()
Рассмотрим функцию: ![]()
Найдём нули функции, решив уравнение ![]()
![]()
![]()
Ответ: ![]()
№2 Решить неравенство ![]()
Решение. Перенесем все в левую часть и приведем к общему знаменателю, разложив предварительно квадратные трехчлены на сомножители: ![]() и после преобразований получим
и после преобразований получим ![]() . Отметим нули числителя и знаменателя на числовой прямой: точки 0 и 4 - «заштрихованные», точки -1,-3, и 2 - "выколотые". Расставим знаки, учитывая, что на самом правом промежутке левая часть положительна, и знак меняется во всех отмеченных точках, кроме -1.
. Отметим нули числителя и знаменателя на числовой прямой: точки 0 и 4 - «заштрихованные», точки -1,-3, и 2 - "выколотые". Расставим знаки, учитывая, что на самом правом промежутке левая часть положительна, и знак меняется во всех отмеченных точках, кроме -1. ![]()
Ответ: ![]() U
U![]() U
U![]()
Разноуровневая домашняя работа по теме «Решение рациональных и дробно-рациональных неравенств».
(вариант А).
Решите следующие неравенства:
1. (6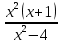 )(х+4)
)(х+4)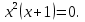 Ответ:
Ответ: 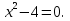
2. (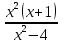 )(
)(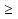 )
)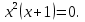 Ответ: (-4;-1)
Ответ: (-4;-1)
3. (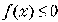 )(
)(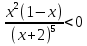 )(х - 1)
)(х - 1)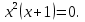 Ответ:
Ответ: 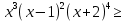
4. (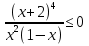 ) (
) (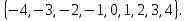 )
)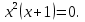 Ответ: (4; 6,5)
Ответ: (4; 6,5)
5. 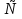 Ответ:
Ответ: 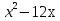
(вариант В).
Решите следующие неравенства:
1. 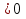 Ответ: [-
Ответ: [-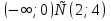 ]
]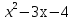
2. 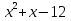 Ответ: {2}.
Ответ: {2}.
3.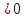 Ответ:
Ответ: ![]() .
.
4. 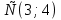 Ответ:
Ответ: 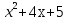
5. 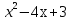
Ответ: (-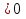
6. 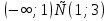 Ответ:
Ответ: ![]()
7. 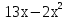 Ответ:
Ответ: ![]()
8. 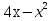 Ответ:
Ответ: ![]()
Упражнения для самостоятельного решения.
-
(
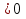 Ответ: [-2;1] U [-2; +
Ответ: [-2;1] U [-2; +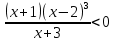
-
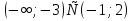 Ответ: (-2;-1) U (-1;1) U(3; +
Ответ: (-2;-1) U (-1;1) U(3; +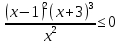
-
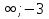 Ответ: (-∞;1] U(2;4]
Ответ: (-∞;1] U(2;4]
-
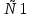 Ответ:
Ответ: 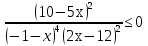
-
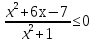 Ответ: (-5;-1) U(1; +
Ответ: (-5;-1) U(1; +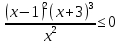
-
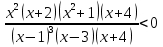 Ответ:
Ответ: 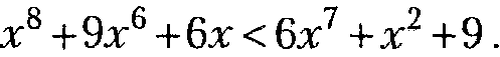
-
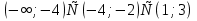 +
+ 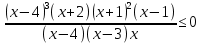 Ответ: [-
Ответ: [-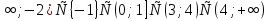 ) U
) U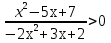
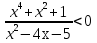
-
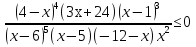 Ответ: (-2;-1] U[2;3)
Ответ: (-2;-1] U[2;3)
-
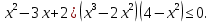 Ответ: х
Ответ: х (- 2;3)
(- 2;3)
-
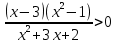 Ответ: х
Ответ: х (-∞; - 6) U [-
(-∞; - 6) U [-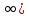 ;1) U [1,5;
;1) U [1,5;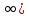 ] U [7;+ ∞).
] U [7;+ ∞).
-
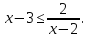 Ответ: х
Ответ: х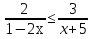
-
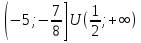 Ответ: х
Ответ: х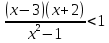
-
 Ответ: x
Ответ: x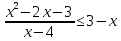
-
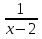 Ответ:
Ответ: 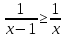
-
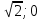 Ответ:
Ответ: 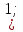
-
 Ответ: x
Ответ: x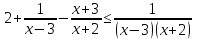
-
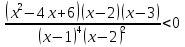 Ответ:
Ответ: 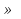
-
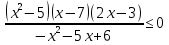 Ответ:( - 7; - 1];{2}
Ответ:( - 7; - 1];{2}
Контрольный тест по теме «Решение рациональных и дробно-рациональных неравенств».
№
Задания
Варианты ответов
Наименьшее целое решение неравенства![]() равно
равно
1) 0; 2) 1; 3) 2; 4) -2; 5) -3
Количество целых отрицательных чисел, не являющихся решениями неравенства![]() равно
равно
1) 1; 2) 2; 3) 3; 4) 5; 5) 6
Среднее арифметическое целых чисел, не удовлетворяющих условию![]() равно
равно
1)-1,5; 2)-3; 3)3; 4)4,5; 5)18
Длина отрезка, являющегося решением неравенства![]() равна
равна
1) 3; 2) 6; 3) 6 - 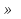 ; 4)
; 4) 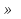 ; 5)
; 5) 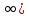
Среднее арифметическое неположительных решений неравенства![]() равно
равно
1)-3; 2)-1,5; 3)-1; 4)-2; 5)-0,5
Количество отрицательных решений неравенства ![]() равно
равно
1) 14; 2) 11; 3) 3; 4) 1; 5) 2
Количество целых решений неравенства ![]() равно
равно
1) 6; 2) 7; 3) 4; 4) 2; 5) 14
Количество целых неотрицательных решений неравенства ![]() равно
равно
1) 2; 2) 1; 3) 13; 4) 4; 5) 11
Количество целых неотрицательных чисел, не принадлежащих области определения функции ![]() равно
равно
1) 8; 2) 4; 3) 1; 4) 3; 5) 2
Количество целых чисел, не принадлежащих области определения функции ![]()
равно
1) 6; 2) 5; 3) 4; 4) 3; 5) 10
Ответы
Номер задания
1
2
3
4
5
6
7
8
9
10
Номер правильного ответа
2
3
1
5
3
5
1
2
4
3
3. Проверочная работа (в одном варианте).
-
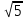 . Ответ:
. Ответ: 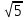
-
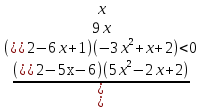 Ответ:
Ответ: 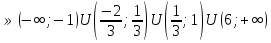
-
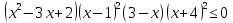 Ответ:
Ответ: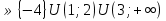
-
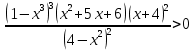
-
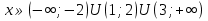 Ответ: (3,5; 4)
Ответ: (3,5; 4)