Равносильность неравенств(Решение ключевых задач)

Урок алгебры (под редакцией А.Г. Мордковича, 2013) в 11 классе по теме "Равносильность неравенств"(базовый уровень)

Урок 2: Решение ключевых задач

Тип урока: урок обобщения, систематизации и совершенствования знаний.

Оборудования: учебники, блокноты, интерактивная доска, карточки с заданиями.

Цели и задачи урока

Цели :

• Повторить основные понятия темы;

• Проанализировать процесс решения неравенств и обосновать цепочку переходов от исходного неравенства к равносильному;

• Способствовать познавательной активности учащихся при помощи информационных технологий;

• Создавать условия для реализации творческих способностей учащихся.

Задачи:

- Создать условия для повторения, закрепления и углубления знаний , при выполнении заданий, связанных с решением уравнений и неравенств, равносильных системам, при отработке основных методов решения, для развития логического мышления .

- Способствовать развитию познавательных и исследовательских умений учащихся, повышению культуры общения.

- Способствовать развитию у учащихся навыков взаимоконтроля и самоконтроля знаний, навыков самостоятельной работы и самостоятельного выбора вида деятельности.

Ход урока

1. Организационный момент (сообщение темы и цели урока).

Приветствие, проверка отсутствующих в классе. Проверка выполнения домашнего задания. Как справились с домашним заданием? Что вызвало затруднение?

2. Актуализация знаний учащихся

• какие неравенства называются равносильными?

• перечислите основные равносильные преобразования.

• с какими равносильными преобразованиями мы познакомились на прошлом уроке?

• преобразования, приводящие к уравнению-следствию.

• что называют решением системы?

• что значит равносильность уравнения (неравенства) системам?

3. Закрепление нового материала.

Начнем, с определения равносильных неравенств:

Опр.: Неравенства (1) и (2) называются равносильными, если их решения совпадают.

(Первый пример решаем всем классом на доске, а второе и третье уравнения по вариантам - два ученика работают у доски)

Пример 1.

1.

2.

Множества решений совпадают. Значит:

Пример 2

1.

«Решение»:

«Ответ»: ( - частные решения)

Проблема в умножении на Он мог быть и отрицательным, и положительным. Надо менять знак.

Правило: в неравенствах нельзя умножать на , если его знак не известен.

2.

Решение:

Ответ: (верно)

Правильное решение:

3.

1.

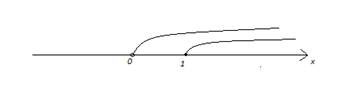
Рис. 1. Иллюстрация к примеру 1

2.

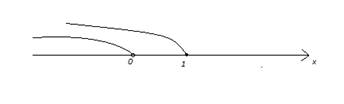
Рис. 2. Иллюстрация к примеру 2

Ответ:

Пример 3.

Решение. На сей раз обе части неравенства всегда неотрицательны, так что возведение в квадрат дает неравенство, равносильное исходному на его естественной области определения. Возведение в квадрат дает неравенство: , (8) область определения дает неравенства: (9) и (10).

Мы не учитываем (10), т.к. если правое, меньшее, подкоренное выражение неотрицательно, то левое и подавно неотрицательно. Стало быть, из неравенства следует такая система:

, возведенное в кв. неравенство и неотрицательность меньшей части.

Неравенство равносильно системе:

Так же рассмотрим равносильные преобразования неравенств

Неравенство 3x2+3,6x≤0,84 равносильно неравенству 3x2+3,6x−0,84≤0,

0,84 перенесли из правой части неравенства в левую с противоположным знаком;

Неравенство 4x2−14x+12≥0 равносильно неравенству 2x2−7x+6≥0,

обе части первого неравенства разделили на положительное число 2;

Неравенство −2x2+7x−6>0 равносильно неравенству 2x2−7x+6<0,

обе части первого неравенства умножили на отрицательное число −1,

при этом знак неравенства > изменили на противоположный, т.е. <;

Неравенство (2t2+3)(7t−6)>0 равносильно неравенству 7t−6>0,

обе части исходного неравенства разделили на выражение 2t2+3,

положительное при любых значениях t, при этом знак исходного неравенства оставили без изменения;

Неравенство 11z+6−2z2−3<0 равносильно неравенству 11z+6>0,

обе части исходного неравенства умножили на выражение −2z2−3

отрицательное при любых значениях z, при этом знак исходного неравенства < изменили на противоположный >.

4. Задания для самостоятельного решения (самостоятельная работа).

1. ]</</p>

2. 

3. 

5. Подведения итогов

Мы рассмотрели важное понятие равносильности неравенств. На следующем уроке рассмотрим метод интервалов. Написали самостоятельную работу, результаты которой сообщу на следующей паре.

6. Домашнее задание

1. Решить неравенства:
   
   а)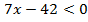
   
   б)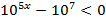

2. Решить неравенства:
   
   a) ;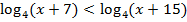
   
   б) ;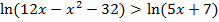

3. Алгебра и начала анализа, Мордкович А.Г.: № 1745, 1746, 1747.