- Учителю
- План-конспект урока по алгебре 8 класс. 'Решение квадратных уравнений'
План-конспект урока по алгебре 8 класс. 'Решение квадратных уравнений'
План-конспект урока по алгебре
Учитель: Паксеева Н.В.
Тема: Решение квадратных уравнений
Класс: 8
Цели урока:
-
Систематизировать знания по теме «Квадратные уравнения».
-
Продолжить работу над формированием следующих математических умений:
-
Решение неполных квадратных уравнений;
-
Решение квадратных уравнений выделением квадрата двучлена;
-
Решение текстовых задач;
-
Умение решать уравнения графически и аналитически;
-
Создать условия контроля (самоконтроля, взаимоконтроля).
3.Воспитывать аккуратность, культуру и организацию труда;
4.Содействовать воспитанию интереса к математике
Оборудование: набор карточек (КИМ), карточки ответов, магнитная доска, карточки с заданиями, таблица с формулами.
Тип урока: Обобщение знаний умений и навыков по теме: «Квадратные уравнения»
Ход урока
1. Организационный момент.
-
определение целей и задач урока;
-
план организации учебной деятельности;
-
задание на дом. (п 19-23, № 643(д,е), 664, 564).
Для желающих задание индивидуальное:
1.Один из корней квадратного уравнения ax![]() +bx+c=0 равен -
+bx+c=0 равен -![]() . Определите с.
. Определите с.
(Сумма корней уравнения равна -![]() . Значит, х
. Значит, х![]() =0; с=0).
=0; с=0).
2.В квадратном уравнении 3х![]() +вх+15=0 найдите в, если известно, что корни уравнения - целые числа.
+вх+15=0 найдите в, если известно, что корни уравнения - целые числа.
(Произведение корней равно 5. Два целых числа в произведении могут дать 5, если : 1) одно из них равно 5, а другое 1 и 2) если одно -5, а другое -1.)
2.Актуализация опорных знаний
-
Индивидуальная работа
а)Решите уравнение (х-2)![]() =3х-8 (2 ученика решают на отворотах доски).(D=1, х
=3х-8 (2 ученика решают на отворотах доски).(D=1, х![]() =4 х
=4 х![]() =3);
=3);
б)Два слабоуспевающих ученика работают по карточкам на первых партах.
Для слабоуспевающих работа по карточкам (решение по образцу)
Алгоритм решения квадратного уравнения
Решить квадратное уравнение
-
Найдите коэффициенты квадратного уравнения
-
Найдите дискриминант квадратного уравнения
-
Найдите корни квадратного уравнения
-
Запишите ответ
2![]() +5х-7=0;
+5х-7=0;
а= , b= , c= .
D=b![]() -4ac
-4ac
D=
![]() , x
, x![]() =
=
![]() , x
, x![]() =
=
Ответ:
Если вы хорошо справляетесь с решением простейших квадратных уравнений, то решите уравнение
![]()
Решение на «3»:D=81, х![]() =1 х
=1 х![]() =-3
=-3![]() ;
;
Решение на «5»: х![]() =1 х
=1 х![]() =-13.
=-13.
2) Устная работа
а) Какие уравнения называются квадратными? (неполные квадратные уравнения, приведённые квадратные уравнения).
б) Назовите алгоритм решения квадратного уравнения (учащиеся, называя алгоритм решения квадратного уравнения, открывают таблицы).
ax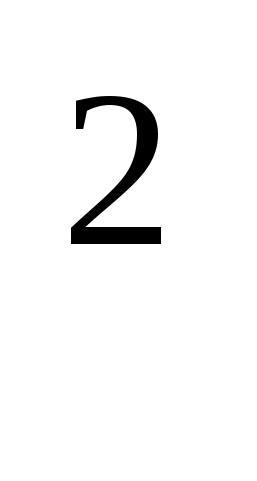 +bx+c=0
+bx+c=0
ax![]() +2kx+c=0
+2kx+c=0
D=b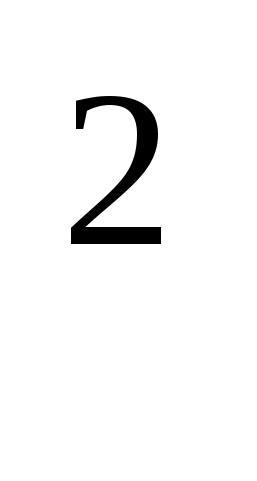 - 4ас
- 4ас
D1=k![]() - ас
- ас
D>0
![]()
![]()
D1>0
![]()
D=0
D<0
Корней
нет
D1=0
D1<0
Корней
нет
Теорема Виета
x![]() +px+q=0
+px+q=0
x![]() x
x![]() =q
=q
x![]() +x
+x![]() =-p
=-p
в) Определите сколько корней имеет квадратное уравнение
2х![]() -5х+10=0 (-); х
-5х+10=0 (-); х![]() +2х-3=0(2); х
+2х-3=0(2); х![]() -4х+4=0(1).
-4х+4=0(1).
г) Найдите второй корень квадратного уравнения, если известен первый корень
д) х![]() -2х-3=0 (х=-1); х
-2х-3=0 (х=-1); х![]() -7х+10=0 (х=5); х
-7х+10=0 (х=5); х![]() +3х-18=0 (х=-6); х
+3х-18=0 (х=-6); х![]() +12х+32=0 (х=-4).
+12х+32=0 (х=-4).
е) Решите квадратное уравнение методом подбора корней
х![]() -11х+28=0 (4;7), х
-11х+28=0 (4;7), х![]() -12х-28=0 (14; -2), х
-12х-28=0 (14; -2), х![]() -8х-20=0 (10;-2).
-8х-20=0 (10;-2).
ж) Установите связь между каждым квадратным уравнением и способами его решения, которые на ваш взгляд, являются наиболее рациональными.
1.ax2 + bx +c = 0;
1.x1 + x2 = -p и x1 · x2 = q
2.ax2 + 2кx +c = 0;
2.![]()
3.аx2 + bx = 0;
3.![]()
4.ax2 + c = 0
4.х![]() =0, х
=0, х![]() =
=![]()
5.ax2 = 0;
5.![]()
6.x2 +px +q, где p и q - целые числа
6.х=0
з) Дети проверяют решение учащихся, работающих индивидуально.
3.Тренировочные упражнения.
-
Решите уравнение 5(х-2)=(3х+2)(х-2). (D=1, х1=1, х2=2)
-
Один из корней данного квадратного уравнения равен -3. Найдите коэффициент k и второй корень уравнения.
5х![]() +kх-12=0
+kх-12=0
-
Решите задачу с помощью квадратного уравнения.
Фотографическая карточка размером 12 на 18см наклеена на лист так, что получилась рамка одинаковой ширины. Определите ширину рамки, если известно, что фотокарточка вместе с рамкой занимает площадь 280 см![]() .
.
4.Рефлексия
Мы изучили тему «Квадратные уравнения».
А сейчас, закройте глаза и представьте себе ясный день. Если ваши знания хорошие по данной теме, то пусть день останется ясным, если что - то осталось непонятным - небольшое облако заслонит солнце, солнечное затмение будет у того, кто плохо знает данную тему.
Поднимите руки те, у кого произошло солнечное затмение. А сейчас те, у кого продолжает светить солнце.
5.Самостоятельная работа в виде теста
А1. Какое из уравнений является квадратным?
1.3х+4=0
2.х![]() +3х+5=0
+3х+5=0
3.х![]() -5х
-5х![]() +2х-3=0
+2х-3=0
А2. Какое из уравнений является приведённым?
1.3х![]() -2х+5=0
-2х+5=0
2.-2х![]() -7+3х=0
-7+3х=0
3. х![]() +6х-4=0
+6х-4=0
А3.Назовите коэффициенты квадратного уравнения
4х-3х![]() +1=0.
+1=0.
1.а=4; b=-3; с=1
2. а=-3; b=4; с=1
3. а=1; b=-3; с=4
А4. Найдите сумму корней квадратного уравнения х![]() -16х+28=0.
-16х+28=0.
1.16
2.28
3.-16
А5. Найдите произведение корней квадратного уравнения х![]() -12х-45=0.
-12х-45=0.
1.-12
2.45
3.-45
В1.3х![]() -12х=0
-12х=0
В2.х![]() -х-2=0
-х-2=0
С3.Периметр прямоугольника равен 20см. Найдите стороны прямоугольника, если известно, что площадь прямоугольника равна 24см![]()
А1. Какое из уравнений является квадратным?
1.3х+4=0
2. х![]() +3х
+3х![]() +2х
+2х![]() -3х=0
-3х=0
3. -2х![]() -4х-3=0
-4х-3=0
А2. Какое из уравнений является приведённым?
1.х![]() -5х+8=0
-5х+8=0
2.-6х![]() -9+3х=0
-9+3х=0
3.5 х![]() -6х-1=0
-6х-1=0
А3.Назовите коэффициенты квадратного уравнения х+3х![]() -4=0.
-4=0.
1.а=1; b=3; с=-4
2. а=3; b=4; с=1
3. а=3; b=1; с=-4
А4. Найдите сумму корней квадратного уравнения х![]() +17х+60=0.
+17х+60=0.
1.17
2.60
3.-17
А5. Найдите произведение корней квадратного уравнения х![]() +3х-40=0.
+3х-40=0.
1.3
2-40
3.40
В1.5х![]() +15х=0
+15х=0
В2.2х![]() -3х-2=0
-3х-2=0
С3.Периметр прямоугольника равен 30см. Найдите стороны прямоугольника, если известно, что площадь прямоугольника равна 56см![]()
Ответы оформляются на бланках ответов (Ответы задания А отмечаются крестиком в нужной ячейке, задания В - ответ, С - полное решение )
№
А1
А2
А3
А4
А5
1
2
3
В1
В2
С1
5.Подведение итогов
Образовательные цели урока:
-
Повторить формулы корней неполных квадратных уравнений.
-
Исследовать зависимость между коэффициентами и корнями квадратного уравнения.
-
Познакомить учащихся с теоремой Виета.
-
Выявить каким образом теорема Виета может быть применима при решении квадратных уравнений.
-
Начать формировать у учащихся умение применять теорему Виета при решении квадратных уравнений.
Развивающие цели урока:
-
Развивать и совершенствовать умение применять имеющиеся у учащихся знания в новой ситуации.
-
Способствовать развитию умения определять черты сходства и различия в изучаемых объектах.
-
Способствовать развитию умения делать выводы и обобщения.
Воспитательные цели урока:
-
Способствовать выработке у школьников желания и потребности изучаемых фактов.
-
Воспитывать самостоятельность и творчество.
-
Используя исторический материал, повышать интерес к изучению математики.
Ход урока
I. Организационный момент.
II. Актуализация знаний.
Д/з учащихся включало в себя задание: придумать приведенное квадратное уравнение с целыми корнями, решить его, записать на альбомном листе крупно данное квадратное уравнение, на втором листе - корни этого уравнения.
Учитель предлагает учащимся показать приготовленные уравнения и быстро решает их, называя корни, вызывая удивление учащихся. Затем она приглашает фокусника из числа учащихся (заранее подготовленный ученик), который по корням квадратных уравнений угадывает придуманные учащимися уравнения.
Далее учитель сообщает учащимся, что такие фокусы они тоже смогут показывать, если будут внимательны и активны на уроке.
III. Повторение пройденного материала.
(Два ученика работают с таблицей у доски.) Задание: заполнить пустые места в таблице.
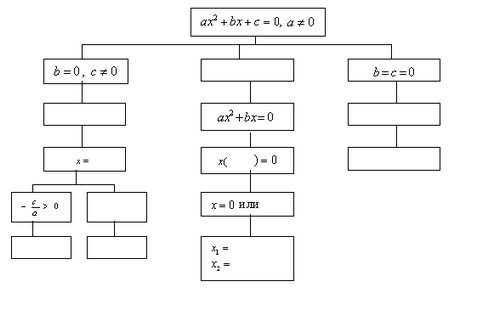
Рисунок 1
(Остальная часть класса разгадывает кроссворд, используя теоретические знания)
Задание: если вписать верные слова, то в выделенной строке получится фамилия французского математика.
Вопросы:
1. Квадратное уравнение с первым коэффициентом равным 1 (приведенное).
2. Подкоренное выражение в формуле корней квадратного уравнения (дискриминант).
3. Один из видов квадратного уравнения (неполное).
4. a, b в квадратном уравнении (коэффициенты).
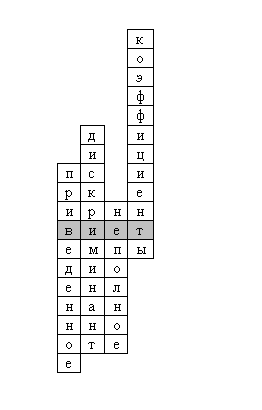
В выделенной строке получится фамилия французского математика Виета.
IV. Историческая справка (сообщение учащегося о жизни и деятельности математика Франсуа Виета или презентация).
Цель: Сегодня на уроке мы исследуем зависимость между коэффициентами и корнями квадратного уравнения.
-
Занимаясь квадратными уравнениями, вы, вероятно, уже заметили, что информация об их корнях скрыта в коэффициентах. Кое-что для нас уже открылось. От чего зависит наличие или отсутствие корней квадратного уравнения? (от дискриминанта)
-
Из чего составляется дискриминант квадратного уравнения? (из коэффициентов a, b, c)
-
В зависимости от того, каковы коэффициенты квадратного уравнения, можно определить корни неполных квадратных уравнений, проверяем заполнение учащимися таблицы.
Как ещё связаны между собой корни и коэффициенты квадратного уравнения? Чтобы раскрыть эти связи, наверное, будет полезно понаблюдать за коэффициентами и корнями различных квадратных уравнений. При поиске закономерностей исследователи часто фиксируют свои наблюдения в таблицах, которые помогают обнаружить эти закономерности. (Учащийся от каждого ряда решает задание на доске, а остальные выполняют задание в тетради.)
Задание. Решить уравнение.
I ряд
3(x2 2) x = 2x2
3x2 6 x 2x2=0
x2 x 6=0
D = 25
x1 = 3
x2 = 2
II ряд
![]()
4(3x + 3) =2(1 x2)
2x2 + 12x + 10 = 0
x2 + 6x + 5 = 0
D1 = 4
x1 = 1
x2= 5
III ряд
(x 3)2 = 1
x2 + 9 6x = 1
x2 6x + 8 = 0
D1 = 1
x1 = 4
x2 = 2
Дополнительно
(x 1)(x + 2) + 3x = 10
x2 + x 2 + 3x 10 = 0
x2 + 4x 12 = 0
D1 = 16
x1 = 2
x2 = 6
Давайте посмотрим, какова зависимость между коэффициентами и корнями приведенного квадратного уравнения.
Задание. Заполнить пропуски в таблице
Уравнение
a
b
c
x1
x2
x1 + x2
x1x2
x2 - x - 6 = 0
x2 + 6x + 5 = 0
x2 - 6x + 8 = 0
x2 + 4x -12 = 0
Помогла ли вам эта таблица в раскрытии новых связей между корнями и коэффициентами квадратных уравнений? Выскажите гипотезу, утверждение (учащиеся делают выводы). Сравните сформулированную вами гипотезу с теоремой, записанной в учебнике.
Теорема: Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. (Прочитать доказательство самостоятельно.)
Теорема называется теоремой Виета по имени знаменитого французского математика Франсуа Виета (1540-1603). Свою знаменитую теорему он доказал в 1591 году.
Итак, тема сегодняшнего урока - "Теорема Виета".
Цель нашего урока: познакомится с теоремой Виета и рассмотреть каким образом она применима к решению квадратных уравнений.
Задание. Используя теорему Виета, заполните пропуски в формулах.
Уравнение
Сумма корней
Произведение корней
x2 - 5x - 6 = 0
x2 - 3x + = 0
2
x2 + x - 10 = 0
-3
x2 + x + = 0
5
-14
Применима ли теорема Виета для квадратного уравнения в общем виде? (Да, если заменить это уравнение равносильным ему приведённым уравнением.)
ax2 + bx + c = 0
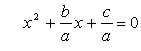
если x1 и x2 - корни данного уравнения, то по теореме Виета:
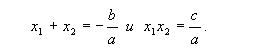
Сформулируйте утверждение для квадратного уравнения в общем виде.
Теорема: Если корни квадратного уравнения ax2+bx+c=0 существуют, то сумма корней равна
![]()
а произведение корней
![]() .
.
"По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи постоянства такого:
Умножишь ты корни - и дробь уж готова.
В числителе c, в знаменателе a,
А сумма корней тоже дроби равна
Хоть с минусом дробь, что за беда,
В числителе b, в знаменателе a."
Задание. Найти сумму и произведение корней квадратного уравнения.
Уравнение
Сумма корней
Произведение корней
а) x2 - 37x + 27 = 0
б) y2 + 41y - 371 = 0
в) x2 - 210x = 0
г) y2 - 19 = 0
д) 2x2 - 9x - 10 = 0
е) 5x2 + 12x + 7 = 0
ж) - z2 + z = 0
з) 3x2 - 10 = 0
В некоторых случаях корни уравнения можно найти подбором. Вспомните начало урока - как быстро я находила корни ваших уравнений. Подбор корней значительно облегчает решение, если известны зависимости между корнями и коэффициентами уравнения. Формулы, выражающие эти зависимости, отражены в теореме Виета.
Попробуем, не решая, найти корни квадратных уравнений.
Учащиеся решают задание № 964-966(а,б), используя данную теорему.
Устно: Не решая данного уравнения, определите какие числа являются корнями уравнения.
x2- 5x + 4 = 0
-1 и -4
x2 + 5x + 4 = 0
-1 и 4
x2 - 3x - 4 = 0
1 и 4
x2 + 3x - 4 = 0
1 и -4
Как вы решали? Мы можем выполнять эту операцию на основании теоремы, обратной теореме Виета. Сформулируйте утверждение, обратное теореме Виета. Что нужно знать для того, чтобы сформулировать обратную теорему?
Теорема. Если действительные числа x1 и x2 таковы, что x1 + x2= - p и x1x2=q, то эти числа являются корнями квадратного уравнения x2 + px + q = 0.
Рассмотрим, в каких случаях применяют теорему Виета и обратную ей теорему.
1) Теорему, обратную теореме Виета, можно использовать для проверки, найденных корней квадратного уравнения. Рассмотрим задания из домашней работы № 951(в), 952(г).
в) 9х2 + 30х - 11=0
х1= -11/3 , х2 =1/3
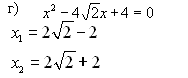
По теореме Виета:

Проверяем:

2) Теорему, обратную теореме Виета используют также при составлении квадратных уравнений. Вспомните фокусника, который, зная корни, угадывал ваши квадратные уравнения.
Пусть
-
х1=2, х2=5, составьте квадратное уравнение (х2-7х+10=0),
-
х1=- 4, х2=3, составьте квадратное уравнение (х2+х-12=0),
-
х1= - 6, х2= -10, составьте квадратное уравнение (х2+16х+60=0).
Но чаще всего эту теорему используют для нахождения корней методом подбора.
V. Итог урока:
а) Самостоятельная работа (разноуровневая).
-
Решите уравнение и выполните проверку по теореме, обратной теореме Виета: х2-2х-24=0.
-
Найдите подбором корни уравнения х2+3х-28=0.
-
Один из корней данного уравнения равен 2. Найдите второй корень и коэффициент а: х2-ах-12=0
б) С какими теоремами вы познакомились сегодня на уроке? В каких ситуациях может быть применима теорема Виета и ей обратная теорема?
Домашнее задание: § 24, № 964-965(в,г), 967(в,г), 985(в,г), 990(в,г).