Урок по алгебре в 9 классе «Применение основных тригонометрических формул к преобразованию выражений»

Урок по алгебре в 9 классе

Тема «Применение основных тригонометрических формул к преобразованию выражений».

Цели урока: систематизация и обобщение изученного материала путём решения упражнений.

Задачи:

Образовательные:

• закрепить и проверить зун учащихся при решении разнообразных упражнений с использованием тригонометрических формул;

• применять свои знания в практических ситуациях.

Развивающие:

• развивать мышление, математическую речь, навыки самостоятельной работы.

Воспитательные:

• повысить интерес к предмету; воспитывать положительный мотив учения;

• формировать отношения взаимной ответственности при совместной работе.

Тип урока. Урок систематизации и обобщения знаний.

Форма проведения: фронтальная, парная, коллективная.

Оборудование на уроке: интерактивная доска, карточки с заданиями, тест, карточки для рефлексии, презентация, справочный материал для слабых учащихся.

Структура урока:

1. Подготовительный этап ( мотивация повторения, выявление целей урока и ориентация учащихся в учебной деятельности на уроке).

2. Актуализация ЗУН

3. Решение упражнений

4. Тестирование

5. Подведение итогов урока и домашнее задание

6. Рефлексия

ХОД УРОКА

1. Организационно-мотивационный момент.

Сегодня повторим формулы основных тригонометрических тождеств и систематизируем знания и умения, применяя формулы при преобразовании тригонометрических выражений. Задания на тригонометрию есть на ВОУДе и ЕНТ, поэтому нам предстоит поработать и с формулами, решая упражнения и выполнить тест.

Слайды 1,2,3

Высказывание «У математиков существует свой язык-это формулы».

С.Ковалевская

На столах листы для оценивания, ознакомьтесь. Подпишите. Не забывайте их заполнять, чтобы в конце урока вывести итоговую оценку.

Устная работа на уроке

Работа по карточке

тест

итоговая оценка за урок

2. Актуализация знаний учащихся.

Цель: повторение теоретического материала, подготовка учащихся к работе на уроке.

Слайды 4-12

Фронтальный опрос.

• Дописать тригонометрические тождества и вывести следствия:

А) Основные тригонометрические тождества

sin²+cos²=1

tg  ctg =1

tg =

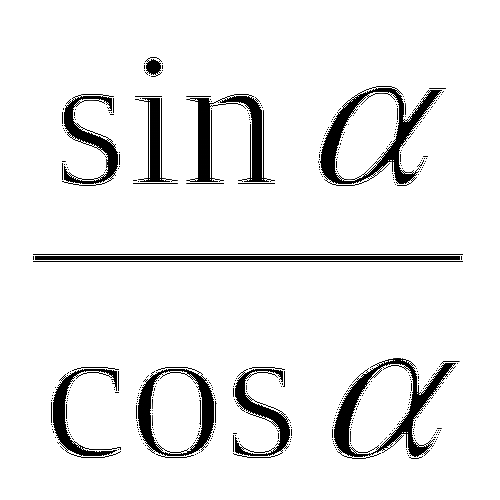
tg²+1=

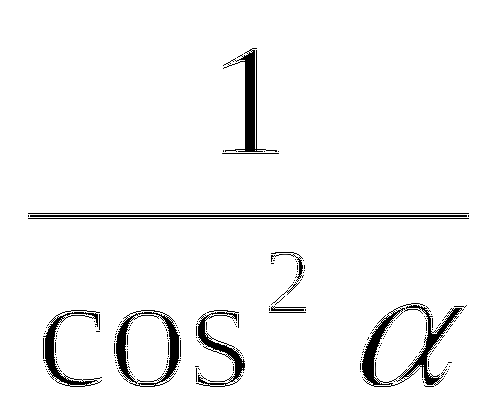
ctg =

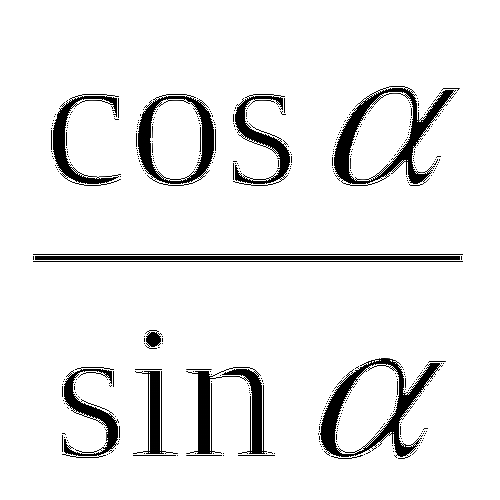
ctg²+1=

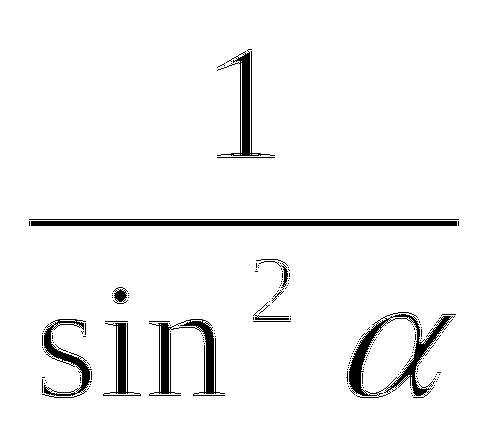
Б) Следствия из основных тригонометрических формул

sin = 

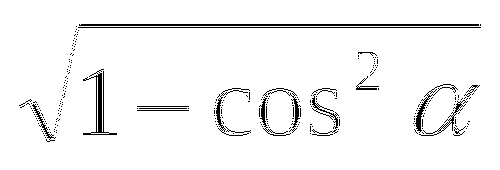
cos = 

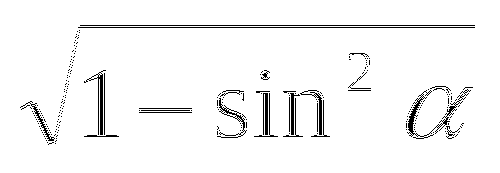
tg =

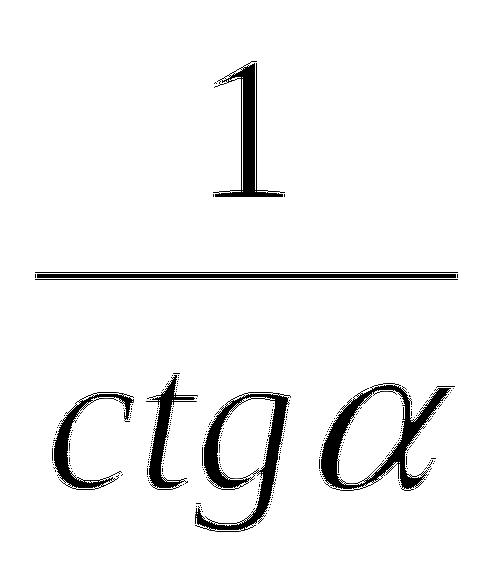
ctg =

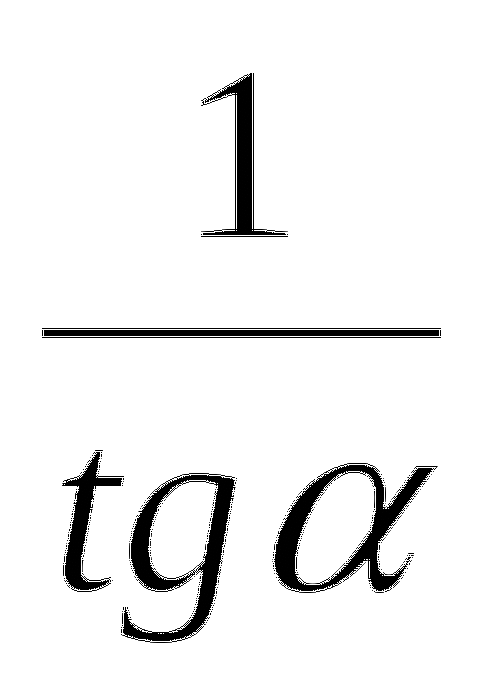
cos²=

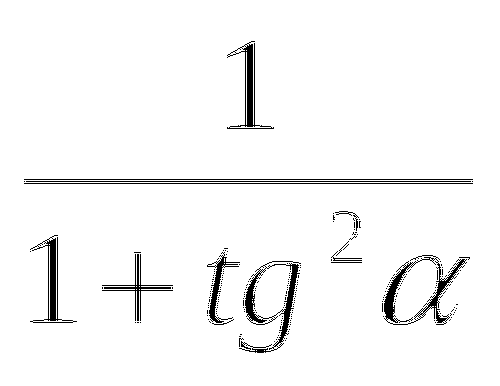
sin²=

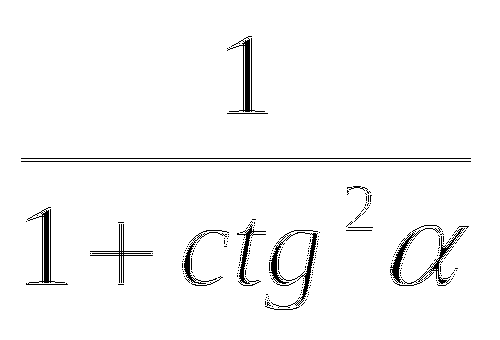
• Определите четверть:

90°<α<180° (2 чет)

3π/2<α<2π (4 чет)

0°<α<90° (1 чет)

π<α<3π/2 (3 чет)

• Какие знаки имеют тригонометрические функции в каждой из координатных четвертях?

(знаки тригонометрических функций)

четверть

функция

sin

cos 

tg 

ctg 

I

+

+

+

+

II

+

-

-

-

III

-

-

+

+

IV

-

+

-

-

Устное решение упражнений.

• Упростите выражение:

cos² 23°+sin² 23° (1)

(sin α+1)(1-sin α) (cos²α)

sin α·ctg α (cos α)

tg α·cos α (sin α)

1+(cos²α/sin²α) (1+ сtg²α)

sin²α/cos α (tg α sin α)

-tg 17°·ctg 17° (-1)

3. Решение упражнений.

Цель: систематизация знаний и умений.

Слайды 13-15

Часть учащихся работают самостоятельно на местах по карточкам.

Самостоятельная работа

Вариант 1

1.Найди sinα и tg α, если известно, что cos α=8/17 и 3π/2<�����������������

���������������������

����������������������

�����������

�����������������

������������������

��������

�������������������

����т 2

1.Найди cos α и сtg α, если известно, что sin α=12/13 и 0<���������������

���������������������

����������������

tg α 1+cos α

3.Докажи тождество: 1

------- - 1 = сtg² β .

sin²β

Самостоятельная работа

Вариант 3

1.Найди cos α и сtg α, если известно, что sin α=0,8 и π/2<�������-3/4)

2.Упрости выражение: 1- sin α• cos α• tg α. (cos² α)

3.Докажи тождество: sin²β

---------- • ctg² β = -1 .

sin²β-1

Слабоуспевающие учащиеся выполняют упражнения на доске под контролем учителя. На столах у них справочный материал.

1. Найди cos α и tg α, если известно, что sin α=5/13 и π/2<α<π. (-12/13;-5/12)

2. Упрости выражение:1-ctg α·cos α·sin α. ( sin²α)

3. Докажи тождество: 1/sin β-sin β=cos β·ctg β.

4. Тестирование

Слайды 16-17

Цель: подготовка к ВОУД.

Вариант 1

1. Найти cos α, если известно, что sin α=1/2

А) -1/2

В) √3/2

С) -√3/2

Д) 1/2

Е) 1

2. Упрости: (sin α+ cos α)²+(sin α- cos α)².

А) 0

В) 2

С) -2

Д) -1

Е) 3

3. Упрости: sin² 7° +cos² 7°.

А) 14

В) -1

С) 7

Д) 1

Е) 0

4.Упрости: tg α· ctg α - cos α².

А) 0

В) 1

С) sin² α

Д) - sin² α

Е) cos α²

5. Упрости: 7sin² α +7cos² α-5

А) -12

В) 12

С) 7

Д) 2

Е) 9

Вариант 2

1. Найти sin α, если известно, что cos α =√2/2

А) -√2/2

В) √3/2

С) 2

Д) √2/2

Е) 1

2. Упрости: (1- cos α)(1+ cos α)

А) 0

В) cos α

С) sin α

Д) cos α²

Е) sin² α

3. Упрости: cos² 5° + sin² 5°

А) 10

В) -1

С) 5

Д) 1

Е) 0

4. Упрости: sin² α- ctg α tg α

А) 0

В) -cos α²

С) sin² α

Д) -1

Е) cos α²

5. Упрости: 4sin² α +4cos² α+1

А) 5

В) 7

С) 9

Д) -7

Е) 0

Самоконтроль

Вариант 1 вариант 2

1.в 1.д

2.в 2.е

3.д 3.д

4.с 4.в

5.д 5.а

Критерии оценок: «5»-все задания

«4»-4 задания

«3»-3 задания

5. Подведение итогов.

Итак, сегодня мы в нестандартных комбинированных заданиях повторили и систематизировали знания и умения. (Итоги подводят ученики)

1. Выставление оценок.

2. Домашнее задание: Из сборника пгк решить

вар 7 у25,26;вар 8 у25,26;вар 9 у24

3. Рефлексия:

Слайды 18-19

Заполнение карточек:

На уроке я работал активно/пассивно

Своей работой на уроке я доволен/не доволен

За урок я не устал/устал

Материал урока мне был понятен/не понятен

интересен/скучен

полезен/бесполезен

Слайд 20

Используемая литература:

1.Хамзина Б.Е. и другие «Сборник заданий для проведения письменного экзамена по математике за курс 9-летней общеобразовательной школы». Издательство «Келешек-2030», 2008 г.

2. Симакин М.В. «Тестовые задания по математике 9 класс для ПГК». Издательство «Келешек-2030», 2005 г.

3. Сайт 1september @.ru