- Учителю
- Программа по предпрофильной подготовке для учащихся 9 классов по математике по курсу «Модуль»
Программа по предпрофильной подготовке для учащихся 9 классов по математике по курсу «Модуль»
МОУ Большемурашкинская средняя общеобразовательная школа
Программа по предпрофильной подготовке для учащихся 9 классов по математике по курсу
«Модуль»
Автор программы: Учитель математики высшей категории Житнякова Ольга Сергеевна
Большое Мурашкино 2009
Пояснительная записка
Элективный курс по предпрофильной подготовке учащихся 9 классов посвящении систематическому изложению учебного материала, связанного с понятием модуля числа и аспектами его применения. В нем рассматриваются различные методы решения уравнений и неравенств с модулем, основанные на его определении, свойствах и графической интерпретации. Стоит отметить, что навыки в решении уравнений, неравенств, содержащих модуль и построение графиков элементарных функций, содержащих модуль необходимы любому ученику, желающему не только успешно выступать на математических олимпиадах, но и хорошо подготовиться к поступлению в дальнейшем в высшие учебные заведения. Материал данного курса содержит нестандартные методы, которые позволяют более эффективно решать класс заданий, содержащих модуль. Наряду с основной задачей обучения математики - обеспечением прочного и сознательного овладения учащимися системой математических знаний и умений, данный курс предусматривает формирование интереса к предмету, выявление и развитие математических способностей, ориентацию на профессии, существенным образом связанные с математикой, выбору профиля дальнейшего обучения.
Цели курса:
-
Помочь повысить уровень понимания и практической подготовки в таких вопросах, как:
-
Преобразование выражений, содержащих модуль;
-
Решение уравнений и неравенств, содержащих модуль;
-
Построение графиков элементарных функций, содержащих модуль;
-
Создать в совокупности с основными разделами курса базу для развития способностей учащихся;
-
Помочь осознать степень своего интереса к предмету и оценить возможности овладения с точки зрения дальнейшей перспективы.
Задачи курса:
-
Научить учащихся преобразовывать выражения, содержащие модуль;
-
Научить учащихся решать уравнения и неравенства, содержащие модуль;
-
Научить строить графики , содержащие модуль;
-
Рассмотреть уравнения, неравенства с двумя переменными, содержащие модуль на координатной плоскости ;
-
Помочь ученику оценить свой потенциал с точки зрения образовательной перспективы.
Сроки реализации программы
Данный курс рассчитан на 15 часов , предполагает компактное четкое изложение теории вопроса, решение типовых задач, самостоятельную работу, защиту проектов, тестирование.
Основные принципы отбора и структурирования материала
Включенный в программу материал представляет познавательный интерес для учащихся и может применяться для разных групп школьников вследствие своей обобщенности и практической направленности. Развертывание учебного материала четко структурировано и соответствует задачам курса.
Методы, формы обучения, режим занятий
В программе приводится примерное распределение учебного времени, включающее план занятий.
Каждое занятие состоит из двух частей: задачи, решаемые с учителем и задачи для самостоятельного ( или домашнего) решения. Основные формы организации учебных занятий: лекции, объяснение, практическая работа, семинар, тестирование, творческие задания.
Предполагаемые результаты
Разнообразный дидактический материал дает возможность отбирать дополнительные задания для учащихся разной степени подготовки: уровень сложности задач варьируется от простых до конкурсных и олимпиадных. Все занятия направлены на развитие интереса школьников к предмету, на расширение представлений об изучаемом материале на решение новых и интересных задач.
Программа может быть эффективно использована в 9 классах с любой степенью подготовленности, способствует развитию познавательных интересов, мышления учащихся, представляет возможность подготовиться к сознательному выбору профиля обучения и дальнейшей специализации.
Инструментарий для оценивания результатов
Установление степени достижения учащимися промежуточных и итоговых результатов производится на каждом занятии благодаря использованию
практикумов, самостоятельных работ, тестов, консультаций.
Формой итоговой отчетности учащихся являются проекты.
Учебно - тематический план
Наименование тем курса
Количество часов
Технология реализации
Модуль: общие сведения, преобразование выражений, содержащих модуль
1
Лекция, объяснение, выполнение тренировочных упражнений
Решение уравнений и неравенств, содержащих модуль
3
Объяснение, выполнение тренировочных упражнений
Проверочная работа
1
Проверочная работа
Графики функций, содержащих модуль
3
Лекция, объяснение, выполнение тренировочных упражнений
Тестирование
1
Тестирование
Неравенства с двумя переменными, содержащие модуль на координатной плоскости
3
Объяснение, выполнение тренировочных упражнений
Презентации проектов: «Графики улыбаются», «Метод линейного сплайна», «Неравенства на координатной плоскости»…
2
Семинар
Итоговое тестирование
1
Тестирование
Итого:
15
Содержание изучаемого материала
Тема 1: Модуль: общие сведения, преобразование выражений, содержащих модуль (1 ч)
Занятие 1:Модуль: общие сведения, определение, свойства модуля, преобразование выражений, содержащих модуль .
Методы обучения: лекция, объяснение, выполнение тренировочных упражнений.
Формы контроля: проверка самостоятельно решенных задач.
Тема 2: Решение уравнений и неравенств, содержащих модуль (3ч.)
Занятие 2: Решение уравнений, содержащих модуль (1ч.) Решение уравнений вида:f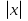 = а,
= а, 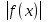 =а,
=а, 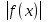 =g (х),
=g (х),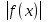 =
=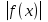 ,
,
Методы обучения: объяснение, выполнение тренировочных упражнений.
Формы контроля: проверка самостоятельно решенных задач.
Занятие 3: Решение неравенств, содержащих модуль (1ч.) Решение неравенств вида:f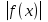 а,
а, 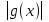 а,
а, 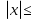 g ( х),
g ( х),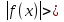 ,
,
Методы обучения: объяснение, выполнение тренировочных упражнений.
Формы контроля: проверка самостоятельно решенных задач.
Занятие 4: Решение уравнений и неравенств, содержащих модуль (1ч.)
Решение уравнений и неравенств, содержащих модуль в модуле. Метод замены переменной. Решение систем уравнений и неравенств, содержащих модуль.
Методы обучения: беседа, объяснение, выполнение тренировочных упражнений.
Формы контроля: проверка самостоятельно решенных задач.
Занятие 5: проверочная работа (1ч.)
Тема 3 : Графики функций, содержащих модули.
Занятие 6: Построение графиков функций, содержащих модуль (1ч.) Построение графиков функций вида :у=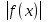 , у=f
, у=f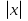 , уравнений
, уравнений 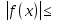 =f(х),
=f(х), 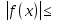 =
=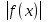 .
.
Методы обучения: лекция, объяснение, выполнение тренировочных упражнений.
Занятие 7: Построение графиков кусочно-линейных функций (1ч.), метод линейного сплайна.
Методы обучения: объяснение, выполнение тренировочных упражнений.
Формы контроля: проверка самостоятельно решенных задач.
Занятие 8: Построение уравнений вида : у=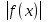 ,
, 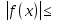 =
=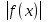 , (1ч)
, (1ч)
Методы обучения: объяснение, выполнение тренировочных упражнений.
Формы контроля: проверка самостоятельно решенных задач.
Занятие 9: тестирование (0.5ч)
Занятие 9-10: неравенства с двумя переменными, содержащие модуль на координатной плоскости (1, 5ч)
Методы обучения: объяснение, выполнение тренировочных упражнений.
Занятие 11: презентация проектов (1ч).
Методы обучения: семинар.
Формы контроля: защита проектов.
Занятие 12: итоговое тестирование (1ч.)
Методические рекомендации
Данный элективный курс «Модуль» дает примерный объем знаний, умений и навыков, которым должны овладеть ученики. Учащиеся должны научиться решать задачи более высокой по сравнению с обязательным уровнем сложности, овладеть рядом технических и интеллектуальных умений на уровне их свободного использования. Одна из целей преподавания данного курса ориентационная - помочь осознать ученику степень значимости своего интереса к математике и оценить свои возможности, поэтому интерес и склонность учащегося к занятиям на курсах должны всемерно подкрепляться и развиваться. В методической литературе немало внимания уделяется данной теме, однако задания с модулем вызывают у учащихся ошибки и затруднения. Одна из причин кроется в непонимании модуля числа. Учитель должен обратить внимание учащихся на то, что число х может быть как отрицательное, так и положительное.
Для построения всех видов графиков учащимся достаточно хорошо понимать определение модуля и знать виды простейших графиков, изучаемых в школе.
Поурочное домашнее задание является обязательным для всех. Активным учащимся можно предлагать творческие задания. Ученики могут работать не только самостоятельно, но и в микрогруппах, в соответствии со своими приоритетами и возможностями.
В результате обучения курса учащиеся должны уметь:
-
точно и грамотно формулировать теоретические положения и излагать собственные рассуждения в ходе решения заданий;
-
применять изученные алгоритмы в ходе решения соответствующих заданий;
-
преобразовывать выражения, содержащие модуль;
-
решать уравнения и неравенства , содержащие модуль;
-
строить графики элементарных функций, содержащих модуль; решать уравнения с двумя переменными на координатной плоскости, содержащими модуль.
Список литературы
-
Математика абитуриенту. В.В. Ткачук.- Москва: Тейс,1994.
-
Математика 8-9класс. Сборник элективных курсов. В.Н. Студенецкая. Волгоград: учитель, 2006.
-
Предпрофильная подготовка учащихся 9 классов по математике. И.Н. Данкова. - Москва: «5» за знание, 2006.