- Учителю
- Рабочая программа по геометрии 7 класс Атанасян по фгос
Рабочая программа по геометрии 7 класс Атанасян по фгос
Муниципальное казенное общеобразовательное учреждение
«Рябинковская основная школа»
на заседании педагогического совета
протокол №______
от «___»__________20___г.
«Согласовано»
Заместитель директора
________Е.А. Ермакова
«_____»_________20___г.
«Утверждаю»
Директор
МКОУ «Рябинковская ОШ»
_______Е.О. Станулевич
«_____»__________20___г.
Рабочая программа
по предмету «геометрия»
класс 7
Составитель: Кошмелюк Е.Е
учитель математики
2015 г.
2.Пояснительная записка.
Рабочая программа основного общего образования составлена на основе Фундаментального ядра содержания общего образования и Требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте основного общего образования. В ней также учитываются основные идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования.
Программа разработана в соответствии с:
-
авторской программой основного общего образования по геометрии (Геометрия. Рабочая программа к учебнику Л.С. Атанасяна и других. 7-9 классы: пособие для учителей общеобразов. учреждений / В.Ф.Бутузов. - М.: Просвещение, 2013. - 31 с.) .
Геометрия является одним из опорных предметов: она обеспечивает изучение других дисциплин. В первую очередь это относится к предметам естественно-научного цикла, в частности к физике. Развитие логического мышления учащихся при обучении геометрии способствует также усвоению предметов гуманитарного цикла. Практические умения и навыки геометрического характера необходимы для трудовой деятельности и профессиональной подготовки школьников.
Развитие у учащихся правильных представлений о сущности и происхождении геометрических абстракций, соотношении реального и идеального, характере отражения математической наукой явлений и процессов реального мира, месте геометрии в системе наук и роли математического моделирования в научном познании и в практике способствует формированию научного мировоззрения учащихся, а также формированию качеств мышления, необходимых для адаптации в современном информационном обществе.
Требуя от учащихся умственных и волевых усилий, концентрации внимания, активности развитого воображения, геометрия развивает нравственные черты личности (настойчивость, целеустремленность, творческую активность, самостоятельность, ответственность, трудолюбие, дисциплину и критичность мышления) и умение аргументировано отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения.
Геометрия существенно расширяет кругозор учащихся, знакомя их с индукцией и дедукцией, обобщением и конкретизацией, анализом и синтезом, классификацией и систематизацией, абстрагированием, аналогией. Активное использование задач на всех этапах учебного процесса развивает творческие способности школьников.
При обучении геометрии формируются умения и навыки умственного труда - планирование своей работы, поиск рациональных путей её выполнения, критическая оценка результатов. В процессе обучения геометрии школьники должны научиться излагать свои мысли ясно и исчерпывающе, лаконично и ёмко, приобрести навыки четкого, аккуратного и грамотного выполнения математических записей.
Важнейшей задачей школьного курса геометрии является развитие логического мышления учащихся. Сами объекты геометрических умозаключений и принятые в геометрии правила их конструирования способствуют формированию умений обосновывать и доказывать суждения, приводить четкие определения, развивают логическую интуицию, кратко и наглядно вскрывают механизм логических построений и учат их применению. Тем самым геометрия занимает ведущее место в формировании научно-теоретического мышления школьников.
Раскрывая внутреннюю гармонию математики, формируя понимание красоты и изящества математических рассуждений, способствуя восприятию геометрических форм, усвоению понятия симметрии, геометрия вносит значительный вклад в эстетическое воспитание учащихся. Её изучение развивает воображение школьников, существенно обогащает и развивает их пространственные представления.
Основные цели курса:
-овладение системой математических знаний и умений, необходимых в практической деятельности, продолжения образования;
-приобретение опыта планирования и осуществления алгоритмической деятельности;
-освоение навыков и умений проведения доказательств, обоснования выбора решений;
-приобретение умений ясного и точного изложения мыслей;
-развить пространственные представления и умения, помочь освоить основные факты и методы планиметрии;
-научить пользоваться геометрическим языком для описания предметов.
Задачи обучения:
-ввести основные геометрические понятия, научить различать их взаимное расположение;
-научить распознавать геометрические фигуры и изображать их;
-ввести понятия: теорема, доказательство, признак, свойство;
-изучить признаки равенства треугольников;
-изучить признаки параллельности прямых и научить применять их при решении задач и доказательстве теорем;
-научить решать геометрические задачи на построение, на доказательства и вычисления;
-подготовить к дальнейшему изучению геометрии в последующих классах.
3.Общая характеристика курса геометрии в 7 классе
В курсе условно можно выделить следующие содержательные линии: «Наглядная геометрия», «Геометрические фигуры», «Измерение геометрических величин», «Логика и множества», «Геометрия в историческом развитии».
Материал, относящийся к линии «Наглядная геометрия» (элементы наглядной стереометрии) способствует развитию пространственных представлений учащихся в рамках изучения планиметрии.
Содержание разделов «Геометрические фигуры» и «Измерение геометрических величин» нацелено на получение конкретных знаний о геометрической фигуре как важнейшей математической модели для описания окружающего мира. Систематическое изучение свойств геометрических фигур позволит развить логическое мышление и показать применение этих свойств при решении задач вычислительного и конструктивного характера, а также практических.
Особенностью линии «Логика и множества» является то, что представленный здесь материал преимущественно изучается при рассмотрении различных вопросов курса. Соответствующий материал нацелен на математическое развитие учащихся, формирование у них умения точно, сжато и ясно излагать мысли в устной и письменной речи.
Линия «Геометрия в историческом развитии» предназначена для формирования представлений о геометрии как части человеческой культуры, для общего развития школьников, для создания культурно-исторической среды обучения.
Виды и формы проверки качества знаний предмета.
Контрольная работа проводится с целью определения конечного результата в обучении, умения применять знания для решения задач определенного типа, изучаемых в данной теме.
Проводятся следующие виды проверки знаний учащихся: стартовая, промежуточная, итоговая. Формы контроля: выполнение тестовых заданий в форме контрольной работы.
4.Описание места курса в учебном плане
На изучение геометрии в школе отводится 2 учебных часа в неделю, 68 учебных часов в год.
Контрольных работ - 8, в том числе стартовая, промежуточная и итоговая.
5.Личностные, метапредметные и предметные результаты освоения содержания курса
Программа обеспечивает достижение следующих результатов:
личностные:
-
формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учетом устойчивых познавательных интересов;
-
формирование целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
-
формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности;
-
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
-
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
-
креативность мышления, инициатива, находчивость, активность при решении геометрических задач;
-
умение контролировать процесс и результат учебной математической деятельности;
-
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
метапредметные:
-
умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
-
умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы;
-
умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
-
осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовых связей;
-
умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;
-
умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
-
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способу работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; слушать партнера; формулировать, аргументировать и отстаивать свое мнение;
-
формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
-
первоначальные представления об идеях и о методах математики как универсальном языке науки и техники, о средстве моделирования явлений и процессов;
-
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
-
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
-
умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
-
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
-
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
-
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
-
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
-
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
предметные:
-
овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (число, геометрическая фигура) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
-
умение работать с геометрическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
-
овладение навыками устных, письменных, инструментальных вычислений;
-
овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
-
усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне - о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;
-
умение измерять длины отрезков, величины углов, использовать формулы для нахождения периметров геометрических фигур (треугольника);
-
умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использование при необходимости справочных материалов, калькулятора, компьютера.
6.Содержание учебного предмета, курса
Наглядная геометрия (10 часов).
Наглядные представления о пространственных фигурах: куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр.
Геометрические фигуры (17 часов).
Прямые и углы. Точка, прямая, плоскость. Отрезок, луч. Угол. Виды углов. Вертикальные и смежные углы. Биссектриса угла.
Параллельные и пересекающиеся прямые. Перпендикулярные прямые. Теоремы о параллельности и перпендикулярности прямых. Перпендикуляр и наклонная к прямой. Серединный перпендикуляр к отрезку.
Геометрическое место точек. Свойства биссектрисы угла и серединного перпендикуляра к отрезку.
Треугольник. Высота, медиана, биссектриса, средняя линия треугольника. Равнобедренные и равносторонние треугольники; свойства и признаки равнобедренного треугольника. Признаки равенства треугольников. Неравенство треугольника. Соотношения между сторонами и углами треугольника.
Сумма углов треугольника. Внешние углы треугольника.
Окружность и круг. Дуга, хорда.
Построения с помощью циркуля и линейки. Основные задачи на построение: деление отрезка пополам; построение угла, равного данному; построение треугольника по трем сторонам; построение перпендикуляра к прямой; построение биссектрисы угла.
Решение задач на вычисление, доказательство и построение с использованием свойств изученных фигур (треугольника).
Измерение геометрических величин (13 часов).
Длина отрезка. Расстояние от точки до прямой. Расстояние между параллельными прямыми.
Периметр треугольника.
Градусная мера угла.
Решение задач на вычисление и доказательство с использование изученных формул.
Теоретико-множественные понятия (18 часов).
Множество, элемент множества. Задание множеств перечислением элементов, характеристическим свойством. Подмножество. Объединение и пересечение множеств.
Элементы логики (8 часов).
Определение. Аксиомы и теоремы. Доказательство. Доказательство от противного. Теорема, обратная данной. Пример и контрпример.
Понятие о равносильности, следовании, употребление логических связок если…, то…, в том и только в том случае, логические связки и, или.
Геометрия в историческом развитии (2 часа).
От землемерия к геометрии. Трисекция угла. «Начала» Евклида. Н.И. Лобачевский. История пятого постулата.
7.Тематическое планирование с определением основных видов учебной деятельности
№ п/п
Тема
Всего часов
Контрольные работы
Основные виды учебной деятельности
1.
Начальные геометрические сведения
10
1
Стартовая
Приводить примеры геометрических фигур.
Описывать точку, прямую, отрезок, луч, угол.
Формулировать:
определения: равных отрезков, середины отрезка, расстояния между двумя точками, дополнительных лучей, развёрнутого угла, равных углов, биссектрисы угла, смежных и вертикальных углов, пересекающихся прямых, перпендикулярных прямых, перпендикуляра, наклонной, расстояния от точки до прямой;
свойства: расположения точек на прямой, измерения отрезков и углов, смежных и вертикальных углов, перпендикулярных прямых; основное свойство прямой.
Классифицировать углы.
Доказывать: теоремы о пересекающихся прямых, о свойствах смежных и вертикальных углов, о единственности прямой, перпендикулярной данной (случай, когда точка лежит на данной прямой).
Находить длину отрезка, градусную меру угла, используя свойства их измерений.
Изображать с помощью чертёжных инструментов геометрические фигуры: отрезок, луч, угол, смежные и вертикальные углы, перпендикулярные прямые, отрезки и лучи.
Пояснять, что такое аксиома, определение.
Решать задачи на вычисление и доказательство, проводя необходимые доказательные рассуждения
2.
Треугольники
17
1
Описывать смысл понятия «равные фигуры». Приводить примеры равных фигур.
Изображать и находить на рисунках равносторонние, равнобедренные, прямоугольные, остроугольные, тупоугольные треугольники и их элементы.
Классифицировать треугольники по сторонам и углам.
Формулировать:
определения: остроугольного, тупоугольного, прямоугольного, равнобедренного, равностороннего, разностороннего треугольников; биссектрисы, высоты, медианы треугольника; равных треугольников; серединного перпендикуляра отрезка; периметра треугольника;
свойства: равнобедренного треугольника, серединного перпендикуляра отрезка, основного свойства равенства треугольников;
признаки: равенства треугольников, равнобедренного треугольника.
Доказывать теоремы: о единственности прямой, перпендикулярной данной (случай, когда точка лежит вне данной прямой); три признака равенства треугольников; признаки равнобедренного треугольника; теоремы о свойствах серединного перпендикуляра, равнобедренного и равностороннего треугольников.
Разъяснять, что такое теорема, описывать структуру теоремы. Объяснять, какую теорему называют обратной данной, в чём заключается метод доказательства от противного. Приводить примеры использования этого метода.
Решать задачи на вычисление и доказательство
3.
Параллельные прямые
13
1
Промежуточная
Распознавать на чертежах параллельные прямые.
Изображать с помощью линейки и угольника параллельные прямые.
Описывать углы, образованные при пересечении двух прямых секущей.
Формулировать:
определения: параллельных прямых, расстояния между параллельными прямыми, внешнего угла треугольника, гипотенузы и катета;
свойства: параллельных прямых; углов, образованных при пересечении параллельных прямых секущей; суммы улов треугольника; внешнего угла треугольника; соотношений между сторонами и углами треугольника; прямоугольного треугольника; основное свойство параллельных прямых;
признаки: параллельности прямых, равенства прямоугольных треугольников.
Доказывать: теоремы о свойствах параллельных прямых, о сумме углов треугольника, о внешнем угле треугольника, неравенство треугольника, теоремы о сравнении сторон и углов треугольника, теоремы о свойствах прямоугольного треугольника, признаки параллельных прямых, равенства прямоугольных треугольников.
Решать задачи на вычисление и доказательство
4.
Соотношения между сторонами и углами треугольника
18
2
Пояснять, что такое задача на построение; геометрическое место точек (ГМТ). Приводить примеры ГМТ.
Изображать на рисунках окружность и её элементы; касательную к окружности; окружность, вписанную в треугольник, и окружность, описанную около него. Описывать взаимное расположение окружности и прямой.
Формулировать:
определения: окружности, круга, их элементов; касательной к окружности; окружности, описанной около треугольника, и окружности, вписанной в треугольник;
свойства: серединного перпендикуляра как ГМТ; биссектрисы угла как ГМТ; касательной к окружности; диаметра и хорды; точки пересечения серединных перпендикуляров сторон треугольника; точки пересечения биссектрис углов треугольника;
признаки касательной.
Доказывать: теоремы о серединном перпендикуляре и биссектрисе угла; о свойствах касательной; об окружности, вписанной в треугольник, описанной около треугольника; признаки касательной.
Решать основные задачи на построение: построение угла, равного данному; построение серединного перпендикуляра данного отрезка; построение прямой, проходящей через данную точку и перпендикулярной данной прямой; построение биссектрисы данного угла; построение треугольника по двум сторонам и углу между ними; по стороне и двум прилежащим к ней углам.
Решать задачи на построение.
Строить треугольник по трём сторонам.
Решать задачи на вычисление, доказательство и построение
5.
Повторение. Решение задач
8
Итоговая
6.
Резерв
2
Итого:
68
8
Календарно - тематическое планирование.1
Система оценки достижения планируемых результатов2.
Оценивание знаний обучающихся3.
8.Описание учебно - методического и материально - технического обеспечения образовательного процесса
Нормативные документы
1. Федеральный государственный стандарт общего среднего образования.
2. Примерные программы по учебным предметам. Математика. 5-9 классы.
3. Бутузов В.Ф. Геометрия. Рабочая программа к учебнику Л.С. Атанасяна и других. 7-9 классы: пособие для учителей общеобразов. учреждений / В.Ф.Бутузов. - М.: Просвещение, 2011. - 31 с.
Учебная литература основная
Геометрия: 7 - 9. Учебник для общеобразовательных учреждений. / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г.Позняк, И.И. Юдина.- М.: Просвещение, 2013 - 384 с.: ил.
Дидактические материалы, рабочие тетради
Геометрия: рабочая тетрадь: 7 кл. /Л.С.Атанасян, В.Ф.Бутузов, Ю.А.Глазков, И.И.Юдина. - М.: Просвещение, 2011.
Интернет-ресурсы
1. ilib.mirrorl.mccme.ru/
2. window.edu.ru/window/library/
3. www.problems.ru/
4. kvant.mirrorl.mccme.ru/
5. www.etudes.ru/
9.Планируемые результаты изучения
курса геометрии в 7 классе
Наглядная геометрия
Учащийся научится:
-
распознавать на чертежах, рисунках, моделях и в окружающем мире плоские и пространственные геометрические фигуры (точка, прямая, отрезок, луч, угол, треугольник, окружность, шар, сфера, параллелепипед, пирамида и др.).
Геометрические фигуры
Учащийся научится:
-
пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения;
-
распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации;
-
находить значения длин линейных элементов фигур и их отношения, градусную меру углов от 0 до 180ͦ
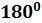
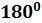 ,
применяя определения, свойства и признаки фигур и их элементов,
отношения фигур (равенство);
,
применяя определения, свойства и признаки фигур и их элементов,
отношения фигур (равенство);
-
решать задачи на доказательство, опираясь на изученные свойства фигур и отношений между ними и применяя изученные методы доказательств;
-
решать несложные задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки;
-
решать простейшие планиметрические задачи в пространстве.
Измерение геометрических величин
Учащийся научится:
-
использовать свойства измерения длин и углов при решении задач на нахождение длины отрезка и градусной меры угла;
-
вычислять длины линейных элементов треугольников и их углы;
-
вычислять периметры треугольников;
-
решать практические задачи, связанные с нахождением геометрических величин (используя при необходимости справочники и технические средства).
Начальные геометрические сведения.
научится:
- пользоваться языком геометрии для описания предметов окружающего мира и их конфигурации;
- распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации;
- использовать свойства измерения длин и углов при решении задач на нахождение длин отрезков и градусной меры угла;
- находить градусную меру углов, применяя определения и свойства смежных и вертикальных углов.
Треугольники.
научится:
- пользоваться языком геометрии для описания предметов окружающего мира и их конфигурации;
- распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации;
- находить значения длин линейных элементов фигур, градусную меру углов от 0º до 180º, применяя определения, свойства и признаки фигур и их элементов;
- решать задачи на доказательство, опираясь на изученные свойства фигур и применяя изученные методы доказательства;
- решать несложные задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки.
Параллельные прямые.
научится:
- пользоваться языком геометрии для описания предметов окружающего мира и их конфигурации;
- распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации;
- находить градусную меру углов от 0º до 180º, применяя определения, свойства и признаки фигур и их элементов;
- решать задачи на доказательство, опираясь на изученные свойства фигур и применяя изученные методы доказательства.
Соотношения между сторонами и углами треугольника.
научится:
- пользоваться языком геометрии для описания предметов окружающего мира и их конфигурации;
- распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации;
- находить градусную меру углов от 0º до 180º, применяя определения, свойства и признаки фигур и их элементов;
- решать задачи на доказательство, опираясь на изученные свойства фигур и применяя изученные методы доказательства;
- решать несложные задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки.
ПРИЛОЖЕНИЕ
к рабочей программе по предмету «Геометрия»
Система оценки достижения планируемых результатов
освоения программы
Стартовая контрольная работа (20 минут)
Вариант 1
1. Найти площадь прямоугольника, если длина его на 2,5 см больше ширины, а периметр его равен 19 см.
2. На координатной плоскости отметьте точки М(4;0), N(0;5),К(2;-5). Укажите координаты точки пересечения отрезка КN с осью ОХ.
Вариант 2
1. Найти площадь прямоугольника, если его ширина на 3,5 см меньше длины, а периметр равен 23.
2. На координатной плоскости отметьте точки А(0;8), В(-3;0),С(3;2). Укажите координаты точки пересечения отрезка ВС с осью ОУ.
Промежуточная контрольная работа (25 минут)
-
вариант
2.
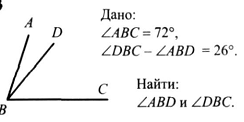
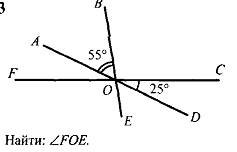
-
вариант
2.
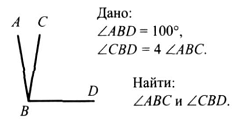
3.
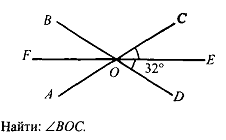


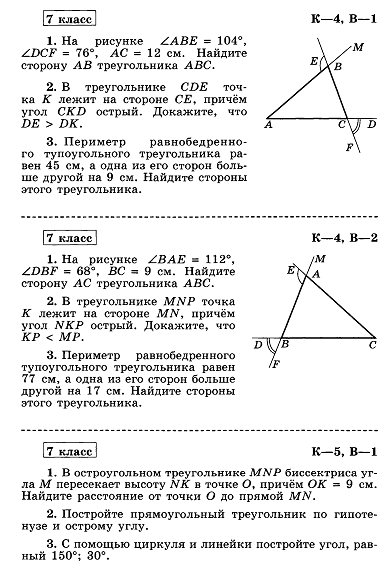

Итоговая контрольная работа по геометрии
Учени_____ 7 класса
Ф.И. __________________________________________
Вариант 1
1. Один из смежных углов равен 400 . Сколько градусов другой угол?
Ответ:________
2. Выберите правильное утверждение:
1. Две прямые параллельны, если накрест лежащие углы равны.
2. Две прямые параллельны, если вертикальные углы равны.
3. Две прямые параллельны, если односторонние углы равны.
4. Две прямые параллельны, если сумма соответственных углов равна 1800.
3. Два угла треугольника равны 1070 и 230. Сколько градусов третий угол этого треугольника?
Ответ:__________
4. В равнобедренном треугольнике угол при основании равен 700 .Чему равны остальные углы?
1. 700 и 700 2. 550 и 550 3. 700 и 400 4. невозможно вычислить
5. Треугольник АВС - равнобедренный (АВ=ВС). ВД-высота. ВД=4 м, АС= 6 м, АВ=5 м. Чему равны стороны треугольника ВДС.
В
А С
Д
1. 5м, 4м и 4м 2. 3м, 5м и 4м. 3. 5м, 4м и 5м 4. невозможно вычислить.
6. d в По чертежу найдите угол 1, если
1230 известно, что в с.
с Перечертите, запишите дано, найти,
-
решение.
7. Найдите углы треугольника АВС ,если угол А на 60 ° меньше угла В и в 2 раза меньше угла С.
Итоговая контрольная работа по геометрии
Учени_____ 7 класса
Ф.И. __________________________________________
Вариант 2
1. Два угла треугольника равны 1160 и 340. Сколько градусов третий угол этого треугольника?
Ответ:___________
2. Выберите правильное утверждение:
1. Если односторонние углы равны, то две прямые параллельны
2. Если соответственные углы равны, то две прямые параллельны
3. Если сумма соответственных углов равна 1800, то две прямые параллельны.
4. Если сумма накрест лежащих углов равна 1800, то две прямые параллельны.
3. Один из вертикальных углов равен 400. Сколько градусов другой угол?
Ответ:_________
4. В равнобедренном треугольнике угол при вершине равен 700 .Чему равны остальные углы?
1. 700 и 700 2. 550 и 550 3. 700 и 400 4. невозможно вычислить
В
5. Треугольник АВС - равнобедренный (АВ=ВС). ВД-медиана.
Угол АВД= 400. Чему равны углы треугольника ВДС.
А С
Д
-
400 900 и 500 2. 450, 450 и 900 3. 400, 400 и 1000 4. невозможно вычислить
6. с По чертежу найдите угол 1, если
1 а известно, что а в.
Перечертите, запишите дано, найти,
в решение.
460
7. Периметр равнобедренного треугольника равен 48 см. Его боковая сторона в 1,5 раза больше основания. Вычислите стороны треугольника.
1 См. Приложение «Календарно - тематическое планирование уроков»
2 См. Приложение «Система оценки достижения планируемых результатов освоения программы»
3</<sup> См. локальный акт школы «Положение об оценивании знаний обучающихся»