Рабочая программа по геометрии 11 класс Атанасян

Пояснительная записка

к рабочей программе по геометрии в 11 классе

Рабочая программа по математике составлена на основе федерального компонента государственного стандарта основного общего образования. Рабочая программа составлена на основе авторской программы Л.С. Атанасяна и др. по геометрии (М.: Просвещение, 2010).

Выбор данной программы мотивирован тем, что она разработана в соответствии с требованиями федерального компонента государственного стандарта среднего (полного) общего образования по математике (базовый уровень обучения), обеспечена учебно-методическим комплектом по геометрии для 10-11 классов (авторы Л.С. Атанасян и др. (М.: Просвещение)), рекомендована Министерством образования РФ для общеобразовательных классов.

В программе определена последовательность изучения материала в рамках стандарта для старшей школы и пути формирования знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования, а так же развития учащихся.

Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса.

Рабочая программа выполняет две основные функции:

Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.

Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.

Примерная программа конкретизирует содержание предметных тем образовательного стандарта и даёт примерное распределение учебных часов по разделам курса.

Для продуктивной деятельности в современном мире требуется достаточно прочная математическая подготовка. Геометрия - один из важнейших компонентов математического образования. Она необходима для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, развития пространственного воображения и интуиции, математической культуры и эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления и формирование понятия доказательства.

Значимость математической подготовки в общем образовании современного человека повлияла на определение целей изучения математики на ступени среднего (полного) общего образования.

Цели

Изучение математики на базовом уровне среднего (полного) общего образования направлено на достижение следующих целей:

• формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;

• развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;

• овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;

• воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры

Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и показывает распределение учебных часов по разделам курса. Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение геометрии в 11 (базовый уровень) классе отводится 68 часов из расчёта 2 часа в неделю. Рабочая программа по геометрии для 11 класса рассчитана на это же количество часов.

Задачи курса геометрии для достижения поставленных целей:

1. изучение свойств пространственных тел;

2. формирование умений применять полученные знания для решения практических задач, проводить доказательные рассуждения, логически обосновывать выводы для изучения школьных естественнонаучных дисциплин на базовом уровне.

Основной формой организации образовательного процесса в 11 классе является урок. Формы организации учебного процесса на уроке: индивидуальные, групповые, фронтальные. Технические средства обучения: ноутбук, мультимедиапроектор.

Контроль уровня усвоения содержания образования является неотъемлемой составной частью процесса обучения. Промежуточная аттестация обучающихся в узком смысле осуществляется в 11 классе через устный и письменный опросы (индивидуальная работа по карточкам), самостоятельные и контрольные работы по разделам учебного материала, тестирование.

Результаты обучения по курсу «Геометрия»

Результаты обучения представлены в Требованиях к уровню подготовки выпускников и задают систему итоговых результатов обучения, которых должны достигать все школьники, изучавшие геометрию на базовом уровне, и достижение которых является обязательным условием положительной аттестации за курс средней школы.

Реализация рабочей программы осуществляется на основе использования учебника: Геометрия. 10-11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. - М.: Просвещение, 2011.

Учебник полностью соответствует требованиям федерального компонента государственного стандарта общего образования по математике базового уровня (обязательному минимуму содержания образования и требованиям к математической подготовке учащихся). Книга написана в соответствии с действующей программой для общеобразовательной школы, имеет гриф «Рекомендовано» Министерства образования и науки РФ и входит в Федеральный комплект учебников.

Учебник дает цельное и полное представление о школьном курсе стереометрии, который базируется на сочетании наглядности и логической строгости. Теоретический материал в учебнике изложен доступно для большинства обучающихся. Это способствует решению важной педагогической задачи - научить работать с книгой.

Важная роль при изучении стереометрии отводится задачам. Учебник содержит большое количество разнообразных по трудности задач, что дает возможность осуществлять индивидуальный подход к обучающимся.

Учитывая изменения в содержательной части ЕГЭ (4 геометрические задачи в 1 части и 2 задачи - во 2 части), решение при изучении курса большого количества задач поможет старшеклассникам лучше подготовиться к ЕГЭ.

СОДЕРЖАНИе материала

1. Координаты точки и координаты векторов пространстве. Движения (17 ч).

Прямоугольная система координат в пространстве. Расстояние между точками в пространстве. Векторы в пространстве. Длина вектора. Равенство векторов. Сложение векторов. Умножение вектора на число. Координаты вектора. Скалярное произведение векторов.

Цель: введение понятие прямоугольной системы координат в пространстве; знакомство с координатно-векторным методом решения задач.

Цели: сформировать у учащихся умения применять координатный и векторный методы к решению задач на нахождение длин отрезков и углов между прямыми и векторами в пространстве. В ходе изучения темы целесообразно использовать аналогию между рассматриваемыми понятиями на плоскости и в пространстве. Это поможет учащимся более глубоко и осознанно усвоить изучаемый материал, уяснить содержание и место векторного и координатного методов в курсе геометрии

О с н о в н а я ц е л ь - обобщить и систематизировать представления учащихся о декартовых координатах и векторах, познакомить с полярными и сферическими координатами.

Изучение координат и векторов в пространстве, с одной стороны, во многом повторяет изучение соответствующих тем планиметрии, а с другой стороны, дает алгебраический метод решения стереометрических задач.

1. Цилиндр, конус, шар (15 ч)

Основные элементы сферы и шара. Взаимное расположение сферы и плоскости. Многогранники, вписанные в сферу. Многогранники, описанные около сферы. Цилиндр и конус. Фигуры вращения.

Цель: выработка у учащихся систематических сведений об основных видах тел вращения.

Цели: дать учащимся систематические сведения об основных видах тел вращения. Изучение круглых тел (цилиндра, конуса, шара) завершает изучение системы основных пространственных геометрических тел. В ходе знакомства с теоретическим материалом темы значительно развиваются пространственные представления учащихся: круглые тела рассматривать на примере конкретных геометрических тел, изучать взаимное расположение круглых тел и плоскостей (касательные и секущие плоскости), ознакомить с понятиями описанных и вписанных призм и пирамид. Решать большое количество задач, что позволяет продолжить работу по формированию логических и графических умений.

О с н о в н а я ц е л ь - сформировать представления учащихся о круглых телах, изучить случаи их взаимного расположения, научить изображать вписанные и описанные фигуры.

В данной теме обобщаются сведения из планиметрии об окружности и круге, о взаимном расположении прямой и окружности, о вписанных и описанных окружностях. Здесь учащиеся знакомятся с основными фигурами вращения, выясняют их свойства, учатся их изображать и решать задачи на фигуры вращения. Формированию более глубоких представлений учащихся могут служить задачи на комбинации многогранников и фигур вращения.

2. Объем и площадь поверхности (26 ч).

Понятие объема и его свойства. Объем цилиндра, прямоугольного параллелепипеда и призмы. Принцип Кавальери. Объем пирамиды. Объем конуса и усеченного конуса. Объем шара и его частей. Площадь поверхности многогранника, цилиндра, конуса, усеченного конуса. Площадь поверхности шара и его частей.

Цель: систематизация изучения многогранников и тел вращения в ходе решения задач на вычисление их объемов.

Цели: продолжить систематическое изучение многогранников и тел вращения в ходе решения задач на вычисление их объемов.

Понятие объема вводить по аналогии с понятием площади плоской фигуры и формулировать основные свойства объемов.

Существование и единственность объема тела в школьном курсе математики приходится принимать без доказательства,

так как вопрос об объемах принадлежит, по существу, к трудным разделам высшей математики. Поэтому нужные результаты устанавливать, руководствуясь больше наглядными соображениями. Учебный материал главы в основном должен усвоиться в процессе решения задач.

О с н о в н а я ц е л ь - сформировать представления учащихся о понятиях объема и площади поверхности, вывести формулы объемов и площадей поверхностей основных пространственных фигур, научить решать задачи на нахождение объемов и площадей поверхностей.

Изучение объемов обобщает и систематизирует материал планиметрии о площадях плоских фигур. При выводе формул объемов используется принцип Кавальери. Это позволяет чисто геометрическими методами, без использования интеграла или предельного перехода, найти объемы основных пространственных фигур, включая объем шара и его частей.

Практическая направленность этой темы определяется большим количеством разнообразных задач на вычисление объемов и площадей поверхностей.

3. Повторение (10 ч.)

Цель: повторение и систематизация материала 11 класса.

Цели: повторить и обобщить знания и умения, учащихся через решение задач по следующим темам: метод координат в пространстве; многогранники; тела вращения; объёмы многогранников и тел вращения

ТРЕБОВАНИЯ К УРОВНЮ

ПОДГОТОВКИ ВЫПУСКНИКОВ

В результате изучения математики на базовом уровне ученик должен

знать/понимать¹

• значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;

• значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;

• универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;

Геометрия

уметь

• распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;

• описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;

• анализировать в простейших случаях взаимное расположение объектов в пространстве;

• изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;

• строить простейшие сечения куба, призмы, пирамиды;

• решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);

• использовать при решении стереометрических задач планиметрические факты и методы;

• проводить доказательные рассуждения в ходе решения задач;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;

• вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.

• вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.

Календарно-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

МАТЕРИАЛА по геометрии в 11 классе

Контрольная работа № 1

Вариант 1

1. Найдите координаты вектора , если А (5; -1; 3), В (2; -2; 4).

2. Даны векторы (3; 1; -2) и (1; 4; -3). Найдите .

3. Изобразите систему координат Oxyz и постройте точку А (1; -2; -4). Найдите расстояния от этой точки до координатных плоскостей.

Вариант 2

1. Найдите координаты вектора , если С (6; 3; - 2), D (2; 4; - 5).

2. Даны вектора (5; - 1; 2) и (3; 2; - 4). Найдите .

3. Изобразите систему координат Oxyz и постройте точку В (- 2; - 3; 4). Найдите расстояние от этой точки до координатных плоскостей.

Контрольная работа № 2

Вариант 1

1. Вычислите скалярное произведение векторов и , если , , = 2, = 3, = 60°, , .

2. Дан куб ABCDA₁B₁C₁D₁. Найдите угол между прямыми AD₁ и BM, где M - середина ребра DD₁.

3. При движении прямая отображается на прямую b₁, а плоскость β - на плоскость β₁ и b || β₁.

Вариант 2

1. Вычислите скалярное произведение векторов и , если , , = 3, = 2, = 60°, , .

2. Дан куб ABCDA₁B₁C₁D₁. Найдите угол между прямыми AC и DC₁.

3. При движении прямая a отображается на прямую a₁, плоскость α - на плоскость α₁, и . Докажите, что .

Контрольная работа № 3

Вариант 1

1. Осевое сечение цилиндра - квадрат, площадь основания цилиндра равна 16π см². Найдите площадь поверхности цилиндра.

2. Высота конуса равна 6 см, угол при вершине осевого сечения равен 120°. Найдите:

а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 30°;

б) площадь боковой поверхности конуса.

3. Диаметр шара равен 2m. Через конец диаметра проведена плоскость под углом 45° к нему. Найдите длину линии пересечения сферы с этой плоскостью.

Вариант 2

1. Осевое сечение цилиндра - квадрат, диагональ которого 4 см. Найдите площадь поверхности цилиндра.

2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30°. Найдите:

а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60°;

б) площадь боковой поверхности конуса.

3. Диаметр шара равен 4m. Через конец диаметра проведена плоскость под углом 30° к нему. Найдите площадь сечения шара этой плоскостью.

Контрольная работа № 4

Вариант 1

1. Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен 60°. Найдите объем пирамиды.

2. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2a, а прилежащий угол равен 30°. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45°. Найдите объем цилиндра.

Вариант 2

1. Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол в 60°. Найдите объем пирамиды.

2. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2a, а прилежащий угол равен 30°. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол в 45°. Найдите объем конуса.

Контрольная работа № 5

Вариант 1

1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 60°. Найдите отношение объемов конуса и шара.

2. Объем цилиндра равен 96π см³, площадь его осевого сечения 48 см². Найдите площадь сферы, описанной около цилиндра.

Вариант 2

1. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.

2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов цилиндра и шара.

Тесты по планиметрии

Вариант I

(все длины указаны в см)

Прямоугольные треугольники ABC и A′B′C′ подобны. Если A =

= 35°, то треугольник A′B′C′ имеет угол, равный

1) 45° 2) 65° 3) 145° 4) 55°

В треугольниках ABC и A′B′C′ B =B′, BC = 6, B′C′ = 4. Если 2 AB = 3A′B′, то отношение A′C′ равно

1) 2) 2 3) 4)

Вписанный угол опирается на дугу 84°. Градусная мера угла равна

1) 84° 2) 174° 3) 168° 4) 42°На дугу AB опирается вписанный угол, содержащий 20°. Если вписанный угол ADC равен α, то

1) α = 20° 2) α > 20° 3) α < 20°

4) α зависит от положения точки D на дуге FB

Сумма внутренних углов выпуклого пятиугольника равна

1) 540° 2) 900° 3) 720° 4) 480°

Если внешний угол правильного многоугольника содержит 60°, то число его сторон равно

1) 6 2) 5 3) 4 4) 8В окружность радиуса 5 вписан прямоугольник, одна из сторон которого равна 6. Найдите непараллельную ей сторону.

1) 4 2) 5 3) 6 4) 8

Укажите ложное утверждение.

1) Любые два квадрата подобны.

2) Любые два угла подобны.

3) Любые две окружности подобны.

4) Любые два правильных пятиугольника подобны.

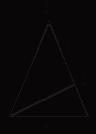
В треугольнике ABC A = 60°, AB = 3, AC = 2. Найдите BC.

1) 7 2) 3) 4) 19

В треугольнике ABC sin C =, sin A =, BC = 8. Найдите AB.

1) 3 2) 4 3) 6 4) 2ABCDEFHG - правильный восьмиугольник. Найдите BGD.

1) 75° 2) 30° 3) 45° 4) 60°

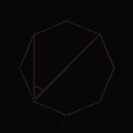
В треугольнике ABC B =D = 90°,

BD = 3, AD = 2. Найдите DC.

1) 4,5 2) 6 3) 5 4) 1,5

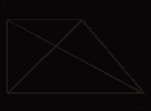
Р9МГ - 3137

(все длины указаны в см)В трапеции ABCD AD || BC, BO = 3, OD = 6. Если OC = 2, то диагональ AC равна

1) 4 2) β 3) 9 4) 11

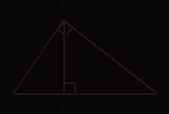
Около треугольника ABC описана окружность с центром в точке O. Если A = 20°, B = 70°, то

1) точка O лежит внутри треугольника.

2) о положении точки O ничего сказать нельзя.

3) точка O лежит вне треугольника.

4) точка O лежит на одной из сторон треугольника.В треугольнике ABC BD AC,

A = 30°. Если DBC = 45°, AB = 4, то сторона BC равна

1) 2 2) 3) 2 4) 3

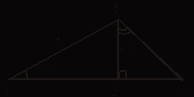
Радиус описанной около правильного многоугольника окружности равен 6. Если радиус вписанной окружности 3, то сторона многоугольника равна

1) 3 2) 6 3) 6 4) 6

Сторона ромба равна 3. Если одна из диагоналей равна 4, то косинус тупого угла ромба

1) 2) 3) 4) В треугольнике ABC AD - биссектриса угла A, AB = BC. Если AC = 6, BD = 8, то сторона AB равна

1) 11 2) 14 3) 12 4) 10

Вариант II

Р9МГ - 4139

(все длины указаны в см)

Прямоугольные треугольники ABC и A′B′C′ подобны. Если A′ =

= 42°, то треугольник ABC имеет угол, равный

1) 84° 2) 58° 3) 48° 4) 36°

В треугольниках ABC A′B′C′ B =B′, B′C′ = 12, BC = 3. Если A′B′ = 4AB, то отношение A′C′ : AC равно

1) 3 2) 4 3) 4)

Вписанный угол опирается на дугу 76°. Градусная мера угла равна

1) 176° 2) 104° 3) 38° 4) 152°На дугу AB опирается вписанный угол, содержащий 70°. Если вписанный угол ADC равен α, то

1) α = 70° 2) α > 70° 3) α < 70°

4) α зависит от положения точки D на дуге FB

Сумма внутренних углов выпуклого семиугольника равна

1) 900° 2) 720° 3) 360° 4) 540°

Если внешний угол правильного многоугольника содержит 30°, то число сторон многоугольника равно

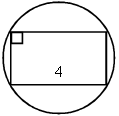
1) 9 2) 10 3) 8 4) 12В окружность радиуса 2,5 вписан прямоугольник, одна из сторон которого равна 4. Найдите непараллельную ей сторону.

1) 2 2) 3,5 3) 2,5 4) 3

Укажите верное утверждение.

1) Любые две окружности подобны.

2) Любые два угла подобны.

3) Любые два треугольника подобны.

4) Любые две трапеции подобны.

В треугольнике ABC C = 150°, AC =, BC = 2. Найдите AB.

1) 2 2) 1 3) 4)

В треугольнике ABC AC = 4, sin C =, sin B =. Найдите AB.

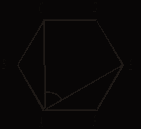
1) 4 2) 3 3) 12 4) 6ABCDEF - правильный шестиугольник. Найдите CAE.

1) 30° 2) 60° 3) 75° 4) 90°

В треугольнике ABC B =D = 90°, BD = 2, DC = 4. Найдите AD.

1) 1 2) 2 3) 2 4)

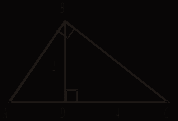
В трапеции ABCD AD || BC, DO = 15, BO = 5. Если OC = 3, то диагональ AC равна

1) 9 2) 12 3) 25 4) 28

Около треугольника ABC описана окружность с центром в точке O. Если B = 45°, C = 15°, то

1) точка O лежит на одной из сторон треугольника

2) точка O лежит внутри треугольника

3) положение точки O определить нельзя

4) точка O лежит вне треугольникаВ треугольнике ABC BD AC. Если A = 60°, C = 45°, DC =, то сторона AB равна

1) 2 2) 3) 2 4) 2

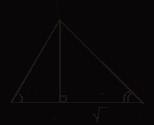
Радиус вписанной в правильный многоугольник окружности равен 2. Если радиус описанной окружности 4, то сторона многоугольника равна

1) 2 2) 4 3) 4 4) 6

Сторона ромба равна 3. Если одна из диагоналей равна 5, то косинус острого угла ромба равен

1) 2) 3) 4) В треугольнике ABC AD - биссектриса угла A, AB = BC. Если AC = 9, BD = 12, то сторона BC равна

1) 18 2) 15 3) 24 4) 21

Вариант III

(все длины указаны в см)

Прямоугольные треугольники ABC и A′B′C′ подобны. Если B =

= 28°, то треугольник A′B′C′ имеет угол, равный

1) 152° 2) 62° 3) 52° 4) 64°

В треугольниках ABC и A′B′C′ C =C′, AC = 4, A′C′ = 8. Если B′C′ = 2BC, то отношение AB : A′B′ равно

1) 2) 2 3) 4 4)

Вписанный угол содержит 130°. Градусная мера дуги, на которую он опирается, равна

1) 65° 2) 130° 3) 220° 4) 260°На дугу AB опирается вписанный угол, содержащий 30°. Если вписанный угол ADC равен β, то

1) β < 30° 2) β = 30° 3) β > 30°

4) β зависит от положения точки D на дуге AF

Сумма внутренних углов выпуклого многоугольника 1080°. Тогда число сторон многоугольника равно

1) 6 2) 7 3) 8 4) 9

Внешний угол правильного шестиугольника равен

1) 30° 2) 60° 3) 72° 4) 54°В окружность вписан прямоугольник со сторонами 8 и 6. Найдите радиус этой окружности.

1) 5 2) 6 3) 4 4) 10

Укажите ложное утверждение.

1) Любые две окружности подобны.

2) Любые два отрезка подобны.

3) Любые два квадрата подобны.

4) Любые два ромба подобны.

В треугольнике ABC A = 45°, AB = 2, AC = 1. Найдите BC.

1) 13 2) 3) 5 4)

В треугольнике ABC BC = 9, AB = 6, sin C =. Найдите sin A.

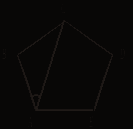
1) 2) 3) 4) ABCDE - правильный пятиугольник. Найдите BAC.

1) 15° 2) 18° 3) 36° 4) 30°

В треугольнике ABC C =D = 90°, AC = 6, AD = 4. Найдите гипотенузу AB.

1) 18 2) 13 3) 12 4) 9

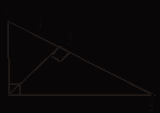
В трапеции ABCD AD || BC, AD = 6,

BC = 3. Если BO = 2, то диагональ BD равна

1) 4 2) 9 3) 5 4) 6

Около треугольника ABC описана окружность с центром в точке O. Если A = 65°, B = 35°, то

1) точка O лежит на одной из сторон треугольника.

2) точка O лежит вне треугольника.

3) точка O лежит внутри треугольника.

4) положение точки O определить нельзя.В треугольнике ABC BD AC, ABC =

= 105°. Если DBC = 60°, AD = 2, то отрезок DC

равен

1) 2 2) 2 3) 3 4) 3

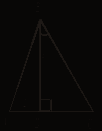
Сторона правильного многоугольника равна 8. Если радиус вписанной в него окружности 4, то радиус описанной окружности равен

1) 12 2) 6 3) 8 4) 8

Сторона ромба равна 3. Если одна из диагоналей равна 2, то косинус тупого угла ромба равен

1) 2) 3) 4) В треугольнике ABC BD - биссектриса угла B, ABD = α. Если AB = 6, AC =

= 12, DC = 8, то A равен

1) 2α 2) 90° - α 3) α

4) 90° - 2α

Вариант IV

На плоскости заданы прямоугольная система координат Oxy и координатные векторы и .

Разложение вектора {-4; 3} по координатным векторам и имеет вид

1) 2)

3) 4)

Вектор, равный сумме векторов и , имеет координаты

1) {1; 2} 2) {2; 1} 3) {3; 4} 4) {-1; 2}

Числа x и y, удовлетворяющие условию , равны1) x = -3

y = 0

2) x = 0

y = 3

3) x = 3

y = 0

4) x = 0

y = -3

Длина вектора {3; -2} равна

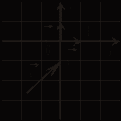
1) 2) 3) 5 4) 13Вектор , изображенный на чертеже, имеет координаты

1) {2; 1} 2) {0; -1} 3) {2; -1}

4) {-2; -1}

ABCD - параллелограмм. Если A (3; -4) и C (-3; -2), то координаты точки пересечения диагоналей равны

1) (0; -3) 2) (0; -1) 3) (3; -1) 4) (6; -2)

Пусть заданы точки A (-4; -3) и B (1; 2). Тогда вектор имеет координаты

1) {5; 5} 2) {-3; -1} 3) {-5; -5} 4) {3; 1}

Для решения задач 8 и 9 задана единичная полуокружность, изображенная на рис.

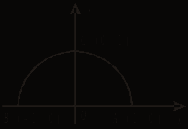
На единичной полуокружности лежит точка M . Косинус угла AOM равен

1) 2) 3) 4)

На единичной полуокружности лежит точка M . Площадь треугольника AOM равна

1) 0,8 2) 0,6 3) 0,3 4) 0,48

В треугольнике ABC C = 90°. Если AB = 4, AC = 2, то угол A равен

1) 30° 2) 60° 3) 75° 4) 45°

В треугольнике ABC AB = 5, BC = 7. Отношение (sin A) : (sin C) равно

1) 1 2) 3) 4)

В треугольнике ABC AC = 2, BC = 3. Если cos C =, то сторона AB равна

1) 4 2) 3 3) 4)

Уравнение прямой, проходящей через точку A (-8; 7) и параллельной оси Oy, имеет вид

1) x + y + 1 = 0 2) y - 7 = 0 3) y + 7 = 0 4) x + 8 = 0

Уравнение окружности с центром в точке (1; -3), проходящей через точку (1; -1), имеет вид

1) (x + 1)² + (y - 3)² = 4 2) (x - 1)² + (y + 3)² = 4

3) (x + 1)² + (y - 3)² = 2 4) (x - 1)² + (y + 3)² = 2Точки B (1; 0), C (2; -3), D (1; -1) - вершины параллелограмма ABCD. Координаты вершины A равны

1) (-2; 4) 2) (0; 2) 3) (2; -4) 4) (2; -2)

В треугольнике ABC A = α, B = β. Если BC = 2, AB = 3, C = 45°, то

1) α < 45° < 90° < β 2) α < 45° < β < 90°

3) 45 ° < α < β < 90° 4) α < β < 45°

Расстояние между двумя точками A и B равно 5. Если A (-2; 3) и B (1; y), то

1) B (1; 7) 2) такой точки B не существует

3) B (1; 7) или B (1; -1) 4) B (1; -5) или B (1; -1)

Даны точки A (0; -1), B (-1; 0), C (-1; 2). Если , то координаты точки K равны

1) (-1; 2) 2) (1; 2) 3) (1; 0) 4) (1; -4)

Итоговая контрольная работа по стереометрии

Вариант I

В правильной четырехугольной пирамиде MABCD сторона основания равна 6, а боковое ребро - 5. Найдите:

1) площадь боковой поверхности пирамиды;

2) объем пирамиды;

3) угол наклона боковой грани к плоскости основания;

4) скалярное произведение векторов (AD + AB) ∙ AM;

5) площадь описанной около пирамиды сферы;

6) угол между BD и плоскостью DMC.

Вариант II

В правильной треугольной пирамиде MABC сторона основания равна 3, а боковое ребро - 5. Найдите:

1) площадь боковой поверхности пирамиды;

2) объем пирамиды;

3) угол между боковым ребром и плоскостью основания;

4) скалярное произведение векторов , где E - середина BC;

5) объем вписанного в пирамиду шара;

6) угол между стороной основания и плоскостью боковой грани.

Вариант III

В правильной четырехугольной пирамиде MABCD боковое ребро равно 8 и наклонено к плоскости основания под углом 60°. Найдите:

1) площадь боковой поверхности пирамиды;

2) объем пирамиды;

3) угол между противоположными боковыми гранями;

4) скалярное произведение векторов , где E - середина DC;

5) объем описанного около пирамиды шара;

6) угол между боковым ребром AM и плоскостью DMC.

Вариант IV

В правильной треугольной пирамиде MABC сторона основания равна 2, а боковые грани наклонены к основанию под углом 60°.

Найдите:

1) площадь боковой поверхности пирамиды;

2) объем пирамиды;

3) угол между боковым ребром и плоскостью основания;

4) скалярное произведение векторов , где O - основание высоты пирамиды;

5) площадь вписанной в пирамиду сферу;

6) угол между ME, где E - середина BC, и плоскостью AMC.

Итоговое тестирование по стереометрии

См.: Звавич Л. И. Контрольные и проверочные работы по геометрии. 10-11 кл.: метод. пособие / Л. И. Звавич, А. Р. Рязановский, Е. В. Такуш. - М.: Дрофа, 2002.

1. Прямые α и b параллельны, а прямые α и c пересекаются. Каково взаимное расположение прямых b и c?

а) Пересекаются; б) скрещиваются; в) не параллельны; г) какое угодно.

2. Через три точки, лежащие на трех скрещивающихся ребрах куба, проведена плоскость. Найдите сумму внутренних углов многоугольника, получившегося в сечении.

а) 360°; б) 720°; в) 180°, или 360°, или 540°, или 720°.

3. Все боковые ребра пирамиды равны 13. Радиус окружности, вписанной в основание пирамиды, равен 5, а радиус окружности, описанной около основания пирамиды, равен 12. Найдите высоту пирамиды.

а) 12; б) 7; в) 5; г) невозможно определить, мало данных.

4. Все двугранные углы при ребрах основания четырехугольной пирамиды равны 45°. Радиус окружности, вписанной в основание пирамиды, равен 8, а радиус окружности, описанной около основания пирамиды, равен 52. Найдите высоту пирамиды.

а) 4; б) 8; в) 52; г) невозможно определить, мало данных.

5. Плоскости трех боковых граней треугольной пирамиды образуют с плоскостью ее основания угол 60°. Радиус окружности, вписанной в основание пирамиды, равен 8, а радиус окружности, описанной около основания пирамиды, равен 52. Найдите высоту пирамиды.

а) 4; б) 8; в) 26; г) невозможно определить, мало данных.

6. Расстояние между центрами двух сфер радиусов 4 и 7 равно 2. Опишите множество общих точек этих сфер.

а) Окружность; б) единственная точка; в) пустое множество; г) невозможно определить, мало данных.

7. Две образующие конуса взаимно перпендикулярны. Может ли угол в развертке конуса быть равен 252°?

а) Может; б) не может; в) две образующие конуса не могут быть взаимно перпендикулярны; г) невозможно определить, мало данных.

8. ABCD - осевое сечение цилиндра. B и C - точки верхнего основания, A и D - нижнего. Точка K делит дугу AD в отношении AK : KD = 1 : 2. Найдите величину угла AKC.

а) 90°; б) 60°; в) 30°; г) невозможно определить, мало данных.

9. Сечение, проходящее через середину бокового ребра пирамиды и параллельное основанию, разбило пирамиду на два тела, объем одного из которых на 6 м³ меньше, чем другого. Найдите объем пирамиды.

а) 28м³; б) 18 м³; в) 12 м³; г) невозможно определить, мало данных.

10. MABC - тетраэдр. Сколько существует различных плоскостей, от которых все вершины этого тетраэдра удалены на одно и то же расстояние?

а) 4; б) бесконечно много; в) 7; г) невозможно определить, мало данных.

11. При каком значении x длина вектора с координатами (1 - x; 4 + x; x) наименьшая?

а) -4; б) 0; в) -2; г) невозможно определить, мало данных.

12. Какую часть объема параллелепипеда ABCDA₁B₁C₁D₁ занимает объем тетраэдра A₁C₁BD?

а) Половину; б) треть; в) четверть; г) невозможно определить, мало данных.

13. Могут ли две плоскости несоседних боковых граней четырехугольной пирамиды быть перпендикулярны к плоскости основания?

а) Могут; б) не могут; в) у четырехугольной пирамиды нет несоседних боковых граней; г) невозможно определить, мало данных.

14. Расстояния от концов диаметра шара до касающейся его плоскости равны 3 см и 7 см. Найдите радиус шара.

а) 3; б) такая ситуация невозможна; в) 5; г) невозможно определить, мало данных.