- Учителю
- Практикум по комплексным числам и функциям
Практикум по комплексным числам и функциям
Министерство образования Московской области
Государственное бюджетное образовательное учреждение
среднего профессионального образования
Московской области
«Балашихинский промышленно-экономический колледж»
И.А. КАВЕРИНА
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО
ПЕРЕМЕННОГО
Учебно-методическое пособие
Балашиха 2015 г.
Каверина И.А. Теория функций комплексного переменного.- Учебно-методическое пособие. // Балашиха: Балашихинский промышленно-экономический колледж, 2015, 30 с..
Пособие разработано в соответствии с требованиями федерального государственного образовательного стандарта по специальности среднего профессионального образования 230115 «Программирование в компьютерных системах». Приводятся задачи для самостоятельного решения.
§1.1 Комплексные числа и действия над ними
Комплексными числами называются числа
вида ![]() , где
, где ![]() - действительные
числа,
- действительные
числа, ![]() - действительная
часть,
- действительная
часть, ![]() - мнимая часть
комплексного числа.
- мнимая часть
комплексного числа.
По определению, два комплексных числа: ![]() и
и ![]() - равны тогда и
только тогда, когда
- равны тогда и
только тогда, когда ![]() и
и
![]() .
.
Комплексное число ![]() называется
сопряженным комплексному числу
называется
сопряженным комплексному числу ![]() , если
, если ![]() . Другими словами,
если
. Другими словами,
если ![]() , то
, то ![]() .
.
Всякому комплексному числу ![]() можно поставить в
соответствие единственную точку плоскости
можно поставить в
соответствие единственную точку плоскости ![]() и обратно, всякую
точку
и обратно, всякую
точку ![]() плоскости
плоскости ![]() можно рассматривать
как геометрический образ единственного комплексного числа
можно рассматривать
как геометрический образ единственного комплексного числа ![]() .y
.y
М
0 х
Рисунок 1
Для сокращения вместо "точка, соответствующая
комплексному числу ![]() ",
говорят просто "точка
",
говорят просто "точка ![]() ". При
этом множество всех действительных чисел изображается точками оси
абсцисс, которая поэтому называется действительной осью, множество
чисто мнимых чисел
". При
этом множество всех действительных чисел изображается точками оси
абсцисс, которая поэтому называется действительной осью, множество
чисто мнимых чисел ![]() точками оси ординат, называемой мнимой осью. Заметим, что одна
точка мнимой оси, а именно начало коорди-
точками оси ординат, называемой мнимой осью. Заметим, что одна
точка мнимой оси, а именно начало коорди-
нат, изображает действительное число нуль. Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.
В некоторых случаях удобно считать
геометрическим изображением числа ![]() радиус-вектор точки
радиус-вектор точки
![]() -
- ![]() .
.
y
0 z3
5 x
-2 z2
-5 z1
Рисунок 2
Пример 1. Построить точки ![]() ,
, ![]() ,
, ![]() .
.
В дальнейшем, наряду с представлением комплексных чисел в декартовых координатах, полезно иметь их представление в обобщенных полярных координатах.
Рассмотрим число ![]() , которому на
плоскости соответствует точка
, которому на
плоскости соответствует точка ![]() .
Ее координаты в полярной системе координат
.
Ее координаты в полярной системе координат ![]() .
.
y
M(x; y)
ρ
φ
0 x
Рисунок 3
Тогда ![]()
![]() .
.
![]()
![]() .
.
Полярный радиус ![]() называется
модулем комплексного числа и обозначается
называется
модулем комплексного числа и обозначается ![]() .
.
Полярный угол ![]() называется
аргументом комплексного числа и обозначается
называется
аргументом комплексного числа и обозначается ![]() . Тогда
. Тогда
![]() .
.
Эта форма называется тригонометрической формой комплексного числа.
Модуль комплексного числа определяется
однозначно: ![]() .
.
Аргумент комплексного числа определяется с
точностью до слагаемого, кратного ![]() . Главным значением
аргумента называется значение, заключенное в интервале
. Главным значением
аргумента называется значение, заключенное в интервале ![]() . Обозначается оно
. Обозначается оно
![]() . Таким образом,
. Таким образом,
![]() .
.
Очевидно, ![]() .
.
Главное значение аргумента определяется однозначно.
Так как ![]() ,
,
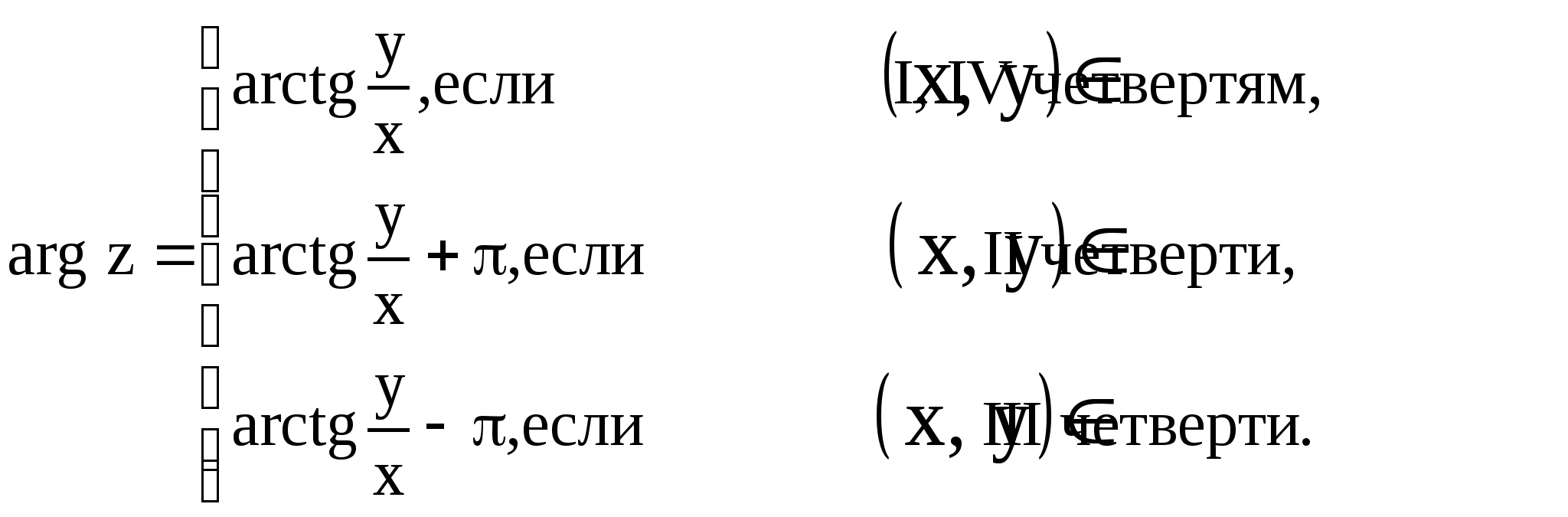
Тригонометрическая форма комплексного числа будет иметь вид
![]() .
.
Пример 2. Написать в тригонометрической
форме комплексное число ![]() .
.
 y
y
z 1
-1 0 x
Рисунок 4
Решение. ![]()
![]()
![]()
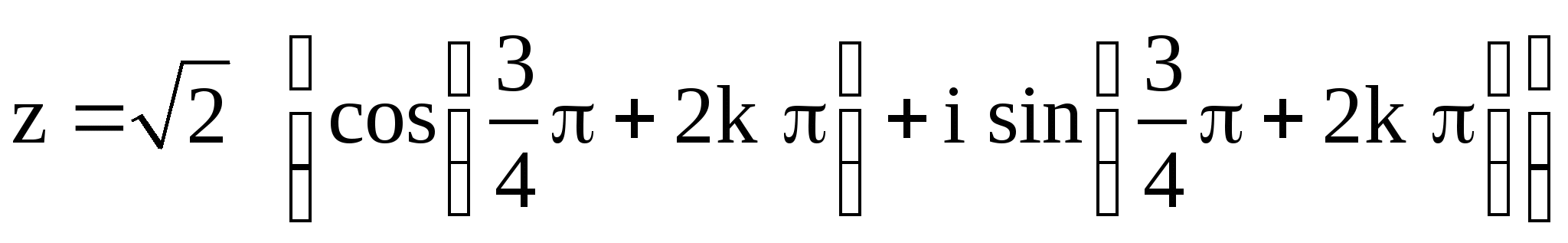 .
.
Пусть ![]() .
Используя формулу Эйлера
.
Используя формулу Эйлера ![]() ,
получаем так называемую показательную форму записи
комплексного числа:
,
получаем так называемую показательную форму записи
комплексного числа:
![]() .
.
Пример 3. Представить в показательной
форме комплексное число ![]() .y
.y
-1 0
x
z -1
Рисунок 5
Решение
![]()
![]()
![]()
Пример 4. Вычислить ![]() .
.
Решение. По формуле Эйлера ![]() .
.
§1.2 Алгебраические действия над комплексными числам
Сложение и умножение комплексных чисел
производится по правилам сложения и умножения алгебраических
многочленов с учетом ![]() . При
записи результата следует отделить действительную часть от мнимой,
т. е. собрать отдельно члены, содержащие множитель
. При
записи результата следует отделить действительную часть от мнимой,
т. е. собрать отдельно члены, содержащие множитель ![]() , и члены, не
содержащие множитель
, и члены, не
содержащие множитель ![]() :
:
![]()
![]()
![]()
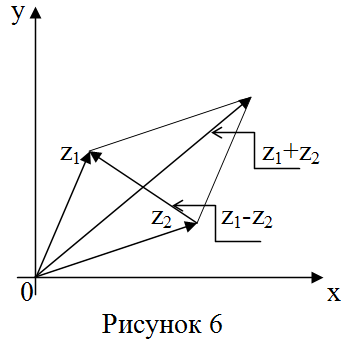
В частности, ![]() . Операции сложения и
вычитания сводятся к сложе- нию и вычитанию векторов, изображающих
эти числа. Отсюда расстояние между точками
. Операции сложения и
вычитания сводятся к сложе- нию и вычитанию векторов, изображающих
эти числа. Отсюда расстояние между точками ![]() .
.
Пример 5. ![]() - уравнение
окружности с центром в точке
- уравнение
окружности с центром в точке ![]() и радиусом равным
и радиусом равным ![]() .
.
Деление на комплексное число, отличное от нуля, определяется как действие, обратное умножению. Для представления частного в виде
![]()
следует провести простые преобразования, показанные на следующем примере.
Пример 6.
 .
.
Для модуля и аргумента произведения и частного справедливы следующие утверждения:
1. ![]()
Пример 7. Найти модуль и аргумент
произведения ![]() .
.
Решение. 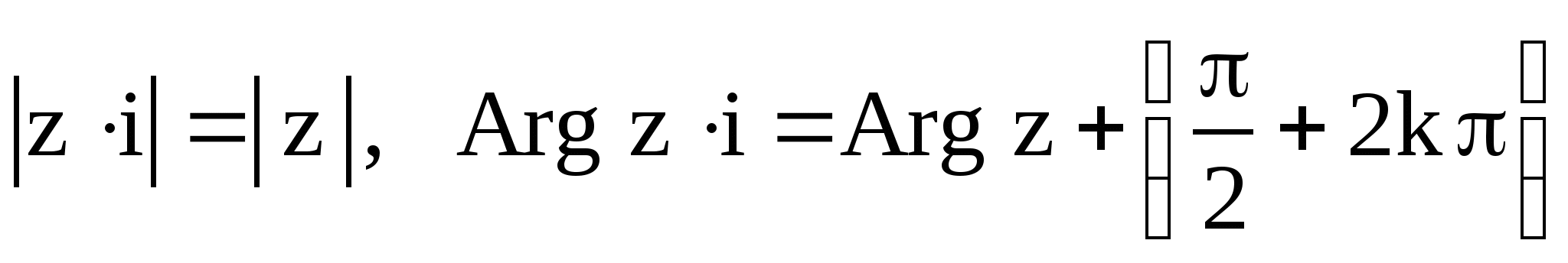 .
.
Таким образом, умножение на ![]() соответствует
повороту вектора
соответствует
повороту вектора ![]() на угол
на угол
![]() ;
;
2. 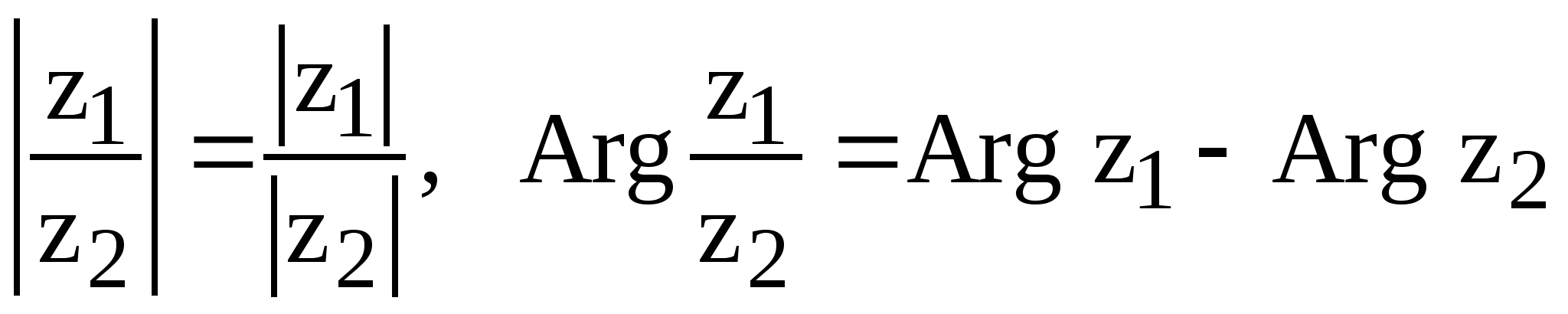 .
.
Пусть ![]() .
.
Тогда ![]() .
.
Можно доказать методом полной математической
индукции, что для любого целого ![]() (формула Муавра).
Формула справедлива и для целых отрицательных
(формула Муавра).
Формула справедлива и для целых отрицательных ![]() .
.
Пример 8. Вычислить ![]() .
.
y
![]()
0 x
-1 z
Рисунок 7
Решение
![]()
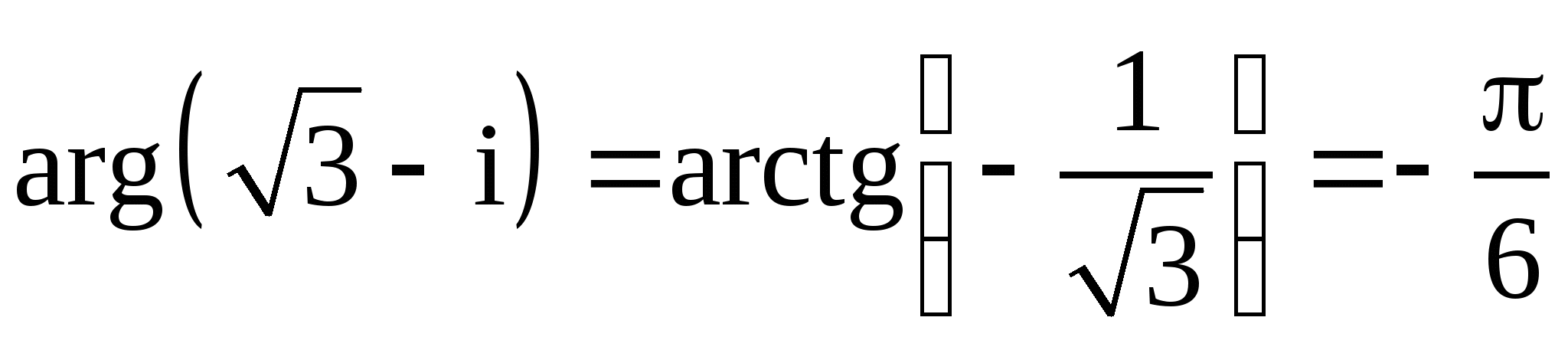 ,
,
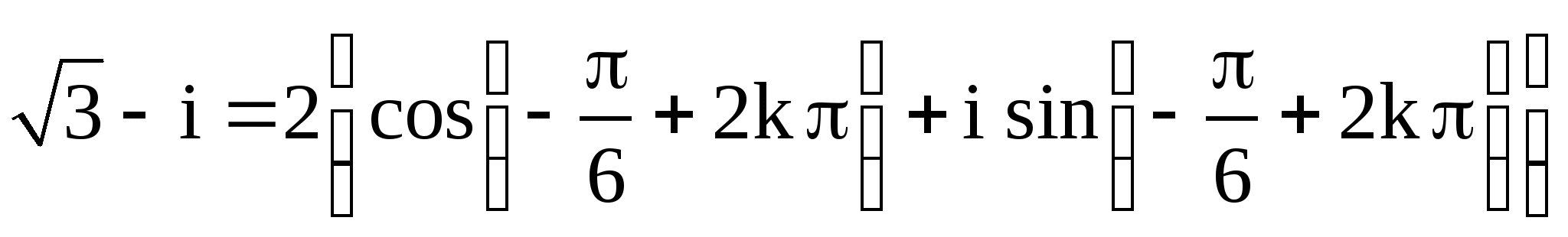 ,
,
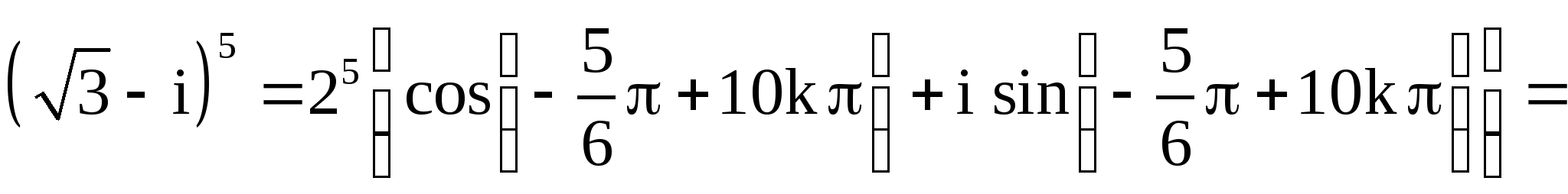
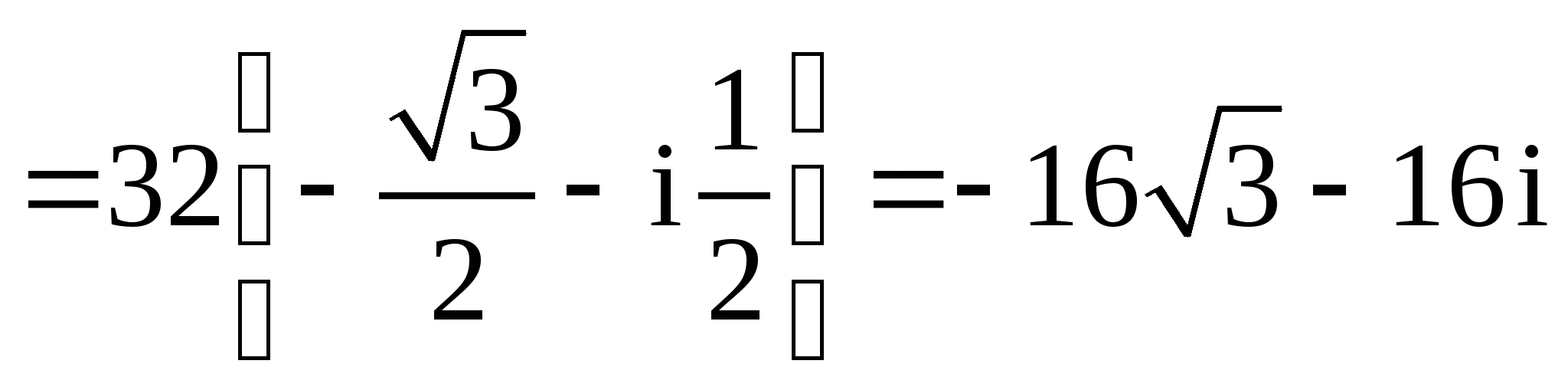 .
.
Корнем ![]() -й
степени из комплексного числа называется такое число
-й
степени из комплексного числа называется такое число ![]() , для которого
, для которого
![]() .
.
Используя формулу Муавра, получим
![]()
Для других значений ![]() аргументы будут
отличаться от полученных на число кратное
аргументы будут
отличаться от полученных на число кратное ![]() , и, следовательно,
получатся значения корня, совпадающие с рассмотренными. Итак,
корень
, и, следовательно,
получатся значения корня, совпадающие с рассмотренными. Итак,
корень ![]() -й степени из
комплексного числа имеет
-й степени из
комплексного числа имеет ![]() различных значений.
различных значений.
Пример 9. Найти все значения ![]() и построить
их.
и построить
их.
y
![]()

![]() φ x
φ x
![]()
Рисунок 8
Решение. ![]() ,
,
![]() ,
,
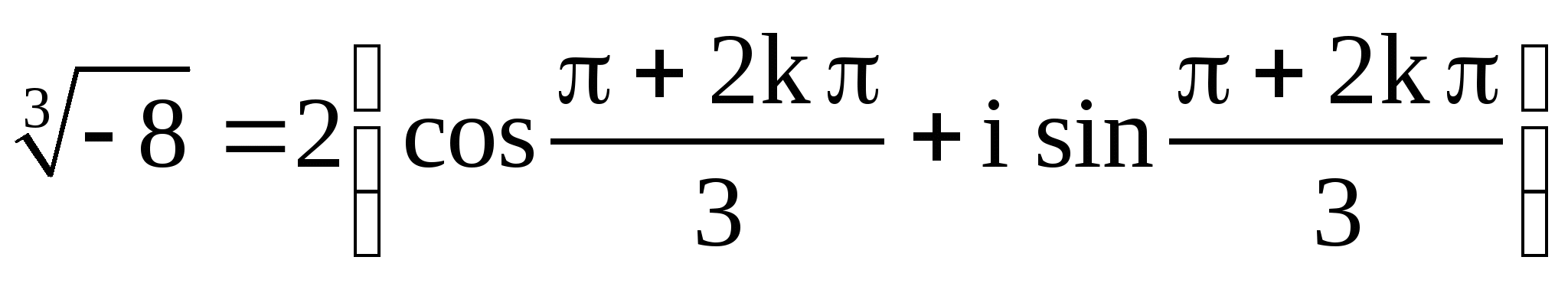 ,
,
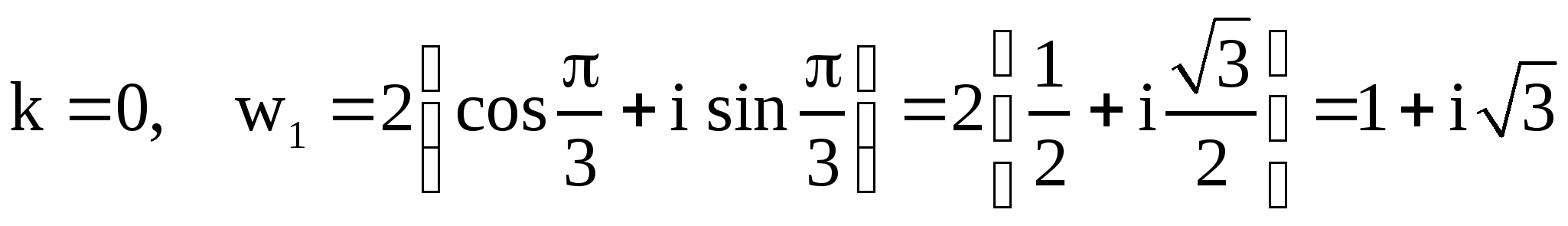 ,
,
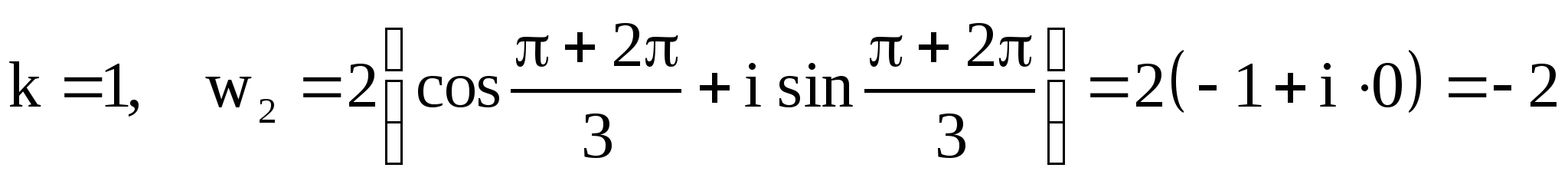 ,
,
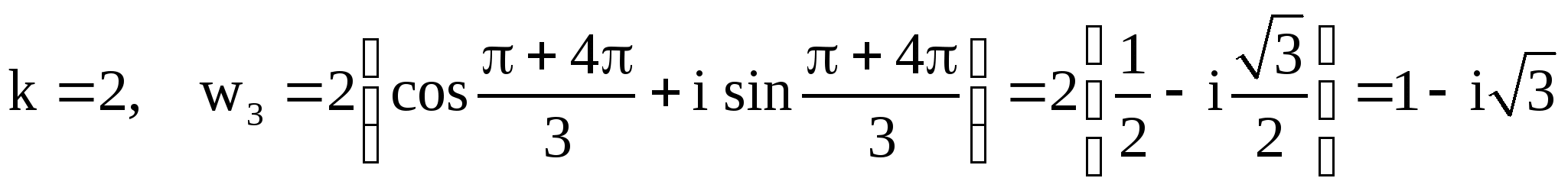 .
.
§1.3 Понятие функции комплексного переменного. Элементарные функции
Говорят, что на множестве ![]() точек плоскости
точек плоскости
![]() задана функция
задана функция
![]() , если указан закон,
по которому каждой точке
, если указан закон,
по которому каждой точке ![]() из
из
![]() ставится в
соответствие определенная точка или совокупность точек
ставится в
соответствие определенная точка или совокупность точек ![]() .
.
В первом случае функция ![]() называется
однозначной, во втором - многозначной. В дальнейшем, если не будет
оговорено противное, под функцией будем понимать однозначную
функцию.
называется
однозначной, во втором - многозначной. В дальнейшем, если не будет
оговорено противное, под функцией будем понимать однозначную
функцию.
Если положить ![]() и
и ![]() , то задание функции
комплексного переменного
, то задание функции
комплексного переменного ![]() будет
равносильным заданию двух функций двух действительных переменных:
будет
равносильным заданию двух функций двух действительных переменных:
![]() .
.
Функции комплексного переменного ![]() определяются как
суммы следующих рядов, сходящихся на всей комплексной плоскости:
определяются как
суммы следующих рядов, сходящихся на всей комплексной плоскости:
На действительной оси ![]() эти функции совпадают
с соответствующими элементарными функциями действительного
переменного.
эти функции совпадают
с соответствующими элементарными функциями действительного
переменного.
Для функции комплексного переменного справедлива формула Эйлера:
![]() .
.
Из этой формулы следует, что
Остаются справедливыми при комплексных значениях аргумента все
тригонометрические тождества.
Основное свойство показательной функции
![]() также сохраняется. В
частности,
также сохраняется. В
частности,
![]()
Функции ![]() (
(![]() - целое положительное
число),
- целое положительное
число), ![]()
![]() определяются как
обратные функции по отношению к
определяются как
обратные функции по отношению к ![]()
![]()
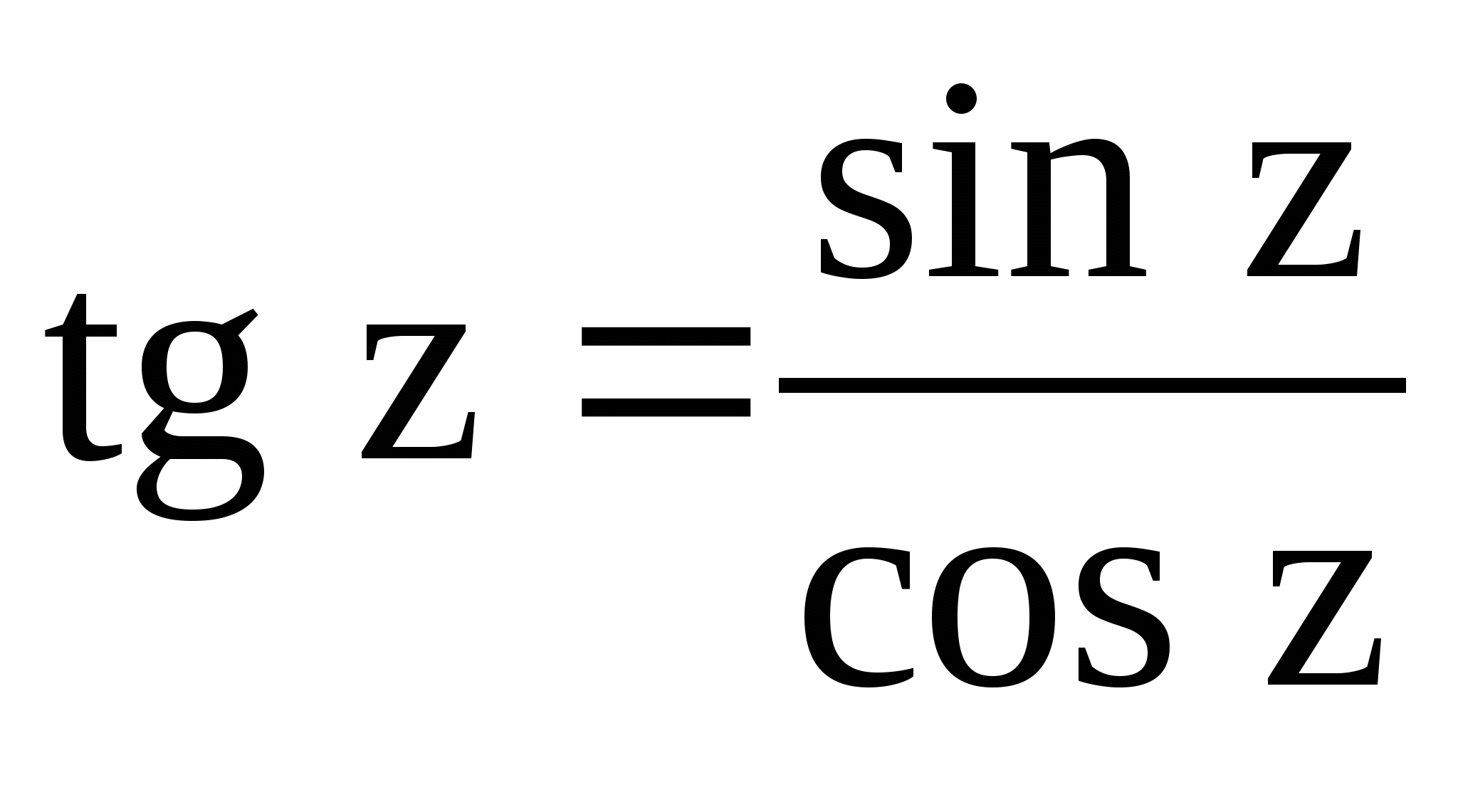 и
являются многозначными функциями.
и
являются многозначными функциями.
Можно показать, что
![]()
В этом выражении при каждом фиксированном
![]() получаем однозначные
функции, которые называются ветвями,
получаем однозначные
функции, которые называются ветвями, ![]() называется главной
ветвью функции
называется главной
ветвью функции ![]() .
.
![]() ;
;
![]() ;
;
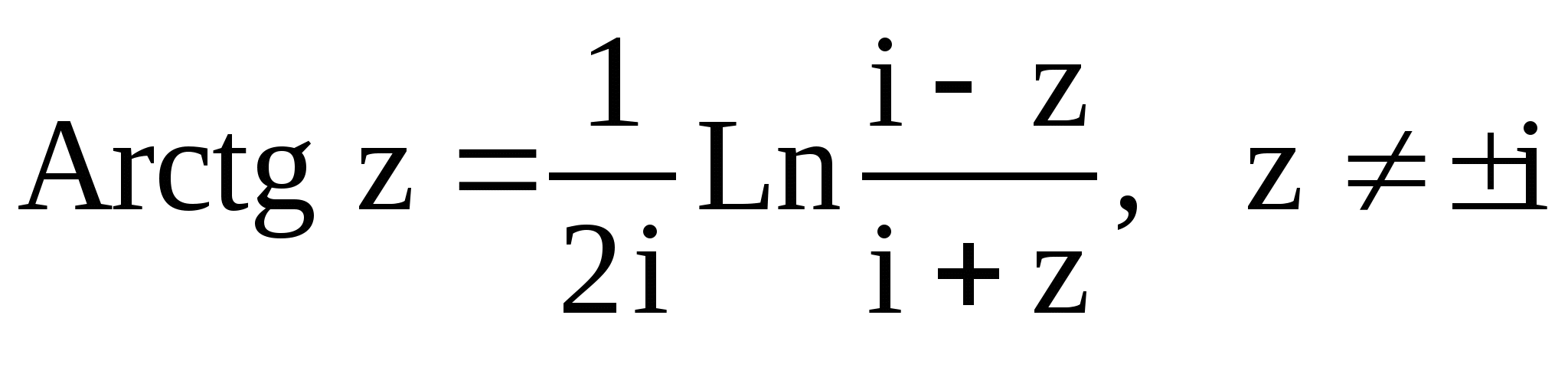 .
.
Степень с комплексным основанием ![]() и комплексным
показателем
и комплексным
показателем ![]() определяется
равенством
определяется
равенством
![]() .
.
Пример 1. Вычислить значения функций:
а) ![]() в
точке
в
точке ![]() .
.
Решение 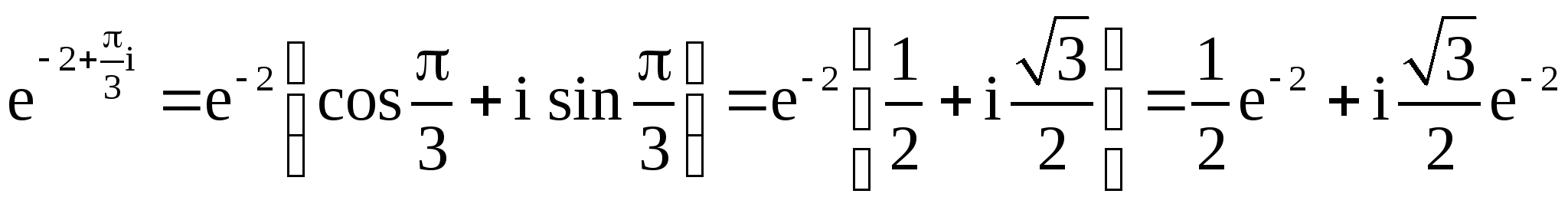 .
.
б) ![]() в
точке
в
точке ![]() .
.
Решение ![]()
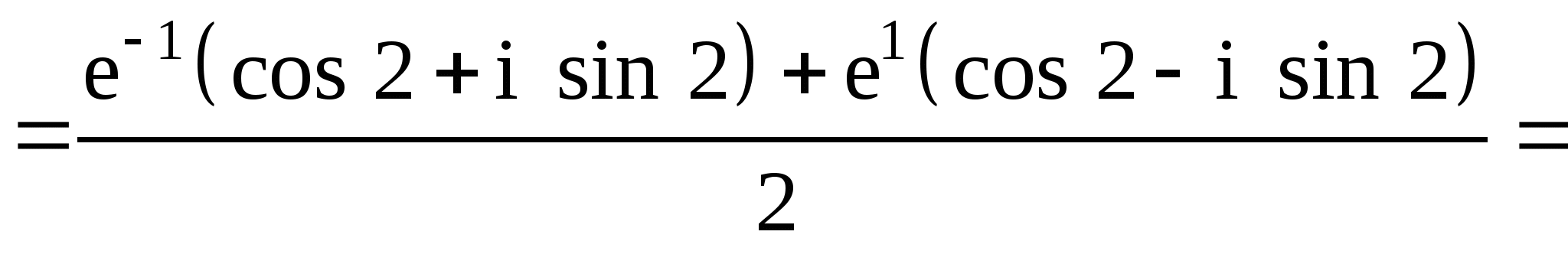
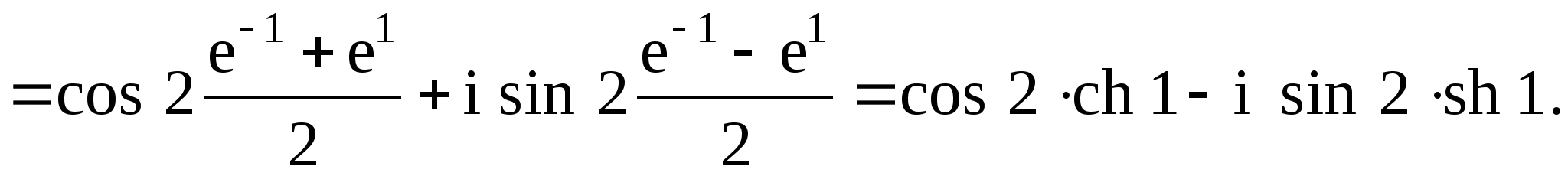
Или, учитывая, что ![]() , получим
, получим
![]()
в) ![]() в
точке
в
точке ![]() .
.
Решение
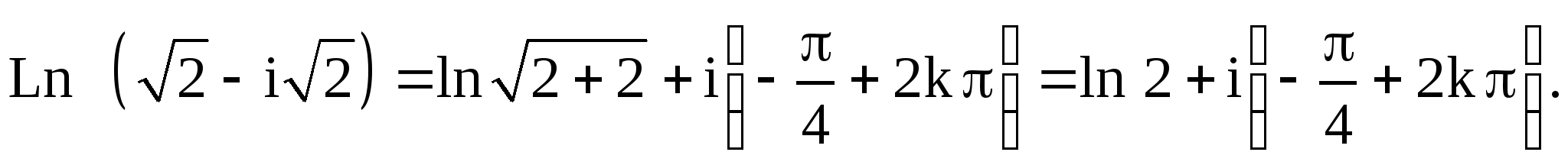
Пример 2. Вычислить ![]() .
.
Решение
![]()
![]()
Условимся откладывать значения ![]() на одной комплексной
плоскости, а значения
на одной комплексной
плоскости, а значения ![]() - на
другой. Тогда однозначную функцию комплексного переменного можно
рассматривать как отображение множества
- на
другой. Тогда однозначную функцию комплексного переменного можно
рассматривать как отображение множества ![]() плоскости
плоскости ![]() на множество
на множество
![]() плоскости
плоскости ![]() . Если при этом двум
различным точкам
. Если при этом двум
различным точкам ![]() всегда
соответствуют различные точки
всегда
соответствуют различные точки ![]() ,
то такое отображение называется взаимно однозначным или однолистным
в
,
то такое отображение называется взаимно однозначным или однолистным
в ![]() .
.
Пример 3. При отображении ![]() найти образ линии
найти образ линии
![]() .
.
Решение. Так как ![]() , исключим
, исключим ![]() из системы:
из системы:
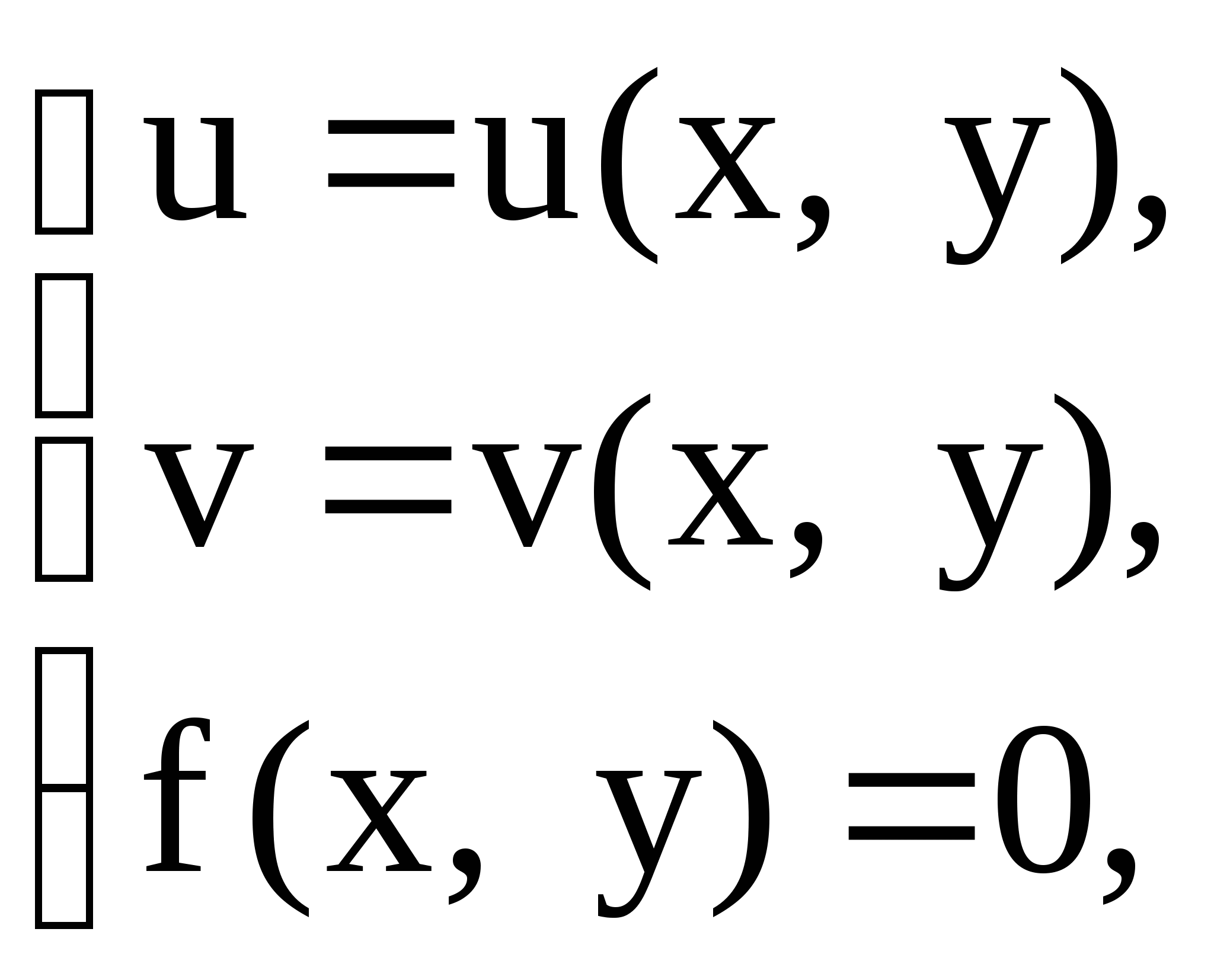
где ![]() -
уравнение линии в плоскости
-
уравнение линии в плоскости ![]() .
.
Найдем искомую зависимость, связывающую
![]() и
и ![]() .
.
![]()
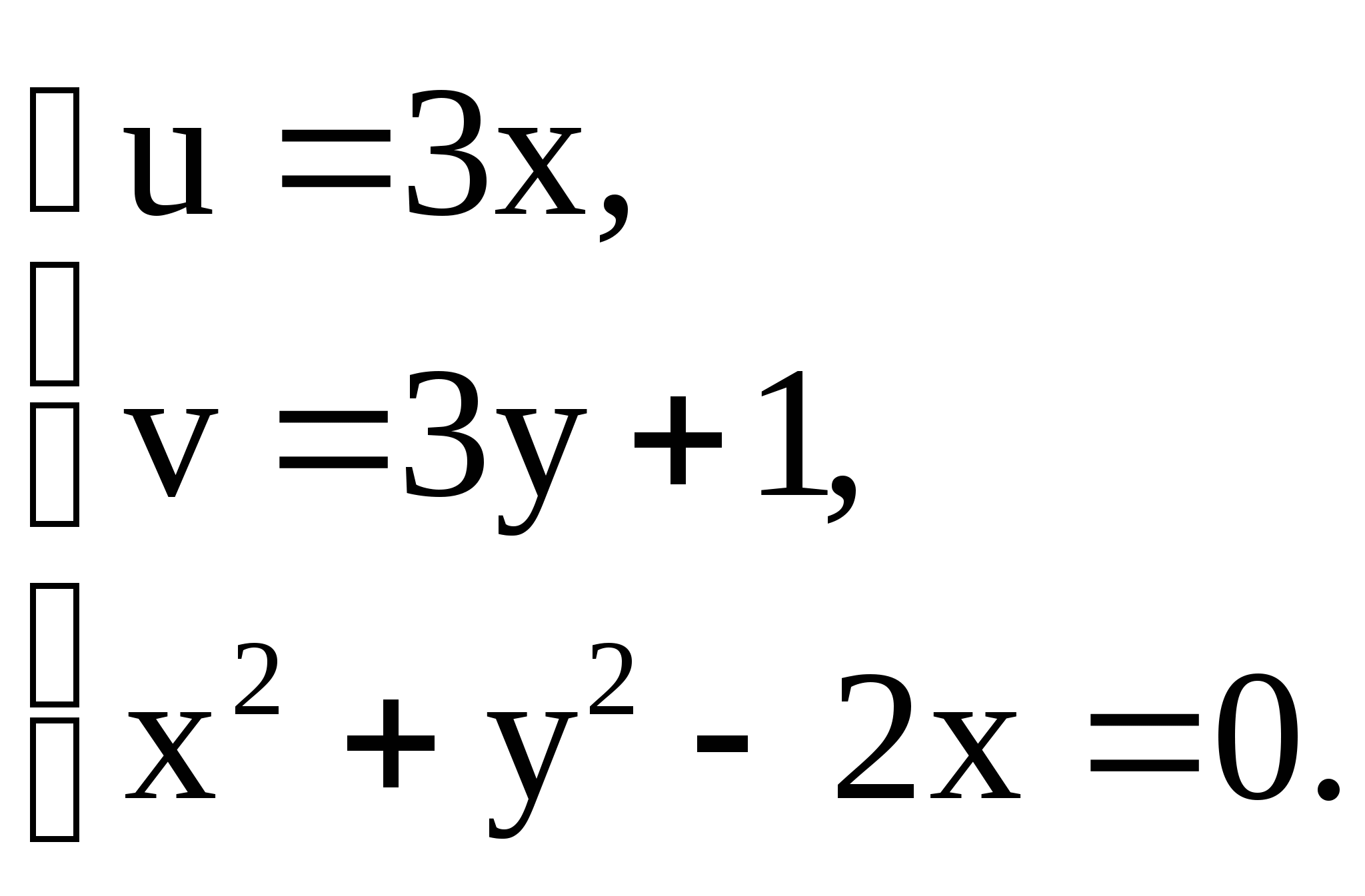
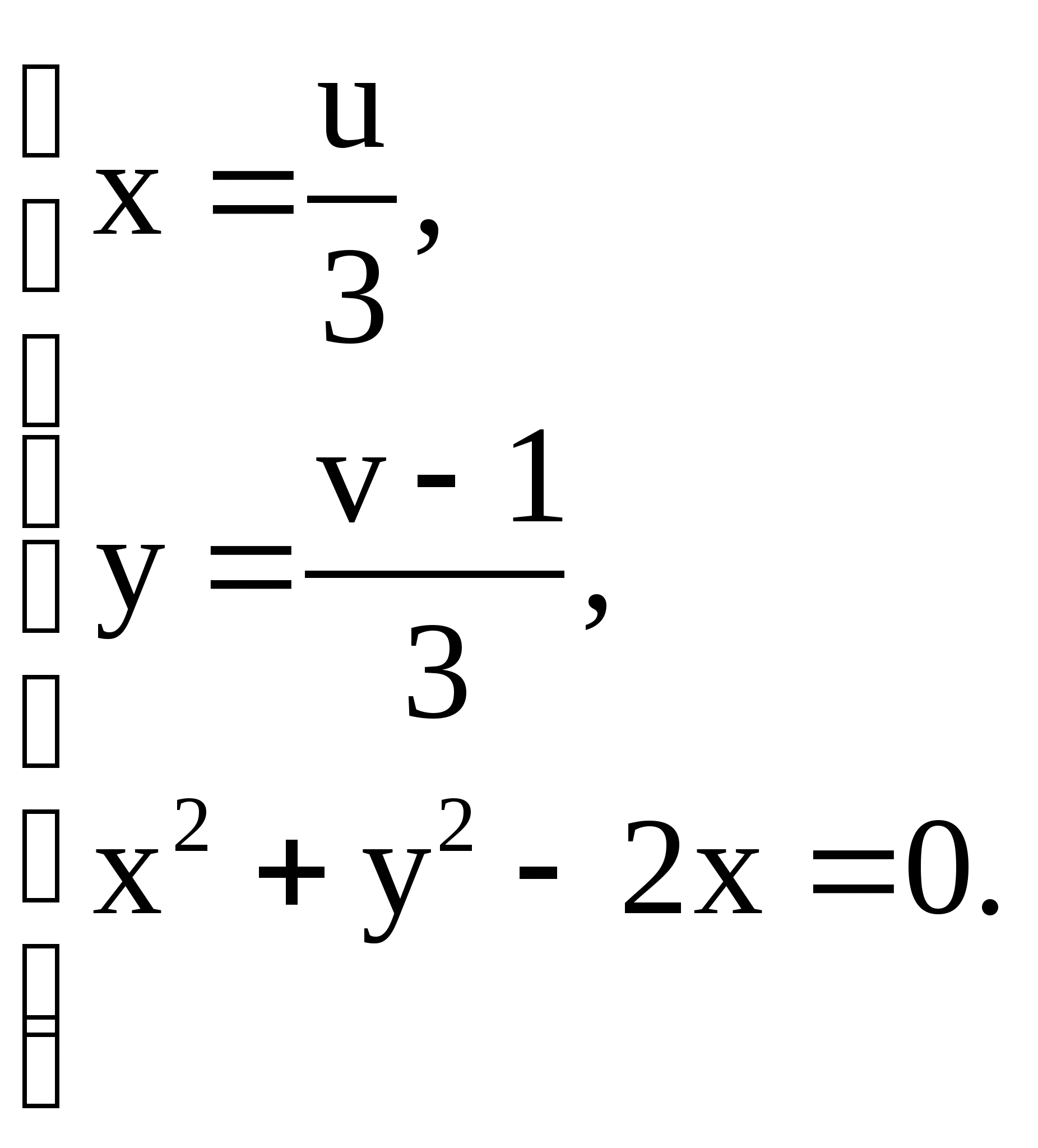
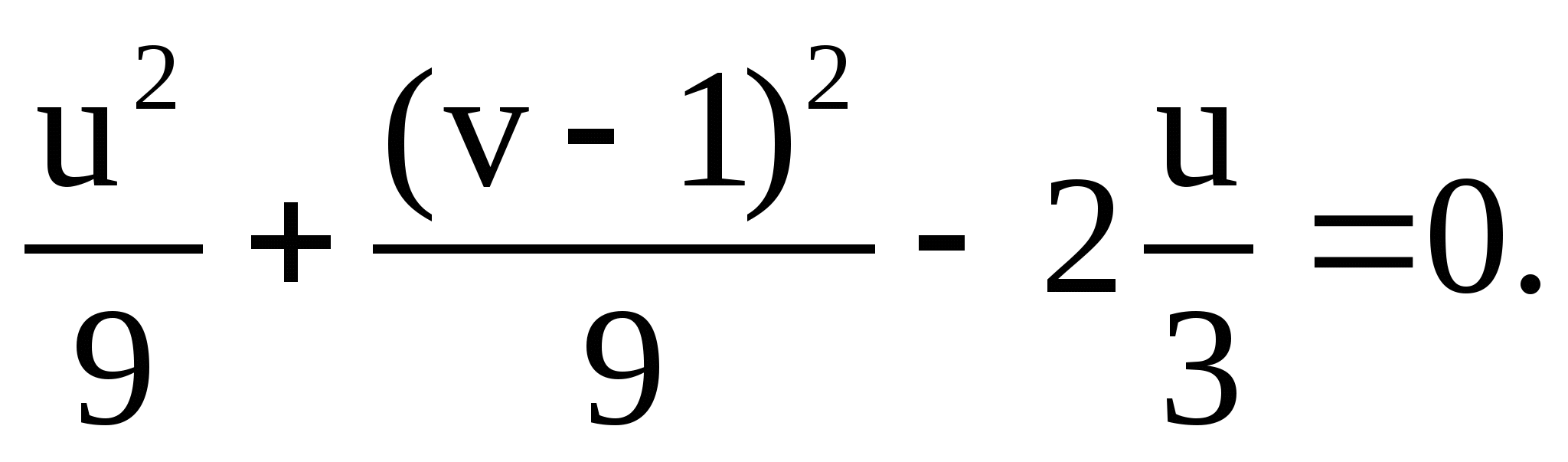
Преобразуя уравнение 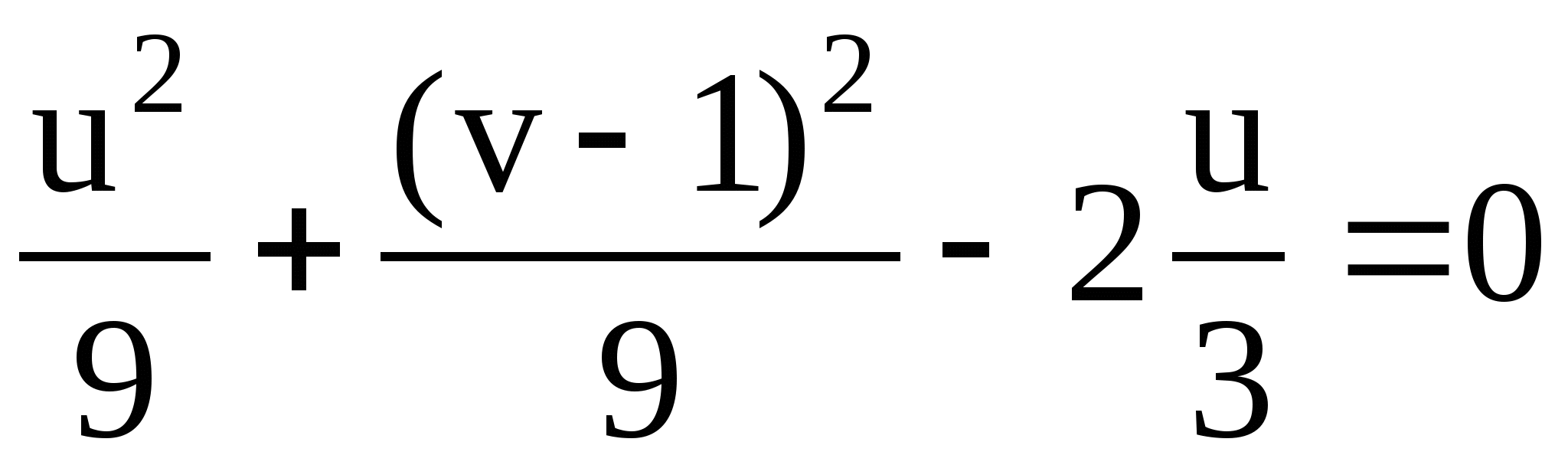 , получим
, получим
![]() .
.
Таким образом, окружность ![]() в плоскости
в плоскости ![]() отображается в
окружность
отображается в
окружность ![]() в плоскости
в плоскости
![]() .
.
Пример 4. При отображении ![]() найти образ полярной
сетки полуплоскости
найти образ полярной
сетки полуплоскости ![]() .
.
Решение
-
Найдем образы полуокружностей (рис. 8):
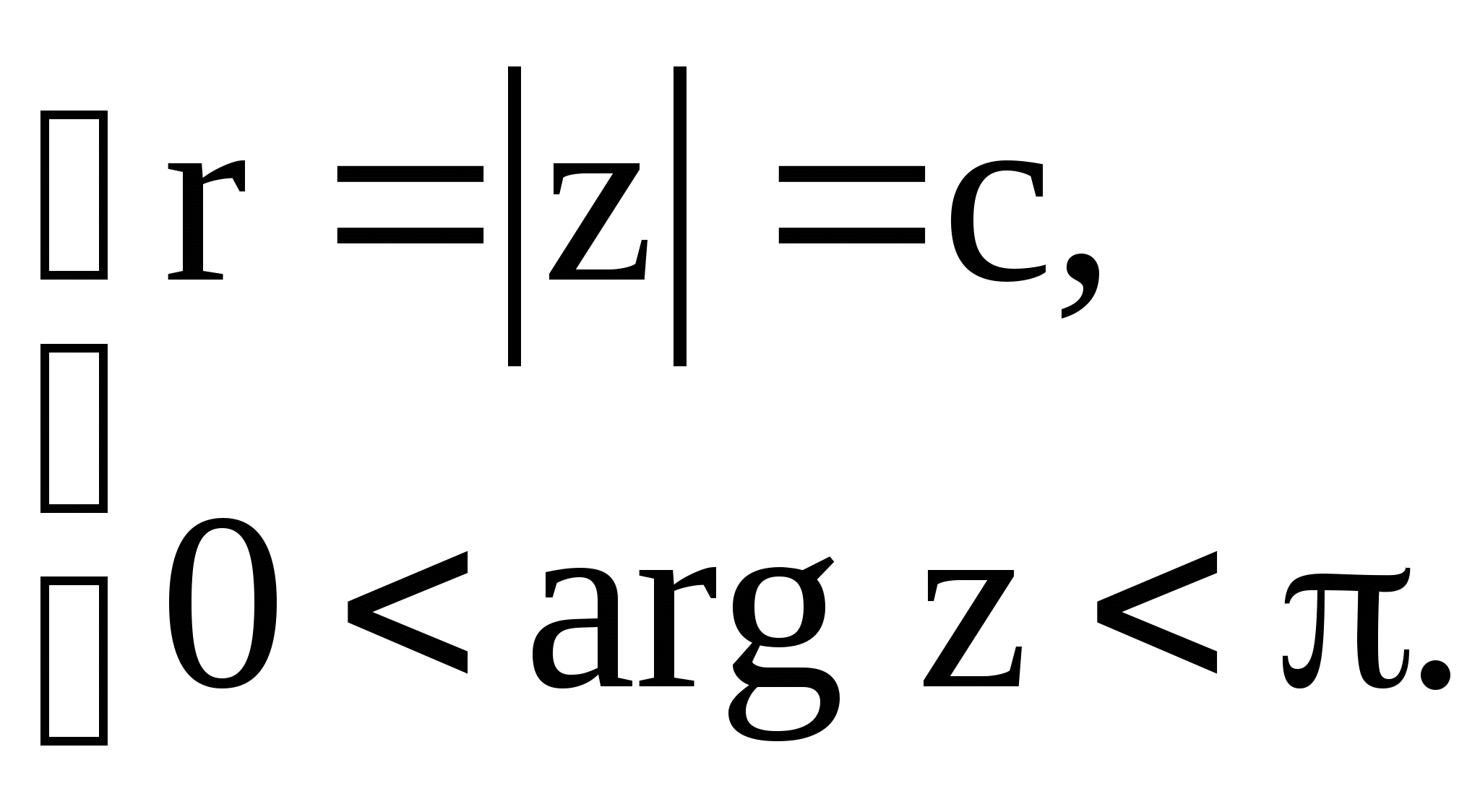
![]()
Образы-окружности ![]() с удаленной точкой
с удаленной точкой
![]() .
.
y
Рисунок 8
0 x
-
Найдем образы лучей (рис. 9)
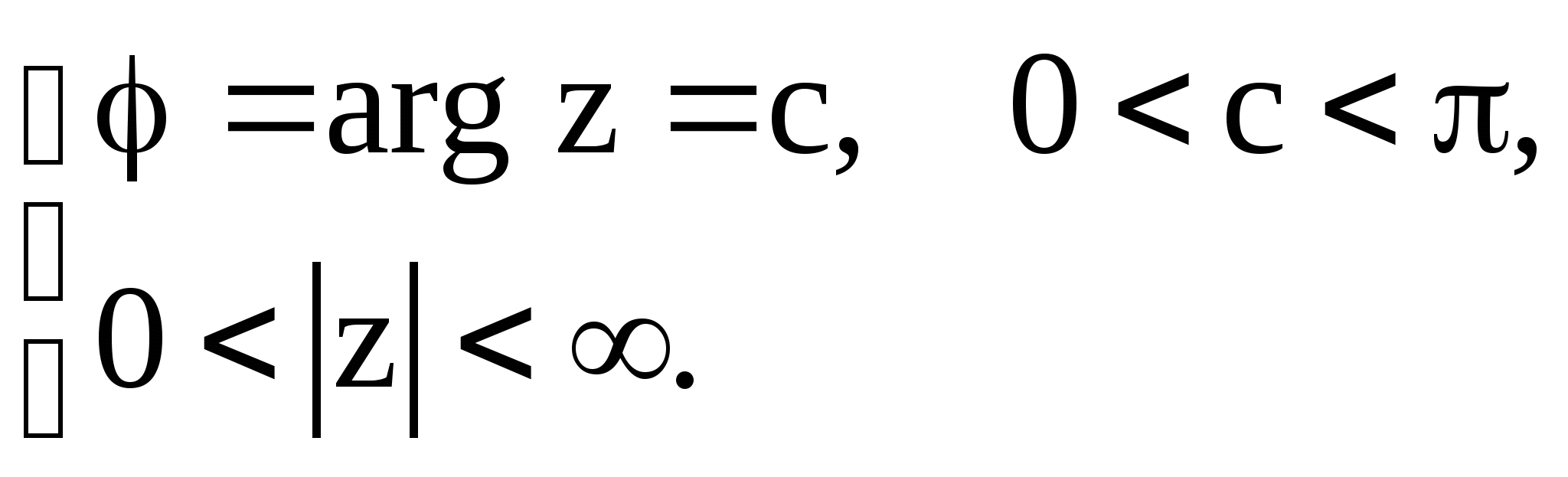
![]()
Образы-лучи с удаленной точкой ![]() .
.
-
v



Рисунок 9


0 u
Следовательно, образом полярной сетки
полуплоскости ![]() является полярная
сетка плоскости
является полярная
сетка плоскости ![]() с разрезом
вдоль положительной полуоси
с разрезом
вдоль положительной полуоси ![]() (рис. 9).
(рис. 9).
§1.4 Задачи
1.1. Вычислить значения функций:
а) ![]() в
точках
в
точках ![]()
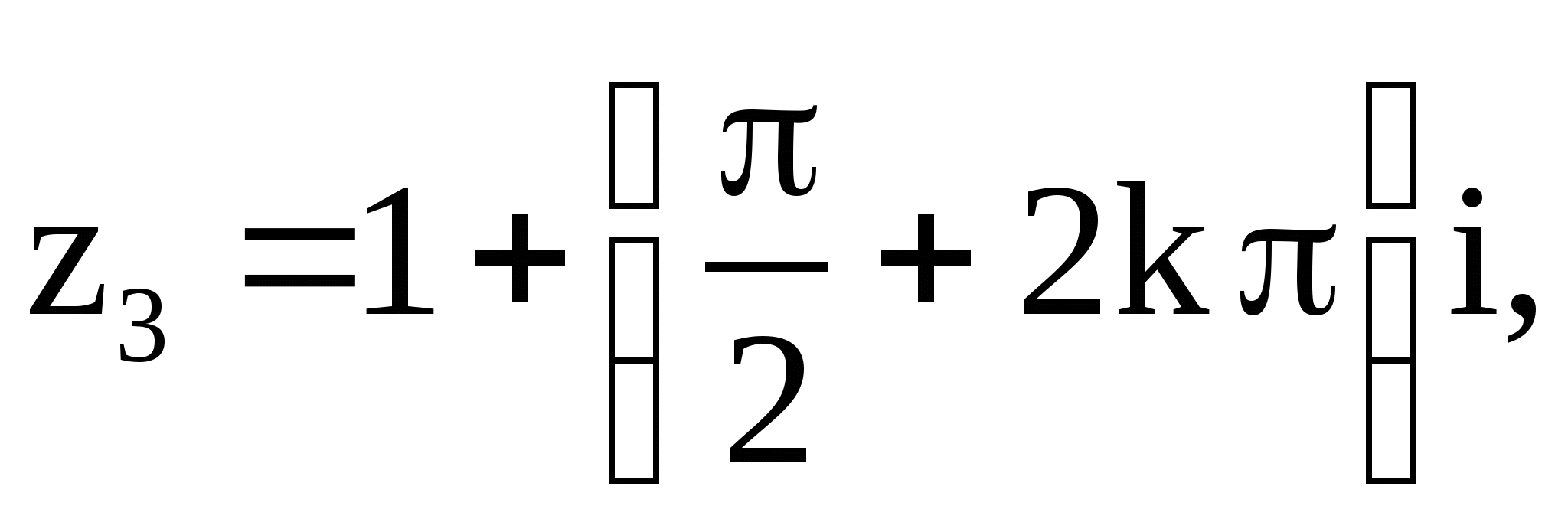 где
где ![]() - целое число;
- целое число;
б) ![]() в
точках
в
точках ![]() ;
;
в) ![]() в
точках
в
точках ![]() ;
;
г) ![]() в
точках
в
точках ![]() ;
;
д) ![]() в
точках
в
точках ![]() ;
;
е) ![]() в
точках
в
точках ![]() .
.
1.2. Вычислить ![]()
1.3. Вычислить ![]() , подсчитав
действительную и мнимую части с точностью до 0,0001.
, подсчитав
действительную и мнимую части с точностью до 0,0001.
1.4. Вычислить действительные и мнимые
части функций: а) ![]() ; б)
; б)
![]() ;
;
в) ![]() .
.
1.5. Решить уравнение: ![]() .
.
1.6. Доказать тождества:
а) ![]() б)
б)
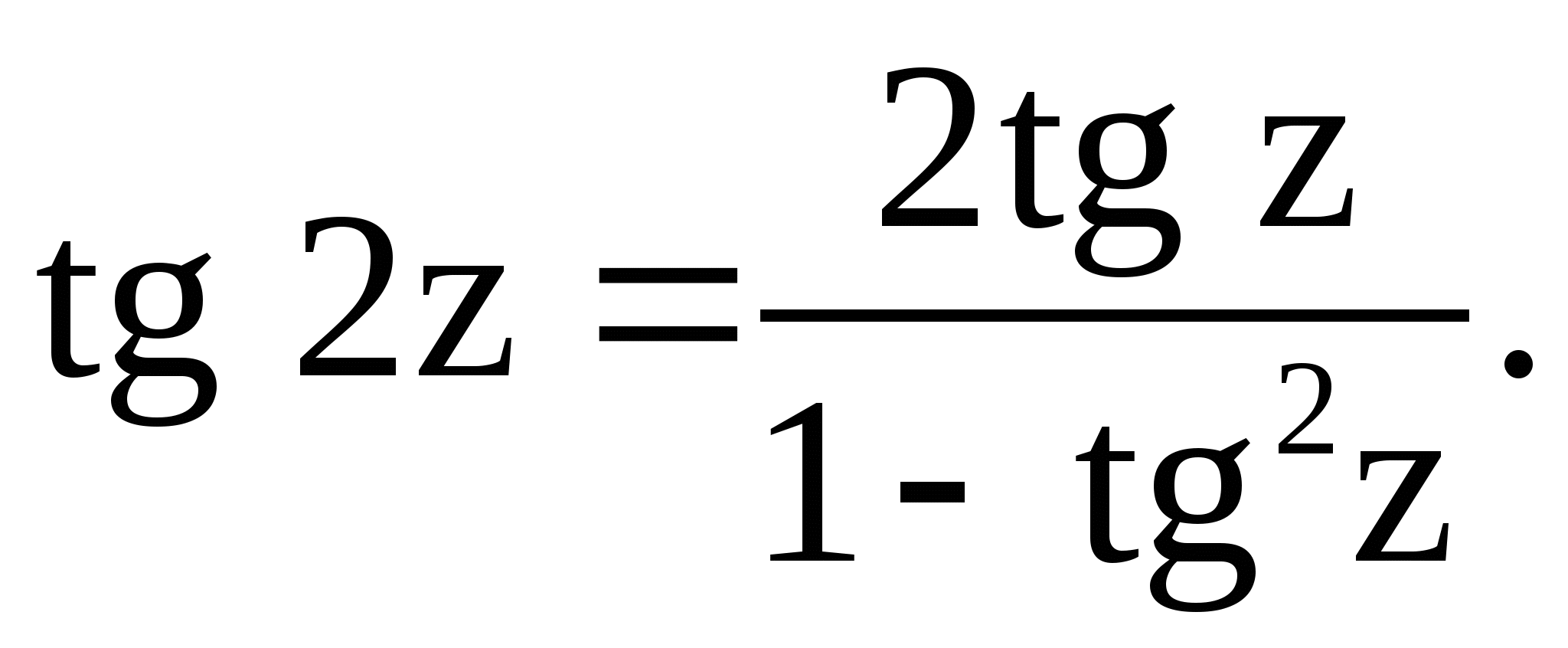
1.7. Построить на комплексной плоскости
образы точки ![]() при отображениях:
а)
при отображениях:
а) ![]() б)
б) ![]() в)
в) ![]()
1.8. При отображении ![]() найти образ линии
найти образ линии
![]()
1.9. При отображении ![]() найти образ
прямоугольной сетки полуплоскости
найти образ
прямоугольной сетки полуплоскости ![]()
1.10. При отображении, осуществляемом
функцией Жуковского 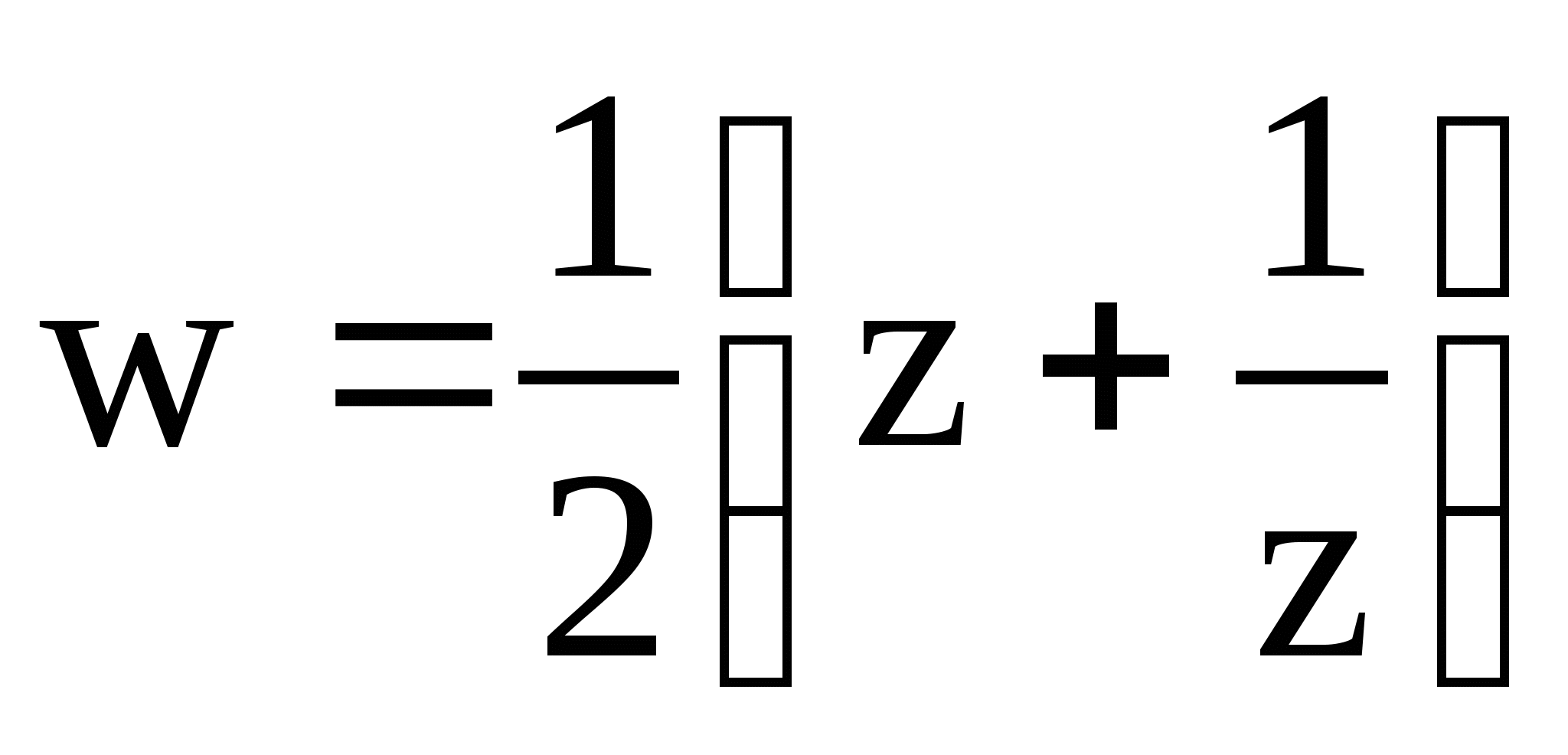 ,
найти образ линии
,
найти образ линии ![]()
§1.5 Задачи для самостоятельного решения
1.11. Вычислить значения функций:
а) ![]() в
точках
в
точках ![]()
б) ![]() в
точках
в
точках ![]()
в) ![]() в
точках
в
точках ![]()
г) ![]() в
точках
в
точках ![]()
д) ![]() в
точках
в
точках 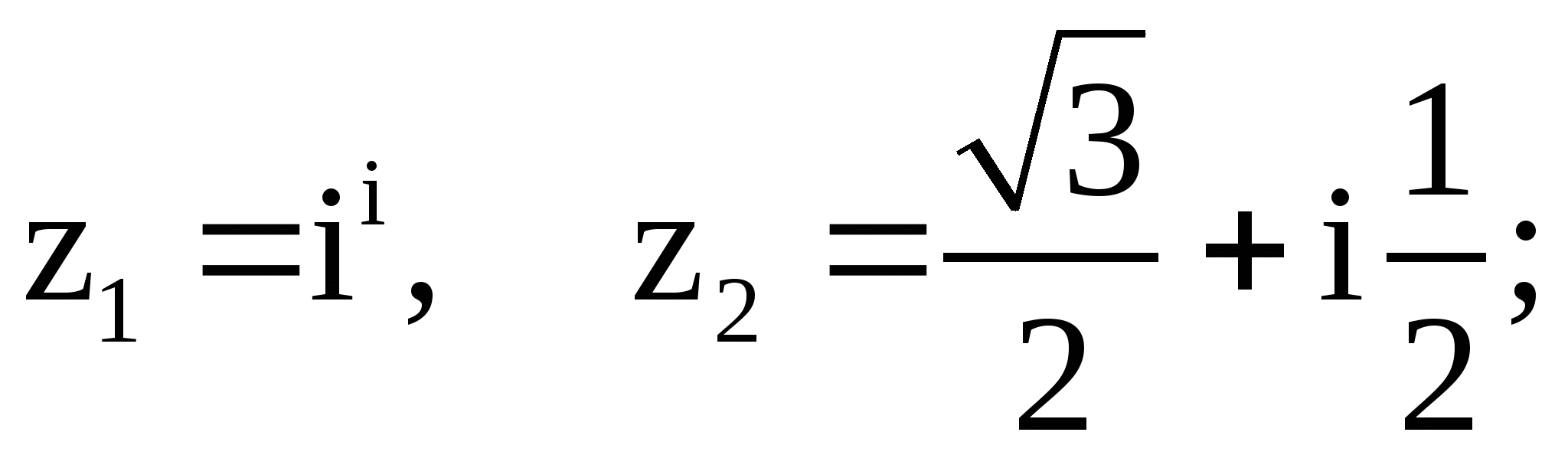
е) ![]() в
точках
в
точках ![]()
1.12. Вычислить 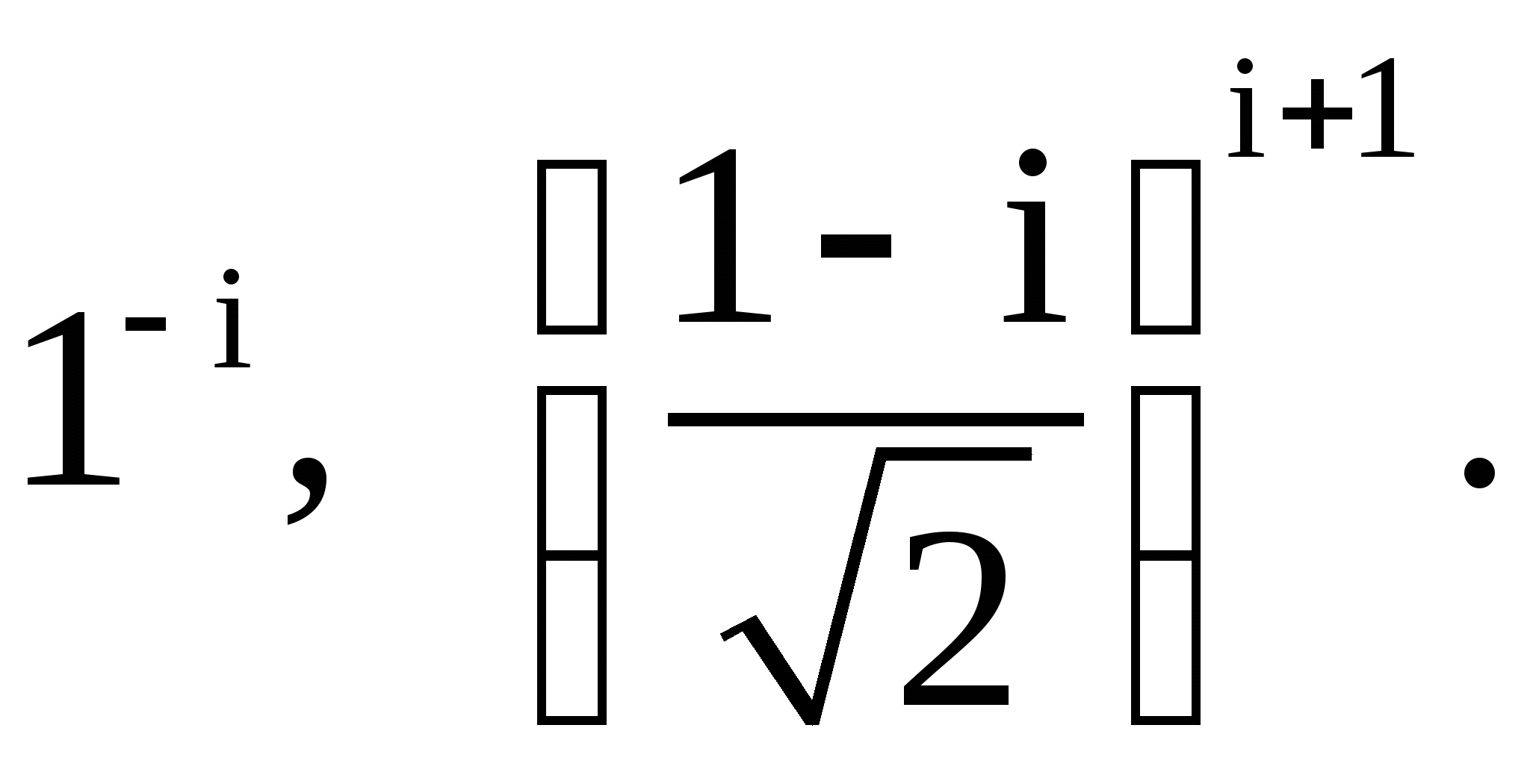
1.13. Вычислить ![]() , подсчитав
действительную и мнимую части с точностью до
, подсчитав
действительную и мнимую части с точностью до ![]() .
.
1.14. Вычислить действительные и мнимые
части функций: а) ![]()
б) ![]() в)
в)
![]()
1.15. Доказать тождества:
а) ![]()
б) ![]()
1.16. При отображении ![]() найти образ линии
найти образ линии
![]()
1.17. При отображении 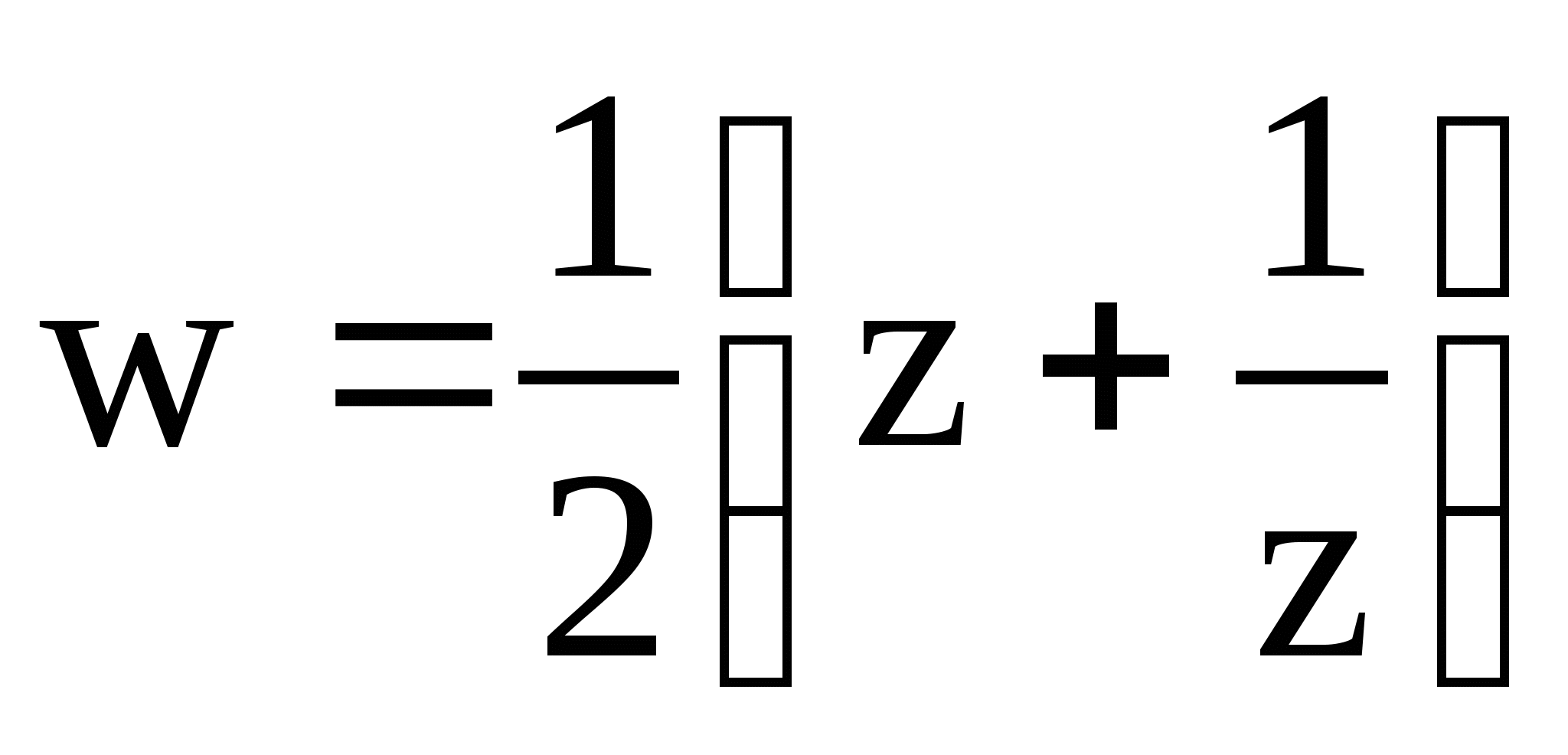 найти образ линии
найти образ линии
![]()
1.18. При отображении ![]() найти прообраз
прямоугольной сетки плоскости
найти прообраз
прямоугольной сетки плоскости ![]() с разрезом вдоль положительного направления действительной оси.
с разрезом вдоль положительного направления действительной оси.
§2.1 Производная функции комплексного переменного
Комплексное число ![]() называется
пределом функции
называется
пределом функции ![]() при
при
![]() , стремящемся к
, стремящемся к
![]() , если для любого
, если для любого
![]() существует такое
существует такое
![]() , что как только
, что как только
![]() .
.
Отсюда следует, что если ![]() и
и ![]() , то
, то
![]()
Верно и обратное утверждение.
Функция ![]() называется непрерывной в точке
называется непрерывной в точке ![]() , если
, если
![]() .
.
Производной функции комплексного
переменного ![]() называется
называется
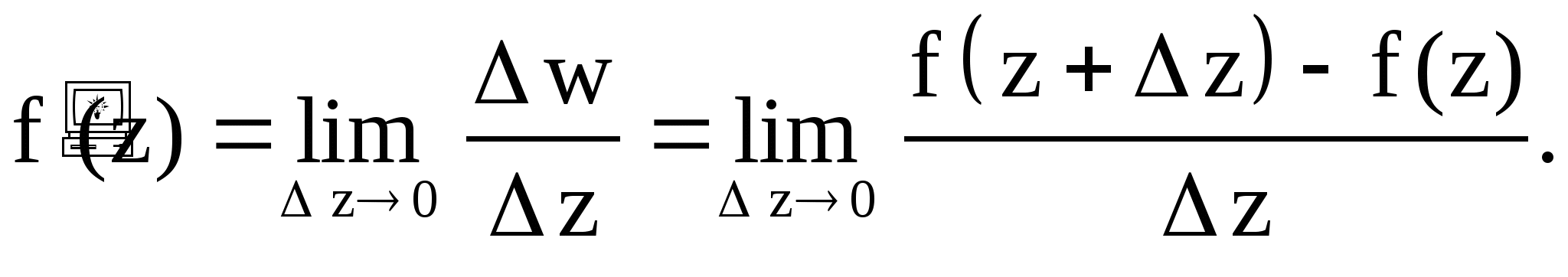
Функция, имеющая производную в точке ![]() , называется
дифференцируемой в этой точке.
, называется
дифференцируемой в этой точке.
Для дифференцируемости функции комплексного
переменного ![]()
![]() в данной точке
необходимо и достаточно, чтобы функции
в данной точке
необходимо и достаточно, чтобы функции ![]() и
и ![]() были дифференцируемы
в данной точке и удовлетворяли в этой точке условиям
Коши-Римана:
были дифференцируемы
в данной точке и удовлетворяли в этой точке условиям
Коши-Римана:
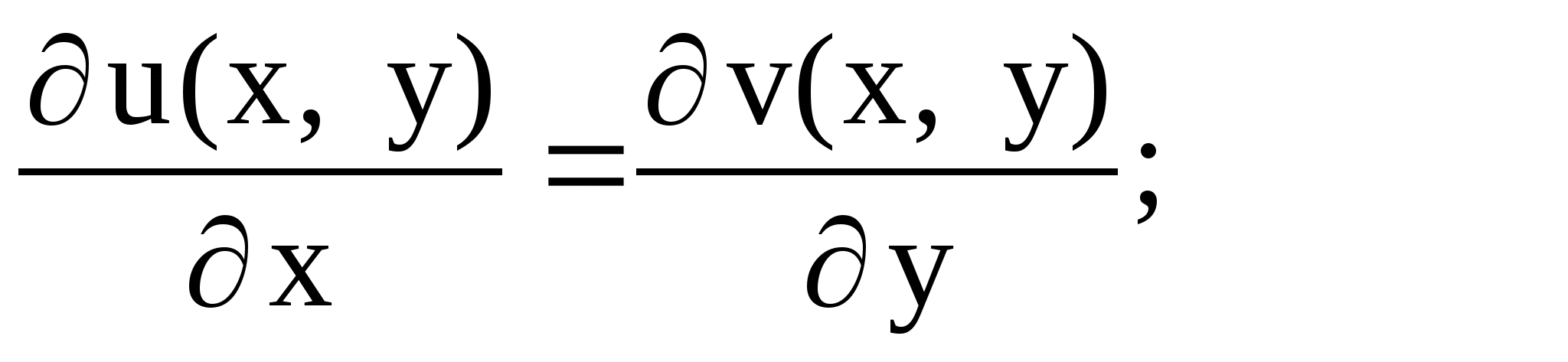
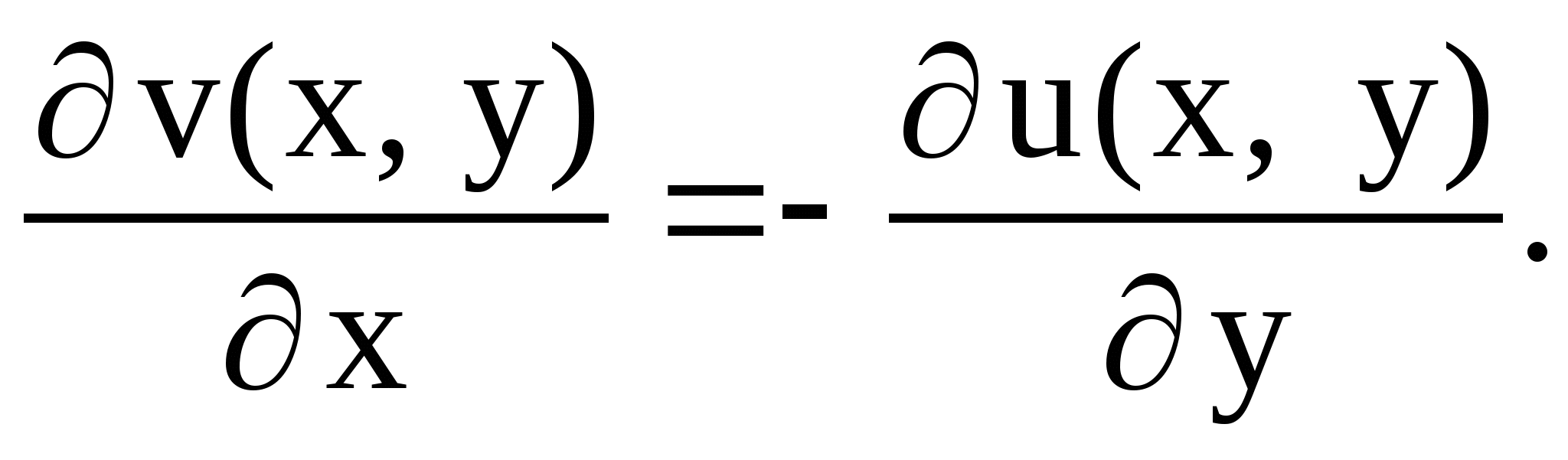
При этом 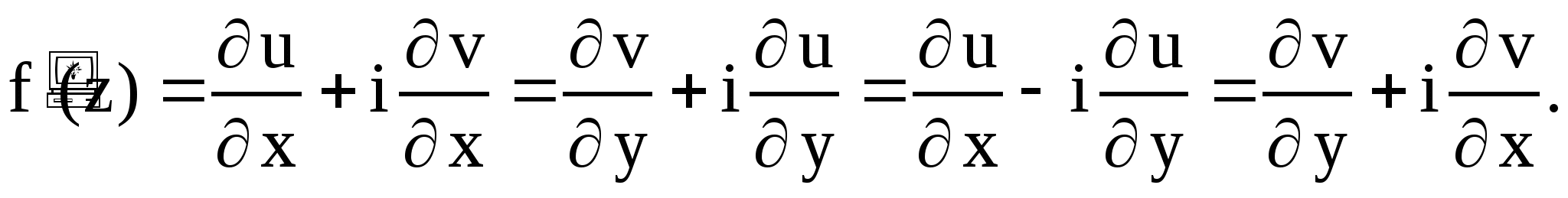
Так как основные свойства предельного перехода сохраняются, сохраняются основные правила дифференцирования.
Функция ![]() называется аналитической в области
называется аналитической в области ![]() , если она
дифференцируема в каждой точке области
, если она
дифференцируема в каждой точке области ![]() . Функция
. Функция ![]() называется
аналитической в точке
называется
аналитической в точке ![]() ,
,
![]() , если она аналитична
в некоторой ее окрестности.
, если она аналитична
в некоторой ее окрестности.
Элементарные функции в области определения аналитичны и для них справедливы основные формулы дифференцирования; для многозначных функций производные определяются для каждой ветви в отдельности.
Пример 5
Проверить выполнение условий Коши-Римана для
функции ![]() .
.
Решение
![]()
![]()
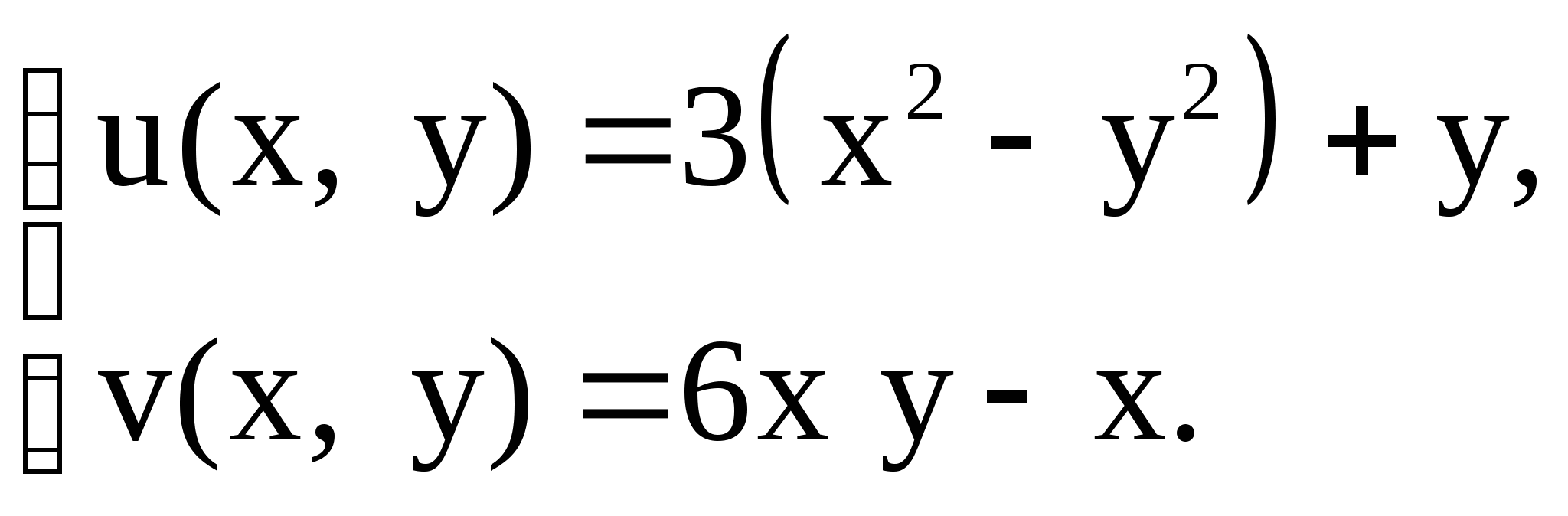
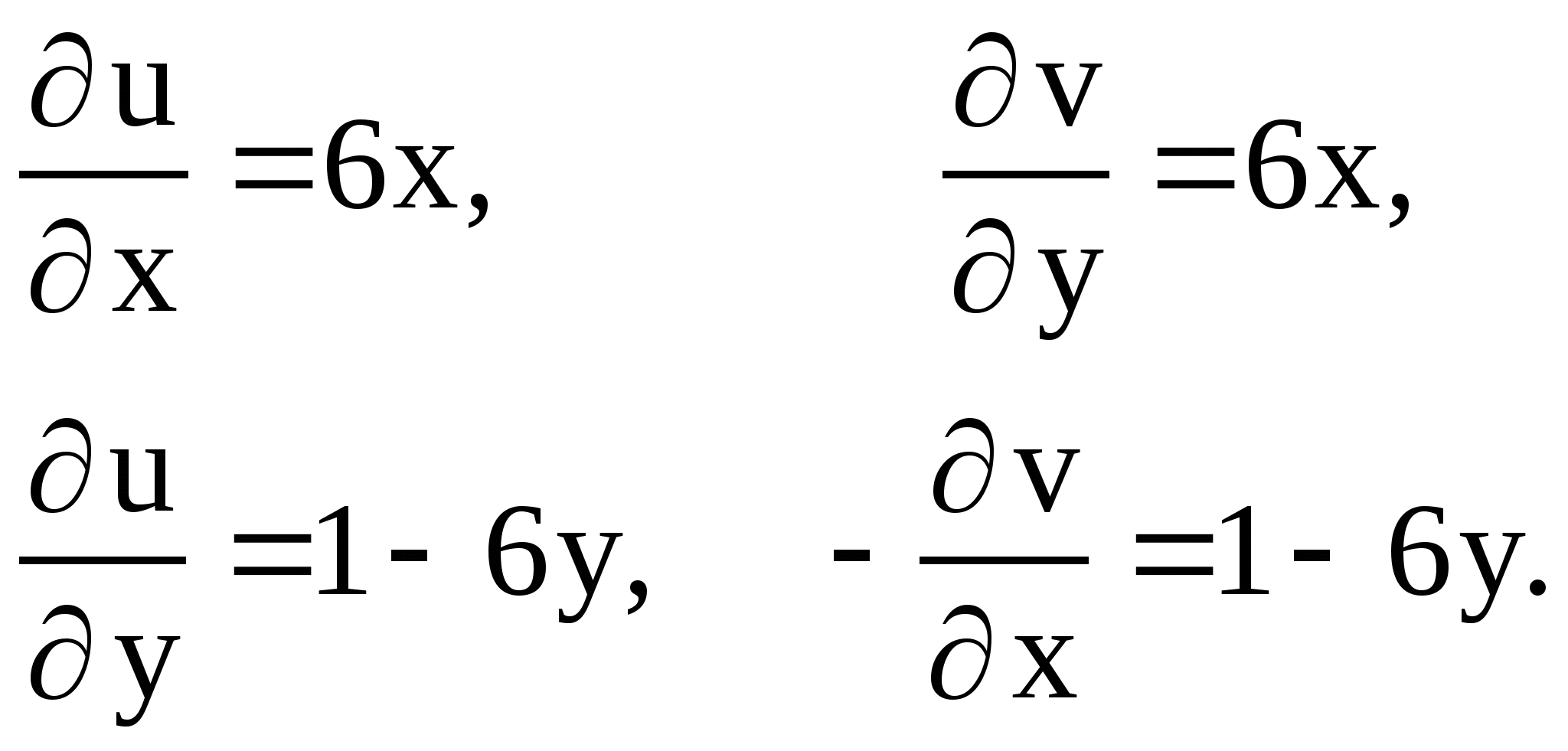
Условия Коши-Римана выполняются на всей плоскости, значит, функция дифференцируема на всей плоскости, и ее производная
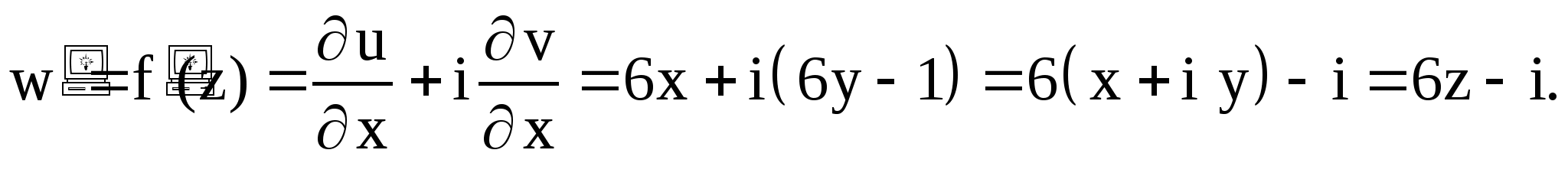
Пример 6
Показать, что при ![]() функция
функция ![]() не имеет производных.
не имеет производных.
Решение
![]()
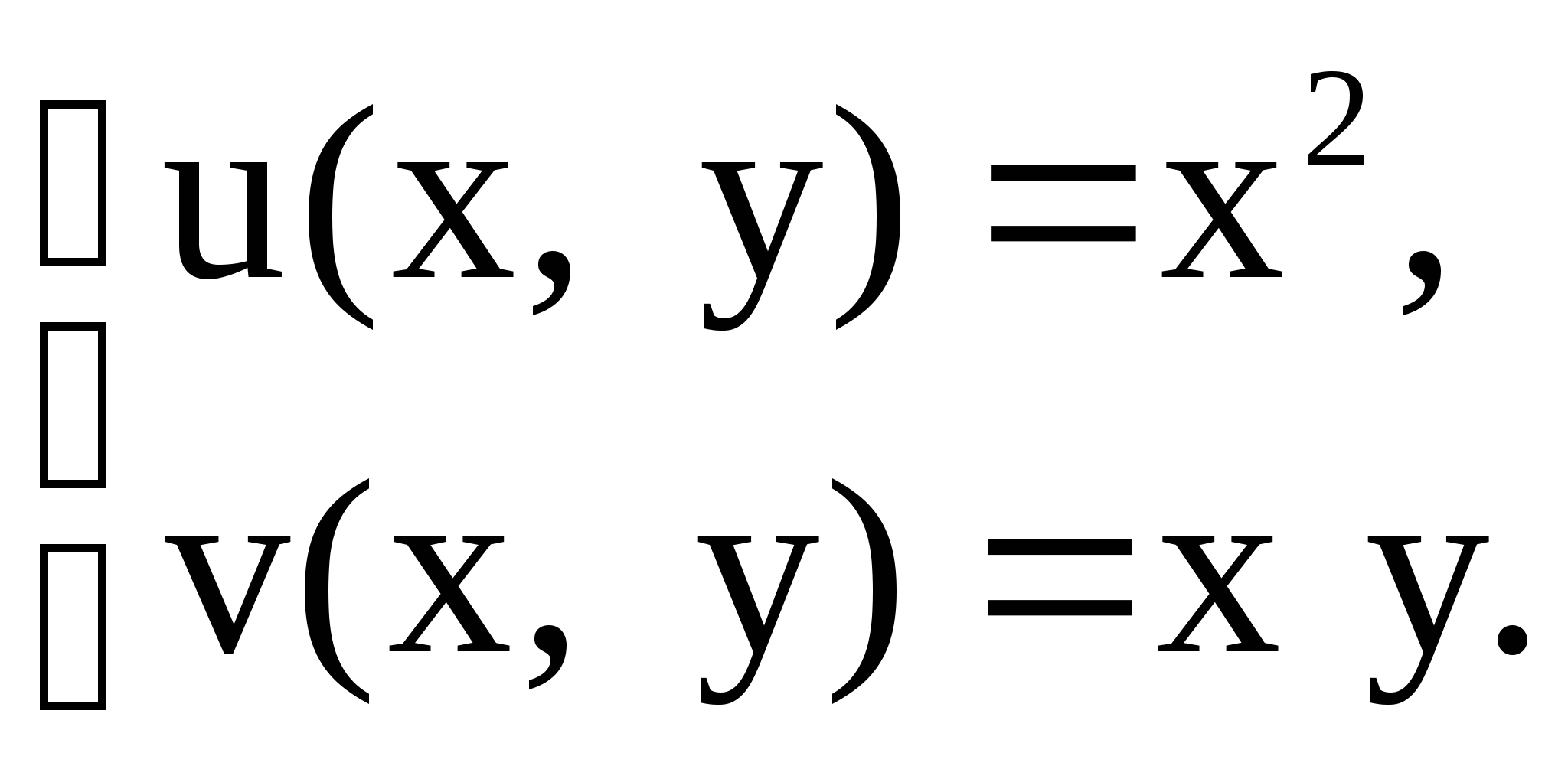
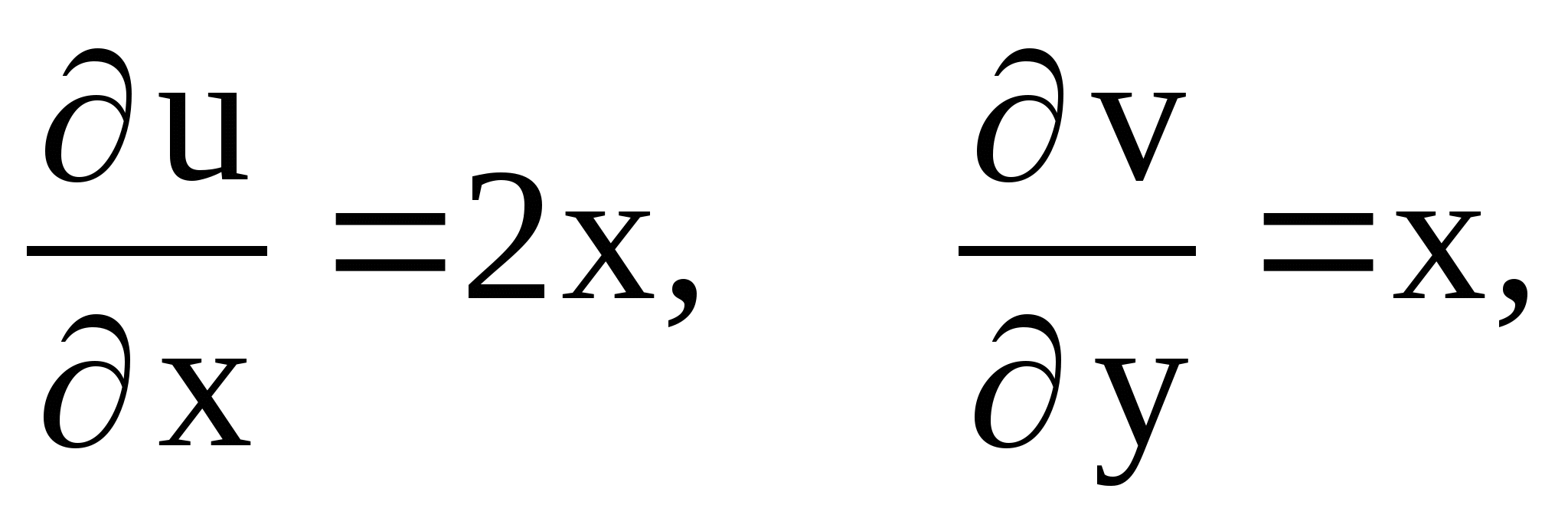 равны только при
равны только при
![]() ;
;
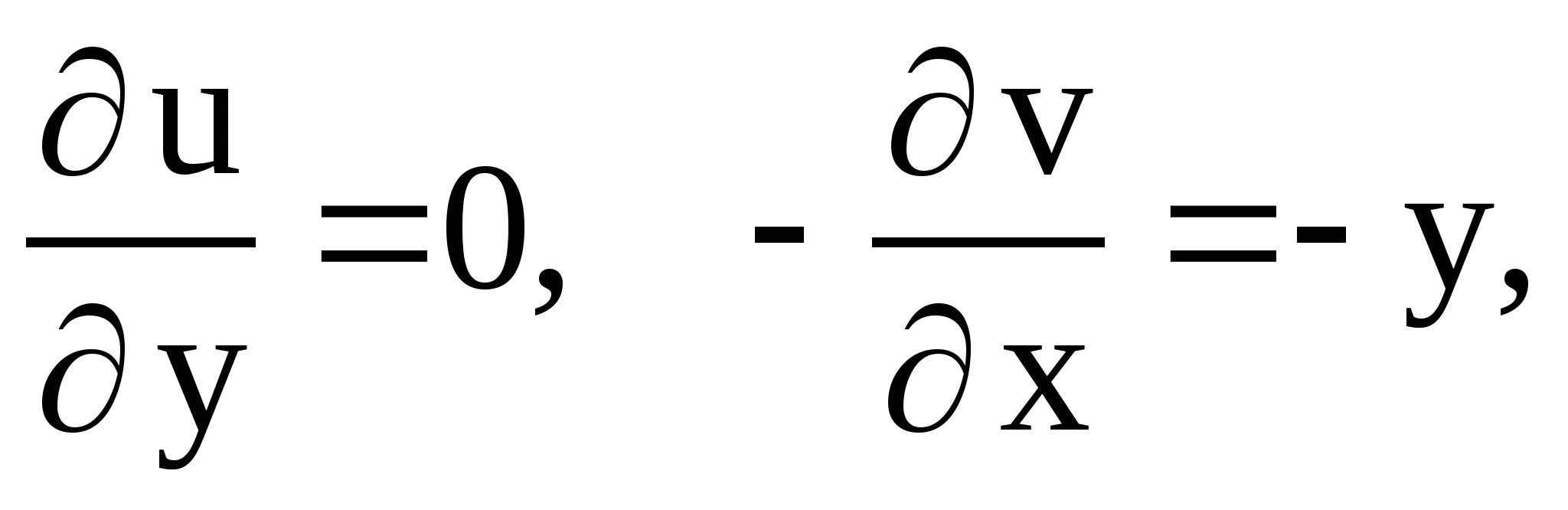 равны
только при
равны
только при ![]() .
.
Условия Коши-Римана не выполняются ни в одной
точке, кроме ![]() .
.
Замечание. ![]() в точке
в точке ![]() дифференцируема, но
не аналитична в ней, т. к. она не аналитична в окрестности этой
точки.
дифференцируема, но
не аналитична в ней, т. к. она не аналитична в окрестности этой
точки.
Функция двух действительных переменных ![]() , имеющая в области
, имеющая в области
![]() непрерывные частные
производные второго порядка и удовлетворяющая уравнению Лапласа
непрерывные частные
производные второго порядка и удовлетворяющая уравнению Лапласа
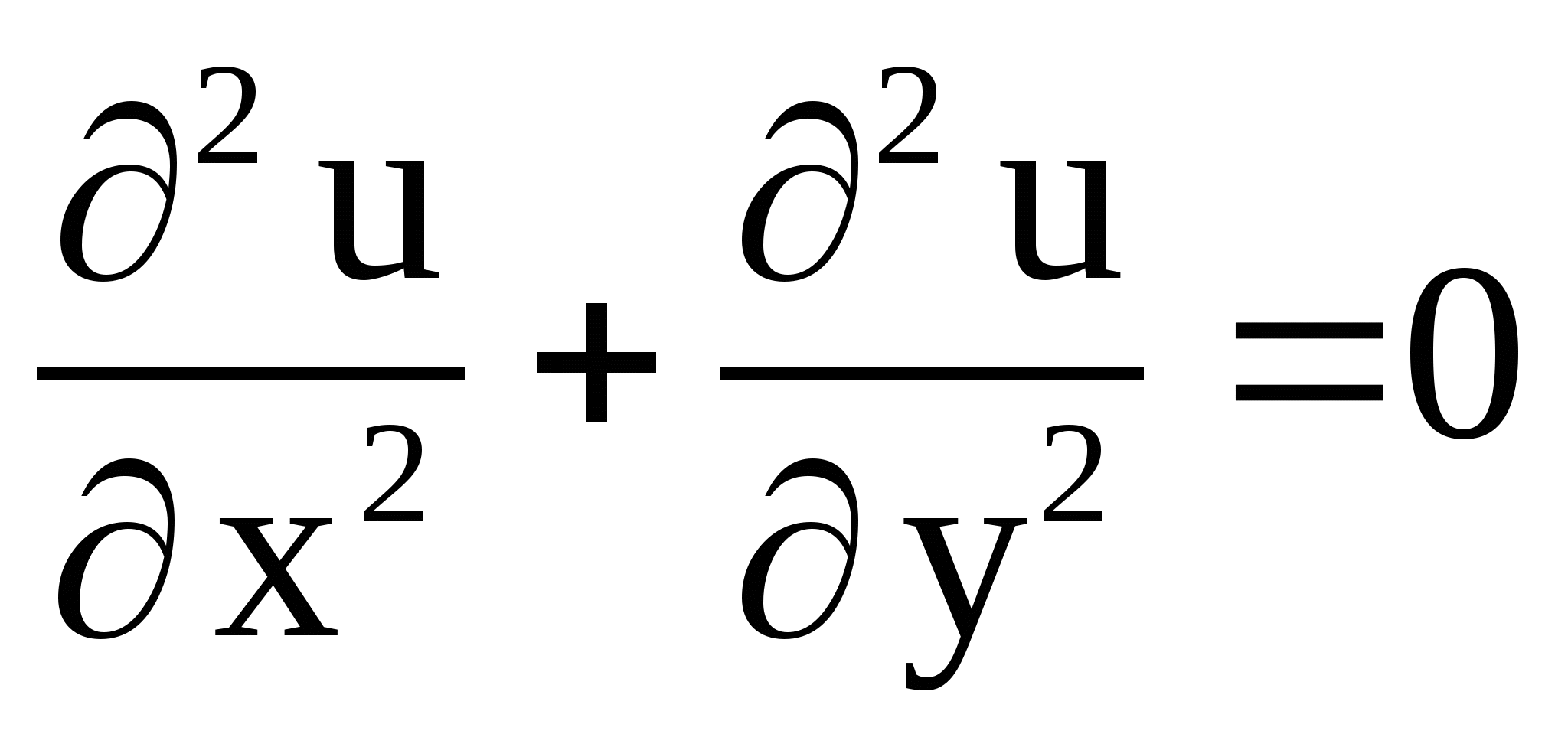 , называется
гармонической в области
, называется
гармонической в области ![]() .
.
Действительная и мнимая части аналитической в
односвязной области ![]() функции
функции ![]() являются
гармоническими функциями в области
являются
гармоническими функциями в области ![]() . Для всякой
гармонической в односвязной области функции
. Для всякой
гармонической в односвязной области функции ![]() существует функция
существует функция
![]() , аналитичная в
области
, аналитичная в
области ![]() . Ее мнимая часть
. Ее мнимая часть
![]() называется функцией,
гармонически сопряженной с функцией
называется функцией,
гармонически сопряженной с функцией ![]() . Аналогично для
всякой гармонической в односвязной области
. Аналогично для
всякой гармонической в односвязной области ![]() функции
функции ![]() существует функция
существует функция
![]() , аналитическая в
области
, аналитическая в
области ![]() .
.
Пример 7
Найти аналитическую функцию ![]() , если
, если
![]()
Решение. Функция ![]() является
гармонической. Действительно,
является
гармонической. Действительно,
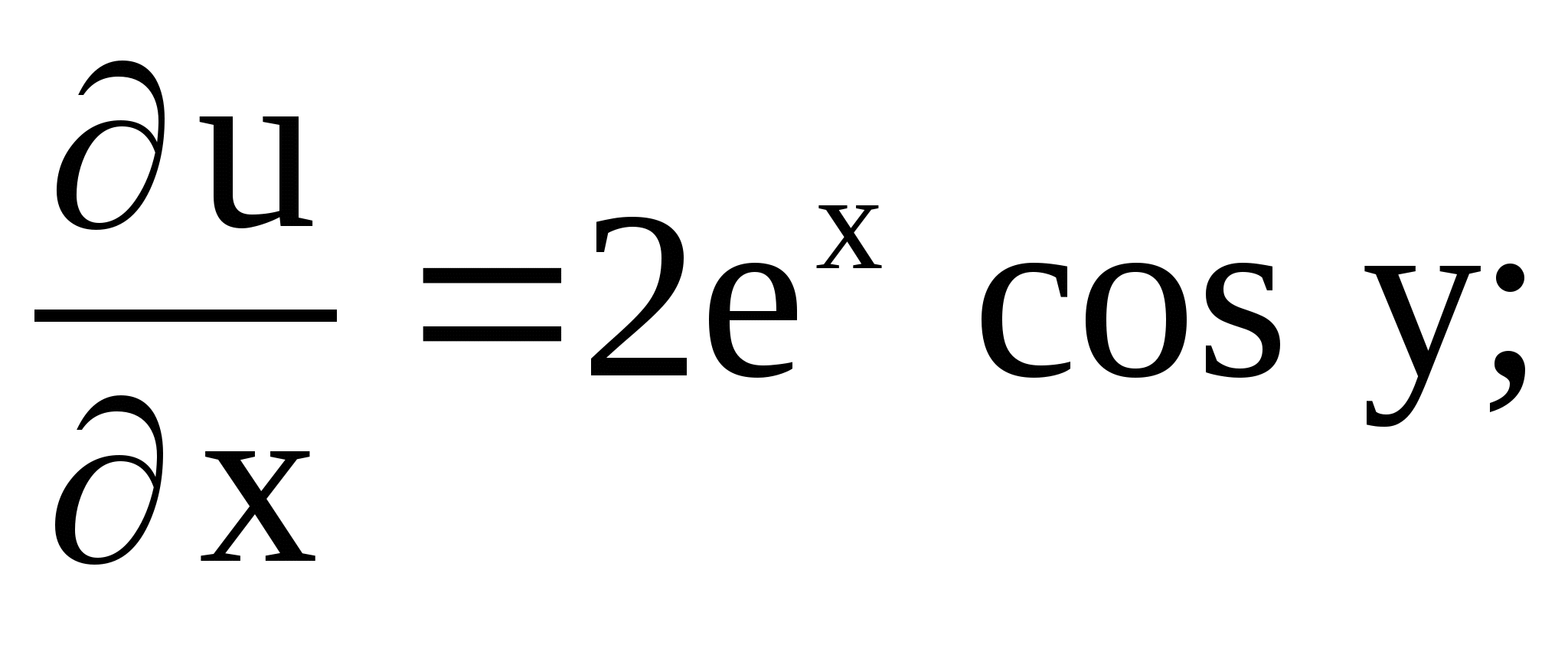
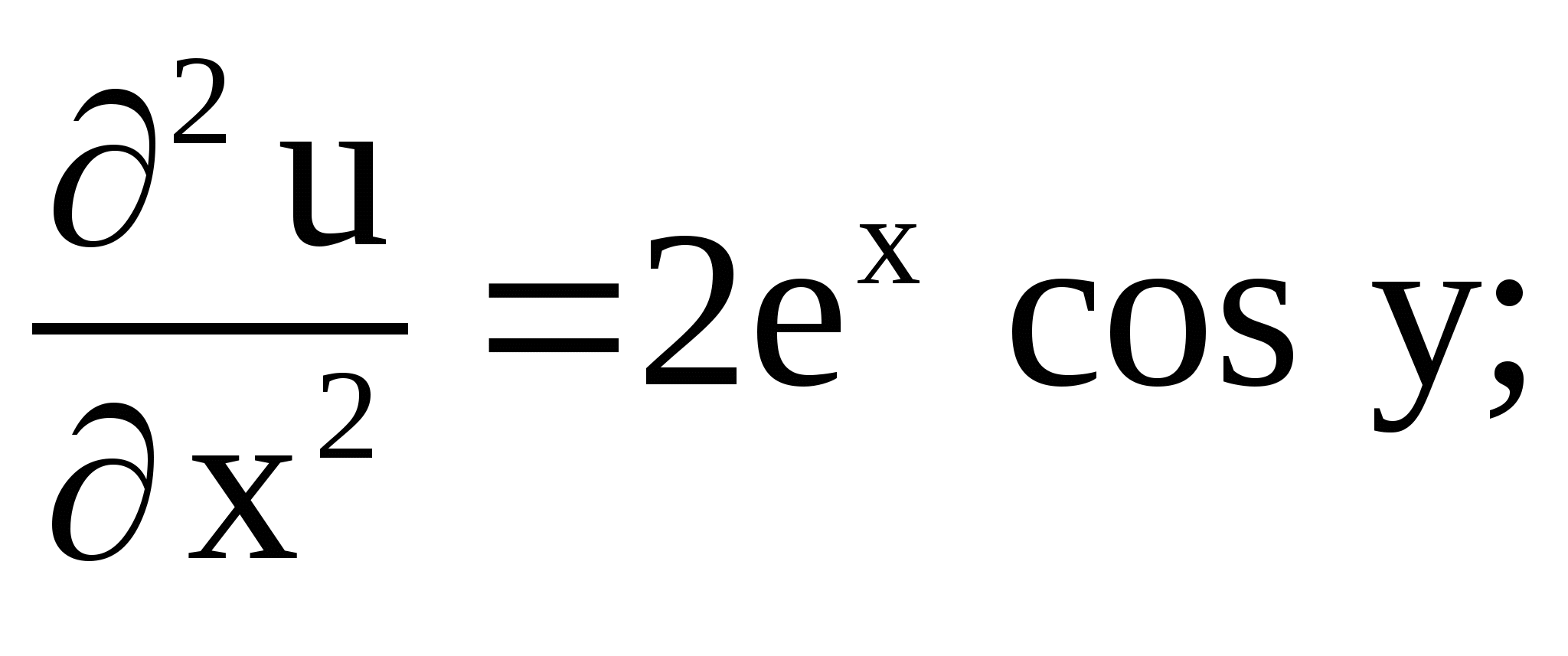
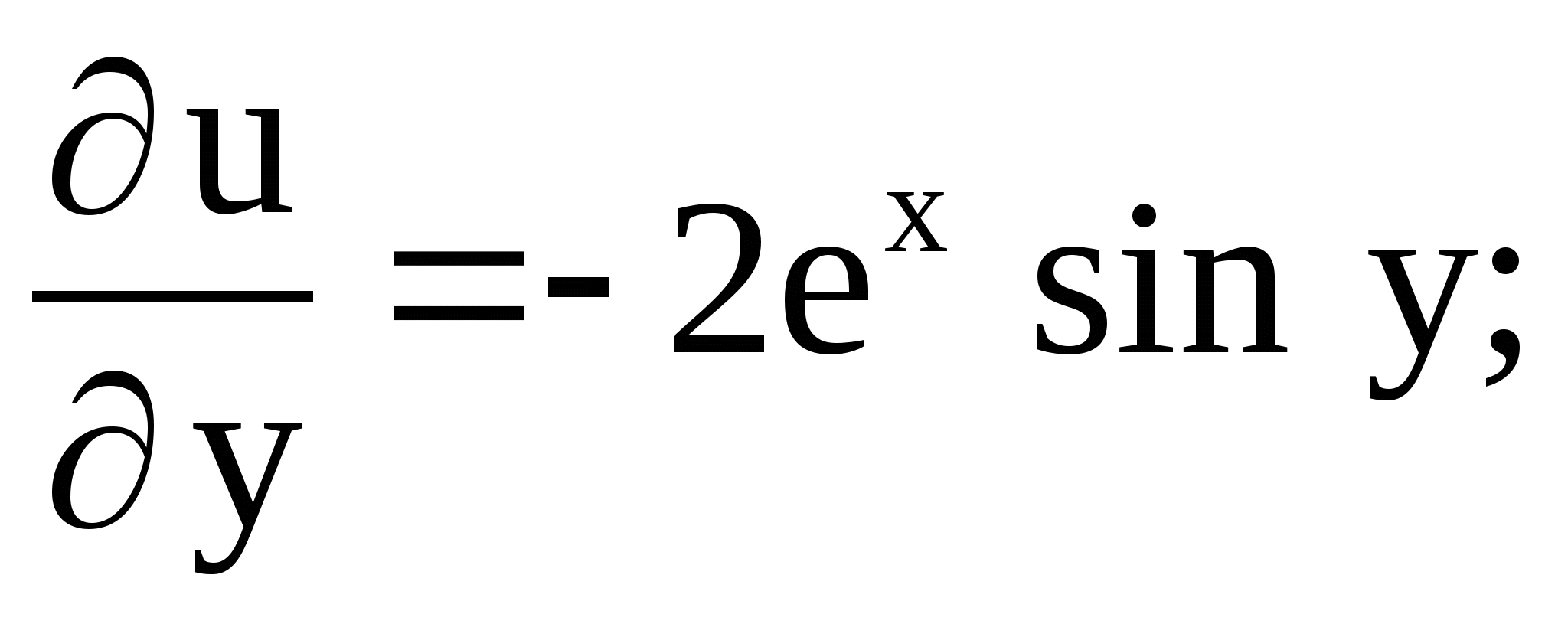
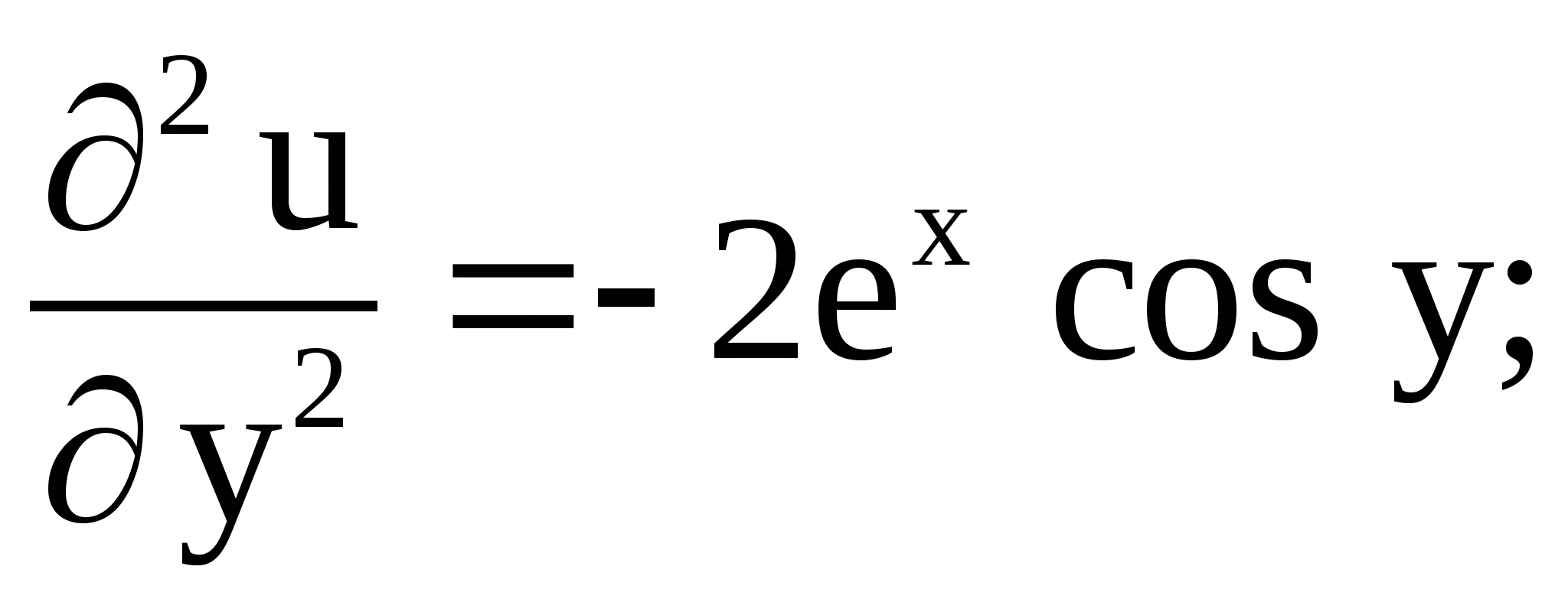
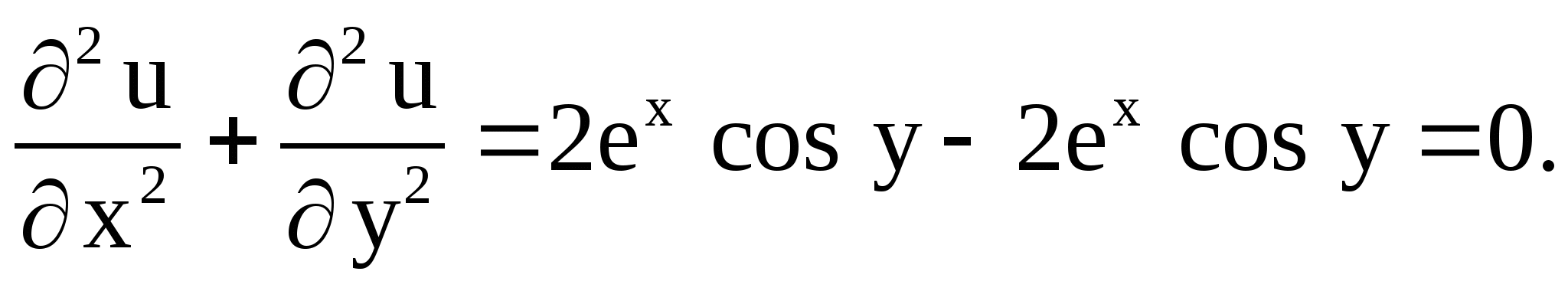
Из условий Коши-Римана следует, что
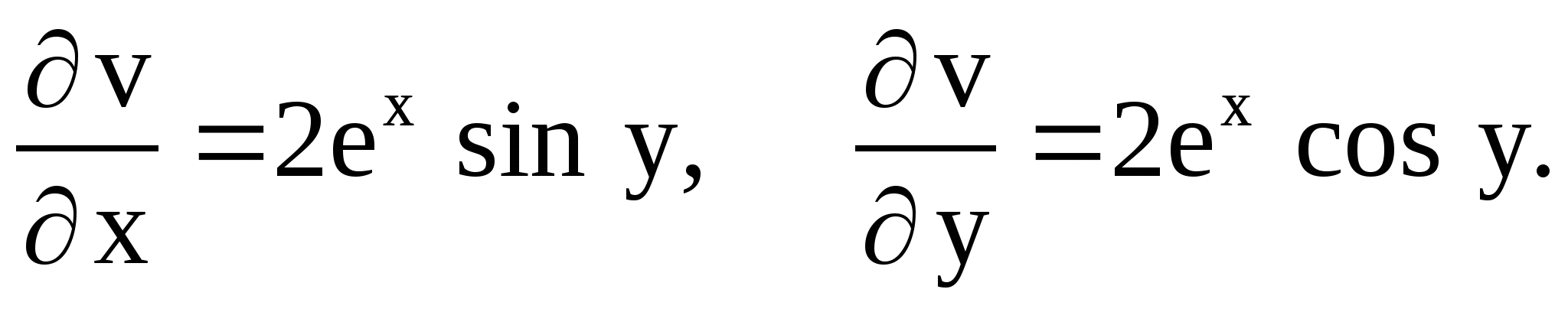
Тогда 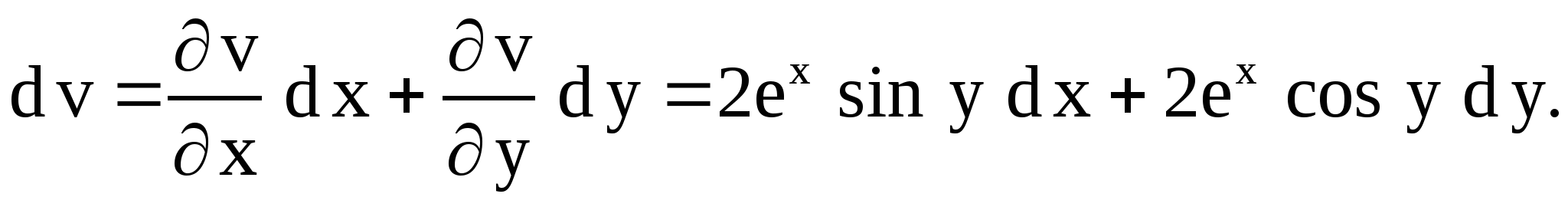
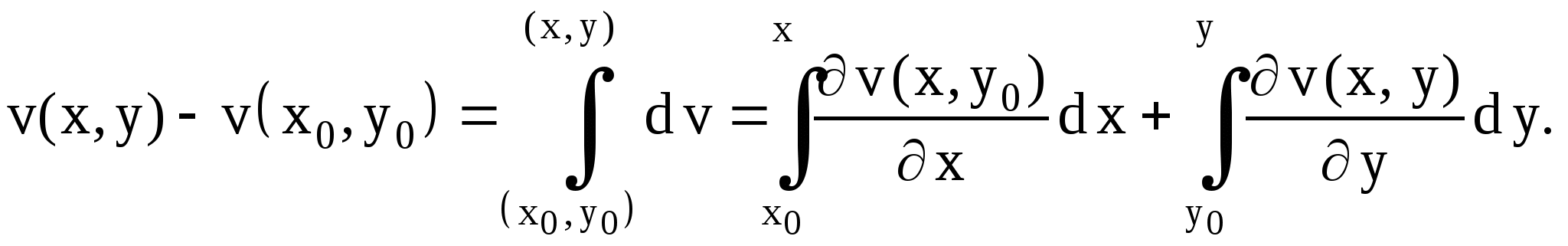
Так как ![]()
![]()
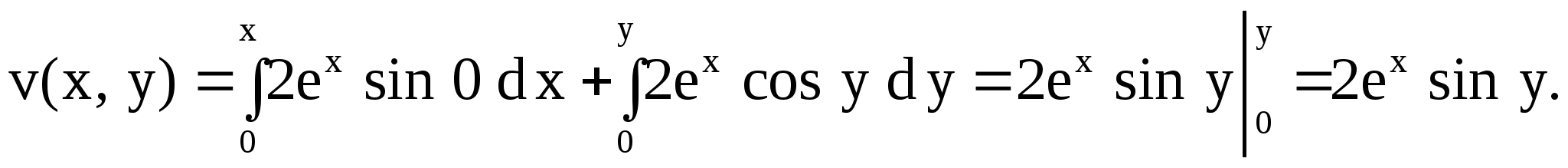
![]()
Если аналитическая в области ![]() функция
функция ![]() отображает эту
область на область
отображает эту
область на область ![]() плоскости
плоскости ![]() , причем всюду в
области
, причем всюду в
области ![]() :
: ![]() , то
, то ![]() равен коэффициенту
растяжения, происходящему при этом отображении в точке
равен коэффициенту
растяжения, происходящему при этом отображении в точке
![]() , а
, а ![]() равен углу
поворота каждой из гладких линий, проходящих через точку
равен углу
поворота каждой из гладких линий, проходящих через точку
![]() , при том же
отображении.
, при том же
отображении.
Пример 8. Найти коэффициент растяжения и
угол поворота при отображении ![]() в точке
в точке ![]() .
.
Решение. Коэффициент растяжения
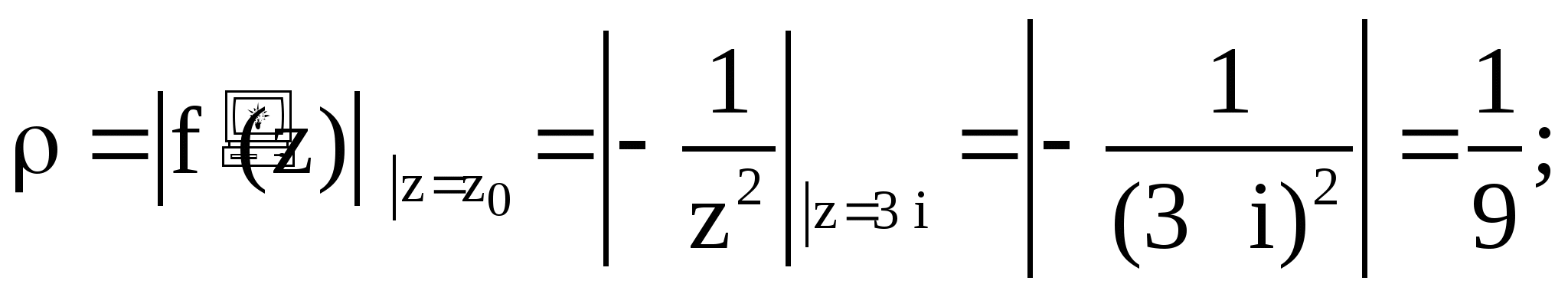
угол поворота 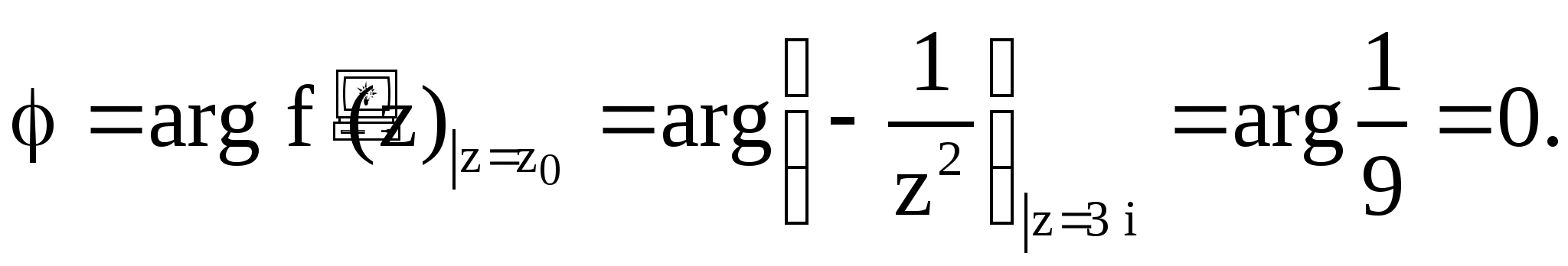
§2.2 Задачи
2.1. Проверить выполнение условий
Коши-Римана для следующих функций:в) ![]()
2.2. Показать, что при ![]() функция
функция ![]() не имеет производных.
не имеет производных.
2.3. Будет ли дифференцируемой функция
![]()
2.4. Найти область, в которой функция
![]() будет аналитической.
будет аналитической.
2.5. Определить вещественные функции
![]() и
и ![]() так, чтобы функция
так, чтобы функция
![]() была
дифференцируемой.
была
дифференцируемой.
2.6. Найти аналитическую функцию
![]() , если
, если
а) ![]()
б) 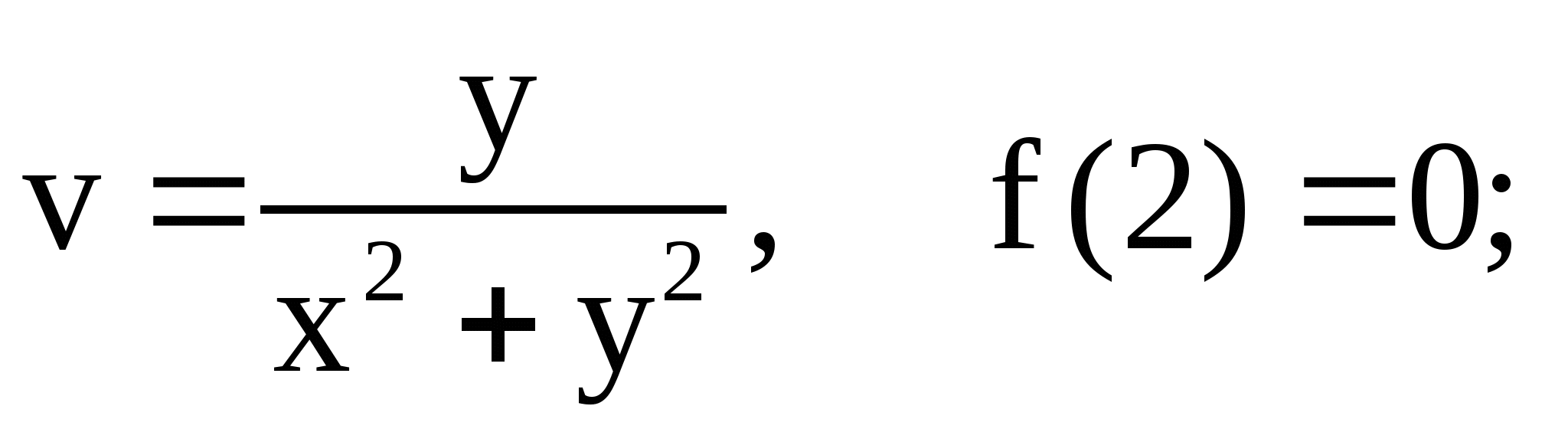
в) ![]()
2.7. Найти коэффициент растяжения и угол поворота при отображении
![]() в
точке
в
точке ![]() : а)
: а) ![]() б)
б) ![]()
2.8. Найти линии равного растяжения и
линии равного угла поворота для отображений: а) ![]() б)
б) ![]() .
.
2.9. Выяснить геометрический смысл
производной линейной функции ![]() .
При отображениях
.
При отображениях ![]() и
и ![]() найти образ квадрата:
найти образ квадрата:
![]()
§2.3 Задачи для самостоятельного решения
2.10. Будет ли дифференцируемой функция
![]()
2.11. Показать, что функция ![]() дифференцируема и
найти ее производную.
дифференцируема и
найти ее производную.
2.12. При каком значении ![]() функция
функция ![]() дифференцируема?
дифференцируема?
2.13. При каком значении ![]() функция
функция ![]() дифференцируема?
дифференцируема?
2.14. Найти аналитическую функцию
![]() , если
, если
а) ![]() б)
б)
![]() в)
в) ![]() .
.
2.15. Найти коэффициент растяжения и угол
поворота при отображении ![]() :
:
а) ![]() в
точках
в
точках ![]()
б) ![]() в
точках
в
точках ![]() .
.
§3.1 Ответы на задачи для самостоятельного решения
1.1. а) ![]() б)
б) ![]()
в) 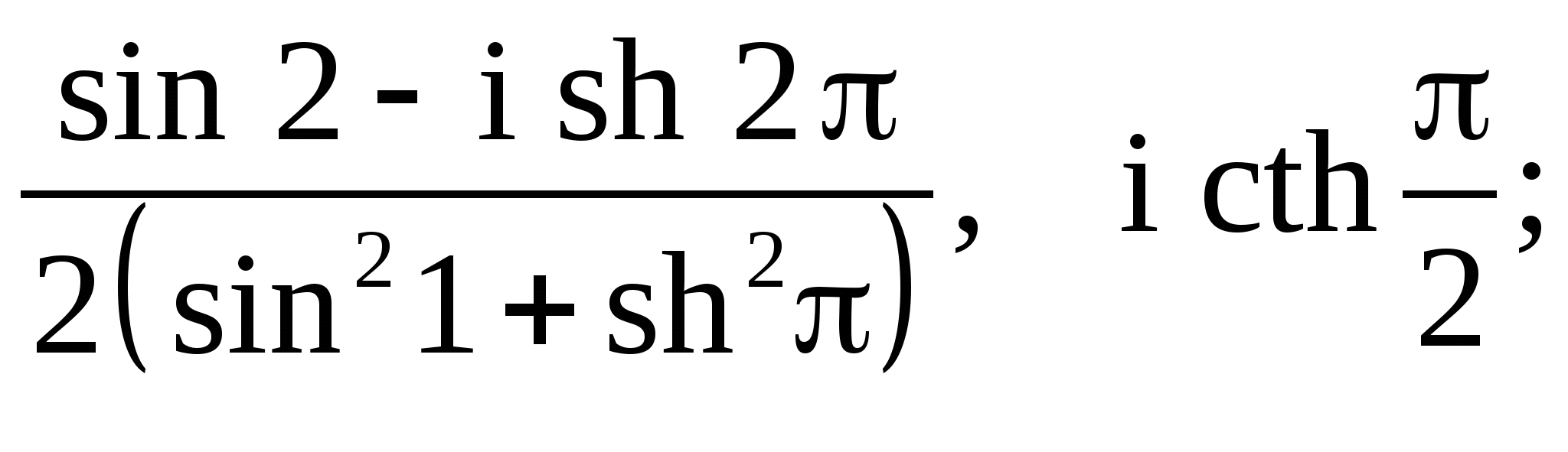 г)
г) ![]()
д) 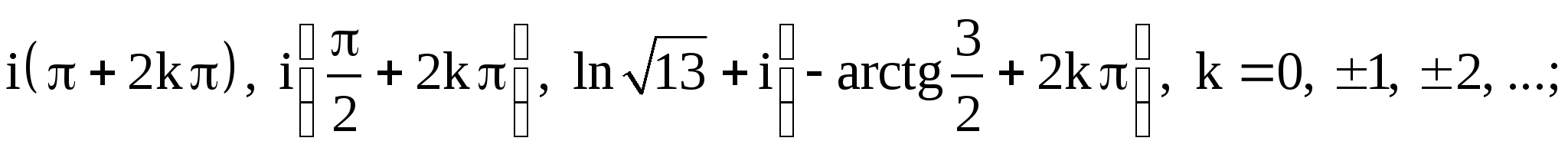
е) ![]()
![]()
1.2. 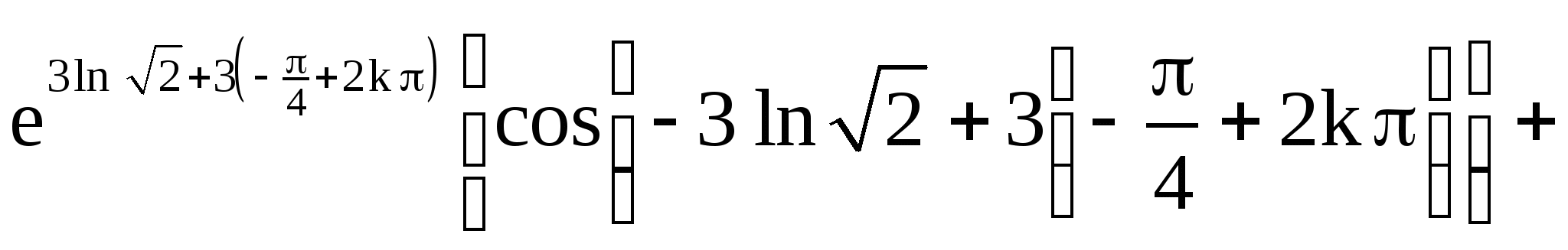
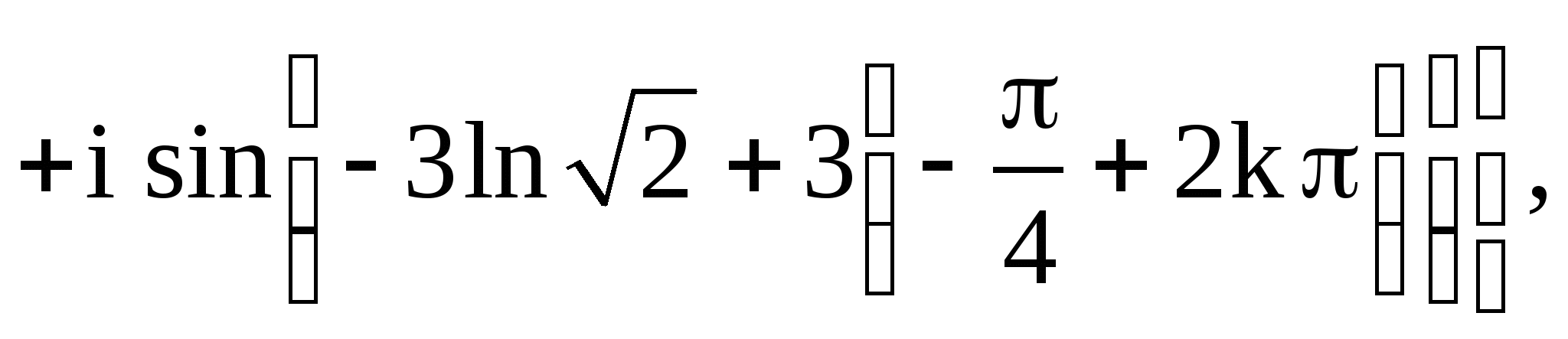
![]()
1.3. ![]()
1.4. а) ![]()
б) 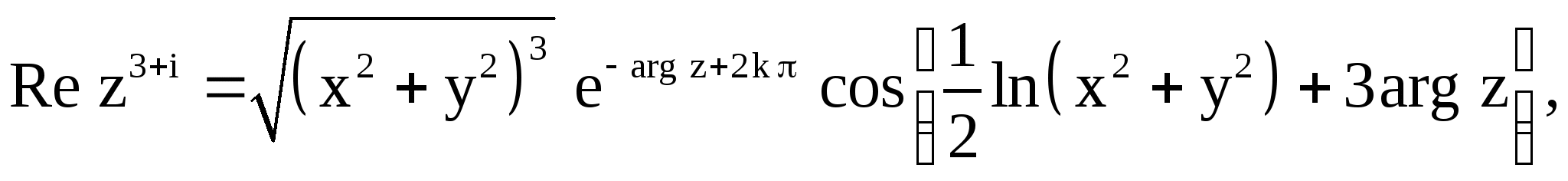
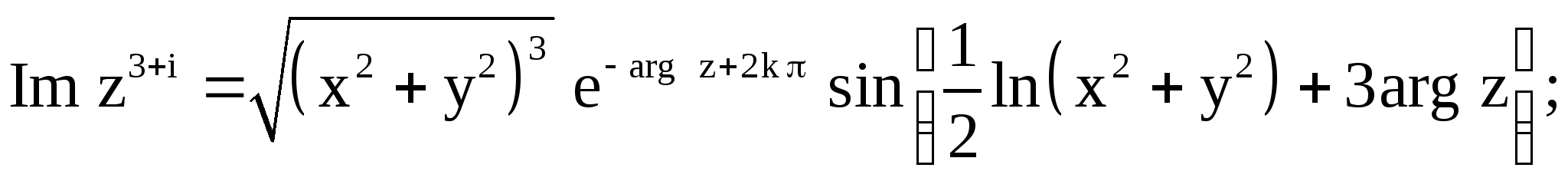
в) ![]()
![]()
1.5. ![]()
1.8. ![]()
1.9. Образом являются два семейства парабол с общим фокусом в начале координат и с осями, совпадающими с действительной осью.
1.10. 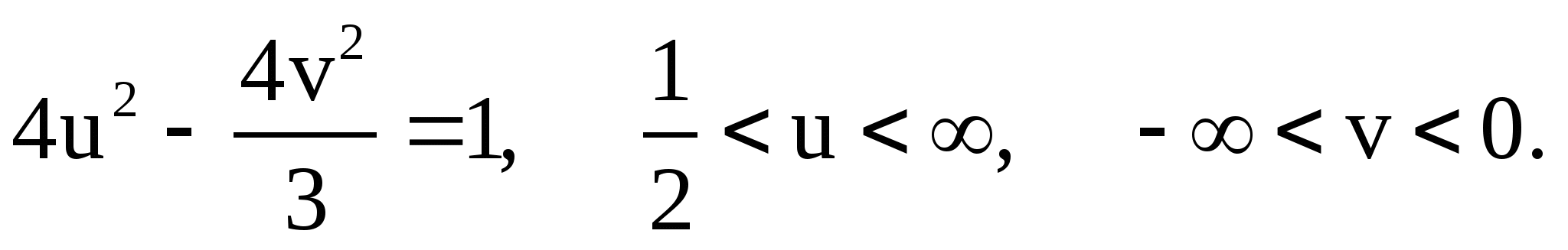
1.11. а) ![]() б)
б) ![]()
в) 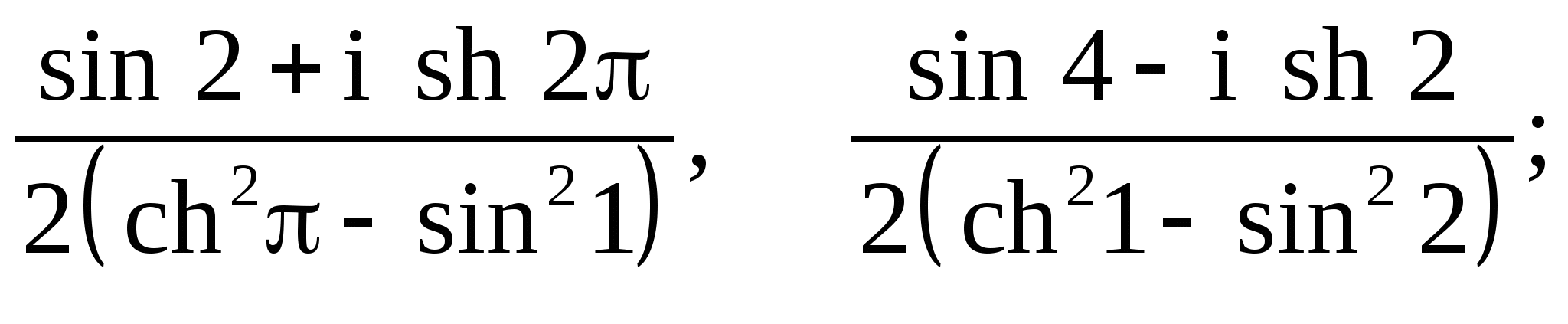
г) ![]()
д) 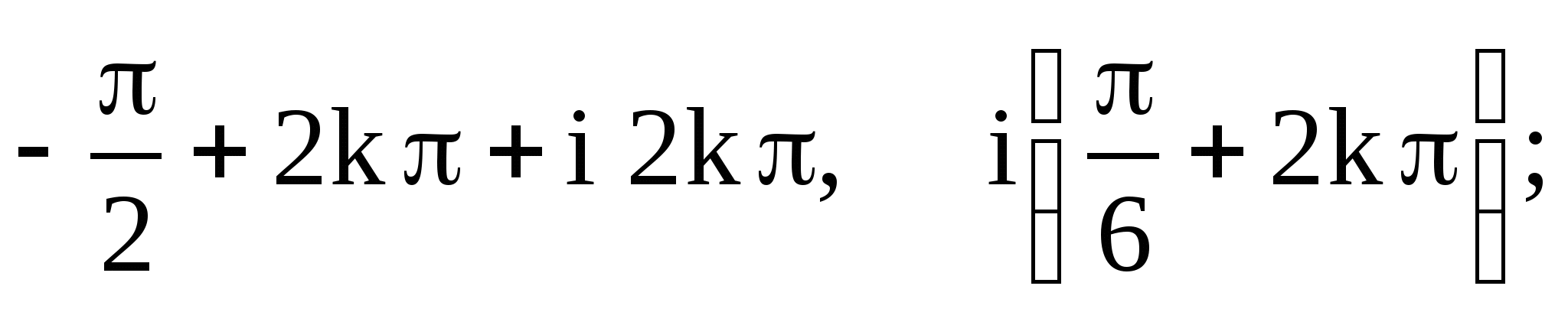 е)
е) ![]()
1.12. ![]()
1.13. ![]()
1.14. а) ![]()
б) ![]()
в) ![]()
1.16. ![]()
1.17. 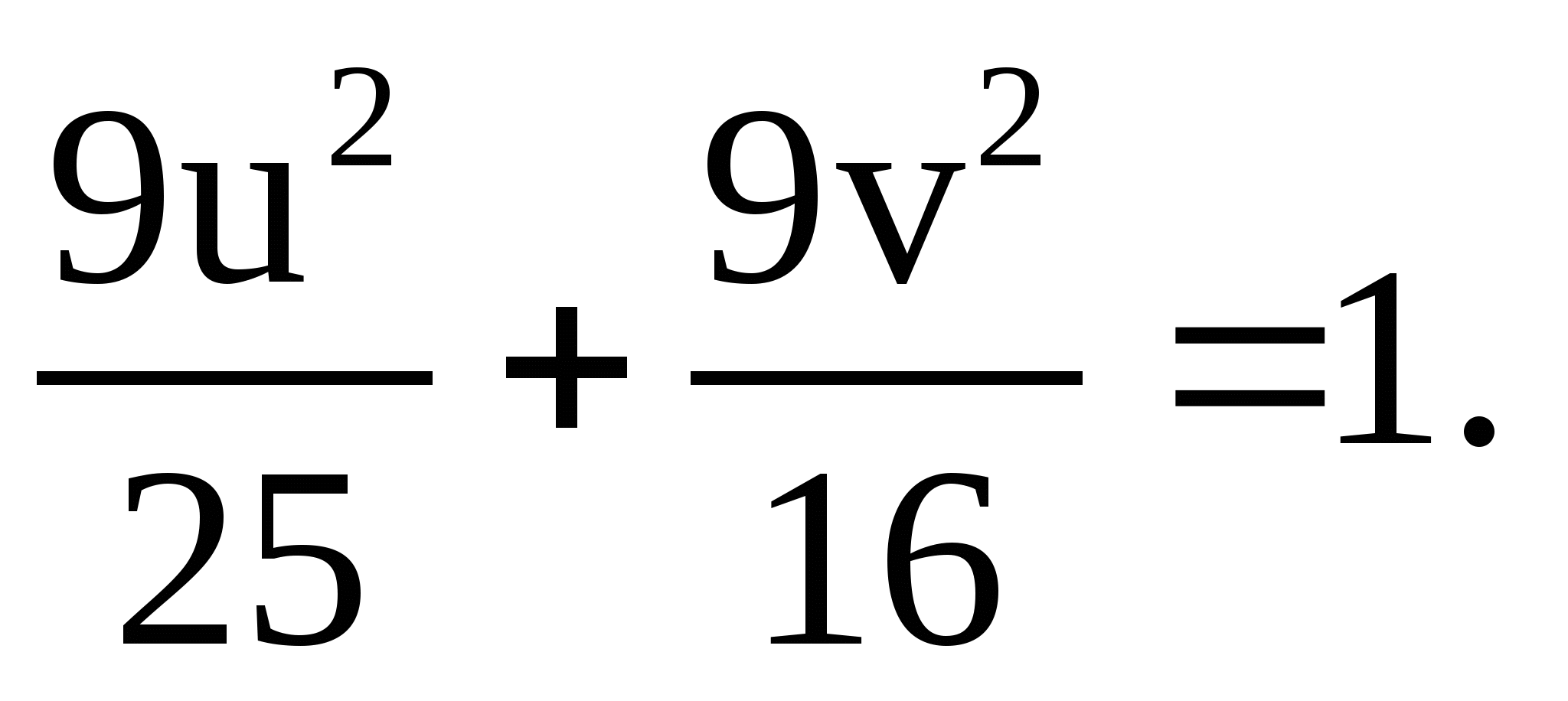
1.18. Прообразом являются два семейства
равнобочных гипербол. У одного семейства асимптоты есть биссектрисы
координатных углов, а у другого асимптотами служат оси ![]() и
и ![]() .
.
2.3. Нет.
2.4. Функция аналитическая при ![]()
![]()
и при ![]()
2.5. ![]()
2.6. а) ![]()
б) ![]()
в) ![]()
2.7. а) ![]()
б) ![]()
2.8. а)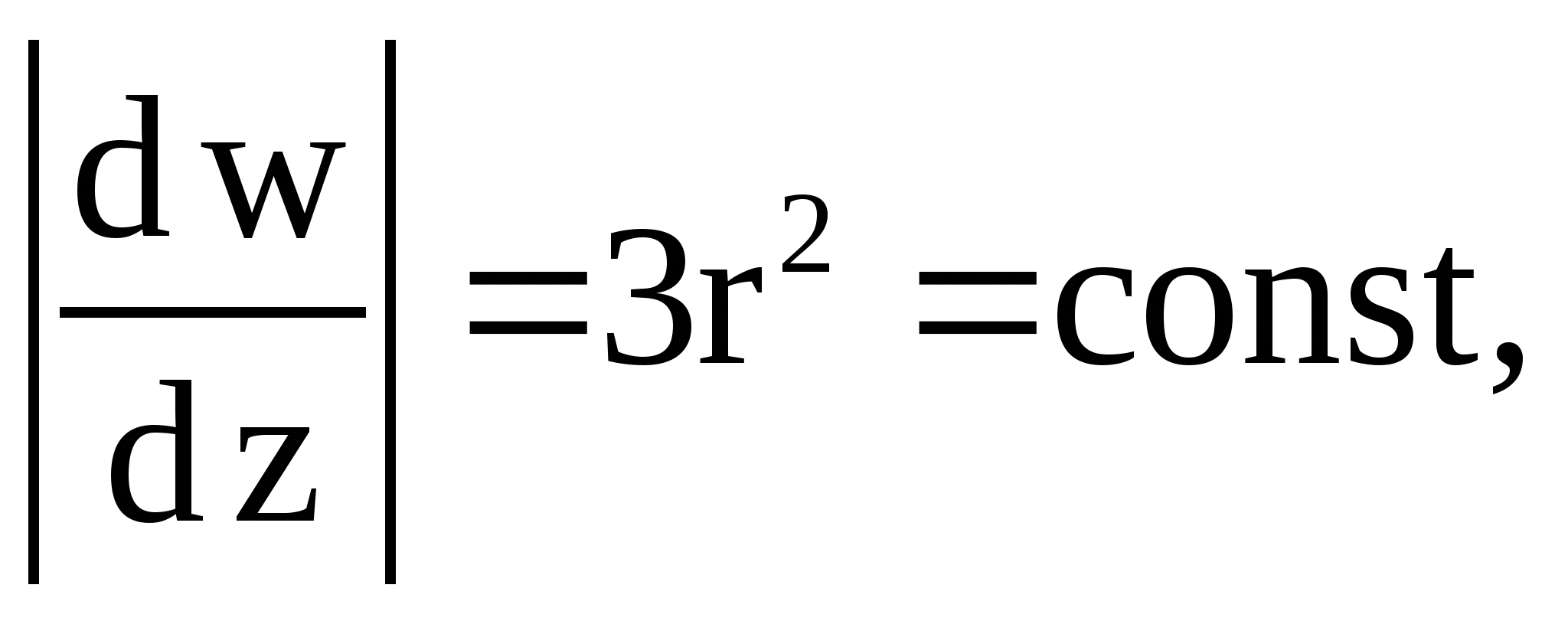
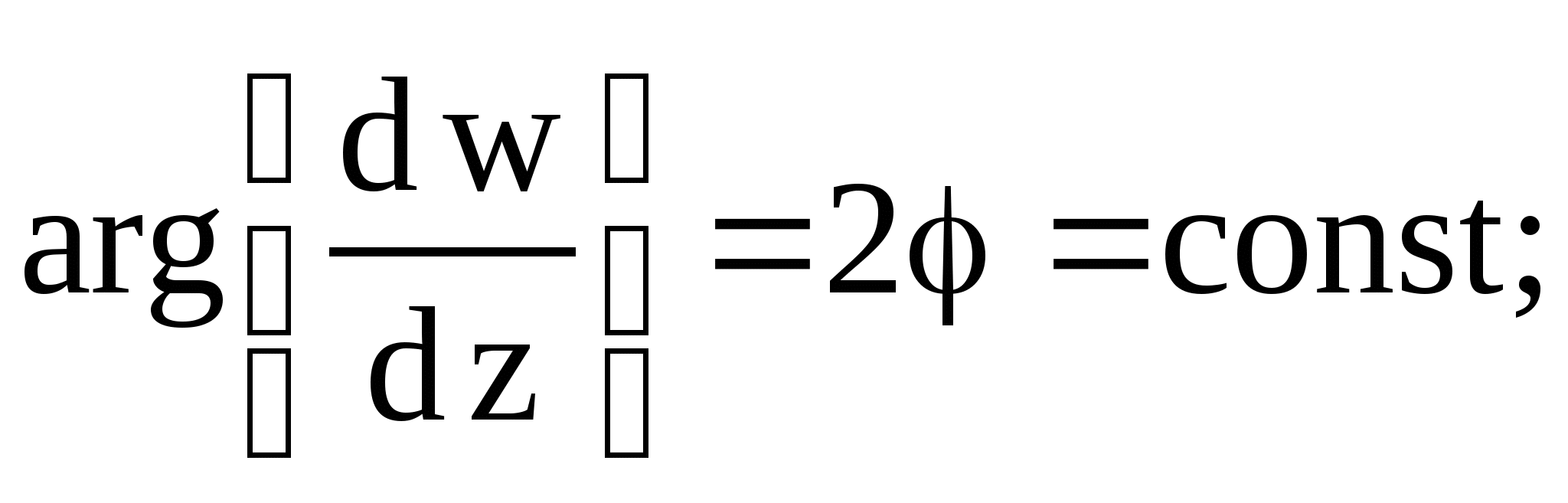
б) 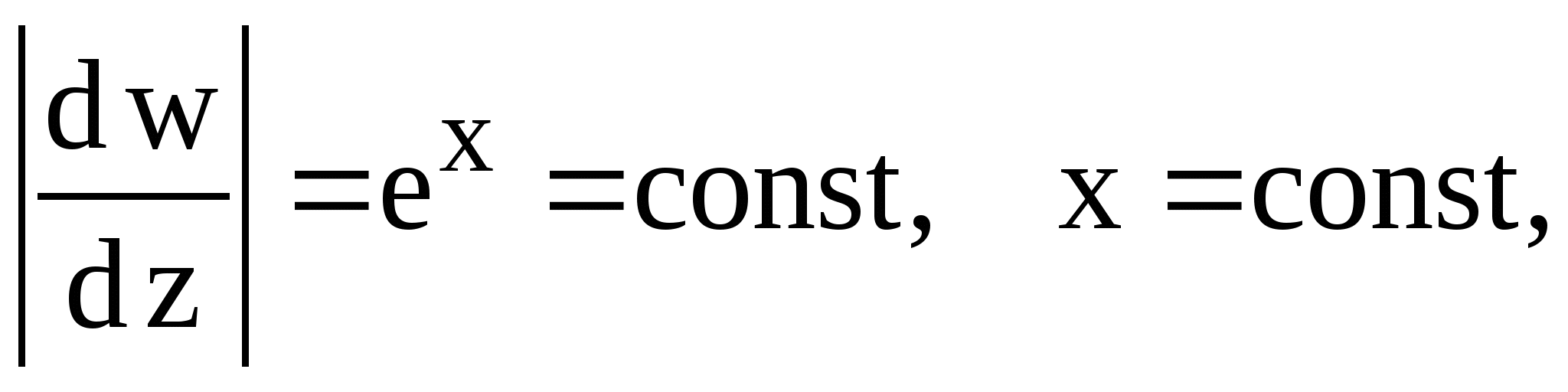
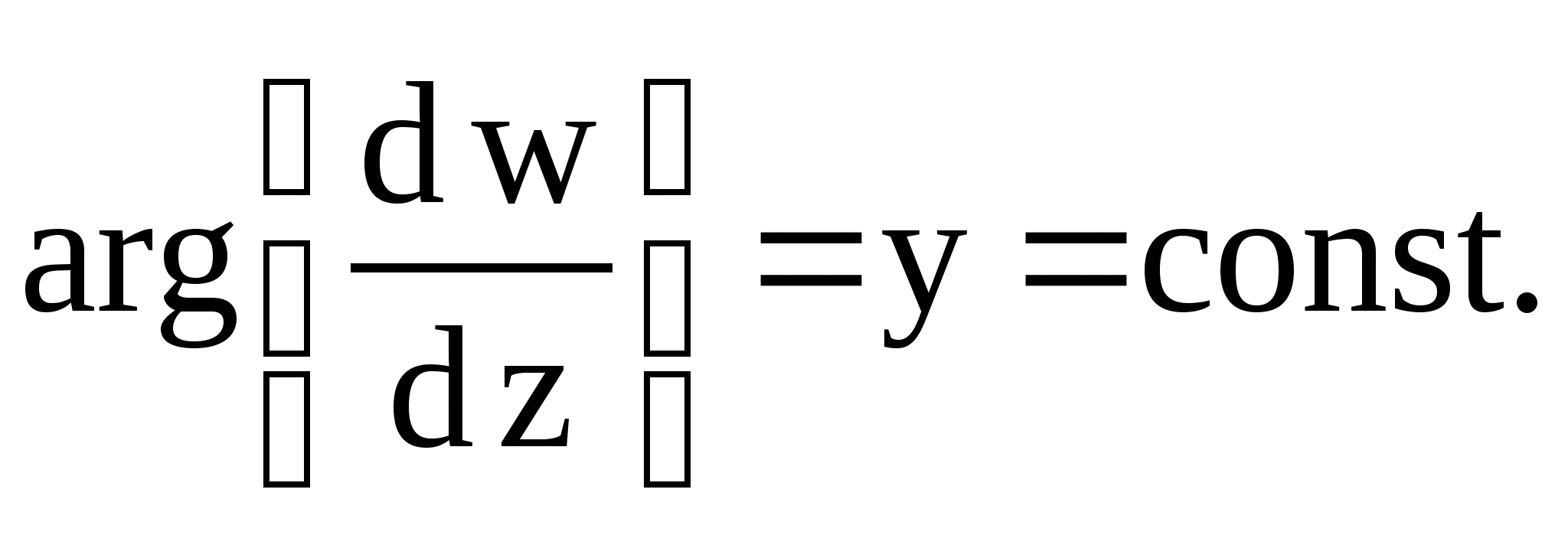
2.9. ![]()
![]()
2.10. Нет.
2.11. ![]()
2.12. ![]()
2.13. ![]()
2.14. а) ![]()
б) ![]()
в) ![]()
2.15. а) ![]()
б) ![]()
§4.1 Задачи контрольной работы
Задача 1
Выполнить указанные действия:1.
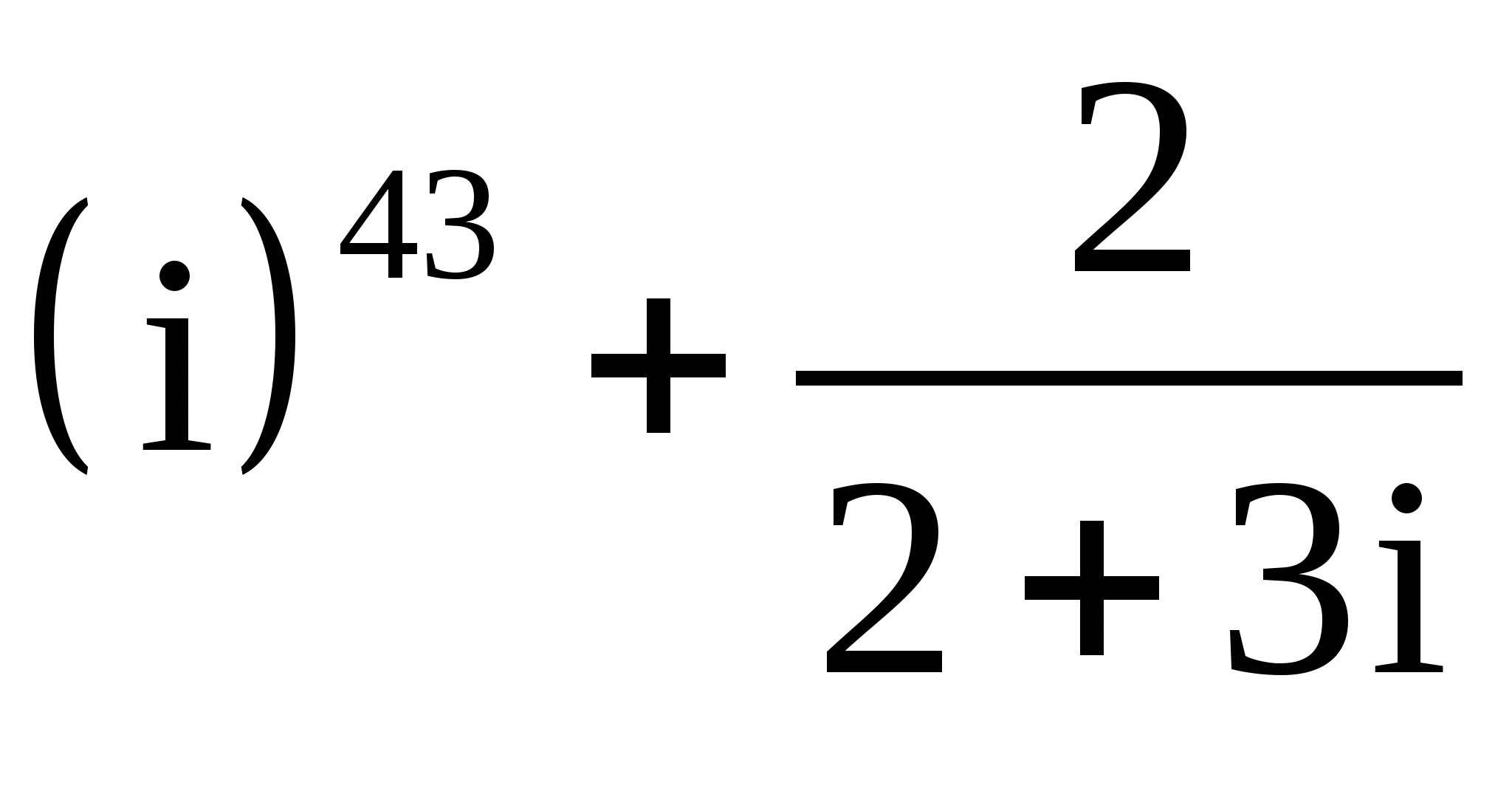 ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
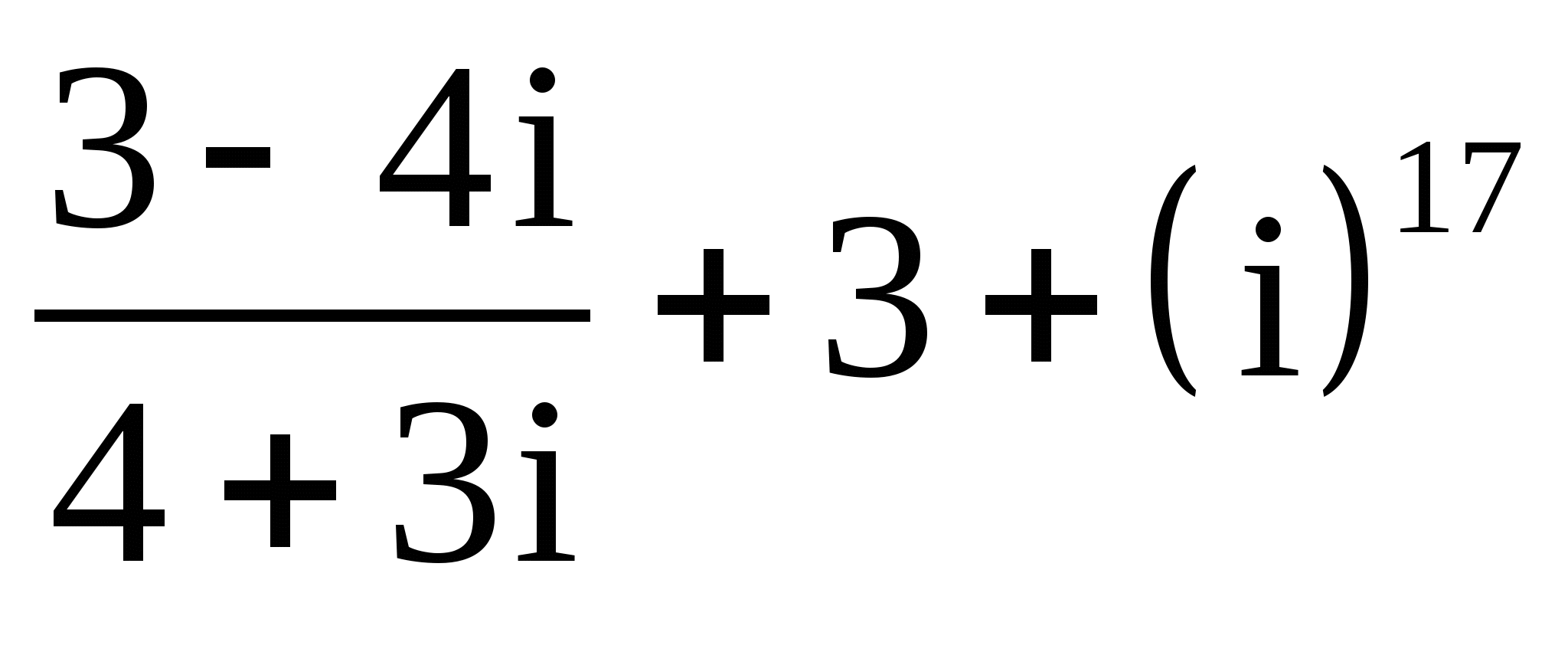 ;
;
5.
![]() ;
;
6.
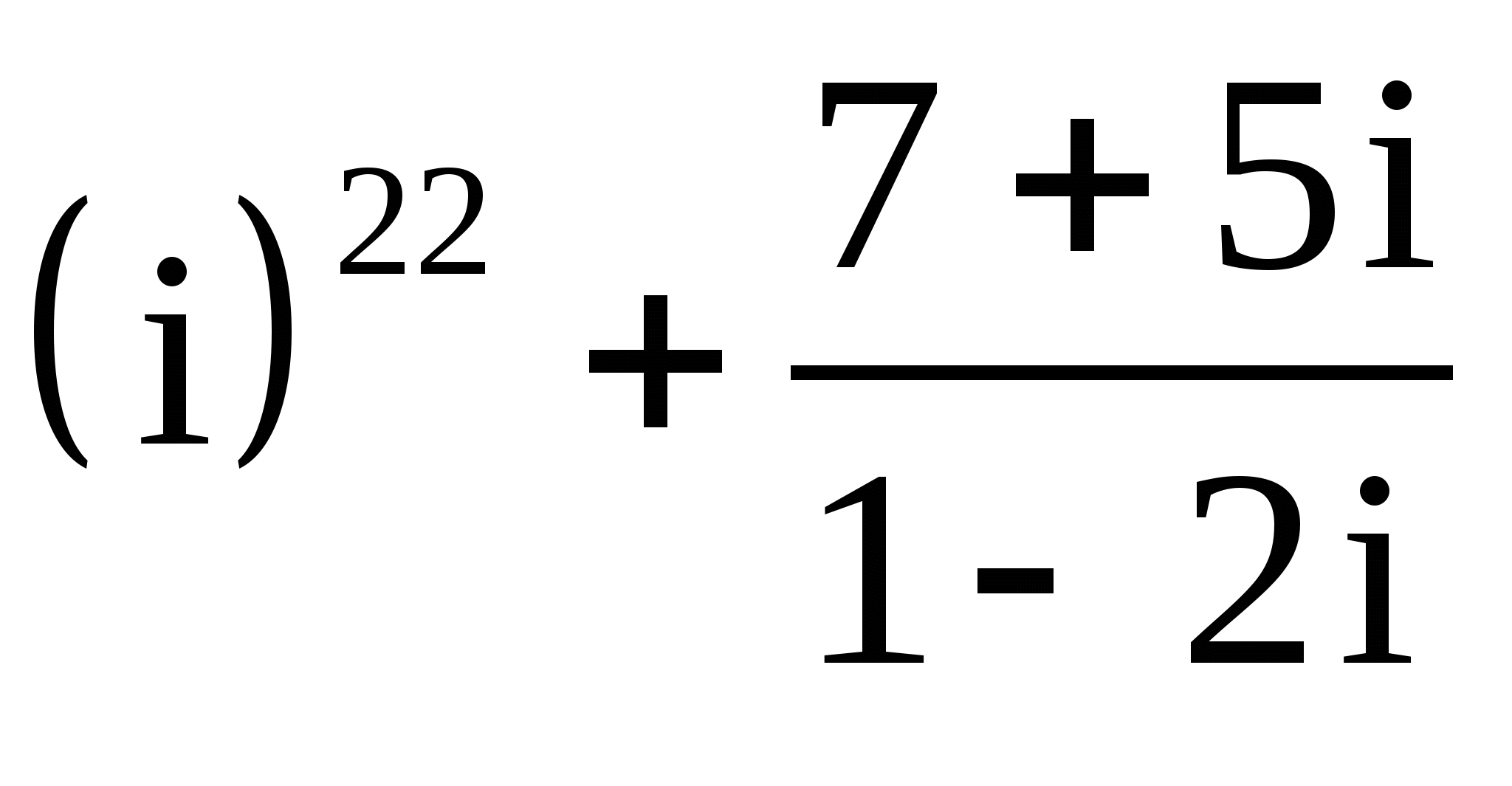 ;
;
7.
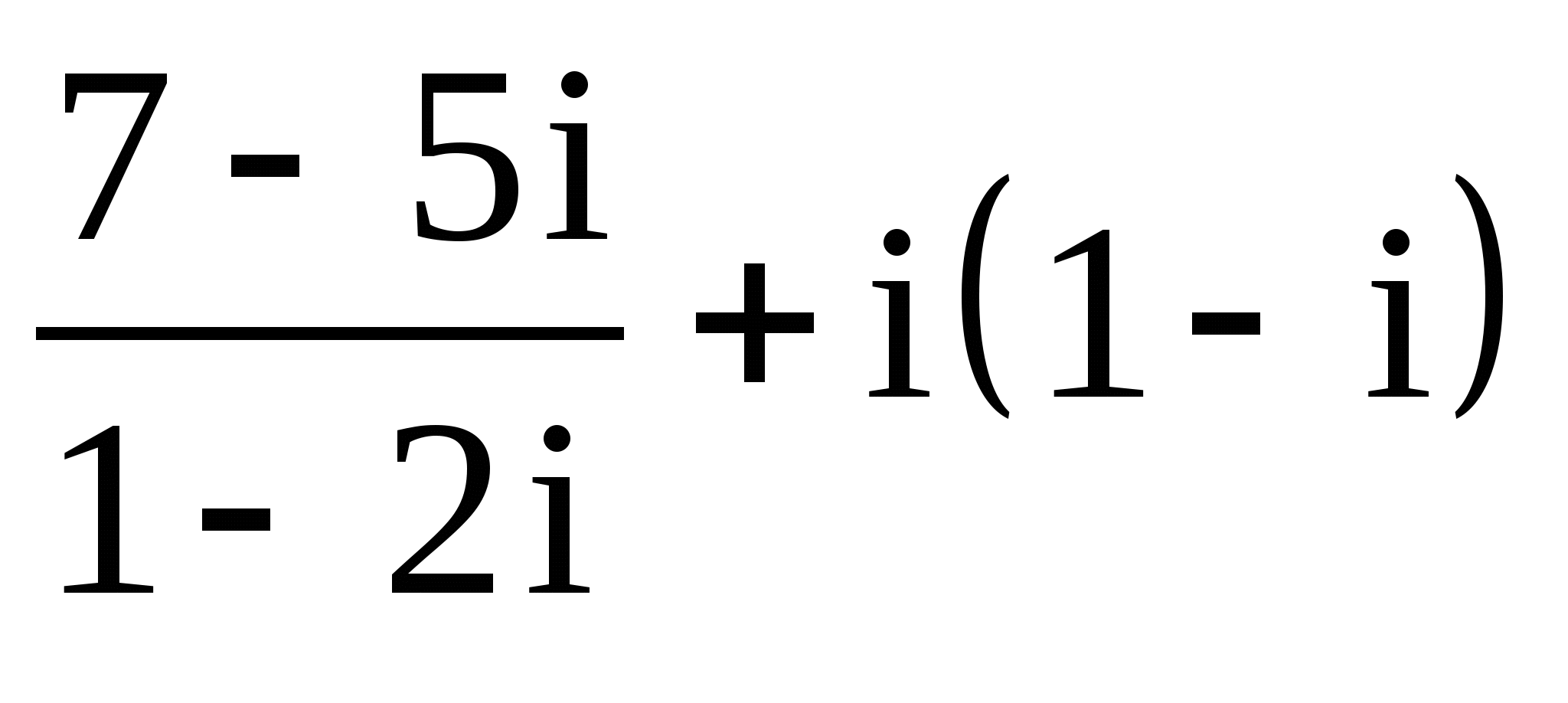 ;
;
8.
![]() ;
;
9.
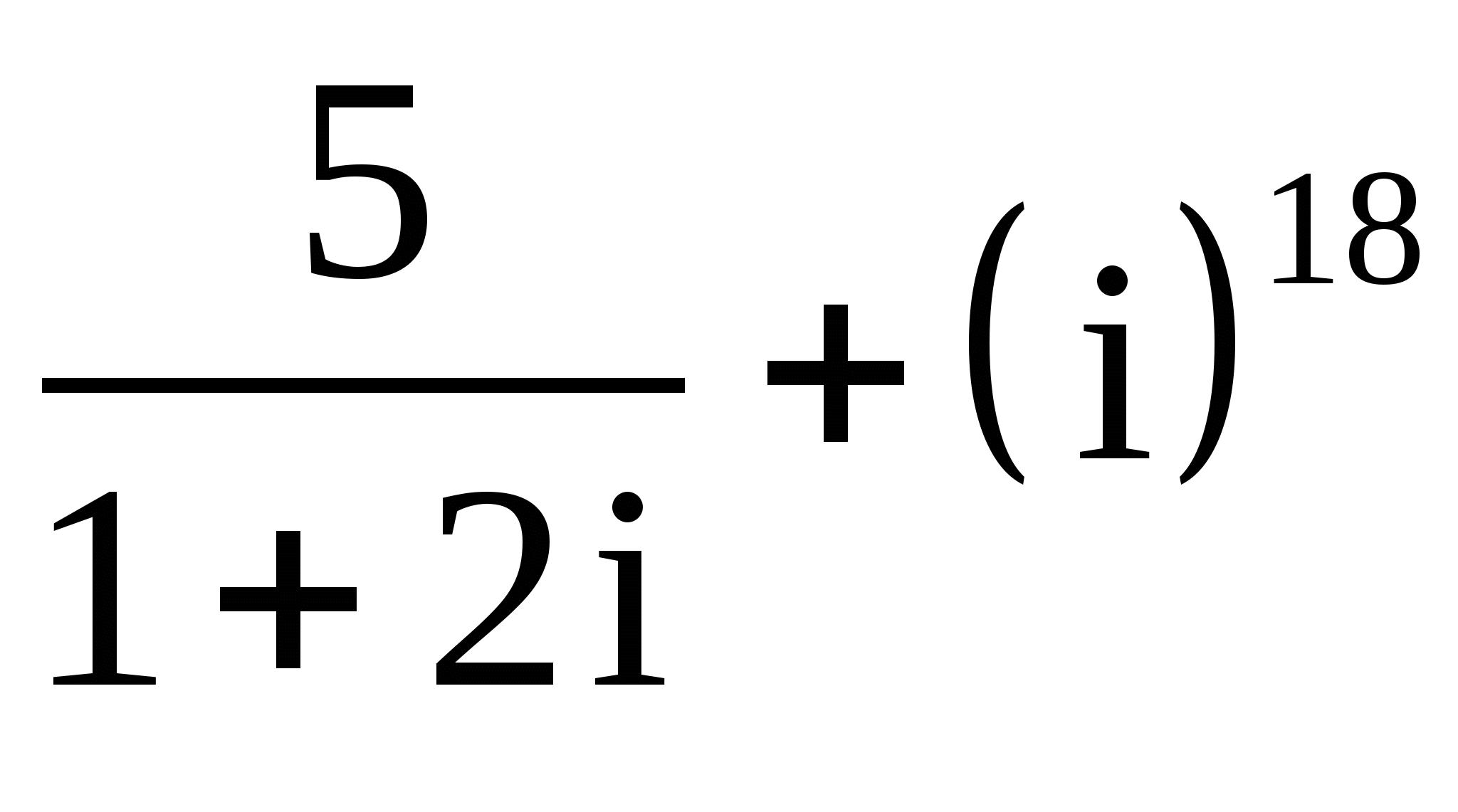 ;
;
10.
![]() ;
;
11.
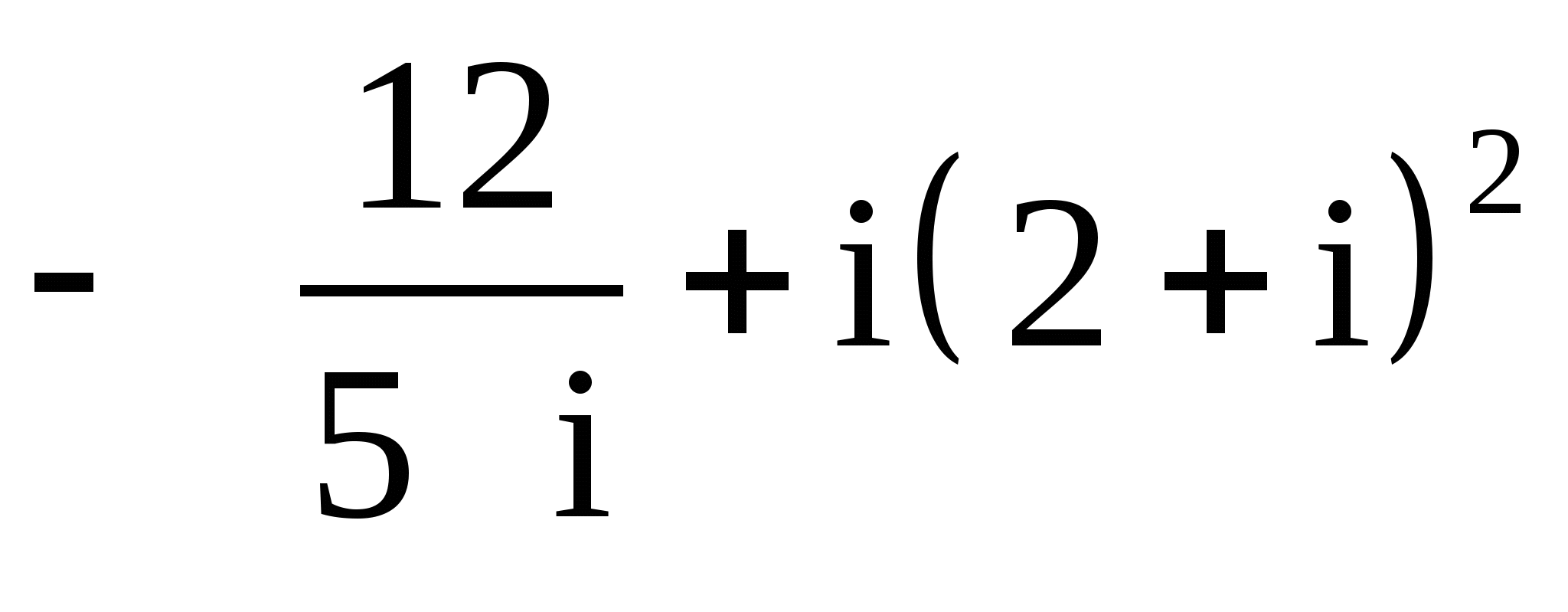 ;
;
12.
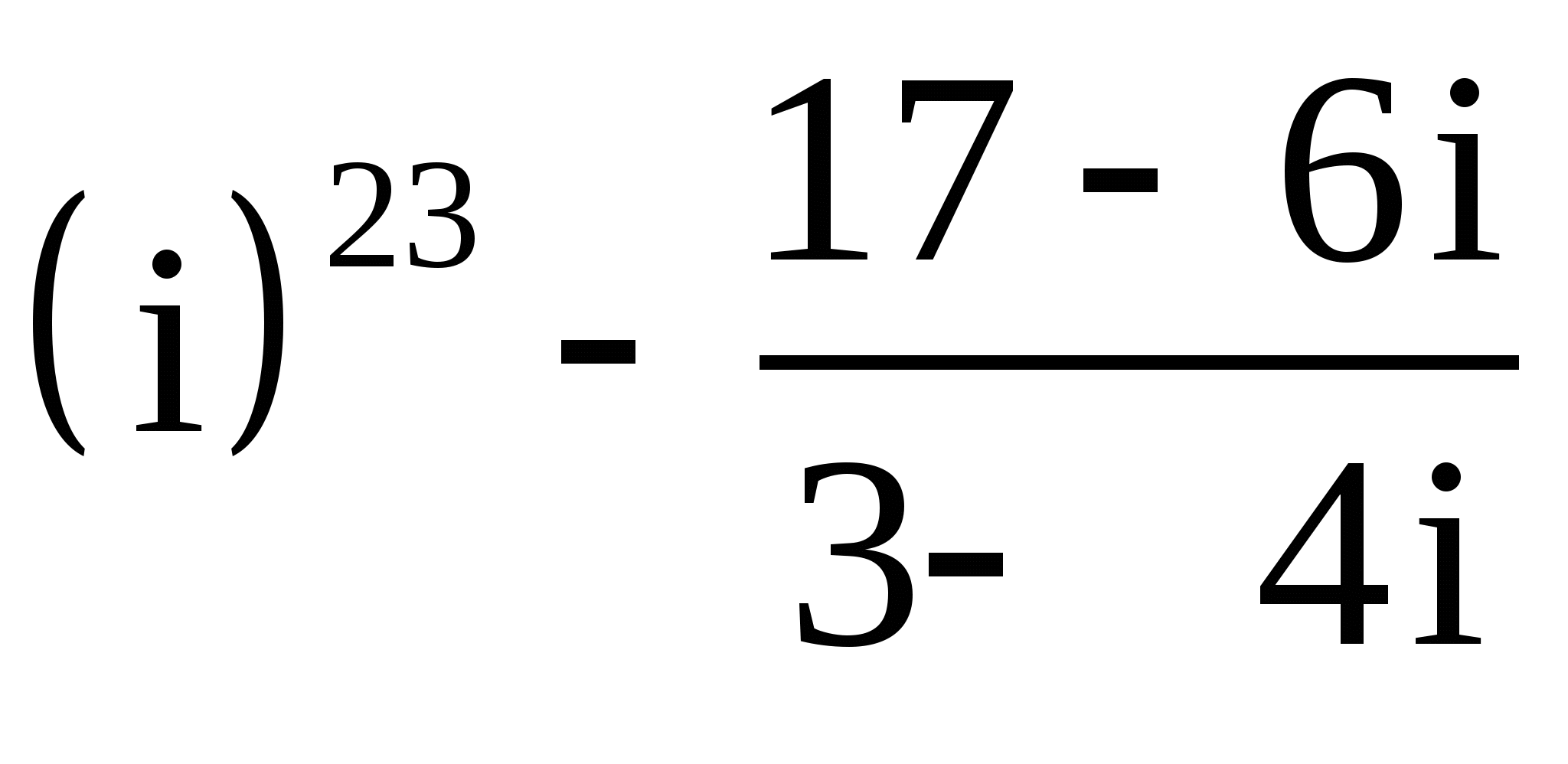 ;
;
13.
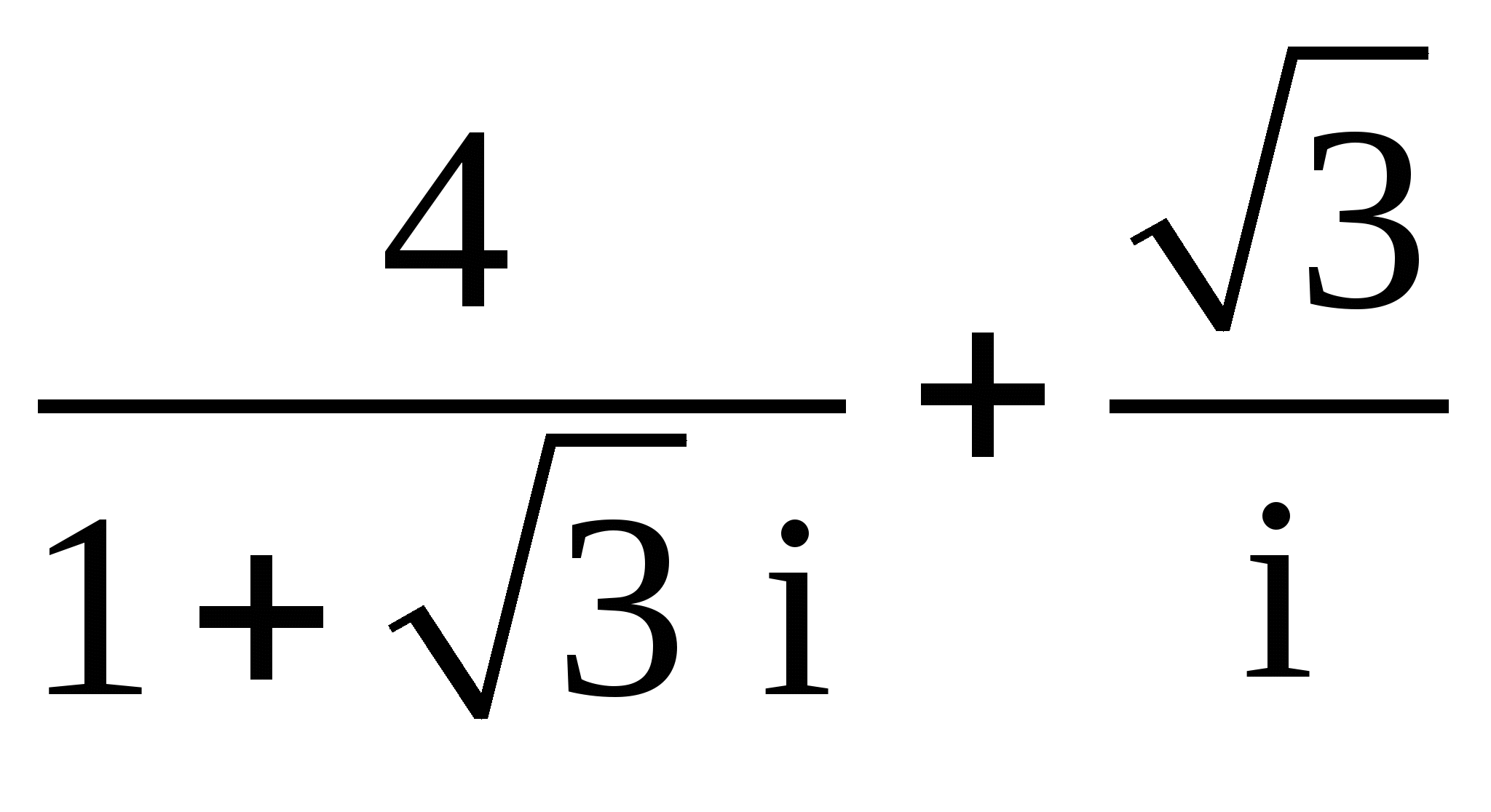 ;
;
14.
![]() ;
;
15.
![]() ;
;
16.
![]() ;
;
17.
![]() ;
;
18.
![]() ;
;
19.
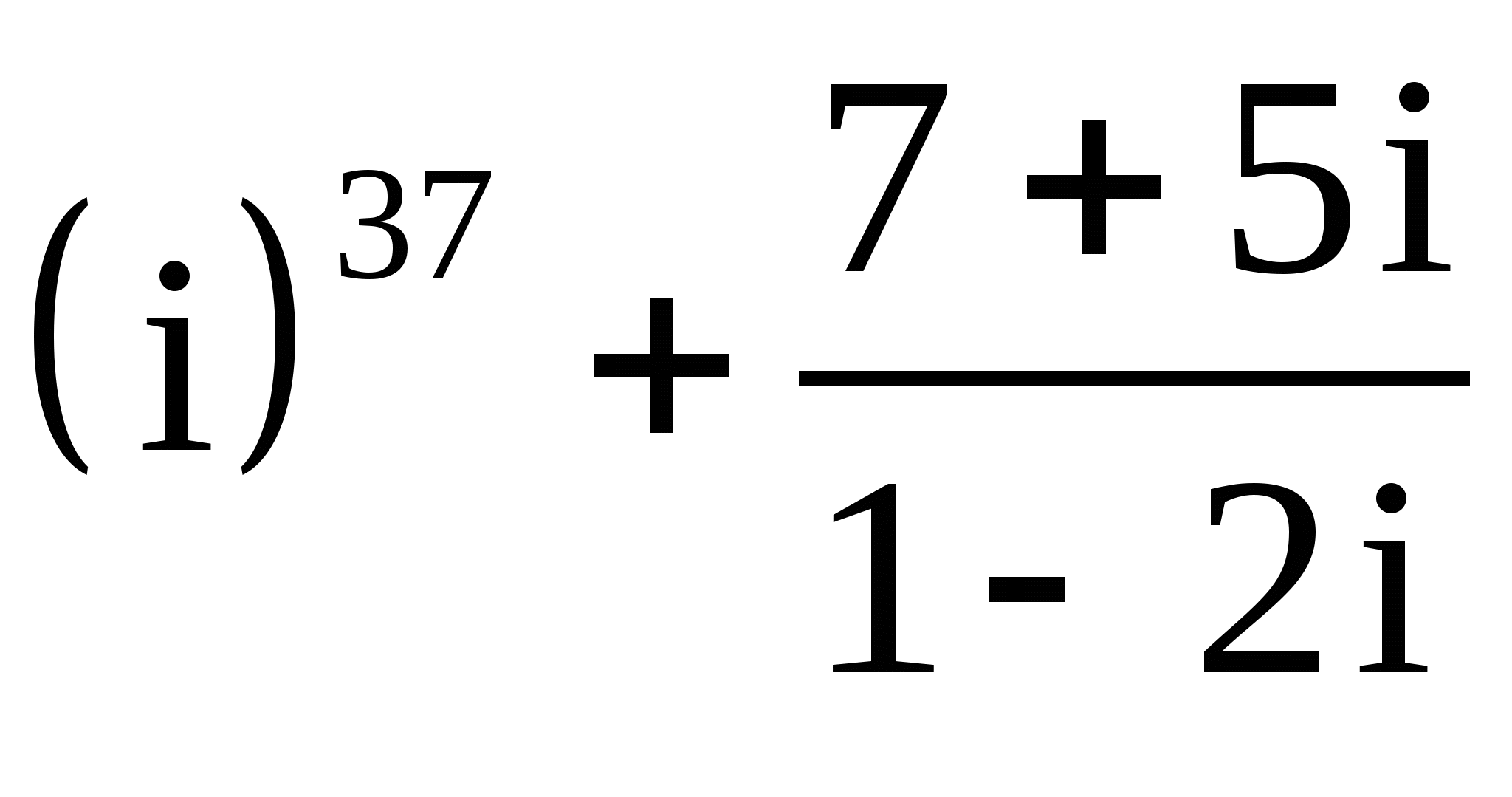 ;
;
20.
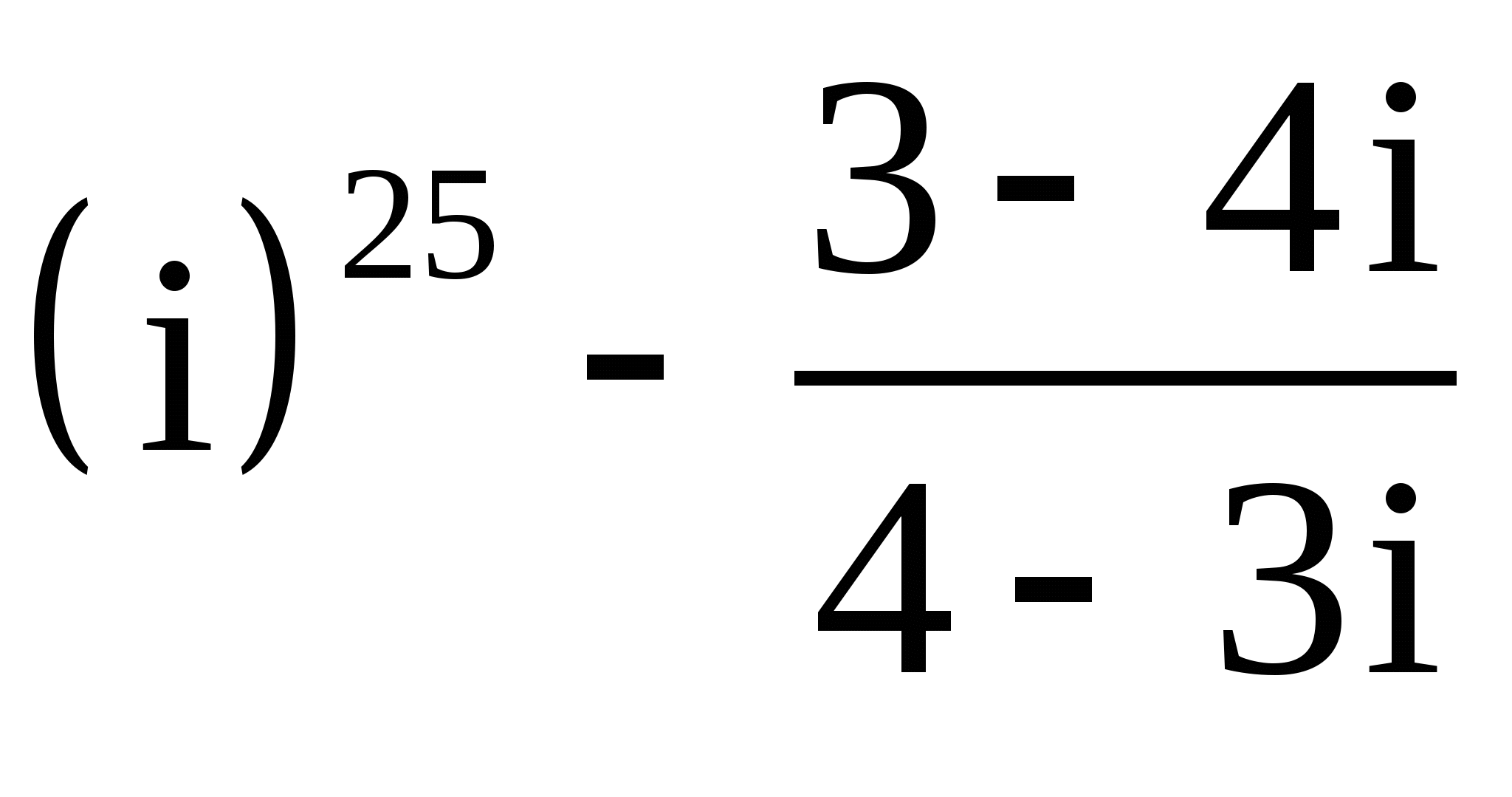 ;
;
21.
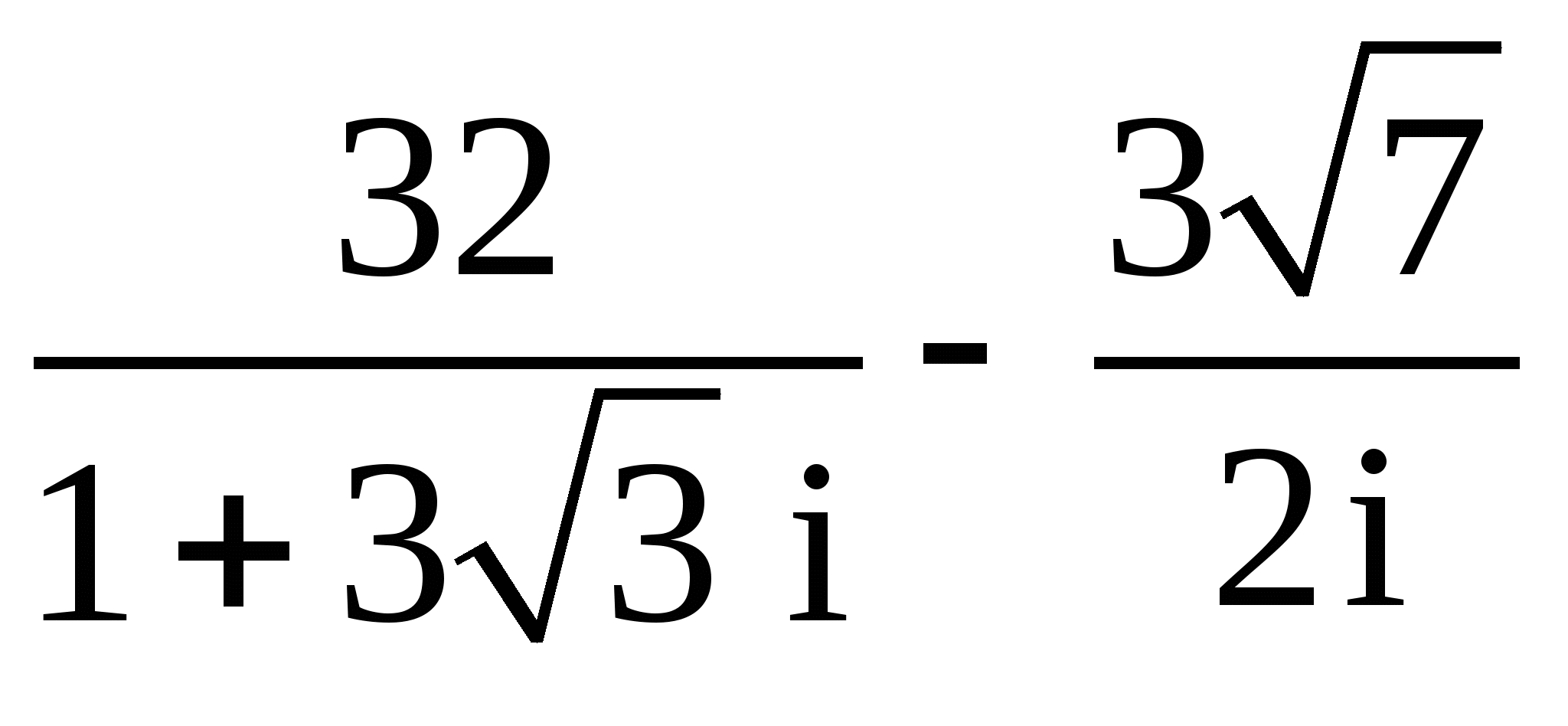 ;
;
22.
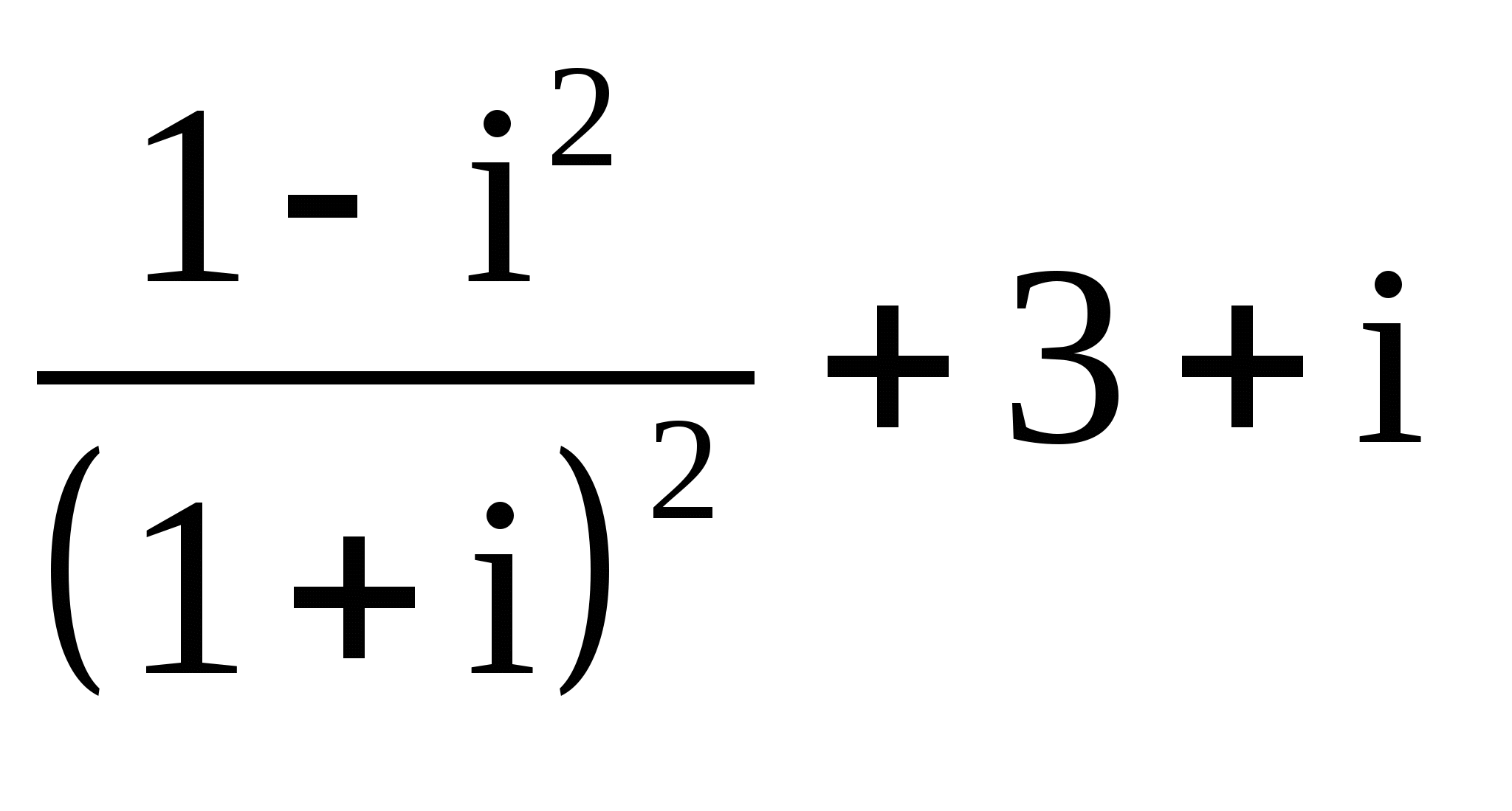 ;
;
23.
![]() ;
;
24.
![]() ;
;
25.
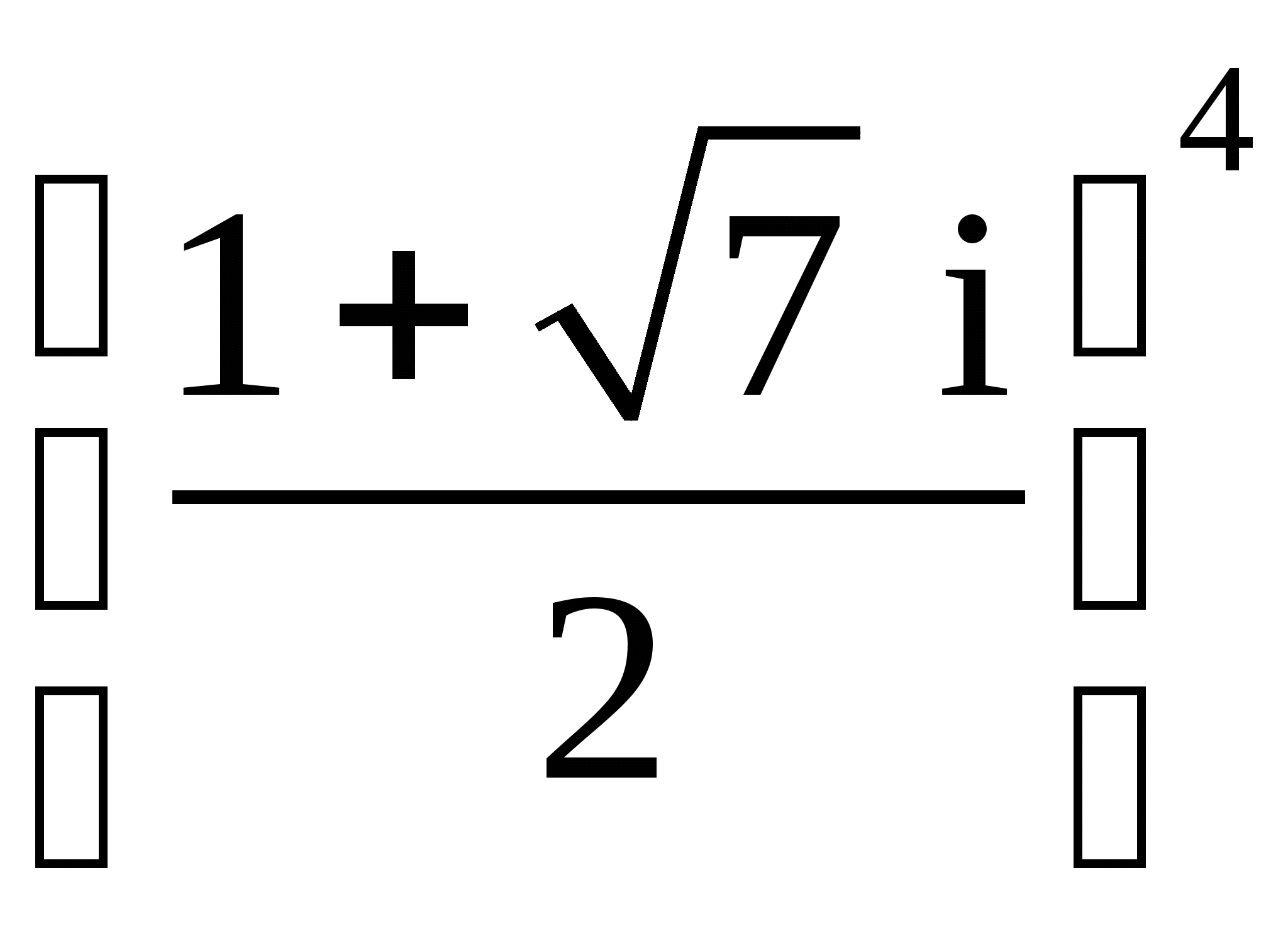 ;
;
26.
![]() ;
;
27.
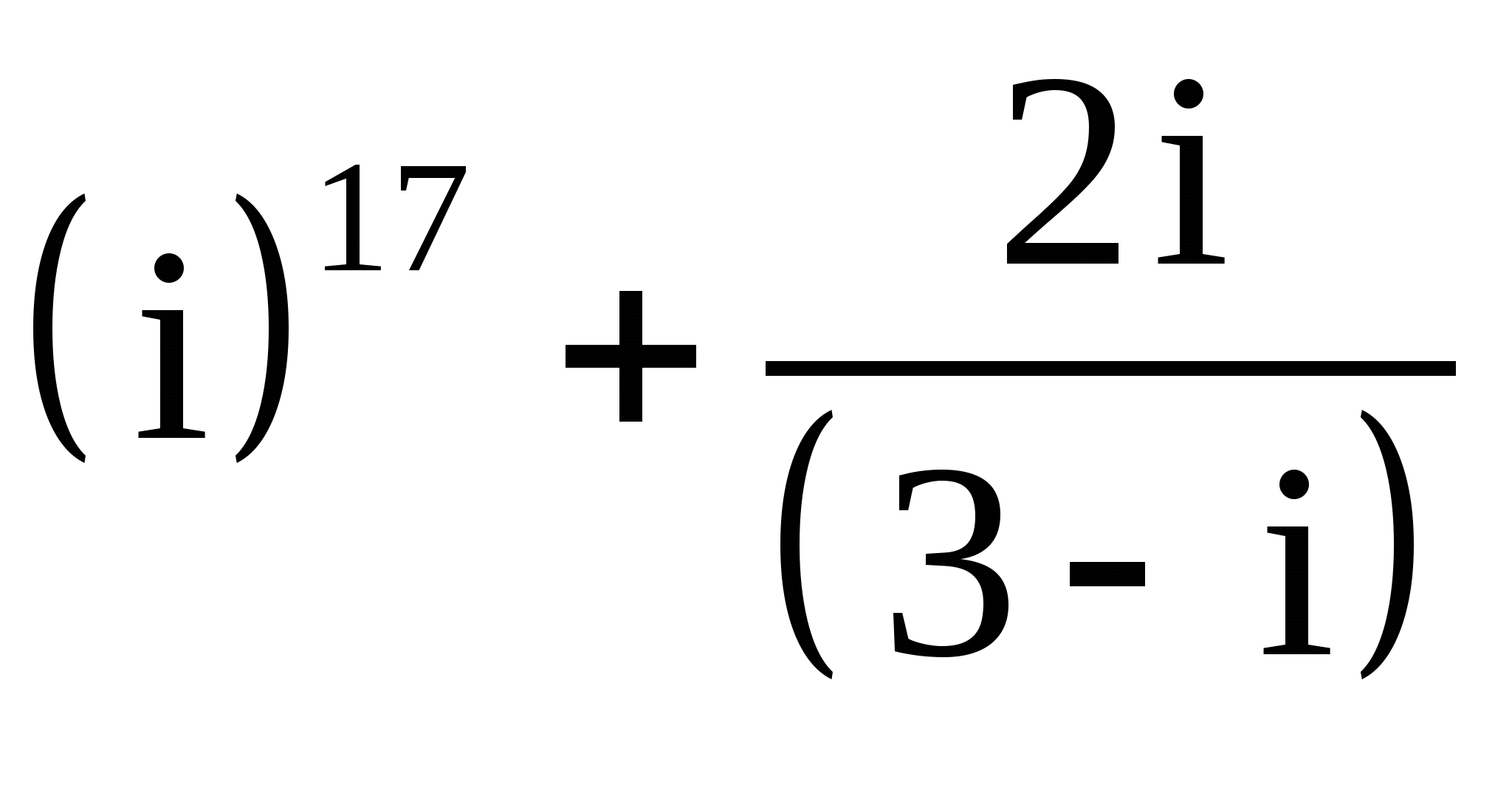 ;
;
28.
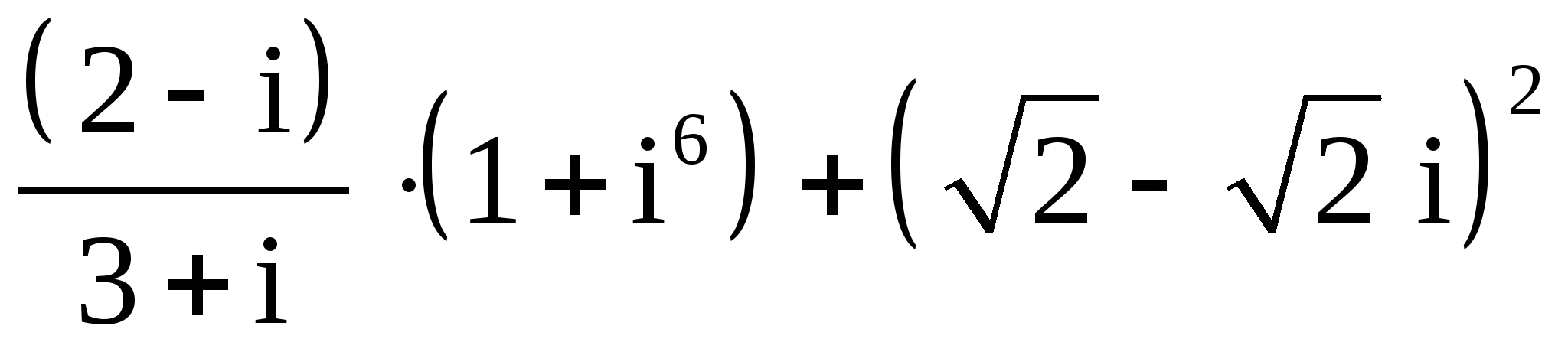 ;
;
29.
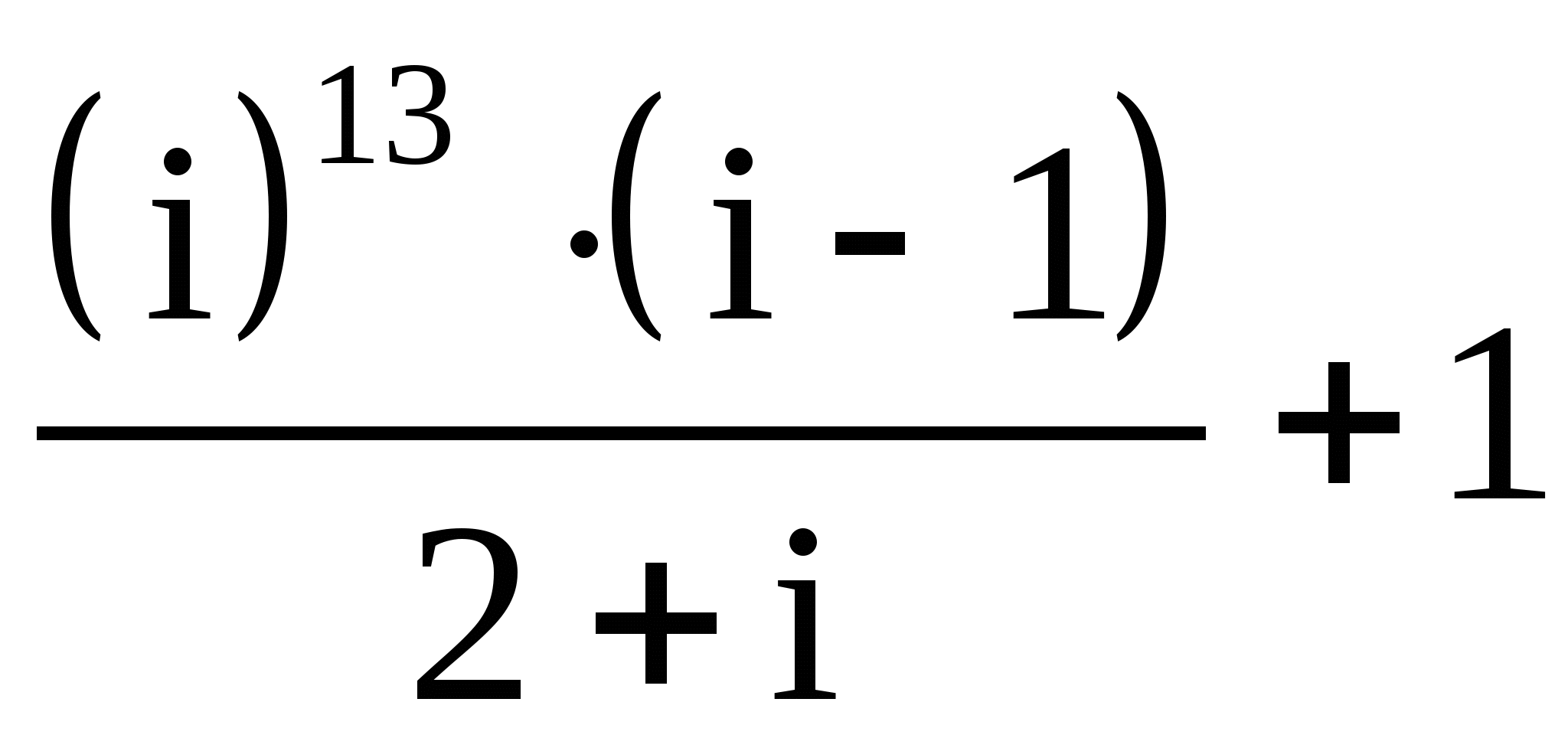 ;
;
30.
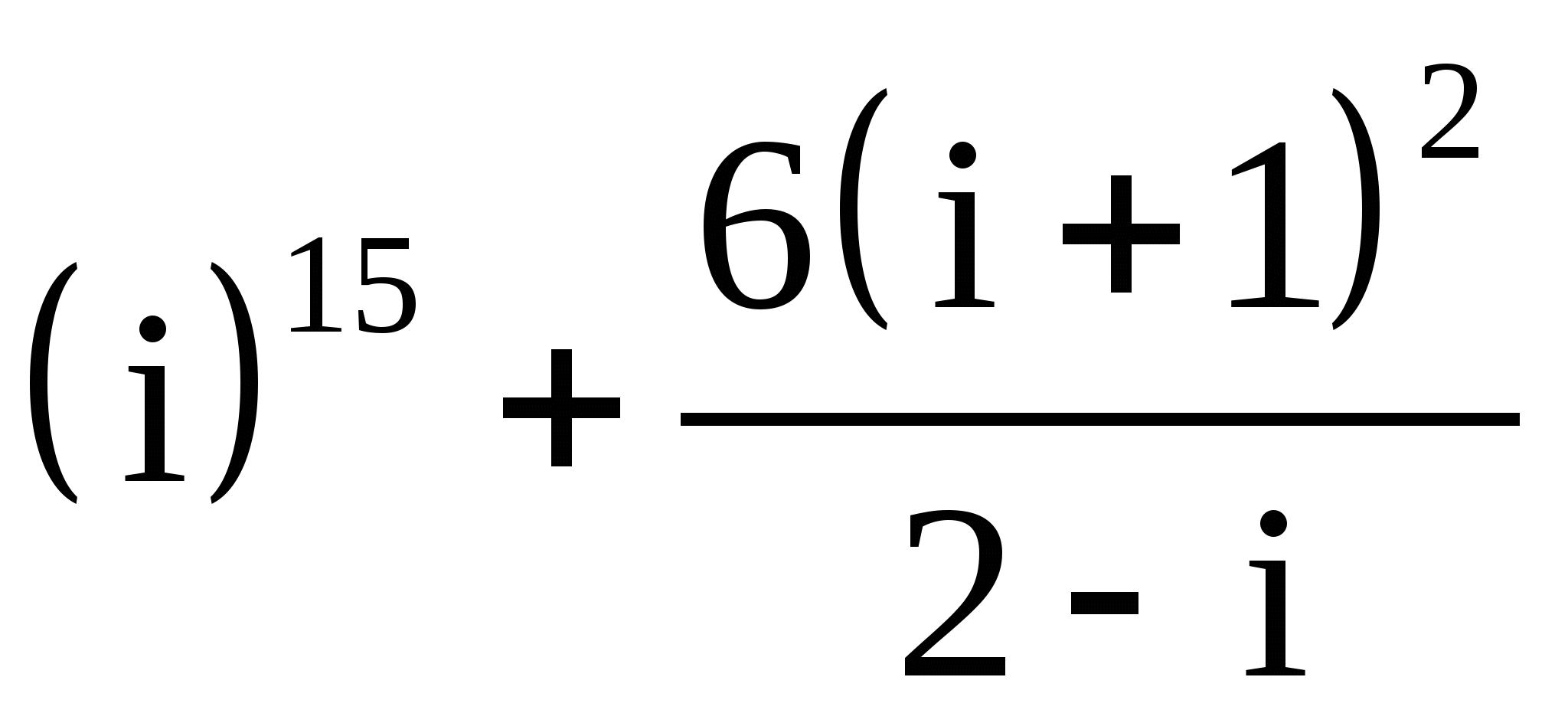 .
.
Задача 2
Представить комплексное число в тригонометрической форме:1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() ;
;
5.
![]() ;
;
6.
![]() ;
;
7.
![]() ;
;
8.
![]() ;
;
9.
![]() ;
;
10.
![]() ;
;
11.
![]() ;
;
12.
![]() ;
;
13.
![]() ;
;
14.
![]() ;
;
15.
![]() ;
;
16.
![]() ;
;
17.
![]() ;
;
18.
![]() ;
;
19.
![]() ;
;
20.
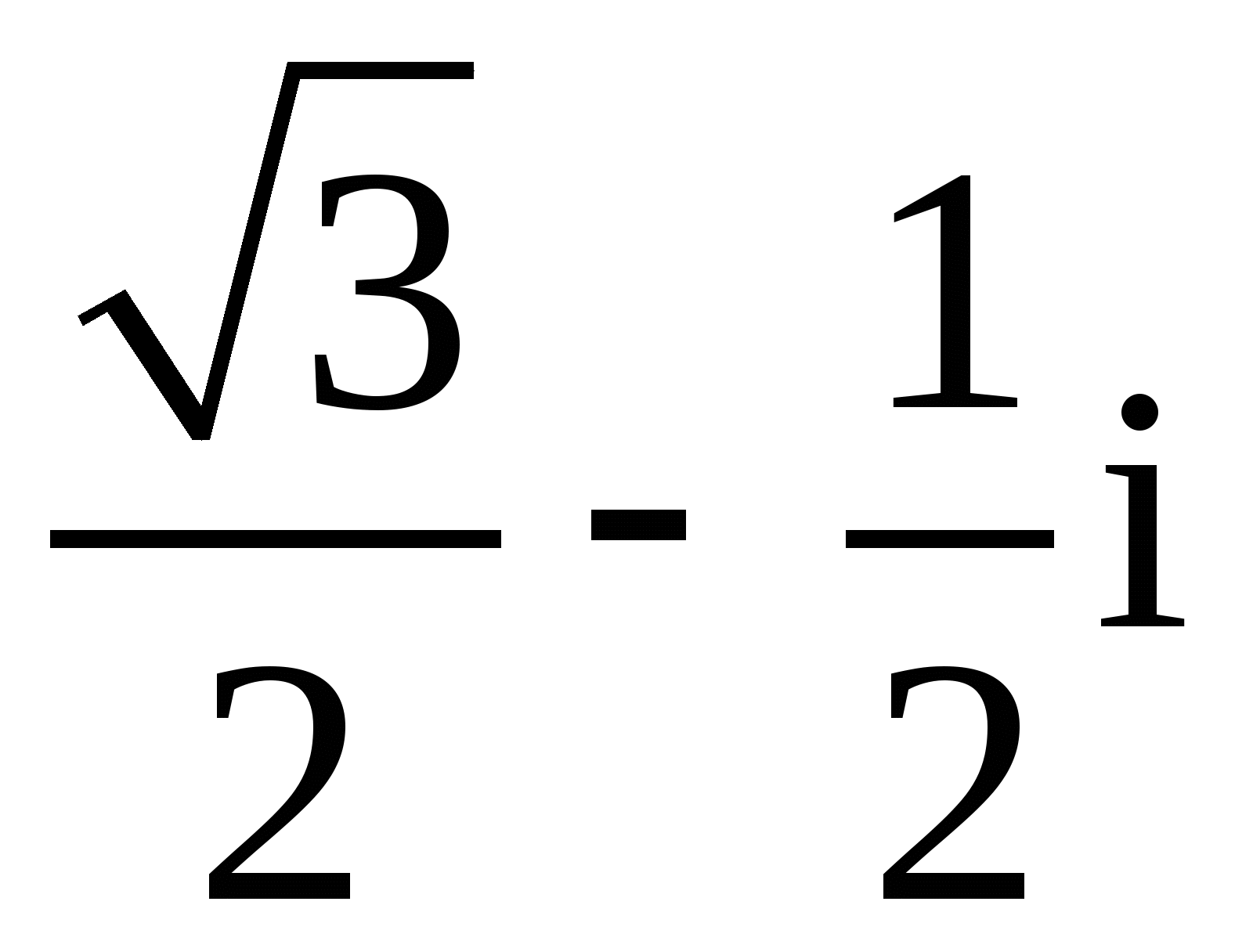 ;
;
21.
![]() ;
;
22.
![]() ;
;
23.
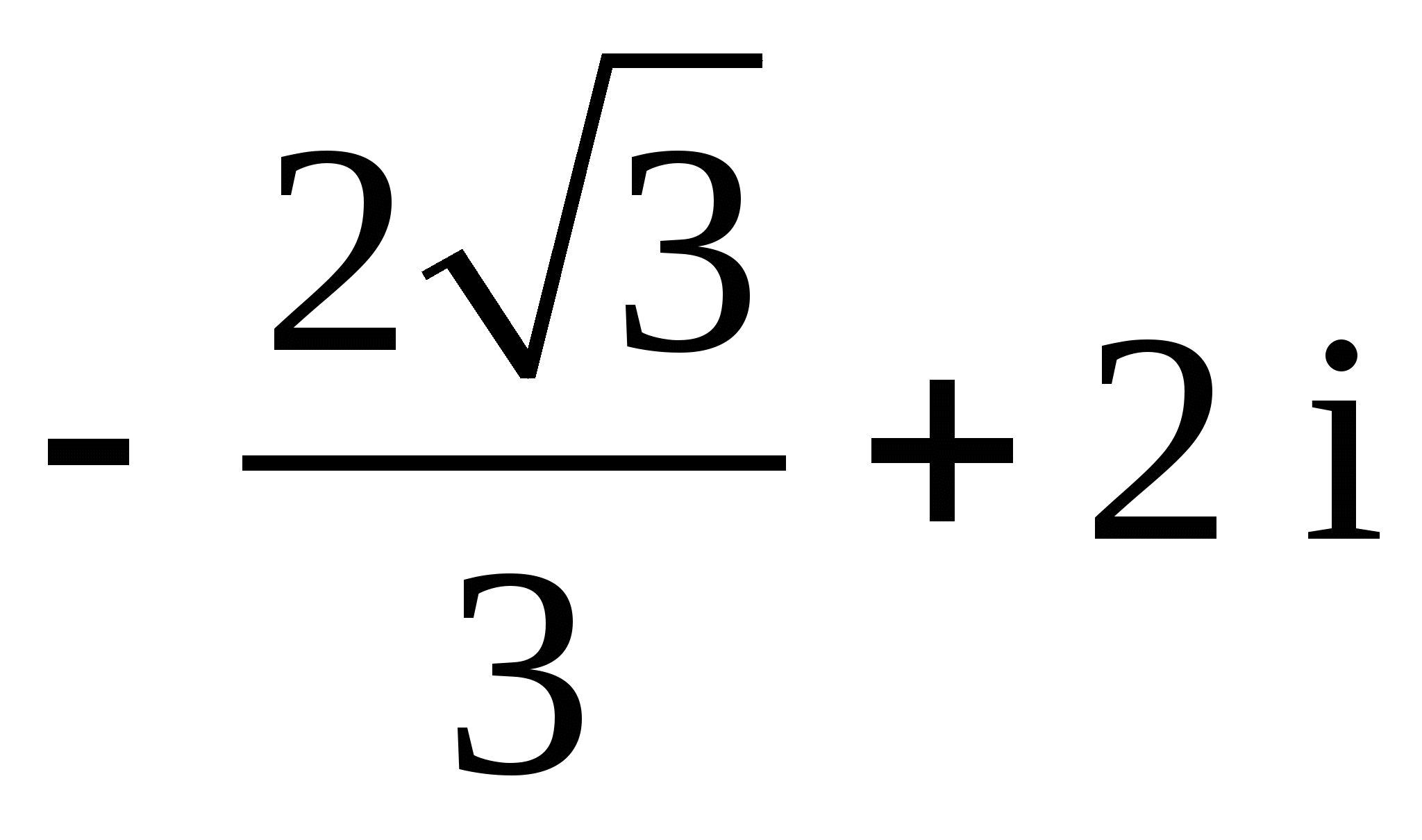 ;
;
24.
![]() ;
;
25.
![]() ;
;
26.
![]() ;
;
27.
![]() ;
;
28.
![]() ;
;
29.
![]() ;
;
30.
![]() .
.
Задача 3
Вычислить корень:;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() ;
;
5.
![]() ;
;
6.
![]() ;
;
7.
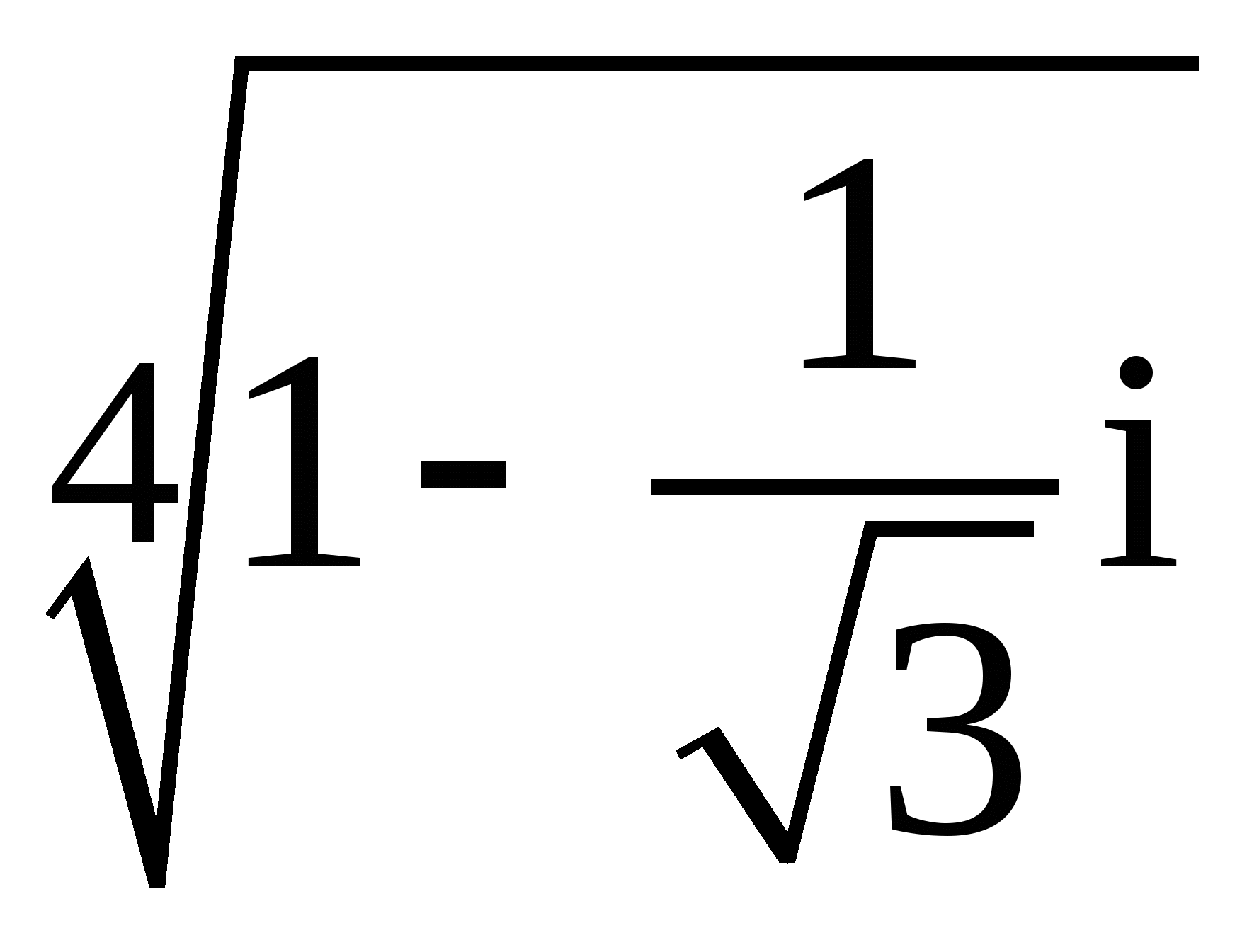 ;
;
8.
![]() ;
;
9.
![]() ;
;
10.
![]() ;
;
11.
![]() ;
;
Решить уравнение:
12.
![]() ;
;
13.
![]() ;
;
14.
![]() ;
;
15.
![]() ;
;
16.
![]() ;
;
17.
![]() ;
;
18.
![]() ;
;
19.
![]() ;
;
20.
![]()
21.
![]() ;
;
22.
![]() ;
;
23.
![]() ;
;
24.
![]() ;
;
25.
![]() ;
;
26.
![]() ;
;
27.
![]() ;
;
28.
![]() ;
;
29.
![]() ;
;
30.
![]()
Задача 4
Представить число в показательной форме:1.
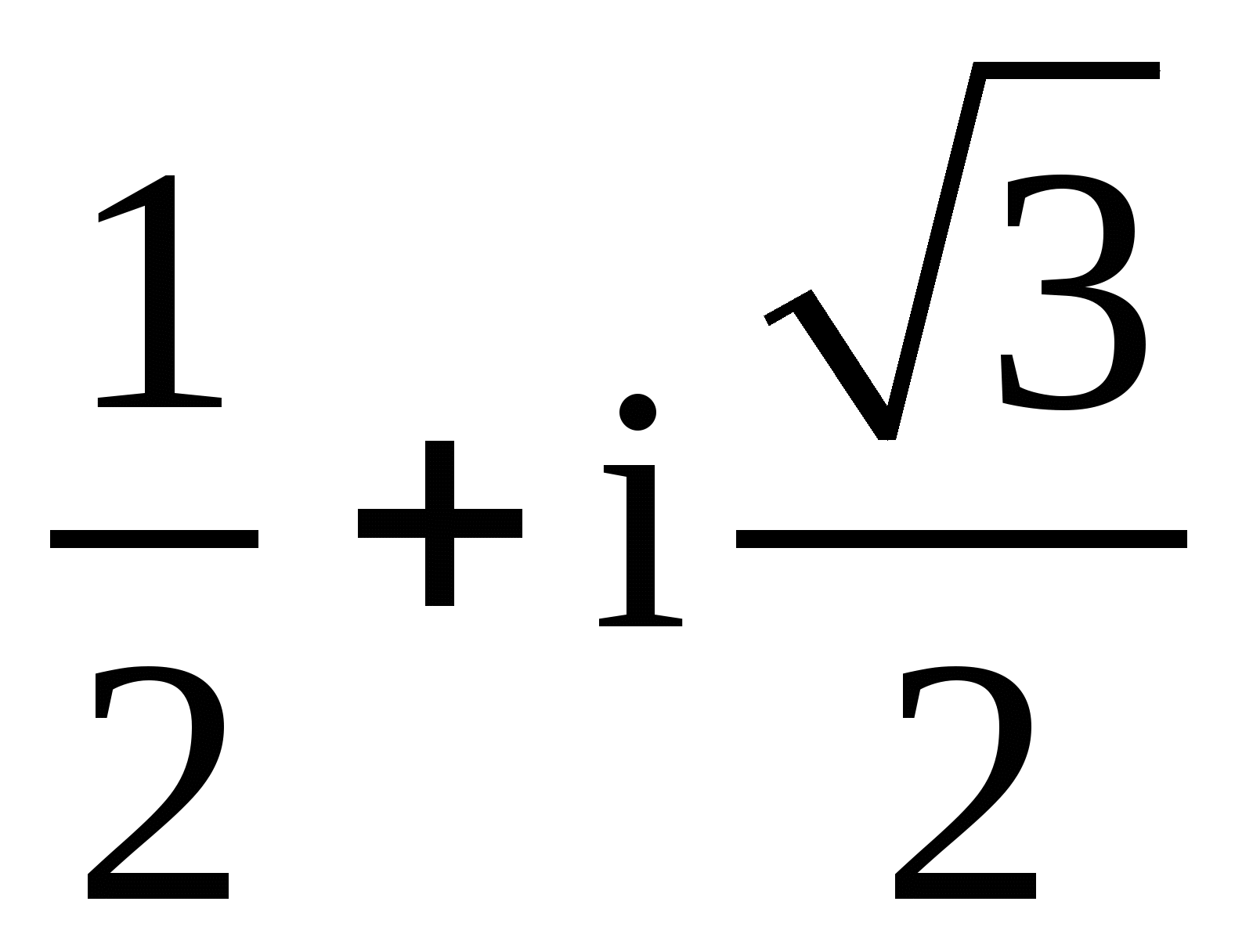 ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() ;
;
5.
![]() ;
;
6.
![]() ;
;
7.
![]() ;
;
8.
![]() ;
;
9.
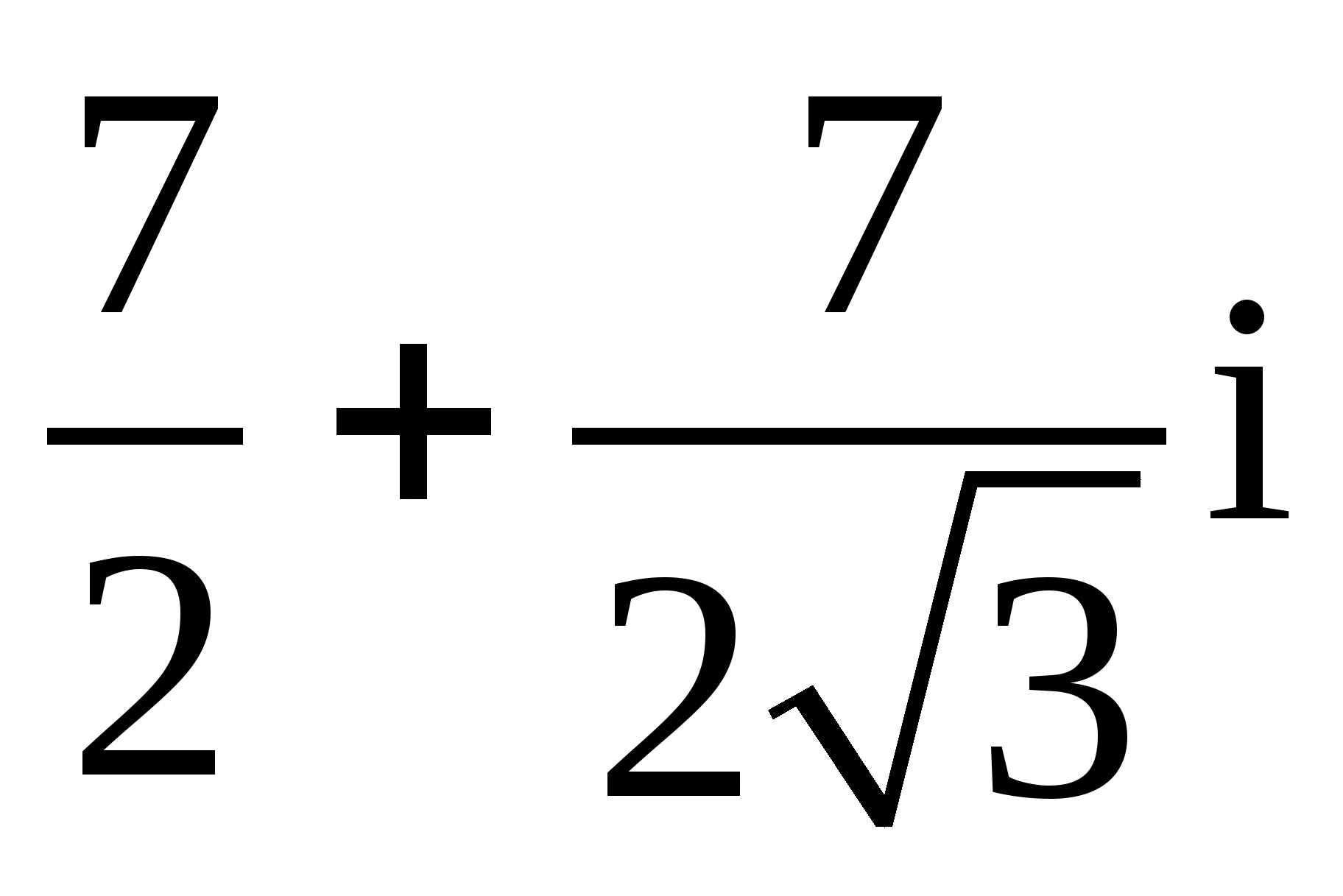 ;
;
10.
![]() ;
;
11.
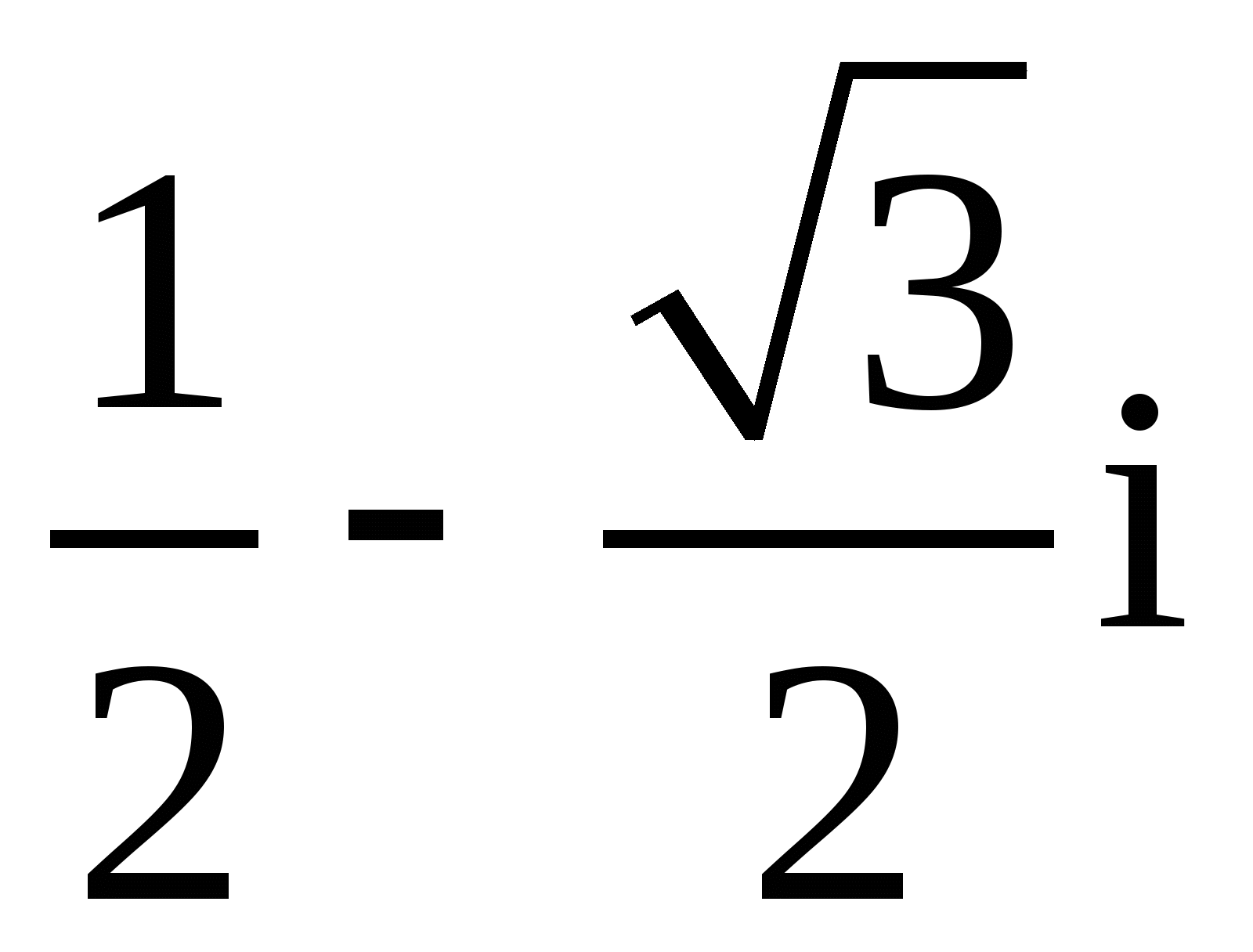 ;
;
12.
![]() ;
;
13.
![]() ;
;
14.
![]() ;
;
15.
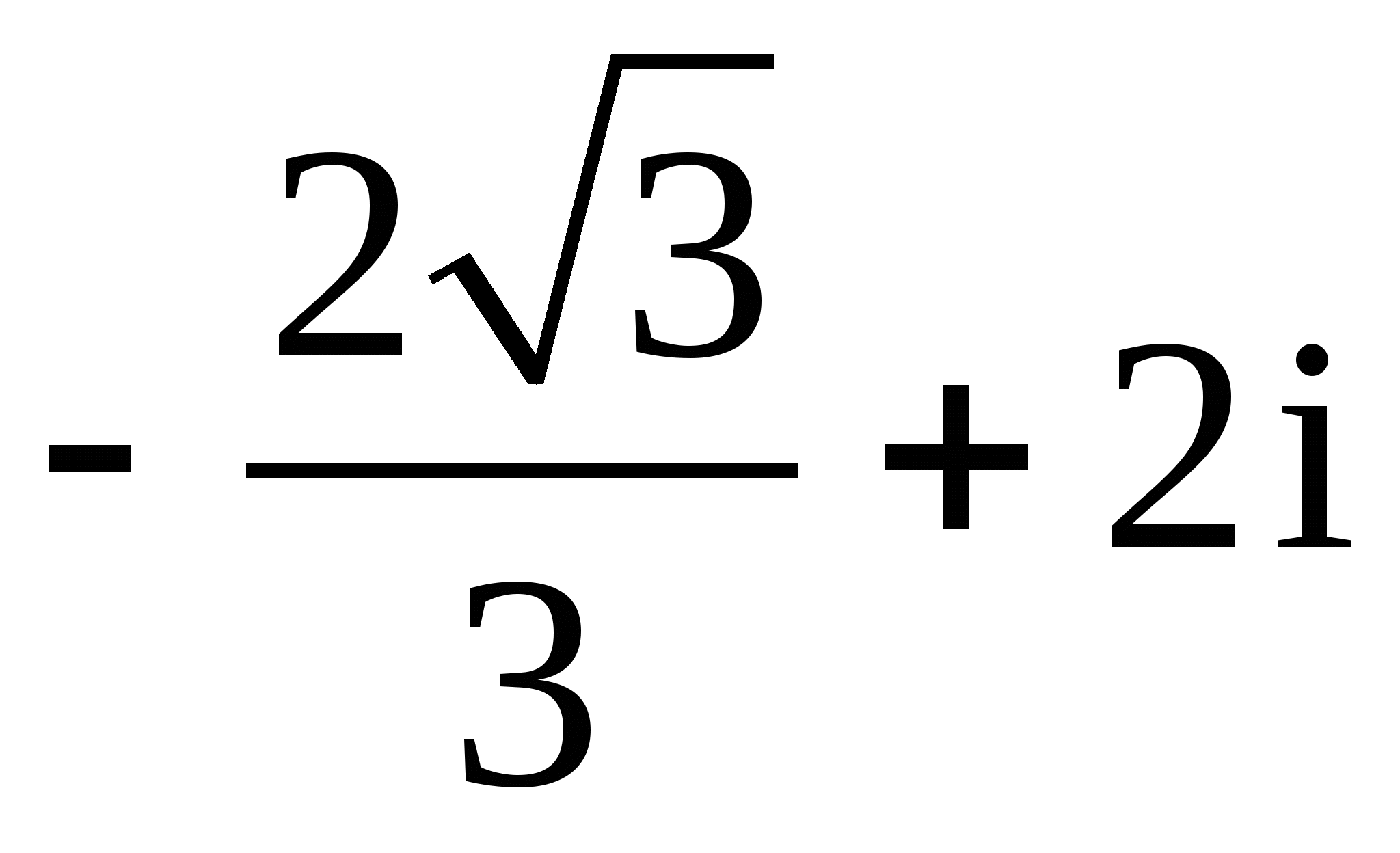 ;
;
16.
![]() ;
;
17.
![]() ;
;
18.
![]() ;
;
19.
![]() ;
;
20.
![]() ;
;
21.
![]() ;
;
22.
![]() ;
;
23.
![]() ;
;
24.
![]() ;
;
25.
![]() ;
;
26.
![]() ;
;
27.
![]() ;
;
28.
![]() ;
;
29.
![]() ;
;
30.
![]() .
.
Задача 5
Определить и построить множество точек, удовлетворяющих данным уравнениям или неравенствам:1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() ;
;
5.
![]() ;
;
6.
![]() ;
;
7.
![]() ;
;
8.
![]() ;
;
9.
![]() ;
;
10.
![]() ;
;
11.
![]() ;
;
12.
![]() ;
;
13.
![]() ;
;
14.
![]() ;
;
15.
![]() ;
;
16.
![]() ;
;
17.
![]() ;
;
18.
![]() ;
;
19.
![]() ;
;
20.
![]() ;
;
21.
![]() ;
;
22.
![]() ;
;
23.
![]() ;
;
24.
![]() ;
;
25.
![]() ;
;
26.
![]() ;
;
27.
![]() ;
;
28.
![]() ;
;
29.
![]() ;
;
30.
![]() .
.
Задача 6
Найти действительную и мнимую части:1.
![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5. ![]() ;
;
6. ![]() ;
;
7. 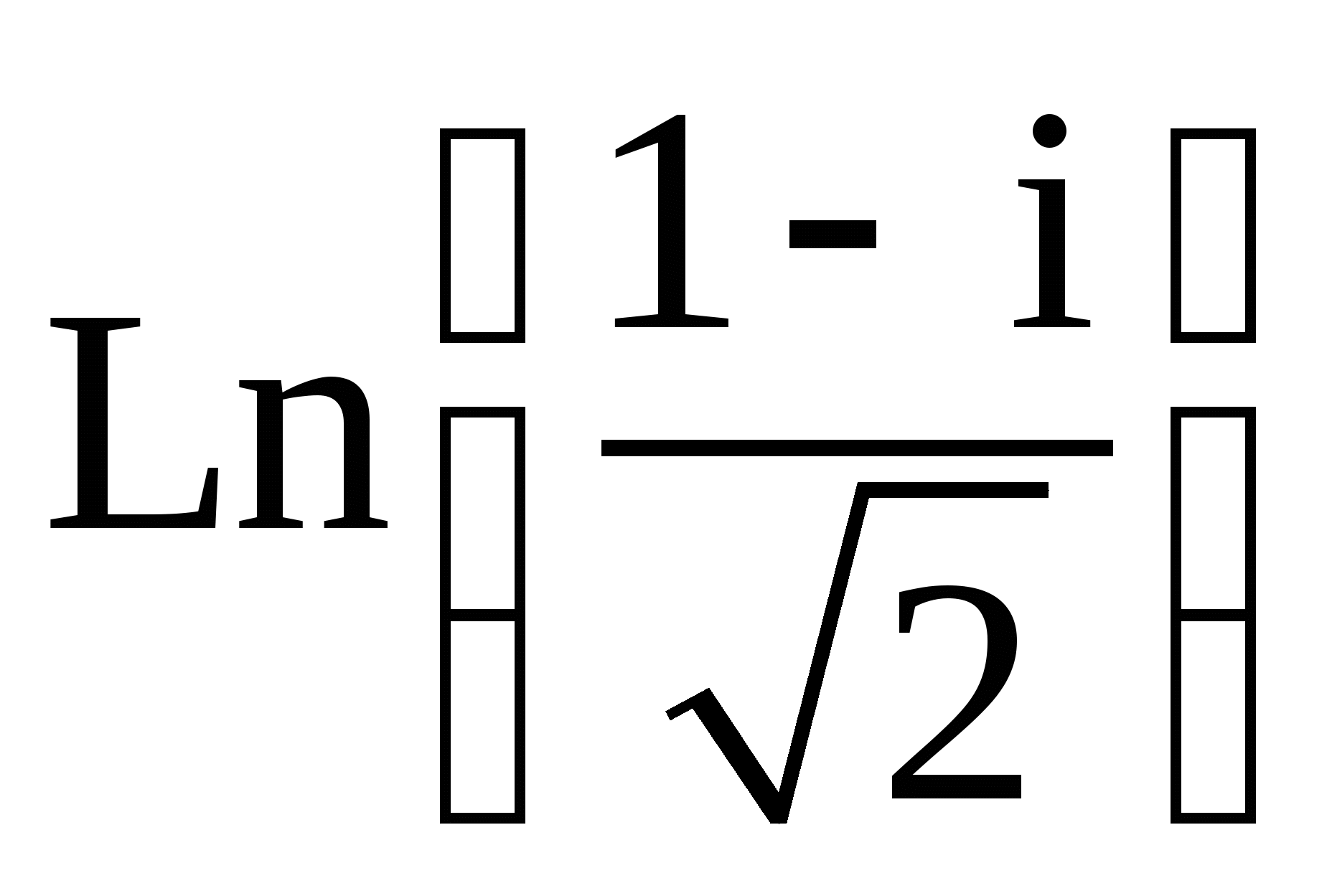 ;
;
8. ![]() ;
;
9. ![]() ;
;
10. ![]() ;
;
11. ![]() ;
;
12. 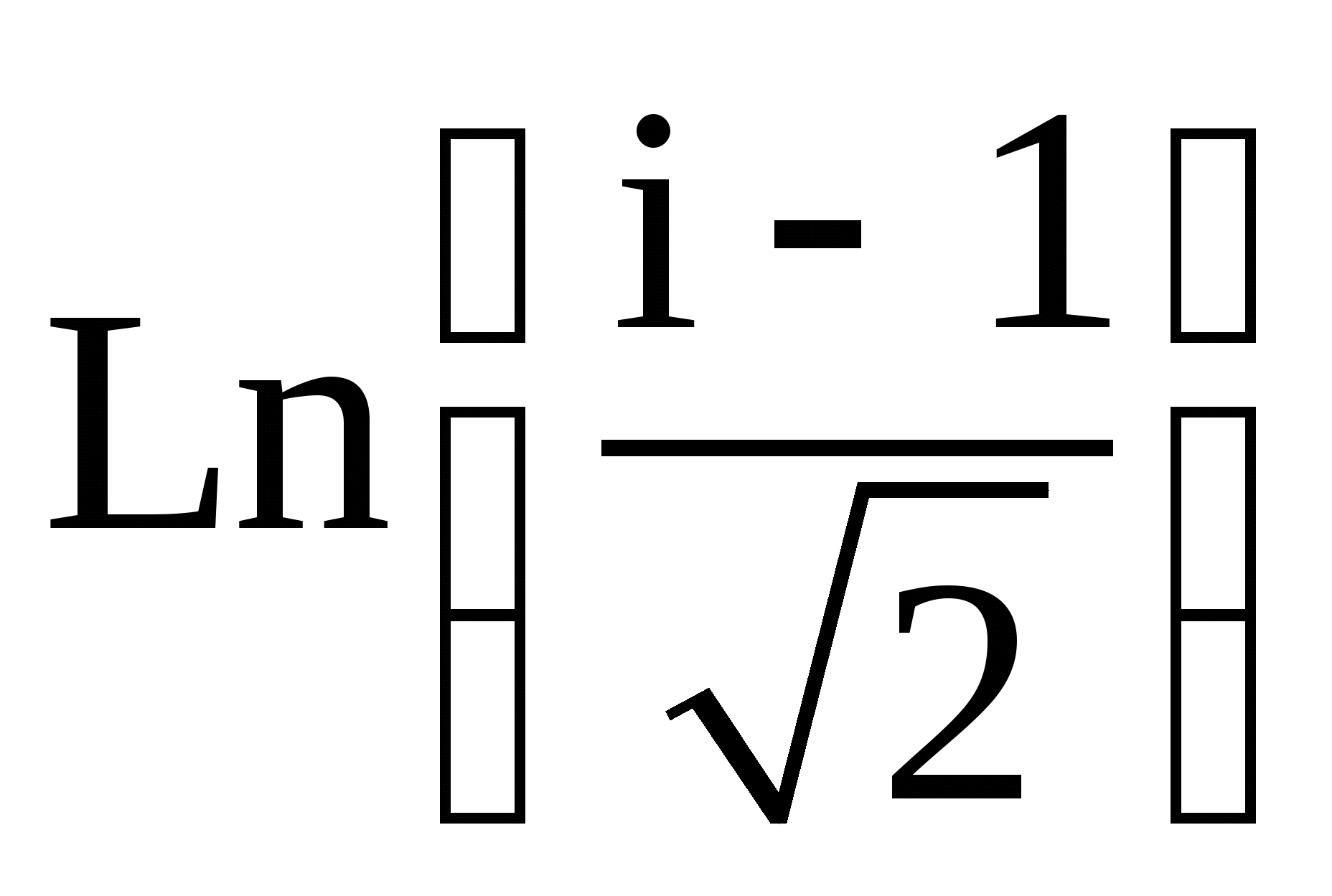 ;
;
13. ![]() ;
;
14. ![]() ;
;
15. ![]() ;
;
16. ![]() ;
;
17. ![]() ;
;
18. ![]() ;
;
19. ![]() ;
;
20. ![]() ;
;
21. 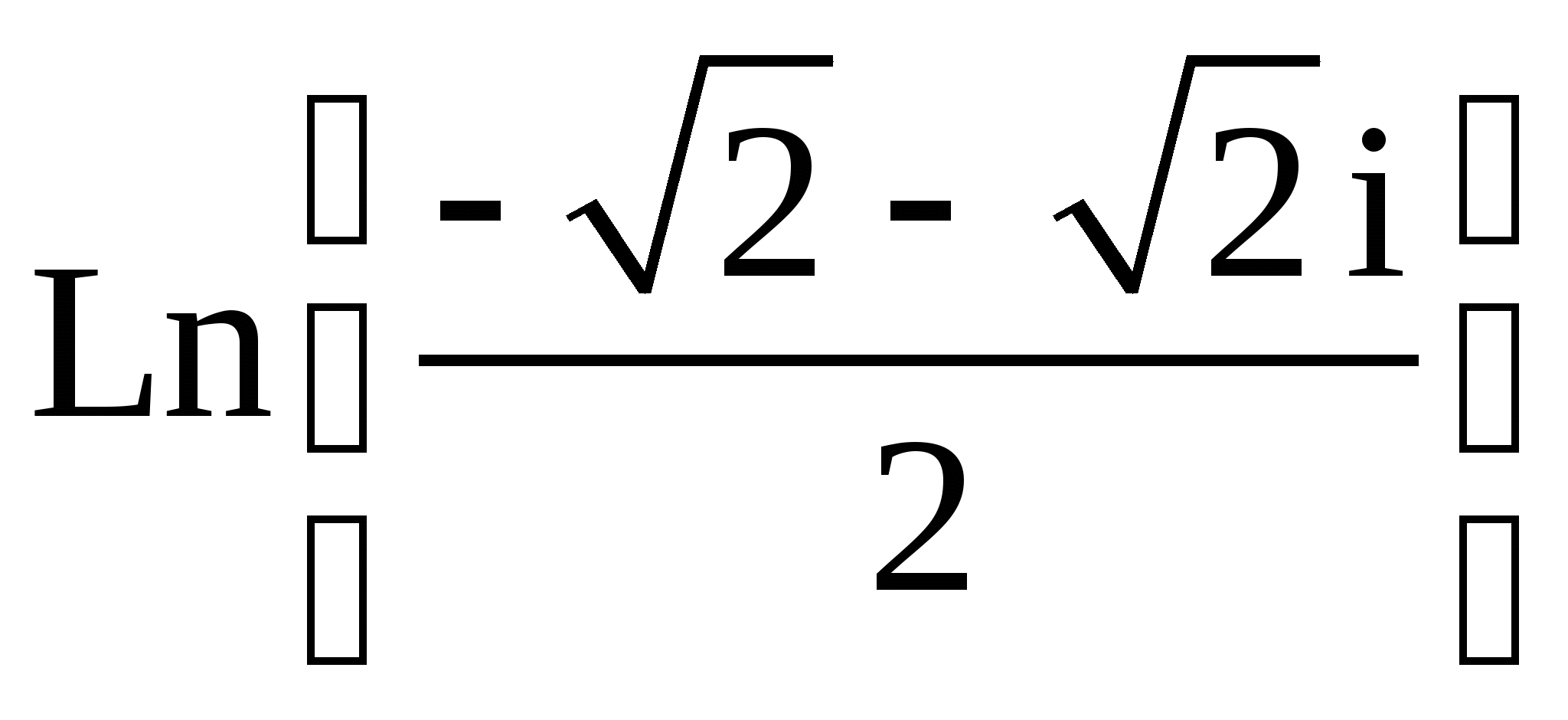 ;
;
22. ![]() ;
;
23. ![]() ;
;
24. ![]() ;
;
25. ![]() ;
;
26. ![]() ;
;
27. ![]() ;
;
28. ![]() ;
;
29. ![]() ;
;
30. ![]() .
.
Задача 7
Найти аналитическую функцию ![]() по следующим данным,
если
по следующим данным,
если ![]() :3.
:3. ![]() ;
;
4. ![]() ;
;
5. ![]() ;
;
6. ![]() ;
;
7. 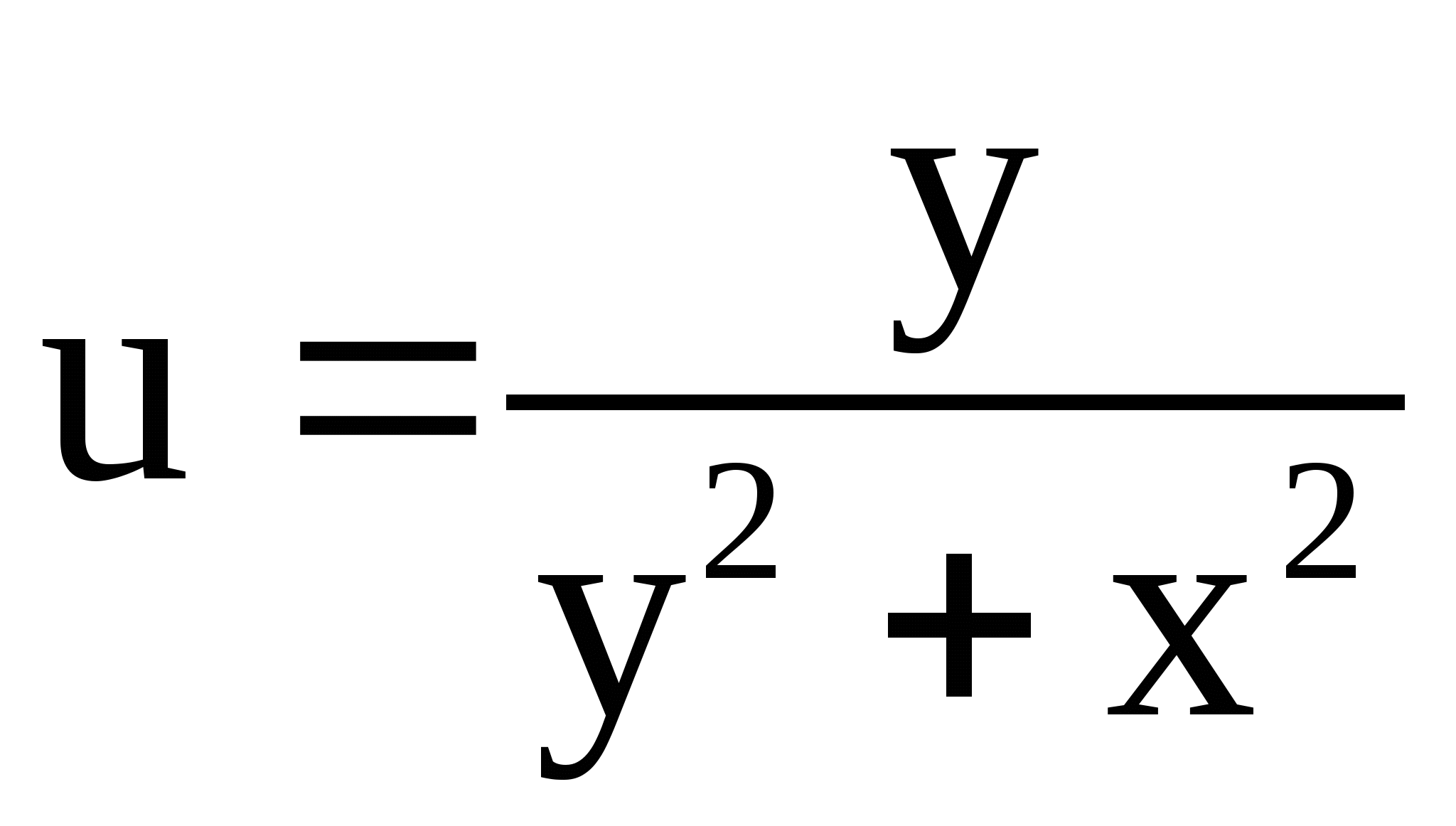 ;
;
8. ![]() ;
;
9. ![]() ;
;
10. ![]() ;
;
11. ![]() ;
;
12. ![]() ;
;
13. 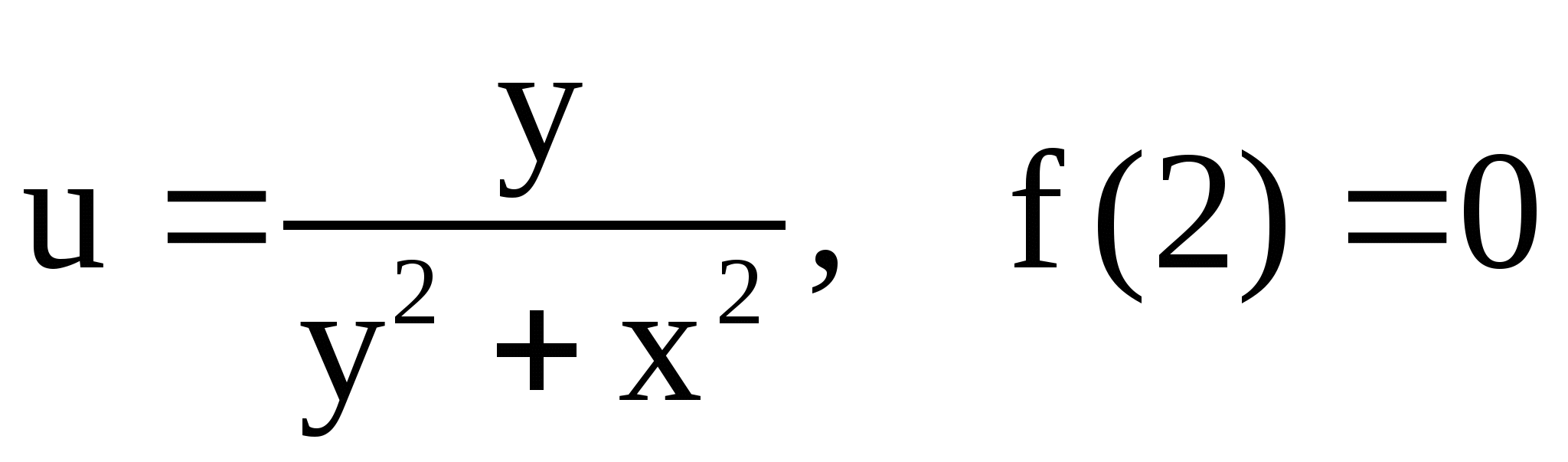 ;
;
14. ![]() ;
;
15. ![]() ;
;
16. ![]() ;
;
17. 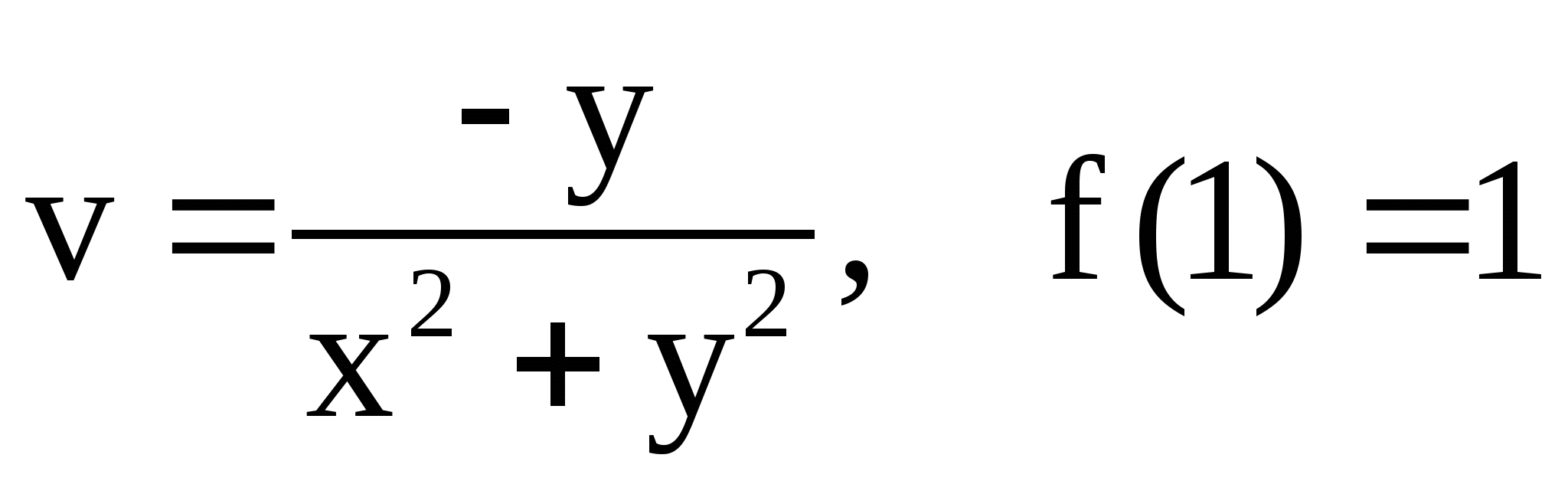 ;
;
18. ![]() ;
;
19. ![]() ;
;
20. ![]() ;
;
21. 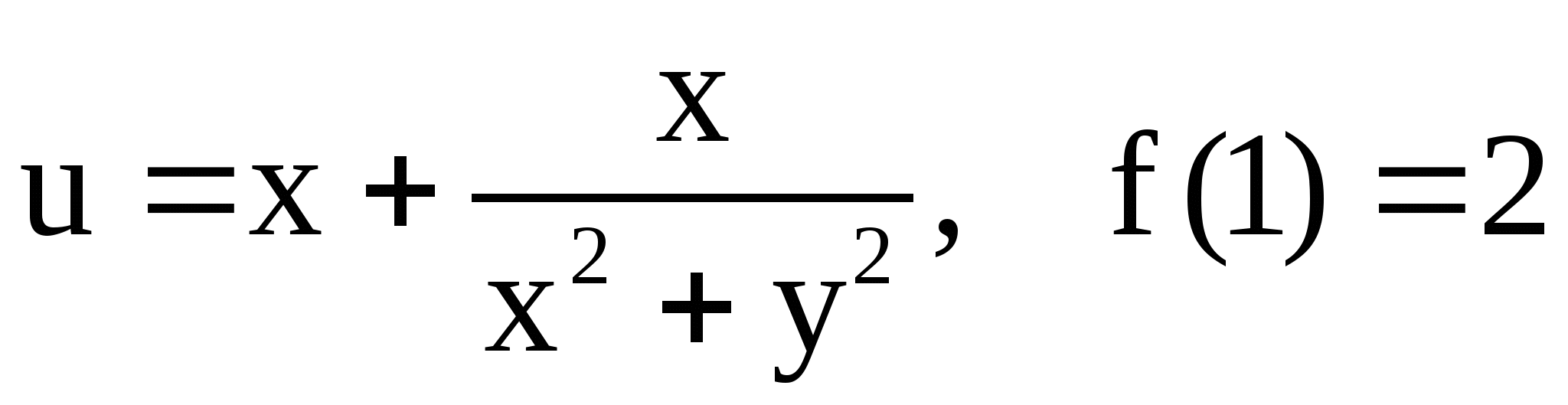 ;
;
22. ![]() ;
;
23. ![]()
![]() ;
;
24. ![]() ;
;
25. ![]() ;
;
26. ![]() ;
;
27. ![]() ;
;
28. ![]() ;
;
29. ![]() ;
;
30. ![]() .
.
Литература
1. Арамович И. Г., Лунц Г. Л., Эльсгольц Л. Э. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. М.: Наука, 1968. 41 с.
2. Бугров Я. С., Никольский С. М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М.: Наука, 19685. 464 с.
3. Ефимов А. В. Математический анализ (специальные разделы). Общие функциональные ряды и их приложение. М.: Высш. школа, 1980. 279 с.
4. Краснов М. Л., Киселев А. И., Макаренко Г. И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. М.: Наука, 1981. 302 с.
5. Лаврентьев М. А., Шабаш Б. В. Методы теории функций комплексного переменного. М.: Наука, 1973. 736 с.
6. Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной. М.: Наука, 1979. 320 с.
7. Веснина А.А. Хаустова Н.М. Теория функций комплексной переменной. // Омск.- Методические указания, ОмГТУ.- 2005.- 68С.
Содержание
§1.1 Комплексные числа и действия над ними 3
§1.2 Алгебраические действия над комплексными числам 5
§1.3 Понятие функции комплексного переменного. Элементарные функции 8
§1.4 Задачи 13
§1.5 Задачи для самостоятельного решения 13
§2.1 Производная функции комплексного переменного 14
§2.2 Задачи 18
§2.3 Задачи для самостоятельного решения 19
§3.1 Ответы на задачи для самостоятельного решения 19
§4.1 Задачи контрольной работы 23
Литература 29
Содержание 30</</font>