- Учителю
- методическая разработка урока математики в 11 классе с презентацией
методическая разработка урока математики в 11 классе с презентацией





Муниципальное бюджетное образовательное учреждение
«Средняя школа №6» города Смоленска
Методическая разработка
Конспект урока по математике
в 11 классе
Определение логарифма
Подготовила
учитель математики
Хатрусова Раиса Дмитриевна
Смоленск 2015
Тема урока: Определение логарифма числа. Свойства логарифмов.
Девиз урока:
Умение мыслить математически - одна из благороднейших способностей человека.
Б.Шоу
Тип урока: Изучение нового материала.
Цели урока:
Обучающая:
- ввести понятие логарифма числа;
- сформировать понятие о свойствах логарифма;
- научить преобразовывать выражения, содержащие логарифмы.
Развивающая:
- способствовать развитию логического мышления при изучении темы «Логарифм числа»;
- способствовать развитию умения прогнозировать, лаконично и математически грамотно выражать свои мысли;
- способствовать развитию умений осуществлять самоконтроль и самооценку.
Воспитательная:
- способствовать воспитанию целеустремленности, настойчивости в достижении цели, эстетического наслаждения от решенной задачи;
- способствовать воспитанию активности, мобильности, толерантности.
Средства обучения: компьютер, проектор, презентация, письменные принадлежности.
План урока:
-
Организационный момент.
-
Актуализация опорных знаний учащихся.
-
Изучение нового материала и первичное закрепление изученного материала.
-
Закрепление усвоенных знаний.
-
Домашнее задание.
-
Рефлексия.
Ход урока:
-
Организационный момент.
-
Актуализация опорных знаний
Ученикам предлагается решить 3 простейших показательных уравнения:
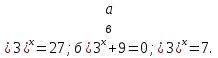
Ответы: а) 3; б) нет корней; в) ? .
При решении уравнения в) 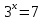 у учащихся возникают трудности, им не хватает для решения знаний.
у учащихся возникают трудности, им не хватает для решения знаний.
Возникла проблема 1: имеет ли уравнение корни, и если имеет, то как решить уравнение?
-
Изучение нового материала. Первичное закрепление изученного материала.
-
Рассмотрим графический способ решения уравнения в).
-
у y 
7
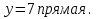
1
х
Итак, получаем первый вывод: корень уравнения существует, корнем уравнения является абсцисса точки пересечения графиков функций.
Проблема 2: как записать корень уравнения?
Рассмотрим новую форму записи корня данного уравнения.
Введем символическую запись корня в виде логарифма:  .
.
В рассматриваемом уравнении х =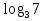
Затем вводится определение логарифма числа:
Логарифмом положительного числа b по положительному и отличному от 1 основанию а называют показатель степени, в которую нужно возвести число а, чтобы получить число b.
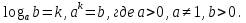
Термин «Логарифм» предложил Джон Непер - шотландский математик
(1550-1617). От греческого logos - число, arithmos - отношение.
Операция нахождения логарифма числа обычно называется логарифмированием.
Это обратная операция возведению в степень с соответствующим основанием.
Примеры. 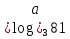 =4, так как
=4, так как 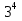 =81; б)
=81; б)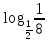 = 3, так как
= 3, так как 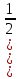 .
.
-
-
Самостоятельная работа обучающего характера:
-
А) Запишите в виде степени 


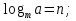
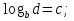 .
.
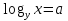 :
:
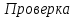
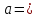
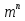
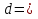
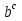
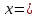
Б) Запишите в виде логарифма
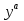 ;
; 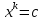 ;
;
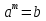
Проверка:
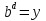
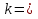
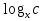
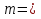
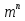
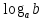
-
-
Упражнения на вычисление логарифма по определению.
-
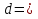
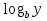
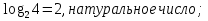
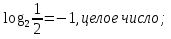
Получаем второй вывод о том, что значение логарифма - действительное число.
-
-
Первичное закрепление нового материала.
-
Условие. Вам предлагается три задания.
Необходимо назвать, чему равны неизвестные компоненты, обозначенные *.
Записать вместо * числа. Сделать выводы по каждому виду заданий.
№1:
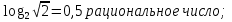 * , 2* = 8
* , 2* = 8
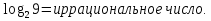 ,
, 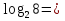 = *
= *
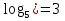 , 91 = *
, 91 = *
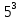 , 3-3 = *
, 3-3 = *
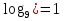 ,
, 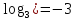 = 256
= 256
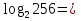 *,
*, 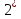 =
= 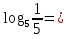
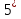 , 41 = *
, 41 = *
Вывод: по определению логарифма
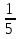 ах = b при a > 0, a ≠ 1, b > 0.
ах = b при a > 0, a ≠ 1, b > 0.
№2:
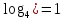 * ,
* , 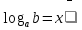 = 1
= 1
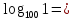 ,
, 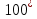 = 1
= 1
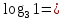 , 20 = *
, 20 = *
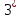 0 ,
0 , 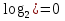 = 1
= 1
Вывод: 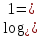 , т.к. а0 = 1 при a > 0, a ≠ 1.
, т.к. а0 = 1 при a > 0, a ≠ 1.
№3:
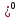 , 51 = *
, 51 = *
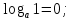 ,
, 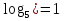 = 20
= 20
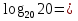 , 71 = *
, 71 = *
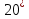 ,
, 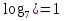 = 8
= 8
Вывод: 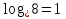 т.к. а1 = а при a > 0, a ≠ 1.
т.к. а1 = а при a > 0, a ≠ 1.
-
-
Простейшие свойства логарифма.
-
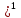
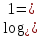
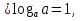 .
.
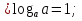
-
-
Обращение к учебнику (А.Г.Мордкович «Алгебра и начала математического анализа» 10-11 класс, базовый уровень, стр. 280, вопросы для самопроверки).
-
-
Закрепление усвоенных знаний.
4.1. Обучающая самостоятельная работа на применение определения логарифма и простейших свойств. Работа в парах с последующей проверкой.
№
задания
Примеры
ответы
1
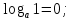
1
2
11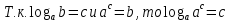
11
3
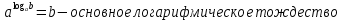
0
4
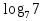
3
5
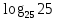
11
6
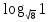
6
4.2. Решение упражнений из задачника: п.41, №№ 41.3-41.6; 41.7-41.9(а, б).
-
Домашнее задание. П.41, №№ 41.7-41.9 (в,г); 41.15.
-
Подведение итогов. Рефлексия.
Учащимся предлагается дать оценку уровня усвоения нового материала на уроке, ответив на вопросы:
-
Я усвоил тему …
-
Я понял, что недостаточно усвоил, но смогу дома разобраться самостоятельно …
-
Я понял, что не усвоил тему, обращусь за помощью к учителю…
Заключительное слово учителя:
Обращаю внимание учащихся на слова М.И.Калинина, актуальные в современное время:
"Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе".
Спасибо за урок!