- Учителю
- Проверочная работа Перпендикуляр к плоскости.
Проверочная работа Перпендикуляр к плоскости.
Автор публикации: Останина Е.П.
Дата публикации: 06.12.2016
Краткое описание:
предварительный просмотр материала
|
</Вариант
-
Длина стороны ромба ABCD равна 5 см, длина диагонали
BD равна 6 см. Через точку О пересечения диагоналей ромба
проведена прямая ОК, перпендикулярная его плоскости.
Найдите расстояние от точки К до вершин ромба, если ОК =
8 см.
-
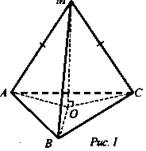
Дано: ΔАВС - правильный; АВ = 6 см; М ∉ (ABC); АМ = ВМ
= СМ = 4 см. Найти: расстояние от М до (ABC).
-
Дано: ABCD -ромб, AC ∩ BD =О, OK ⊥ (ABC), AC ⊥
BD.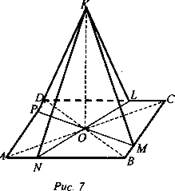
Доказать: КМ = KN = КР = KL, то есть О - центр вписанной в
ромб окружности.
|
Вариант
-
Длины сторон прямоугольника равны 8 и 6 см. Через
точку О пересечения его диагоналей проведена прямая ОК,
перпендикулярная его плоскости. Найдите расстояние от
точки К до вершин прямоугольника, если ОК = 12 см.
-
Дано: ABCD - тетраэдр, М - середина ВС, АВ = AC; DB =
DC . Доказать: ВС ⊥ (ADM).
3.Дано:ABCD прямоугольник; АК ⊥ (ABC); KD = 6 см, KB = 7
см, КС = 9 см. Найти: Расстояние (К; (ABC)); 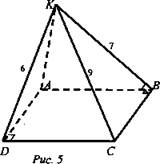 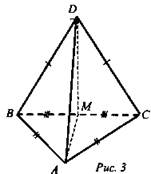
|
|
|
|
|
Вариант
-
Длина стороны ромба ABCD равна 5 см, длина диагонали
BD равна 6 см. Через точку О пересечения диагоналей ромба
проведена прямая ОК, перпендикулярная его плоскости.
Найдите расстояние от точки К до вершин ромба, если ОК =
8 см.
-
Дано: ΔАВС - правильный; АВ = 6 см; М ∉ (ABC); АМ = ВМ
= СМ = 4 см. Найти: расстояние от М до (ABC).
-
Дано: ABCD -ромб, AC ∩ BD =О, OK ⊥ (ABC), AC ⊥
BD.
Доказать: КМ = KN = КР = KL, то есть О - центр вписанной в
ромб окружности.

|
Вариант
-
Длины сторон прямоугольника равны 8 и 6 см. Через
точку О пересечения его диагоналей проведена прямая ОК,
перпендикулярная его плоскости. Найдите расстояние от
точки К до вершин прямоугольника, если ОК = 12 см.
-
Дано: ABCD - тетраэдр, М - середина ВС, АВ = AC; DB =
DC . Доказать: ВС ⊥ (ADM).
3.Дано:ABCD прямоугольник; АК ⊥ (ABC); KD = 6 см, KB = 7
см, КС = 9 см. Найти: Расстояние (К; (ABC));  
|
|
|
|



