- Учителю
- Урок по математике на тему «Свойства степени с целым показателем»
Урок по математике на тему «Свойства степени с целым показателем»
Свойства степени с целым показателем
Цель: изучение свойства степени с целым показателем и их использование при решении задач.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
III. Изучение нового материала (основные понятия)
Наводящими вопросами (путем фронтального опроса) подведите учащихся к изучению этой темы. Для этого:
1. Попросите сформулировать свойства степени с натуральным показателем (вспомнить материал 7-го класса).
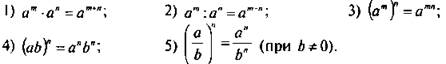
2. На примерах предложите проверить, выполняются ли эти свойства в случае отрицательных целых показателей степени (с очевидным ограничением а ≠ 0, b ≠ 0).
Пример 1
![]() (свойство 1).
(свойство 1).
![]() (свойство 4).
(свойство 4).
На основании этих примеров можно высказать гипотезу, что свойства 1-5 выполняются и в случае степени с целым отрицательным показателем.
3. Предложите учащимся доказать, например, свойства 1 и 4 в случае степени с целым отрицательным показателем.
Пример 2
Докажем свойство 1, т. е. ![]() (где m и n - целые отрицательные числа, а - любое число (а ≠ 0)).
(где m и n - целые отрицательные числа, а - любое число (а ≠ 0)).
По определению степени с целым отрицательным
показателем запишем ![]() Числа (-m) и (-n) являются уже натуральными. Поэтому по свойству
степеней с натуральными показателями получаем:
Числа (-m) и (-n) являются уже натуральными. Поэтому по свойству
степеней с натуральными показателями получаем: ![]() На заключительном этапе вновь было использовано определение
степени с целым отрицательным показателем.
На заключительном этапе вновь было использовано определение
степени с целым отрицательным показателем.
Пример 3
Докажем свойство 4, т. е. ![]() (где n - целое отрицательное число, а и b - любые числа (а ≠ 0, b
≠ 0).
(где n - целое отрицательное число, а и b - любые числа (а ≠ 0, b
≠ 0).
По определению степени с целым отрицательным
показателем запишем ![]() Число (-n) будет уже натуральным. По свойству степеней с
натуральными показателями имеем:
Число (-n) будет уже натуральным. По свойству степеней с
натуральными показателями имеем: ![]()
![]() В конце снова было использовано определение степени с целым
отрицательным показателем.
В конце снова было использовано определение степени с целым
отрицательным показателем.
Таким образом, свойства 1-5 (для натуральных показателей степени) можно обобщить и на случай целых отрицательных показателей степени.
Пример
Преобразуем выражения: 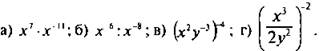
а) Учтем, что при умножении чисел с одинаковыми
основаниями показатели степеней складываются. Получаем: ![]()
б) При делении чисел с одинаковыми основаниями
показатели степеней вычитаются. Имеем: ![]()
в) При возведении в степень произведения
возводят в эту степень каждый множитель и результаты перемножают.
При возведении степени в степень основание оставляют прежним, а
показатели перемножают. Получаем: ![]()
г) При возведении в степень дроби возводят в эту
степень ее числитель и знаменатель и результаты делят. При
возведении степени в степень основание оставляют прежним, а
показатели перемножают. Имеем: ![]()
Упомянутые свойства степеней используются и при решении более сложных задач.
V. Задание на уроке
№ 926 (а, г, д); 932 (а, в); 935 (д); 937; 939 (б); 940; 945 (а, г); 947 (а, в).
VI. Задание на дом
№ 926 (б, в, е); 932 (б, г); 935 (е); 936; 939 (д); 941; 945 (б, в); 947 (б, г).
</ VII. Подведение итогов урока