- Учителю
- План - конспект урока в 11 классе по алгебре и началам анализа «Применение производной для исследования функций на монотонность»
План - конспект урока в 11 классе по алгебре и началам анализа «Применение производной для исследования функций на монотонность»
План -конспект урока алгебры и начала анализа в 11 классе МБОУ «СОШ №3»
с использованием здоровьесберегающих технологий
Учитель: Ивченко И.Ю.
Дата: 13марта 2013 г.
Тема : «Применение производной для исследования функций на монотонность»
Тип урока урок разноуровневого обобщающего повторения
Урок составлен для учащихся общеобразовательного 11 класса.
Цель урока. Обобщить теоретические знания по теме « Применение производной для исследования функций на монотонность». Рассмотреть методы решения заданий базового и повышенного уровня сложности на данную тему. Организовать работу учащихся по указанной теме на уровне, соответствующем уровню уже сформированных знаний.
Оборудование.
-
Интерактивная доска. На уроке используются презентация « Применение производной для исследование функций на монотонность»
-
При повторении теоретического материала на доске высвечиваются тестовые задания, используемые в ЕГЭ, с выбором ответа и демонстрируется правильный ответ, что позволяет учащемуся наглядно представить смысл задания.
2.Раздаточный материал, подготовленный учителем для организации самостоятельной работы.
Ход урока:
I этап урока - организационный (1 минута)
Учитель сообщает учащимся тему урока, цель и поясняет, что во время урока постепенно будет использоваться тот раздаточный материал, который находится на столах.
II этап урока (2 минуты) - Актуализация знаний учащихся
Учитель обращается к детям с вопросом: «Какая существует связь между характером монотонности функции и знаком её производной?».
Ответ учеников может быть таким: «Если функция возрастает на промежутке и имеет на нём производную, то производная неотрицательна; если функция убывает на промежутке и имеет на нём производную, то производная неположительна.»
Учитель: « Сформулируйте признаки монотонности функции»
Ответ может быть таким: «1. Если во всех точках открытого промежутка Х выполняется неравенство f1(x)![]() 0 (причём равенство f1(x)=0 выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция у=f(x) возрастает на промежутке Х.
0 (причём равенство f1(x)=0 выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция у=f(x) возрастает на промежутке Х.
2. Если во всех точках открытого промежутка Х выполняется неравенство f1(x)![]() 0 (причём равенство f1(x)=0 выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция у=f(x) убывает на промежутке Х.»( учебник А.Г.Мордкович)
0 (причём равенство f1(x)=0 выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция у=f(x) убывает на промежутке Х.»( учебник А.Г.Мордкович)
III этап - Работа с тренажёром. (10 минут)
Учащиеся берут на своих столах тематический тренажёр с заданиями ЕГЭ. Задания выполняются самостоятельно, проводится взаимопроверка по готовым ответам (ответы можно заготовить на слайде интерактивной доски с занавеской), разбираются задания, вызвавшие затруднения. (Наиболее подготовленным учащимся, справившимся с заданиями тренажёра №1, можно предложить более сложные задания тренажёра №2)( см. приложение ниже)
Ответы на тренажёр №1
-
1
2
3
4
5
6
7
8
9
10
-1,5
3
0
-1
2
-0,5
1,5
0
-1,5
0,75
Ответы на тренажёр №2
-
№
1
2
3
4
5
6
7
8
ответ
-2
5
5
3
2
4
1,5
5
IV этап - Работа по теме урока. (15 минут)
(Задания записаны на страничках интерактивной доски, ниже учащиеся приводят решения)
Слайд №1 Исследовать на монотонность функцию у = х5 + х3 +1.
Решение:
D(y) = R; у'=5х4 + 3х2
Справедливо неравенство 5х4 + 3х2 ![]() 0
0
Нули производной: 5х4 +3х2 =0,
х2(5х2 +3)=0,
х=0 , 5х2 +3=0 - нет решений
f'(x) + +
_________________________________
f(x) 0
y'>0 и функция у = х5 + х3 +1 возрастает на всей числовой прямой.
Слайд 2. Исследовать на монотонность функцию y = 2 sinx -3x.
Решение:
D(y) = R; Имеем у' = 2 cosx - 3, т.к. | cosx| ![]() 1, то 2 cosx - 3 <0 при всех х. Значит y'< 0. Функция y = 2 sinx -3x убывает на всей числовой прямой.
1, то 2 cosx - 3 <0 при всех х. Значит y'< 0. Функция y = 2 sinx -3x убывает на всей числовой прямой.
Слайд 3. Работа по учебнику (Мордкович А.Г., стр 97)
( у доски 3 человека слабый-средний-сильный, остальные работают в тетрадях)
№ 30.14( в) Исследовать на монотонность функцию у= -3х4 +4х3 -15
№ 30.15( в) Исследовать на монотонность функцию ![]() .
.
№ 31.5( а) Исследовать на монотонность функцию у = х3 - 3х + 2 и построить схематически её график.
Физминутка (с помощью офтальмотренажёра)
Упражнение по профилактике нарушения зрения
1) вертикальные движения глаз вверх - вниз;
2) горизонтальное вправо - влево;
3) вращение глазами по часовой стрелке и против;
4) закрыть глаза и представить по очереди цвета радуги как можно отчетливее;
5) с помощью офтальмотренажёра предлагается глазами «нарисовать» одну из понравившихся фигур несколько раз в одном, а затем в другом направлении.
V этап Cамостоятельная работа (дифференцируемая: для слабых варианты 1,2, для более подготовленных детей варианты 3,4)
С.Р. ВАРИАНТ 1 11 кл.
-
Найдите промежутки возрастания и убывания функции: а) f(x) = х2 + 3х + 6;
б) g (x) = 3x3 - x2 - 7x;
в) h (x) = sin 3x - 4x.
2. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.
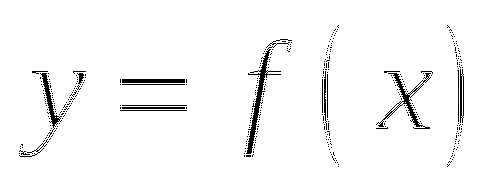 3. На рисунке изображен график функции
3. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.
С.Р. ВАРИАНТ 2 11 кл.
1.Найдите промежутки возрастания и убывания функции: а) f(x) = - х2 + 4х - 3;
б) g (x) = 2x3 + 3x2 - 12x;
в) h (x) = cos 2x + 3x.
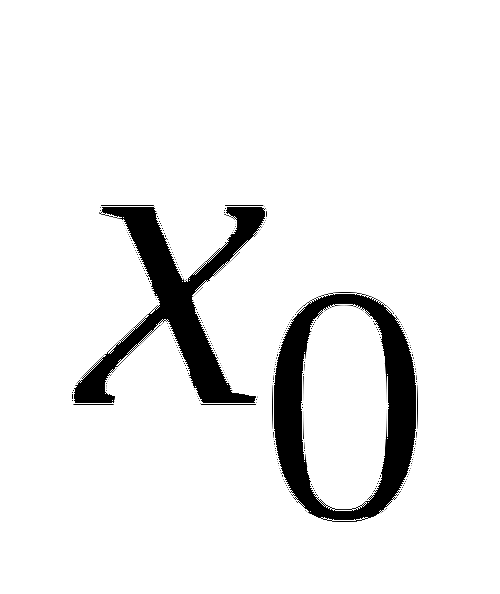 2. На рисунке изображен график функции
2. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.
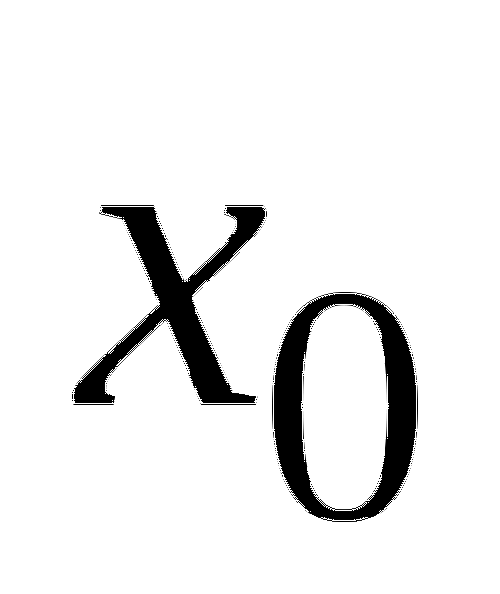
3. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.
С.Р. ВАРИАНТ 3 11 кл.
-
Исследуйте функцию на монотонность:
а) ![]() ;
;
б) y = sinx - 3x.
2. При каких значениях параметра p функция ![]()
возрастает на всей числовой прямой?
С.Р. ВАРИАНТ 4 11 кл.
-
Исследуйте функцию на монотонность:
а) ![]() ;
;
б) у = сosx +5x.
2. При каких значениях параметра p функция ![]() убывает на всей числовой прямой?
убывает на всей числовой прямой?
VI этап Итоги урока.
Домашнее задание №30.14 а, 30.15 а, 31.5 б, ( + обменяться вариантами с.р.)
ПРИЛОЖЕНИЕ( к уроку «Применение производной для исследования функций на монотонность»
Тренажёр №1
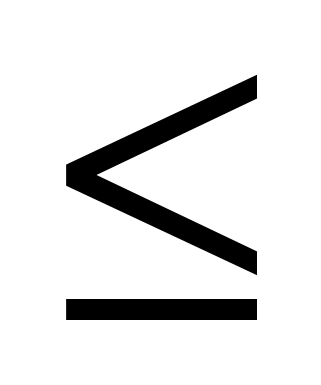
1. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.
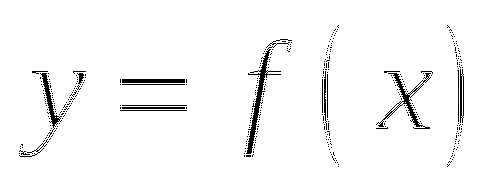 2. На рисунке изображен график функции
2. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.
 3. На рисунке изображен график функции
3. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.
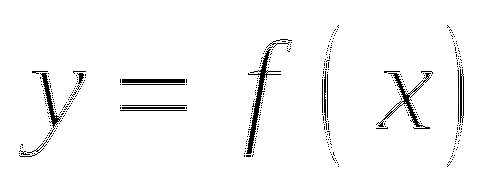 4. На рисунке изображен график функции
4. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.
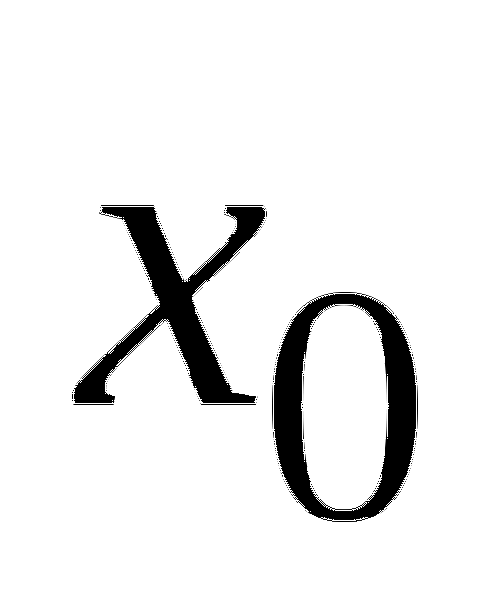
5. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.
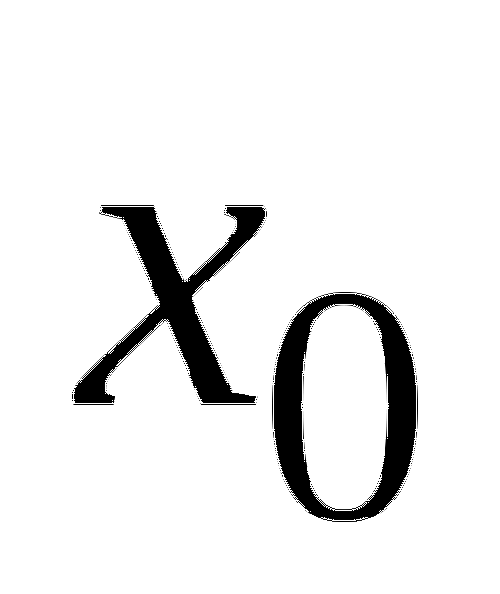
6. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.
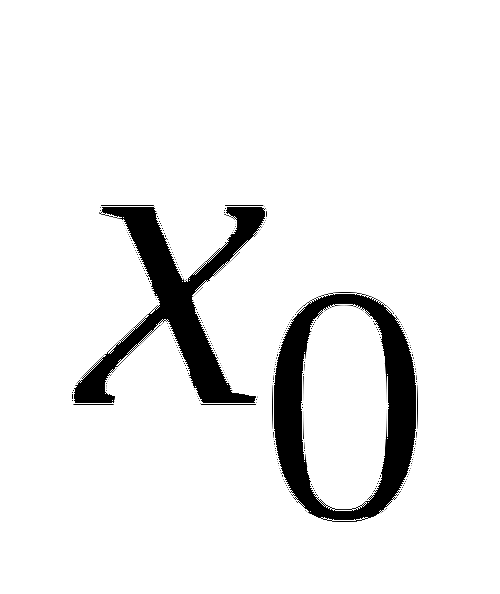 7. На рисунке изображен график функции
7. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.
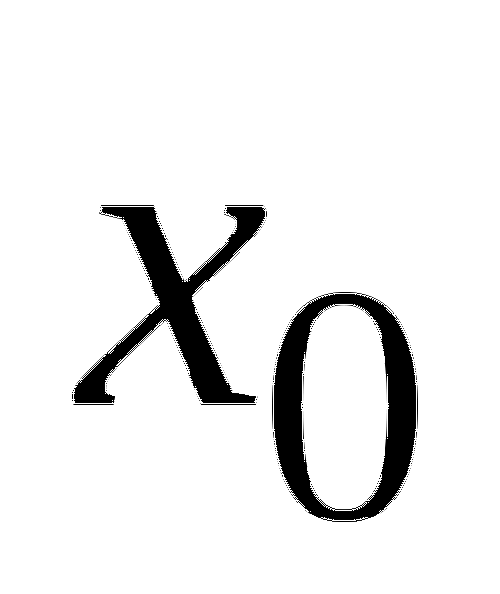 8. На рисунке изображен график функции
8. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.
 9. На рисунке изображен график функции
9. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.
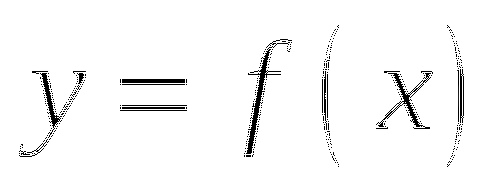 10. На рисунке изображен график функции
10. На рисунке изображен график функции ![]() и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой ![]() . Найдите значение производной в точке
. Найдите значение производной в точке ![]() .
.
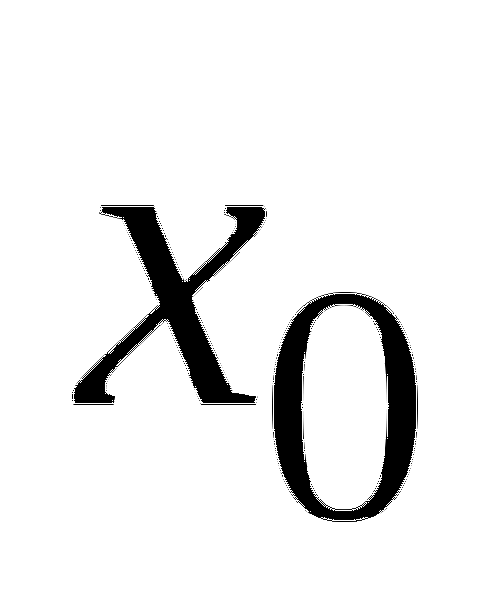 Тренажёр №2
Тренажёр №2
1. Функция ![]() определена на промежутке
определена на промежутке ![]() . На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции
. На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции ![]() имеет наибольший угловой коэффициент.
имеет наибольший угловой коэффициент.
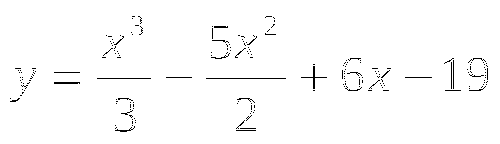 2. Функция
2. Функция ![]() определена на промежутке
определена на промежутке ![]() . На рисунке изображен график производной этой функции.
. На рисунке изображен график производной этой функции.
К графику функции провели касательные во всех точках, абсциссы которых целые числа. Укажите количество точек графика функции, в которых проведенные касательные имеют отрицательный угловой коэффициент.
3. Прямая пересекает ось абсцисс при ![]() , касается графика функции
, касается графика функции ![]() в точке
в точке ![]() . Найдите
. Найдите ![]() .
.
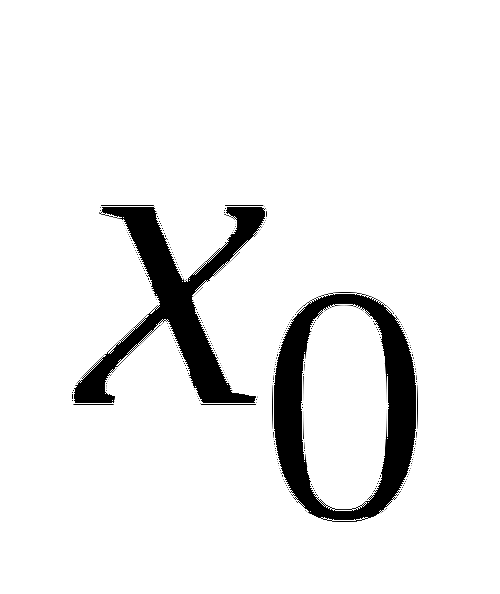
4. Функция ![]() определена на промежутке
определена на промежутке ![]() . Используя изображенный на рисунке график производной
. Используя изображенный на рисунке график производной ![]() , определите количество касательных к графику функции
, определите количество касательных к графику функции ![]() , которые составляют угол
, которые составляют угол ![]() с положительным направлением оси Ox.
с положительным направлением оси Ox.
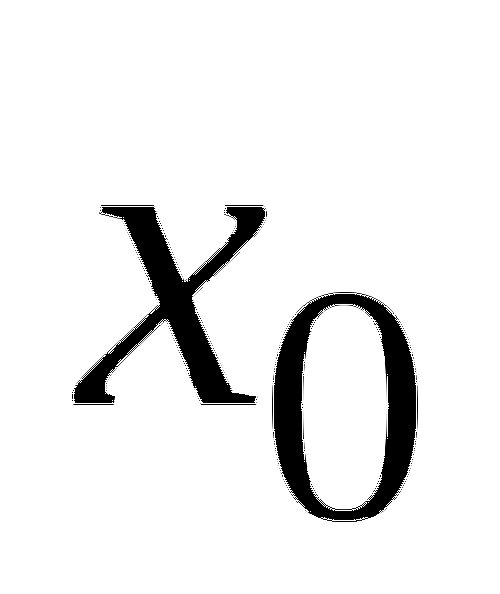 5. Функция
5. Функция ![]() определена на промежутке
определена на промежутке ![]() . На рисунке изображен график производной этой функции.
. На рисунке изображен график производной этой функции.
К графику функции провели касательные во всех точках, абсциссы которых целые числа. Укажите количество точек графика функции, в которых проведенные касательные имеют отрицательный угловой коэффициент.
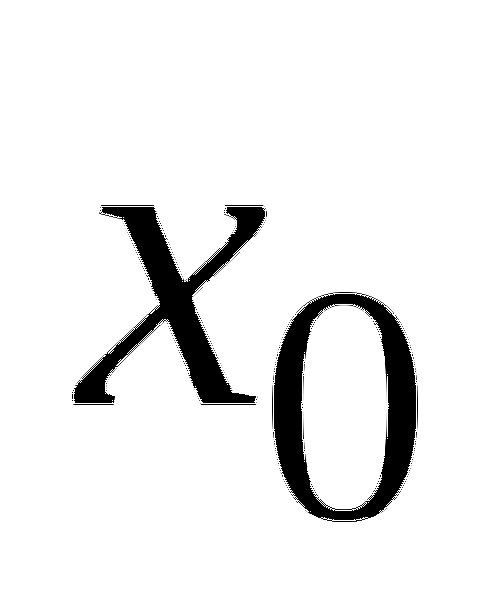
6. Функция ![]() определена на промежутке
определена на промежутке ![]() . На рисунке изображен график производной
. На рисунке изображен график производной ![]() . Определите число касательных к графику функции
. Определите число касательных к графику функции ![]() , тангенс угла наклона которых к положительному направлению оси Ox равен 3.
, тангенс угла наклона которых к положительному направлению оси Ox равен 3.
7. Прямая пересекает ось ординат при ![]() , касается графика функции
, касается графика функции ![]() в точке
в точке ![]() . Найдите
. Найдите ![]() .
.
 8. Функция
8. Функция ![]() определена на промежутке
определена на промежутке ![]() . На рисунке изображен график производной этой функции.
. На рисунке изображен график производной этой функции.
К графику функции провели касательные во всех точках, абсциссы которых целые числа. Укажите количество точек графика функции, в которых проведенные касательные имеют отрицательный угловой коэффициент.