Конспект урока для 11 класса «Подготовка к ЕГЭ. Тригонометрические формулы»

Тригонометрические формулы.

Цель урока:

• обобщить и систематизировать знания по теме «Тригонометрические формулы»;

• подготовиться к ЕГЭ;

• проверить уровень усвоения темы.

Задачи урока:

• повторить определение синуса, косинуса, тангенса, котангенса числа α;

• повторить основное тригонометрическое тождество и формулы, выражающие связь между тангенсом и косинусом, между котангенсом и синусом, формулы приведения, формулы двойного угла;

• научить применять полученные знания при решении задач.

Ход урока:

1.О.Н.У.

Угадайте тему, о чем пойдет речь на уроке. Сл №1

Историки полагают, что тригонометрию создали древние астрономы, немного позднее её стали использовать в геодезии и архитектуре. Со временем область применения тригонометрии постоянно расширялась, в наши дни она включает практически все естественные науки, технику и ряд других областей деятельности. Томас Пейн в своей книге «Век Разума» (1794) назвал тригонометрию «душой науки».

А в заданиях ЕГЭ есть тригонометрия? В каких?

Запишите число, классная работа и тему урока. Сл № 2

Как вы думаете, какова цель нашего урока? Сл №3

С учетом цели, какие задачи мы должны поставить перед собой на этом уроке? Сл №4

2. Устная работа.

1) Вспомним определение тригонометрических функций и ряд основных формул. Сл №5

Синусом угла α называется _____ точки, полученной поворотом точки______

вокруг начала координат на угол α

tg α =

sin² α +cos² α=

1+ tg² α=

sin(-α)=

tg (-α) =

sin 2α=

Косинусом угла α называется _____ точки, полученной поворотом точки______ вокруг начала координат на угол α

ctg α=

tg α∙ ctg α=

1+ ctg² α=

cos (-α)=

ctg (-α) =

cos 2α=

2)Отметьте знаки тригонометрических функций. Сл №6

3) И наконец, формулы приведения. Их много, можно все не запомнить. Но есть правило приведения, с помощью которого можно вывести все формулы. Вспомним. (дети проговаривают правило)

Применение формул приведения можно свести к использованию правила:

1) если в формуле содержатся углы 180° и 360° (π и 2π), то наименование функции не изменяется;

если же в формуле содержатся углы 90° и 270° (π/2 и 3π/2), то наименование функции меняется на сходное (синус на косинус, тангенс на котангенс и т. д.);

2) чтобы определить знак в правой части формулы (+ или-), достаточно, считая угол φ острым, определить знак выражения, стоящего в левой части формулы.

Сл №7 Несколько вывести формул на доске с учащимися используя правило на слайде.

3. Практическая часть урока.

1) Сл №8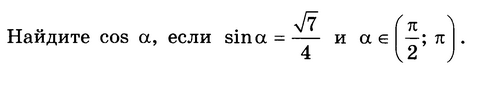

2) Сл №9

3) Правило запоминания значений синуса и косинуса по руке. Несколько примеров, отработать прием. Сл №10 Сл №11

4) Сл №12 Найдите значение выражения

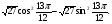5) Сл № 13 Найдите значение выражения

6) Сл № 14 Найдите значение выражения

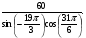
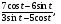7) Сл № 15 Найдите значение выражения

8) Сл № 16 Найдите если tg t = 1.

4. Самостоятельная работа

Прототип В-7. Тригонометрия

Вариант 1

1. Найдите tg , если sin 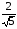 = - и   (; 1,5).

2. Найдите 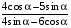, если tg  = 1.

3. Найдите значение выражения .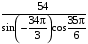

_______________________________________________________________

Самостоятельная работа

Прототип В-7. Тригонометрия

Вариант 2

1. Найдите cos , если sin 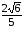 = - и   (; 1,5).

2. Найдите 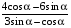, если tg  = 3.

3. Найдите значение выражения .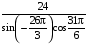

5. Рефлексия.

Вспомните, какие цели и задачи были поставлены в начале урока. Как вы думаете, мы достигли их. Оцените свои результаты смайликами на интерактивной доске.

6. Домашнее задание:

№ 458

электронный дневник- задание В7 вариант №1-5