Конспект урока по математике на тему ' Конус. Практическ5ое применение'.

Урок геометрии в 11 классе.

Тема: « Конус. Практическое применение».

Учитель: Григорьева Алина Борисовна.

«Изучение геометрии без должной связи с жизнью, без наглядности мешает развитию логического мышления, снижает уровень математической подготовки учащихся».

А.И.Маршукевич.

ЦЕЛЬ УРОКА: Систематизация и углубление знаний по теме "Конус". Повысить интерес к геометрии, решая нестандартные задачи. Создание положительной внутренней мотивации обучения учащихся.

• Образовательная:

  • отрабатывать знания основных понятий, определений, теорем и умения применять эти знания при решении задач различных по содержанию и уровню сложности.

• Развивающая:

  • развивать логическое мышление, умение сравнивать, обобщать, классифицировать;

  • развивать и совершенствовать умения применять накопленные знания в измененной ситуации, делать выводы и обобщения.

  • развитие навыков работы с различными по жанру текстами, умения «отсеивать» лишние факты, переводить жизненные задачи на язык математики.

• Воспитательная:

  • воспитывать ответственность за результат своего труда.

  • повышение общекультурного уровня учащихся,

  • развитие навыка работы в группе.

ЗАДАЧИ УРОКА:

• развивать пространственное воображение учащихся;

• способствовать развитию логического мышления при решении задач;

• показать связь теории с практикой.

ОБОРУДОВАНИЕ:

• мультимедийный проектор;

• компьютер;

• экран;

• раздаточный материал;

• калькулятор.

Ход урока.

I. Организационный момент.

(слайд 1,2)

Объявляется тема, цель урока. Задаётся домашнее задание "Проекты - победители". Учащиеся получают задание по группам.

ДОМАШНЕЕ ЗАДАНИЕ:

Детский спортивно-развлекательный комплекс, который начали строить несколько лет назад, должен принять первых посетителей в ближайшие зимние каникулы. Отделочные работы уже закончены. Осталась башня - украшение крыши. В сентябре был объявлен конкурс на лучший проект этого сооружения. Планируется изготовить его из оцинкованного железа. Комиссия выбрала два чертежа и представила их на рассмотрение губернатору города. Представьте, что вы члены комиссии и выберите, пожалуйста, экономически выгодный проект башни.

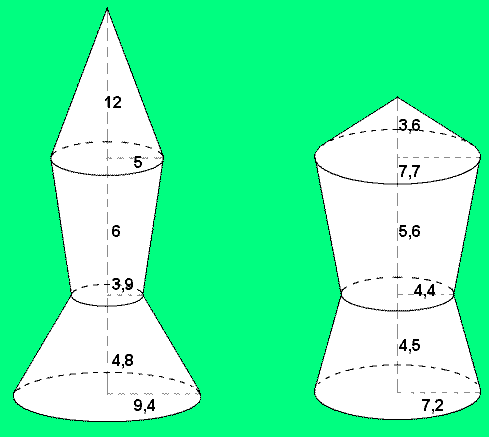
Прайс-лист хозяйственного магазина "Мой дом".

II. Актуализация знаний учащихся класса.

1). Сегодня на уроке мы обобщим и систематизируем свои знания по теме "Конус", повторим основные формулы и применим их при решении практических задач.

Вы должны были повторить основные понятия по теме и установить связь между картиной Шишкина "Корабельная роща" и геометрическим телом, которое называется "конус". Кто из Вас нашел эту "связь"? (Учитель демонстрирует репродукцию картины: слайд 3).

Ответ: Конус в переводе с греческого языка означает "сосновая шишка", а на картине изображен сосновый лес.

2). Графический диктант (слайды 4-7).

III. Презентация учащихся "Конусы в нашей жизни".

Как вы сейчас узнали, конус очень часто можно встретить в настоящей жизни. А теперь нам предстоит решить задачи с практическим применением теоретических знаний.

IV. Применение полученных знаний при решении практических задач.

Задача № 1. (слайды 8) "Колпак для клоуна".

Колпак к костюму клоуна имеет вид конуса, радиус основания которого равен 8 см, а высота колпака 12 см. Сколько метров ткани надо купить, чтобы обтянуть этот колпак?

Решение:

Sб= π * R * L

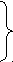по теореме Пифагора: L=√ 144+64=√208≈14,4 см;

π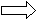 ≈ 3,14,

R=8 см

Sб= 3,14*8*14,4=25,12*14,4

25,12 см ≈ 0,25 м длина ткани; 14,4 см ≈ 0,14 м ширина ткани

Ответ: 0,25 м ткани надо купить

Задача № 2. (слайды 9,10) "Молниеотвод".

Большую угрозу для жизни и деятельности человека представляют разряды молнии. Защитить жилье и производственные объекты помогают молниеотводы. Громоотводами их назвали тогда, когда еще не было дано научного объяснения грозе, как природному явлению. По статистике на Земле ежегодно гибнет от разрядов молний 6 человек на 1 000 000 жителей (чаще в южных странах). Этого бы не случалось, если бы везде были громоотводы, так как образуется конус безопасности. Чем выше громоотвод, тем больше объем такого конуса. Некоторые люди пытаются спрятаться от разрядов под деревом, но дерево не проводник, на нем заряды накапливаются, и дерево может быть источником напряжения.

Условие задачи :

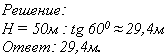Вычислите высоту молниеотвода, если радиус "защищенного" круга 50 м, а угол между молниеотводом и образующей конуса безопасности 60⁰ (самостоятельная работа на местах с последующей проверкой).

Задача № 3. (слайд 12,13) "Плювиограф".

Для сбора и ежедневного замера дождевых осадков служат плювиографы. Снег и град растапливают для получения водного эквивалента. Рассмотрим прибор для измерения осадков. Его основные части - это знакомые вам тела вращения (рассмотреть, обсудить).

Определить по имеющимся данным количество материала, необходимого для изготовления воронки прибора, с учётом того, что на подгибку и заклёпку необходимо добавить 5%.

(слайд 14)

Задача № 3. (слайд 15) "Вольный воздух".

Вы уже знаете, как найти элементы конуса, его поверхность, но сможете ли Вы применить свои знания, выходя на "вольный воздух". Ведь куча щебня по краям шоссейной дороги также представляет предмет, заслуживающий внимания. Посмотрев на неё, мы можем задать себе вопросы:

• Какую площадь занимает щебень?

• Какова поверхность этой кучи щебня?

• Каков объём?

Задачи довольно сложные для человека, привыкшего преодолевать математические трудности только на бумаге или на классной доске. Ведь необходимо вычислить поверхность конуса, высота и радиус которого не доступны для непосредственного измерения. Вопросы к классу:

Как найти радиус?

(измерить окружность основания и разделить на 6,28 = 2π);

Как найти образующую?

(определить две образующие: перекинув рулетку (верёвку) через вершину кучи):

Как найти высоту?

(определить по теореме Пифагора).

Условие задачи (слайд 16):

Пусть окружность конической кучи щебня 12 м. Длина двух образующих - 4,6 м.

Найти площадь поверхности кучи щебня.

Решение.

L= 4,6 : 2 = 2,3 м.

R = 12 : 6,28 ≈ 1,9 м.

S = π · R · L = 3,14 * 1,9*2,3 = 13,7м²

Ответ: 13,7 м²

Задача на будущее (слайд 17) .

При взгляде на коническую кучу щебня или песка мне вспоминается старинная легенда восточных народов, рассказанная у А.С. Пушкина в "Скупом рыцаре". Послушайте её:

"Читал я где-то,

Что царь однажды воинам своим

Велел снести земли по горсти в кучу,-

И гордый холм возвысился,

И царь мог с высоты с весельем озирать

И дол, покрытый белыми шатрами,

И море, где бежали корабли".

• Какие ассоциации вызывают у Вас эти стихи? (Холм - конус).

• Какой высоты мог быть этот холм?

• Насколько километров может увеличиться панорама для наблюдения, поднявшегося с подножия холма к его вершине?

На все эти вопросы мы сможем ответить после изучения темы "Объем тел вращения". Это "задача на будущее".

VI. Итог урока.

Итак, мы повторили, как находить элементы конуса, площадь поверхности, применили свои знания в "геометрии на воздухе". Надеюсь, что в дальнейшем теоретические знания, полученные на уроках геометрии, вы сможете успешно использовать в разных жизненных ситуациях.

Рефлексия урока:

• Назовите 10 основных терминов, связанных с понятием « конус».

• Каков основной урок для вас лично?