Урок-конференция Теорема Пифагора

Урок конференция «Теорема Пифагора»

Адельберт Шамиссо о теореме Пифагора.

Суть истины вся в том, что нам она - навечно,

Когда хоть раз в прозрении её увидим свет,

И теорема Пифагора через столько лет

Для нас. Как для него, бесспорна, безупречна .

Цель урока :Обобщить и систематизировать знания учащихся по данной теме ;показать необходимость умения решать прямоугольные треугольники для разрешения практических проблем.

Задачи

• изучить историю открытия теоремы Пифагора;

• 
  
  исследовать различные методы доказательства данной теоремы,не рассматриваемые в школе;

• 
  
  выяснить практическую значимость теоремы.

Оборудование:

• доска

• магнитная доска.

• компьютер.

• мультимедийный комплекс

• плакаты с высказываниями Пифагора

Ход урока

1.Организационный момент ( тема урока ,цель.)

Класс поделен на группы :1. «Исследователи»

2. «Теоретики»

3. «Практики»

2. Проверка домашней работы :

1. осуществляется консультантами внутри группы

Фронтальный опрос ( в форме теста)

1.Для сторон какого треугольника не выполняется теорема Пифагора?

2. В прямоугольном треугольнике сумма квадратов катетов равна…:

-а) сумме катетов;

-б)сумме квадратов катетов;

-в)квадрату суммы катетов;

3.Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то эта сторона лежит против…:

-а) острого угла;

-б) тупого угла;

-в)прямого угла;

4.Квадрат катета равен разности квадратов гипотенузы и другого катета

в треугольнике с углами :

-а)45⁰ и 50⁰

-б)30⁰ и45⁰

-в)28⁰ и62⁰

5.Какой из треугольников с указанными сторонами прямоугольный:

-а) 12; 9; 15;

-б)13; 14; 15;

-в)2; 5; 4;

6.В прямоугольном треугольнике катет, лежащий против угла в 30⁰ , равен «m»

Тогда второй катет..

-а)2m -б) m -в) m

7.В равнобедренном прямоугольном треугольнике катет равен « p».

Тогда гипотенуза равна..

-а) 2p -б) p -в)

8) Стороны прямоугольника равны 5см. и 12см.

Диагональ прямоугольника равна…

9) Боковая сторона равнобедренного треугольника равна 10см.,

а основание 16 см..Тогда высота, проведенная к основанию, равна…

10) Гипотенуза в прямоугольном треугольнике равна «в» , тогда катет

прилежащий к углу 30⁰ равен…

3.Пленарное заседание конференции

Слово предоставляется группе « Исследователи»

1-й докладчик:

(Краткая биография Пифагора)

Кроме чисел 3,4,5 существует , как известно , бесчисленное множество чисел удовлетворяющих соотношению а² +в²=с² Они называются Пифагоровыми числами .Согласно теореме Пифагора эти числа могут служить длинами сторон прямоугольного треугольника: а,в- катеты с- гипотенуза. Ясно ,что если числа а, в, с- пифагорова тройка , то для любого натурального числа n

Числа nа, nв, n с - тоже пифагоровы числа.

Пифагоровы числа обладают рядом интересных особенностей

1. Один из « катетов» должен быть кратен трём

2. Один из « катетов» должен быть кратен четырём

3. Одно из пифагоровых чисел должно быть кратно пяти

.

2докладчик (Сообщение о древнем способе для проведения на местности перпендикулярных прямых.)

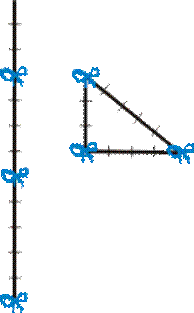
Слово предоставляется группе «Теоретики»

3 докладчик

Докажем теорему Пифагора , ( рассмотреть 2-3 способа)

.

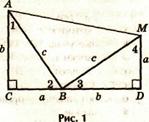
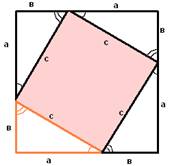Слово предоставляется группе «Практики»

4. Докладчик

Долгое время считали , что теорема Пифагора до Пифагора не была известна ,и поэтому она носит его имя. Однако в настоящее время установлено , эта важнейшая теорема встречается в Вавилонских текстах, написанных за 1200 лет до Пифагора.

Египтяне придумали задачу о лотосе

На глубине 12 футов растет лотос с тринадцати футовым стеблем

Определите , на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну.

Решение

d= =5

Ответ:5 футов

Заслугой, Пифагора, является не открытие теоремы Пифагора, ее доказательство."

5 докладчик

Задача индийского ученого Бхаскара Акариа, 1114 г.

На берегу ручья, ширина которого 4 фута, рос тополь. Порыв ветра сломил его на высоте в 3 фута от земли так, что верхний конец его коснулся другого берега ручья (ствол направлен перпендикулярно течению). Определить высоту тополя

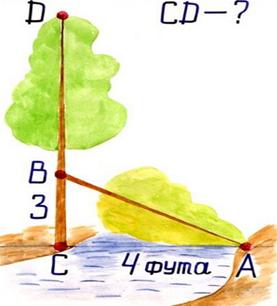
Задача из учебника «Арифметика» Леонтия Магницкого:

«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать».

Применение в мобильной связи

В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например радиусе R=200 км?, если известно. что радиус Земли равен 6380 км.)



Решение:

Пусть AB= x, BC=R=200 км, OC= r =6380 км.

OB = OA + AB

OB = r + x

Используя теорему Пифагора, получим ответ.

Ответ: 2,3 км.

Применение в строительстве , архитектуре , в астрономии( показ слайдов)

4.Мозговой штурм

Каждая группа получает карточку с задачами , которые нужно решить за10 минут:

Карточка

1.Бамбуковый ствол высотой 9 футов переломлен бурей так , что если верхнюю часть его пригнуть к земле , то верхушка уоснется земли на расстоянии 3 футов от основания ствола. На какой высоте переломлен ствол?

2.Эсколатор метрополитена имеет 17 ступенек от пола наземного вестибюля

До пола подземной станции. Ширина ступенек 40см. , высота 30см. Определите :а) длину лестницы; б) угол ее наклона; в)глубину станции по вертикали.

Защита работ( у доски)

Заключение

Изучив историю открытия теоремы Пифагора, выяснилось, что Пифагор открыл не саму теорему, а ее доказательство.



Исследовав различные методы доказательства теоремы Пифагора, оказалось, что таких доказательств огромное количество и разделить их можно на сл

Выяснив практическую значимость теоремы Пифагора, оказалось, что теорема имеет большое применение в повседневной жизни в разных сферах человеческой деятельности: астрономии, строительстве, мобильной связи, архитектуре

Рефлексия

Какую цель мы ставили перед собой ?

Как вы оцениваете свою работу ?

Что вам понравилось ?

Мне приятно было с вами работать!

Домашнее задание: Отыскать другие доказательства теоремы Пифагора

Литература.

1. Геометрия: учеб. для 7-9 кл. сред. шк. / авт.-сост. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. - 4-е изд. - М.: Просвещение, 2015. - 383 с

2. Энциклопедический словарь юного математика / сост. А. П. Савин. - М.: Педагогика, 1989. - 352 с.

3. .Глейзер Г. И. История математики в школе. М., 1982

4. .История теоремы Пифагора

5. .th-pif.narod.ru/pract.htm