Учитель математики

МБОУ г. Иркутска СОШ № 39

Бордачёва Ирина Викторовна

Урок математики в 5-м классе

Решение задач с помощью уравнений

(Организация групповой работы при решении задач)

Тема урока: решение задач с помощью уравнений.

Цели урока: формирование умений при решении задач на составление уравнений, закрепление действий с десятичными дробями;

повторение свойств действий над числами;

развитие навыков самоконтроля и взаимоконтроля;

развитие ассоциативной памяти, логического мышления;

развитие интереса к математике через исторические факты;

формирование умения работать в коллективе и самостоятельно.

Учебник: Виленкин Н. Я., Жохов В. И. и др.

План:

1. Организация начала урока. Постановка цели.

2. Актуализация опорных знаний. Фронтальный опрос по теме «Действия с десятичными дробями». Написание диктанта с последующей взаимопроверкой по теме «Упрощение выражений и буквенные выражения».

3. Исторические факты. Разбор решения задачи.

4. Физкультминутка и формулировка домашнего задания.

5. Решение задач: работа класса и групп.

6. Подведение итогов урока. Выставление оценок.

1 слайд. Вступительное слово учителя. Учитель разъясняет ребятам цели урока, сообщает о том, что на уроке они познакомятся с некоторыми историческими фактами.

2 слайд. Задание для устного счёта (повторение действий с десятичными дробями): вставьте пропущенное число.

4   = 4,8; 3   = 4,5;

  2 = 0,6; 10   = 6;

0,5 :  = 0,05; 5 :  = 2;

 : 0,5 = 8;  : 0,3 = 3.

Работа в тетрадях. Актуализация опорных знаний с помощью математического диктанта. Ребята записывают выражение и, если возможно, то упрощают его.

3-4 слайды. Диктант.

1. 3,6х + 2,4х;

2. 5,7у - у;

3. х + 1,5х;

4. У Маши х яблок, а у Пети в 2 раза больше.

а) Сколько яблок у Пети?

б) Сколько яблок у них вместе?

5. В одном кабинете у парт, а в другом на 4 парты больше.

а) Сколько парт в другом кабинете?

б) Сколько парт в двух кабинетах?

6. С одного дерева сняли а кг яблок, а с другого в 4 раза больше. На сколько килограммов яблок сняли больше со второго дерева, чем с первого?

5 слайд. После проведения диктанта взаимопроверка и выставление оценок.

Далее перед решением задач, ребята слушают историческую справку.

6-9 слайды. Историческая справка. Сегодня, ребята, мы с вами совершим небольшое путешествие в Московский Кремль. Столицу нашей родины г. Москва невозможно представить без её красивейшего Кремля. Все башни Кремля построены выше стен. Это позволяло в случае захвата неприятелем верхнего хода стены, вести обстрел сверху. Форма башен диктовалась местом их возведения и ролью в обороне. Угловые башни, предназначенные для кругового обстрела местности - круглые или многогранные, а остальные, из которых вели фронтальный и фланговый обстрел - четырёхгранными. Всего в Кремле 20 башен. Пожалуй, самая известная - Спасская, через ворота которой проезжает президентский кортеж, а наверху красуются главные часы нашей страны - куранты. Спасские ворота исстари были главными, парадными воротами Кремля. Возле них москвичи провожали воинов на битву, через них величественно проходили крестные ходы, триумфальные шествия. В особо торжественных случаях путь через ворота устилали дорогим красным сукном.

А знаете ли вы, что длина минутной стрелки курантов равна высоте двух человек среднего роста, если один встанет другому на плечи?

10 слайд. Часовая стрелка кремлёвских курантов на 0,31 м короче минутной. Вычислите длину стрелок, если известно, что они вместе имеют длину 6,25 м.

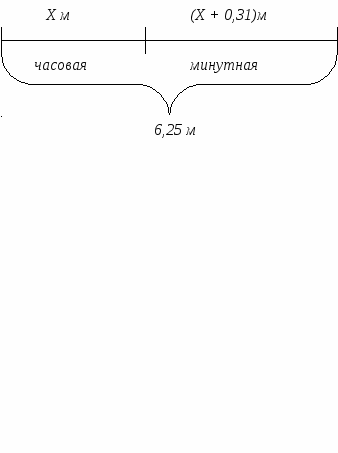
11 слайд. Схема:

12 слайд. Уравнение:

х + (х + 0,31) = 6,25

2х + 0,31 = 6,25

2х = 6,25 - 0,31

2х = 5,94

х = 5,94 : 2

х = 2,97

2,97 м - часовая стрелка

2,97 + 0,31 = 3,34(м) - минутная стрелка

Ученики должны заметить, что эту задачу также можно решить и арифметическим способом. Учитель акцентирует внимание на запись выражения в скобках и задаёт вопрос: обязательны ли скобки в данном конкретном случае.

13 слайд. Физкультминутка.

14 слайд. Формулировка домашнего задания: № 1490 (задача), № 1489(б) (уравнение) или на выбор № 1439(б, в) (упростить выражение).

Далее идёт работа в группах с более сложной задачей (2 группы более сильных ребят), а остальные ребята решают задачу попроще и самостоятельно.

Карточка. Задача для групп. Спасская башня Кремля состоит из башни, башенки и шатра. Какой высоты была Спасская башня Кремля в 1701 г., если известно, что высота башенки в 1,7 раза больше высоты шатра, а высота башни в 2,3 раза больше высоты шатра. Причём высота башни больше высоты башенки на 7,5 м.

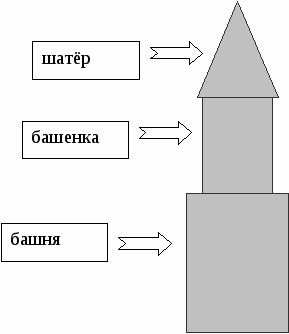
На 7,5 м

Х м

1,7Х м

2,3Х м

Схема:

шатёр

башенка

башня

Уравнение:

2,3х - 1,7х = 7,5

0,6х = 7,5

х = 7,5 : 0,6

х = 12,5

12,5 м - шатёр

1,7  12,5 = 21,25 (м) - башенка

2,3  12,5 = 28,75 (м) - башня

28,75 + 21,25 + 12,5 = 62,5 (м) - Спасская башня

Пока группы работают, класс в это время решает другую задачу. А предварительно историческая справка.

15 слайд. В Москве очень много церквей и соборов, на звонницах которых заливаются звоном колокола. А самый большой Царь-колокол продолжает лежать на месте, его вес более 6 тонн. После пожара 1733 года колокол треснул, и перелить его поручили юному литейному мастеру Александру Григорьеву. Из колоколов, им отлитых, следует упомянуть ещё два уникальных. Один из них принадлежал Симонову монастырю и имел самый красивый звон среди всех колоколов Москвы. Другой колокол был отлит для Саввино-Сторожевского монастыря в Звенигороде. Он считался самым благозвучным колоколом России. Колокол погиб во время Великой Отечественной войны.

16 слайд. Задача. Масса колокола Саввино-Сторожевского монастыря была в 2,4 раза больше массы колокола Симонова монастыря. Масса этих колоколов вместе составляет 55,08 т. Вычислите массу каждого колокола.

Задачу решает ученик у доски.

17 слайд. Схема:

Учитель ещё раз обращает внимание на правильную запись уравнения и его решение

18 слайд. Уравнение:

2,4х + х = 55,08

3,4х = 55,08

х = 55,08 : 3,4

х = 16,2

16,2 т - масса Симонова колокола

55,08 - 16,2 = 38,88 (т) - масса Саввино-Сторожевского колокола

После решения задач - подведение итогов урока и выставление оценок. Учитель просит ребят в тетрадях нарисовать 3 рефлексивных столбика: «мне было интересно», «мне было легко», «я работал на оценку…», максимальная высота столбика 5 клеток (по пятибалльной шкале). Учитель собирает тетради и позже делает анализ результатов.

Литература

1. Виленкин Н. Я., Жохов В. И. и др. Учебник для 5 класса общеобразовательных учреждений. - 24-е изд., испр. - М.: Мнемозина, 2008. - 280 с.

2. Перли С.С., Перли Б.С. Страницы русской истории на уроках математики: Нетрадиционный задачник. V - VI классы. - М.: Педагогика-Пресс, 1994. - 288 с.