- Учителю
- Урок по математике 'Решение простейших тригонометрических уравнений и неравенств' (10 класс)
Урок по математике 'Решение простейших тригонометрических уравнений и неравенств' (10 класс)


 МОУ «Соловьихинская средняя общеобразовательная школа»
МОУ «Соловьихинская средняя общеобразовательная школа»
Алгебра 10 класс
Учитель математики:
Шлыкова Л.А.
Цель урока: рассмотреть общий вид решений простейших тригонометрических уравнений.
Ход урока:
-
Орг. момент
Тема и цель урока
-
Повторение и закрепление пройденного материала.
-
Разбор дом. задания и решение нерешенных заданий
-
Контроль усвоения материала (самостоятельная работа)
____________________________________________________________________
Вариант 1.
-
Дать определение и перечислить свойства арксинуса.
-
Вычислить:
а) arcsin( - 1) + arcsin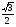 ; б) arccos
; б) arccos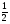 + arcsin
+ arcsin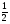 ;
;
в) arctg( - 1) - arccos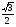 ; г) cos(arccos
; г) cos(arccos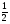 + arccos
+ arccos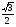 ).
).
________________________________________________________________________
Вариант - 2.
-
Дать определение и перечислить свойства арккосинуса.
-
Вычислить:
а) arcsin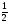 - arcsin 1; б) arcos ( - 1) + arctg
- arcsin 1; б) arcos ( - 1) + arctg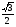 ;
;
в) arcsin 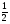 + arcsin( -
+ arcsin( - 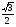 ); г) sin(arccos
); г) sin(arccos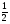 + arcsin
+ arcsin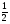 )
)
-
Изучение нового материала (лекция с применением м/м)
Для решения любого тригонометрического уравнения его надо свести к одному из четырех простейших. Простейшими тригонометрическими уравнениями являются cos x = a, sin x = a, tg x = a,ctg x = a. Рассмотрим их решения.
cos x = a
x = ± arccos a + 2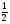 n, где n
n, где n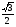 Z.
Z.
Функция соs х принимает значения из промежутка 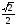 . Количество решений уравнения соs х =а зависит от значения числа а. Если а
. Количество решений уравнения соs х =а зависит от значения числа а. Если а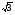
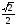 , то уравнение не имеет решений.
, то уравнение не имеет решений.
Если а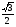
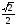 , на промежутке
, на промежутке 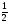 функция соs х убывает и принимает все значения от - 1 до 1. Поэтому по теореме о корне на этом промежутке уравнение соs х = а имеет единственное решение х1 = arccos a. Так как функция соs х четная, то на отрезке
функция соs х убывает и принимает все значения от - 1 до 1. Поэтому по теореме о корне на этом промежутке уравнение соs х = а имеет единственное решение х1 = arccos a. Так как функция соs х четная, то на отрезке 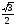
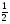 данное уравнение также имеет единственное решение х2 = - х1 = - arccos a. Итак, уравнение
данное уравнение также имеет единственное решение х2 = - х1 = - arccos a. Итак, уравнение
cos x = a на промежутке 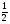 имеет два решения
имеет два решения
x = ± arccos a. Учитывая, что период косинуса равен 2π, то получаем формулу для записи всех решений данного уравнения:
x = ± arccos a + 2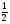 n, где n
n, где n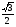 Z.
Z.
в частных случаях а = ± 1; а = 0 проще и удобнее использовать не общую формулу, а записывать решения на основании единичной окружности: cos x = 1, x = 2πk;
cos x = - 1, x = π + 2πk;
cos x = 0, x =  + πk, k
+ πk, k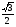 Z
Z
Например: решим уравнение cos х = - 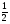 .
.
Используя приведенную формулу, запишем
x = ± arccos ( - 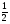 ) + 2
) + 2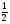 n, где n
n, где n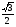 Z.
Z.
x = ±  + 2
+ 2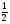 n, где n
n, где n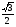 Z.
Z.
sin x = a
x = ( - 1)karcsin a + 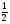 k, где k
k, где k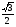 Z.
Z.
очевидно, что при а >1 такое уравнение решений не имеет, так как функция синус ограничена и 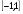 ≤ 1. На отрезке
≤ 1. На отрезке 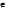 функция sin x возрастает и принимает все значения от - 1 до 1. Тогда по теореме о корне на этом промежутке при
функция sin x возрастает и принимает все значения от - 1 до 1. Тогда по теореме о корне на этом промежутке при 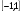 ≤1 уравнение sin x = а имеет единственное решение х1 = arcsin a. На отрезке
≤1 уравнение sin x = а имеет единственное решение х1 = arcsin a. На отрезке  функция sin x убывает и также принимает все значения от - 1 до 1. Поэтому и на этом промежутке при
функция sin x убывает и также принимает все значения от - 1 до 1. Поэтому и на этом промежутке при 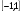 ≤1 уравнение sin x = а тоже имеет единственное решение х2 = - х1 = - arcsin a. Действительно, sin x2 = sin( - x1) = sin x1 = a. Кроме того, поскольку
≤1 уравнение sin x = а тоже имеет единственное решение х2 = - х1 = - arcsin a. Действительно, sin x2 = sin( - x1) = sin x1 = a. Кроме того, поскольку 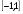 , то есть х2 принадлежит отрезку
, то есть х2 принадлежит отрезку  .
.
Учитывая, что период синуса равен 2, получаем две формулы для записи всех решений данного уравнения х = arcsin a + 2n и
x = - arcsin a + 2n, где nєZ. Такие решения удобно описывать не двумя, а одной формулой :
x = ( - 1)karcsin a + 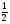 k, где k
k, где k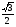 Z.
Z.
действительно, при четных k = 2n из этой формулы получаем все решения, описываемые первой формулой; при нечетных k = 2n + 1 - решения, записываемые второй формулой.
Заметим, что в частных случаях а=0; ± 1 проще и удобнее использовать не общую формулу, а записывать решения на основании единичной окружности:
Для уравнения sin x = 1 решения x = 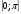
Для уравнения sin x = 0 решения 
Для уравнения sin x = - 1 решения x = 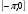 , kєZ
, kєZ
Пример 2:
Решим уравнение 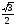 sin x =
sin x = 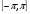 .
.
По приведенной формуле запишем решения уравнения
x = ( - 1)karcsin (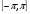 ) + k, kєZ
) + k, kєZ
x = ( - 1)k + k, kєZ
+ k, kєZ
x = ( - 1)k+1 + k, kєZ
+ k, kєZ
tg x = a
x = arctg a + k, kєZ
на отрезке  функция tg x возрастает и принимает все значения от - ∞ до ∞. Тогда по теореме о корне при любом значении а на этом промежутке уравнение tg x = а имеет единственное решение, равное х = arctg a. Так как функция тангенс имеет период , то получаем формулу для всех решений данного уравнения:
функция tg x возрастает и принимает все значения от - ∞ до ∞. Тогда по теореме о корне при любом значении а на этом промежутке уравнение tg x = а имеет единственное решение, равное х = arctg a. Так как функция тангенс имеет период , то получаем формулу для всех решений данного уравнения:
x = arctg a + k, kєZ
Пример 3. Решим уравнение 3 tg x = 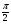
Запишем уравнение в виде tg x =  или tg x =
или tg x = 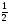 . Используя приведенную формулу, выпишем решения уравнения
. Используя приведенную формулу, выпишем решения уравнения
х = arctg 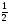 + k, kєZ
+ k, kєZ
x = 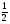 + k, kєZ
+ k, kєZ
-
Закрепление
№№ 136(а,г) 137(в) 139(б) 140(а) 145 (а,б)
-
Контрольные вопросы:
Выпишите решения простейших тригонометрических уравнений.
-
Домашнее задание:
№№ 136(в) 137(г) 139(в) 141(г) 146(а)
-
Творческое задание
sin (2x +  ) =
) =  ; cos (3x -
; cos (3x - 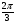 ) =
) =  .
.
____________________________________________________________________
Вариант 1.
-
Дать определение и перечислить свойства арксинуса.
-
Вычислить:
а) arcsin( - 1) + arcsin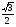 ; б) arccos
; б) arccos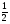 + arcsin
+ arcsin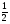 ;
;
в) arctg( - 1) - arccos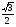 ; г) cos(arccos
; г) cos(arccos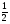 + arccos
+ arccos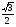 ).
).
________________________________________________________________________
Вариант - 2.
-
Дать определение и перечислить свойства арккосинуса.
-
Вычислить:
а) arcsin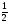 - arcsin 1; б) arcos ( - 1) + arctg
- arcsin 1; б) arcos ( - 1) + arctg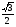 ;
;
в) arcsin 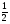 + arcsin( -
+ arcsin( - 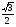 ); г) sin(arccos
); г) sin(arccos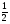 + arcsin
+ arcsin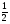 )
)
________________________________________________________________________