Конспект урока по математике в 6 классе по теме 'Числовые промежутки'.

Тема: Числовые промежутки.

Цель: К концу урока учащиеся знают различные виды числовых промежутков, умеют изображать значения числовых неравенств на числовой прямой. Знают понятия пересечения и объединения числовых промежутков. Формируют навыки сравнения и анализа, применяя полученные знания при решении упражнений.

Развивают аккуратность, память, речь, внимание, логическое мышление.

Воспитывают ответственность, упорство и волю для достижения конечных результатов, настойчивость в учении.

Ход урока.

1. Организационный момент.

2. Проверка домашнего задания предполагает взаимную проверку по образцу.

3. Разминка. Вычислить: (-4) *(-12); 17*(-2); (-3) *(-7); 8*(-7); (-20) *(-5); (-15) *3; (-4) :(-5); -16:(-5); 24:(-3); -5, 1:3; -1, 6:0,1; -30:0,5.

Какие правила применялись при вычислении примеров?

4. Фронтальный опрос.

1. Какие свойства числовых неравенств используются в следующих неравенствах? 1) 5>3, то 3<5;

2) 9,2>5,2 и 5,2>4,8, то 9,2>4,8;

3) 0,5> -3, тогда 0,5+2> -3+2;

4) 4,5<12, тогда 4,5*2<12*2 и 4, 5:3<12:3;

5) 5,5>3,3, тогда 5,5:(-1,1) <3,3:(-1,1) и 5,5*(-1) <3,3*(-1);

6) 15>5, тогда 1/15<1/5

Учащиеся определяют свойства числовых неравенств по приведенным примерам.

2. С какими действиями над числовыми неравенствами вы ещё знакомы? (предполагаемый ответ: сложение и вычитание, а также умножение и деление числовых неравенств).

Как найти произведение двух неравенств с разными знаками неравенства?

(ответ: применяем 1-е свойство и правило умножения неравенств).

Как найти частное неравенств одного разных знаков, одного знака?

Найдите произведение и частное: 0,4>0,2 и 5>0,5; 3,5 <1,2 и 4> 0,3.

5. Изложение нового материала проводится совместно в диалоге с учащимися.

В ходе совместного прочтения параграфа по частям заполняем таблицу.

Неравенство

Изображение на координатной прямой

Название промежутка

Запись неравенства в виде промежутка

-2<������

�����������

�������

�����

����������

��

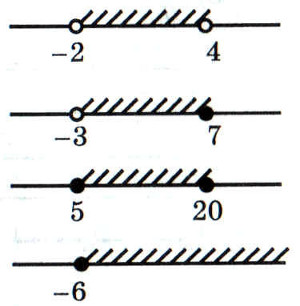
5≤х≤20

отрезок

[5;20]

х≥-6

Луч или открытый луч

[-6;∞)

Два числовых промежутка между собой могут «пересекаться», «объединятся» или их пересечение может быть «пустым» множеством.

[ - 2; 4] ∩ [ 1; 6 ] = [ 1; 4]

[ -4; 1] ∩ [ 3;7] = Ø; [ -4; 1] ∩ [ 3;7] =Ø.

6. По завершению разбора нового материала, предлагается ряд вопросов, отвечая на которые еще раз обобщается изученный материал. Во время обобщения, в случае затруднения, можно пользоваться учебником.

1. Что наз. числовым промежутком?

2. Какие виды промежутков существуют?

3. Какие знаки называются строгими и нестрогими?

4. Если неравенства записываются строгими знаками, то какие скобки используются при записи промежутков.

5. Если неравенства записываются нестрогими знаками ≤ или ≥, то какие скобки используются при записи промежутков.

6. Когда нужно использовать вместе круглые и квадратные скобки для обозначения числовых промежутков?

7. Как называется решение неравенства, лежащими между точками с заданными координатами (не включая данные точки)?

8. Какой числовой промежуток называется отрезком?

7. С целью выяснения усвоения данной темы предлагается самостоятельная работа на два варианта.

1. Выпишите целые числа, принадлежащие промежутку:

а) [ -5; 2 ] б) (-6; 4) а) [ -7; 6) б) (-3; 4]

2. Запишите с помощью числовых промежутков следующие выражения:

а) отрезок от 3 до 7 а) отрезок от -5 до 4

б) интервал от -2 до 4 б) интервал от -4 до 0

в) полуинтервал от 3 до 7, включая 7 в) полуинтервал от 0 до 3, включая 0

г) луч от -∞ до 15 г) открытый луч от 6 до ∞.

1. Запишите неравенство в виде промежутка:

-4<�������

��≤8 -6≤х<8

2≤х≤13 5≤х≤13

х≥-5 х≤4

х≤∞ х≥∞

Самопроверка по образцу.

8. Домашнее задание: Параграф - 5.6, составить кроссворд используя терминологию неравенств (не менее семи слов). № 987, № 988, № 989.

9. Рефлексия. Прием «Комплимент».

Для того чтобы закончить урок на положительной ноте можно воспользоваться одним из вариантов упражнении «Комплимент» (комплимент-похвала, комплимент деловым качествам, комплимент в чувствах), в котором учащиеся оценивают вклад друг друга в урок и благодарят друг друга и учителя за проведенный урок. Такой вариант окончания урока дает возможность удовлетворения потребности в признании личностной значимости каждого.

10. Итог урока.